3.1.2弧度制_课件1-湘教版必修2(24张PPT)
文档属性
| 名称 | 3.1.2弧度制_课件1-湘教版必修2(24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览







文档简介
1.理解弧度制的意义,能正确进行弧度与角度的换算.
2.理解弧度制下,任意角的集合与实数集之间建立一一
对应的关系.
3.掌握扇形的弧长公式及扇形的面积公式.
弧度制
角的单位制
(1)角度制:规定周角的 为1度的角,用度作为单位来度量角的单位制叫做角度制.
(2)弧度制:单位圆上长度为1的圆弧所对的圆心角取为度量的单位,称作弧度(radian),这样的单位制称为弧度制(radian measure).
自学导引
1.
(3)角的弧度数求法:如果半径为r的圆的圆心角α=x弧度所对的弧长为l,那么l,x,r之间存在的关系是: ;
这里x的正负由角α的__________________决定.正角的弧
度数是一个____,负角的弧度数是一个____,零角的弧度数是__.
角度与弧度的互化
(1)周角=360°=2π弧度;
_______ 弧度,
终边的旋转方向
正数
负数
0
2.
0.017 45
1
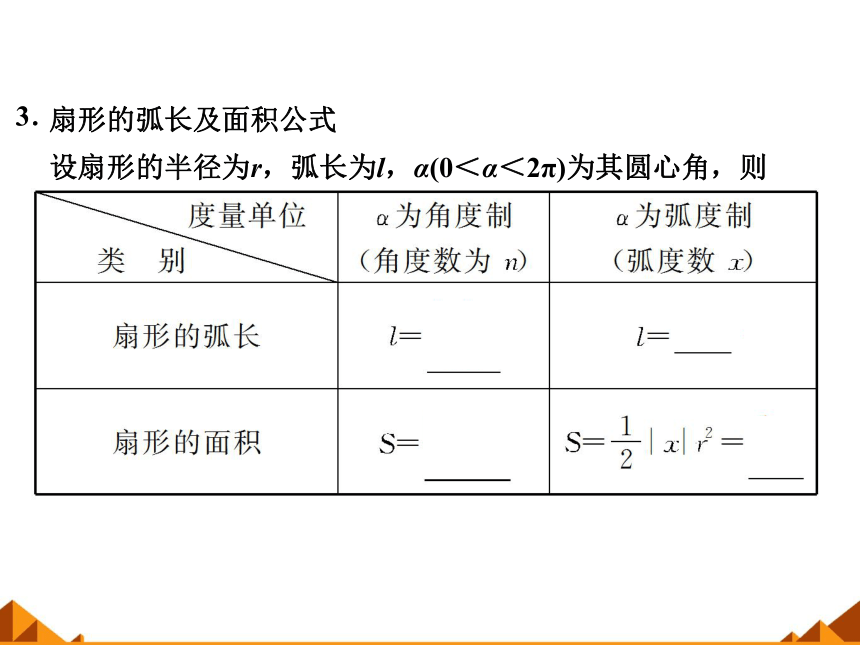
扇形的弧长及面积公式
设扇形的半径为r,弧长为l,α(0<α<2π)为其圆心角,则
3.
自主探究
下列叙述中,正确的是 ( ).
A.1弧度是1度的圆心角所对的弧
B.1弧度是长度为半径的弧
C.1弧度是1度的弧与1度的角之和
D.1弧度是长度等于半径长的弧所对的圆心角,它是角
的一种度量单位
答案 D
预习测评
1.
一条弦长等于圆的半径,则这条弦所对的圆心角的弧度数是 ( ).
2.
答案 A
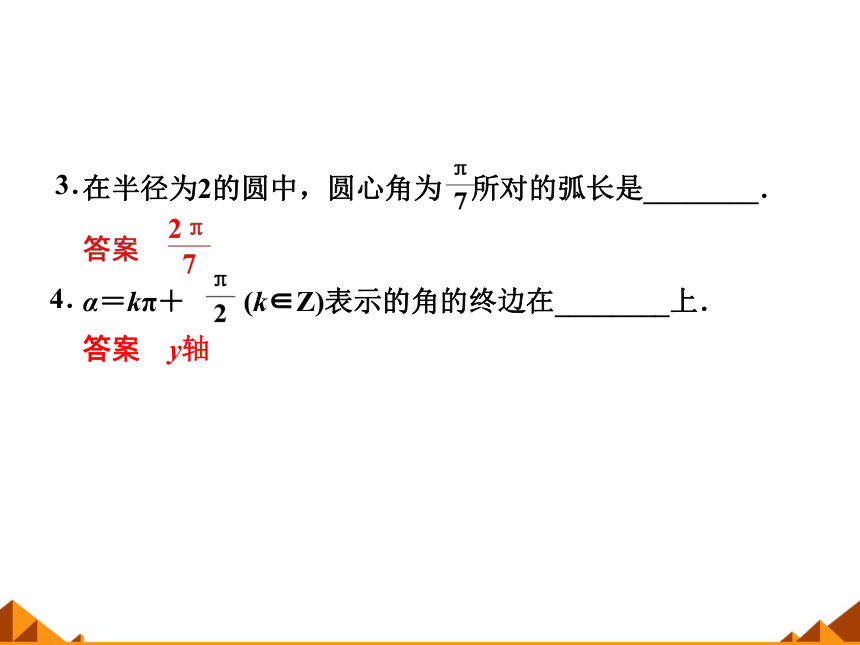
在半径为2的圆中,圆心角为 所对的弧长是________.
3.
α=kπ+ (k∈Z)表示的角的终边在________上.
答案 y轴
4.
弧度制的有关概念
关于弧度制的理解,主要明确如下几点:
名师点睛
1.
(3)无论是以“弧度”还是以“度”为单位,角的大小都是一个与“半径”大小无关的定值,“弧度”或“度”仅仅是为了能使角的概念描述得更具体而设置的一个“过渡量”,这对于推广角的概念有积极的意义.
角度制与弧度制的区别与联系
(1)用弧度为单位表示角的大小时,“弧度”两字可以省略不写,这时弧度数在形式上虽是一个不名数,但我们应当把它理解为名数,如sin2是指sin(2弧度),π=180°是指π弧度=180°;但如果以度“°”为单位表示角时,度“°”就不能省去.
2.
(2)弧度制和角度制一样,只是一种度量角的方法.弧度制与角度制相比有一定的优点.其一是在进位上,角度制在度、分、秒上是60进位制,不便于计算,而弧度制是十进位制,给运算带来方便;其二是在弧长公式与扇形面积公式的表达上,弧度制下的公式远比角度制下的公式简单,运用起来方便.
(3)需注意的一个问题,在今后表示角的时候,由于弧度制的优点,常常使用弧度制表示角,但也要注意,用弧度制表示角时,不能与角度制混用,例如:α=2kπ+30°
(k∈Z),β=k·360°+ π(k∈Z)都是不允许的.
(1)将下列各角度化成弧度:①1 080°;②-750°;
(2)将下列各弧度化成角度:①- ;② .
题型一 角度制与弧度制的换算
【例1】
典例剖析
1.
用弧度制表示顶点在原点,始边重合于x轴的非负半轴,终边落在阴影部分内的角的集合(不包括边界,如图)
题型二 弧度制表示角的范围
【例2】
点评 首先可以利用弧度制与角度制间的关系将有关角化为弧度数,同时在表示所给角的范围时还要注意正角和负角之间的转化.
用弧度制表示第二象限角的集合为________.
2.
解答下列各题:
(1)已知扇形的周长为10 cm,面积为4 cm2,求扇形圆心角的弧度数;
(2)已知一扇形的周长为40 cm,当它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?
解 (1)设扇形圆心角的弧度数为θ(0<θ<2π),弧长为l,半径为r,
题型三 扇形的弧长与面积
【例3】
①代入②得r2-5r+4=0,解之得r1=1,r2=4.
当r=1时,l=8 cm,此时,θ=8>2π舍去.
(2)设扇形的圆心角为x,半径为r,弧长为l,面积为S,则l+2r=40,
∴l=40-2r,
已知扇形OAB的圆心角α为120°,半径为6,求扇形弧长及所含弓形的面积.
3.
将-1 485°化成2kπ+α(0≤α<2π,k∈Z)的形式为________.
错解 因为-1 485°=-4×360°-45°
=-4×360°+(-360°+315°)=-5×360°+315°,
所以-1 485°化为2kπ+α形式应为-10π+315°
答案 -10π+315°
错因分析 只考虑了将-1 485°写成了“2kπ”的组合形式,而忽视了对α的要求,忽视了角度和弧度的统一,这是初学者易犯的一个错误.
误区警示 因角度制与弧度制混用而出错
【示例】
正解 由-1 485°=-5×360°+315°,
纠错心得 表示角时,要么全用角度制,要么全用弧度制,不能混用.
角度制与弧度制的互化:熟记基本关系180°=π弧度.然后用公式 进行求解,并注意各自的单位.
角进行了推广后,实数与角之间建立了一种一一对应关系,即每一个角都有唯一的实数与它对应,反过来,每一个实数也都有唯一的一个角与它对应.
使用弧度制下的弧长公式,扇形面积公式有诸多优越性,但是如果已知角是以“度”为单位,则必须先把它化成弧度后再计算.
课堂总结
1.
2.
3.
2.理解弧度制下,任意角的集合与实数集之间建立一一
对应的关系.
3.掌握扇形的弧长公式及扇形的面积公式.
弧度制
角的单位制
(1)角度制:规定周角的 为1度的角,用度作为单位来度量角的单位制叫做角度制.
(2)弧度制:单位圆上长度为1的圆弧所对的圆心角取为度量的单位,称作弧度(radian),这样的单位制称为弧度制(radian measure).
自学导引
1.
(3)角的弧度数求法:如果半径为r的圆的圆心角α=x弧度所对的弧长为l,那么l,x,r之间存在的关系是: ;
这里x的正负由角α的__________________决定.正角的弧
度数是一个____,负角的弧度数是一个____,零角的弧度数是__.
角度与弧度的互化
(1)周角=360°=2π弧度;
_______ 弧度,
终边的旋转方向
正数
负数
0
2.
0.017 45
1
扇形的弧长及面积公式
设扇形的半径为r,弧长为l,α(0<α<2π)为其圆心角,则
3.
自主探究
下列叙述中,正确的是 ( ).
A.1弧度是1度的圆心角所对的弧
B.1弧度是长度为半径的弧
C.1弧度是1度的弧与1度的角之和
D.1弧度是长度等于半径长的弧所对的圆心角,它是角
的一种度量单位
答案 D
预习测评
1.
一条弦长等于圆的半径,则这条弦所对的圆心角的弧度数是 ( ).
2.
答案 A
在半径为2的圆中,圆心角为 所对的弧长是________.
3.
α=kπ+ (k∈Z)表示的角的终边在________上.
答案 y轴
4.
弧度制的有关概念
关于弧度制的理解,主要明确如下几点:
名师点睛
1.
(3)无论是以“弧度”还是以“度”为单位,角的大小都是一个与“半径”大小无关的定值,“弧度”或“度”仅仅是为了能使角的概念描述得更具体而设置的一个“过渡量”,这对于推广角的概念有积极的意义.
角度制与弧度制的区别与联系
(1)用弧度为单位表示角的大小时,“弧度”两字可以省略不写,这时弧度数在形式上虽是一个不名数,但我们应当把它理解为名数,如sin2是指sin(2弧度),π=180°是指π弧度=180°;但如果以度“°”为单位表示角时,度“°”就不能省去.
2.
(2)弧度制和角度制一样,只是一种度量角的方法.弧度制与角度制相比有一定的优点.其一是在进位上,角度制在度、分、秒上是60进位制,不便于计算,而弧度制是十进位制,给运算带来方便;其二是在弧长公式与扇形面积公式的表达上,弧度制下的公式远比角度制下的公式简单,运用起来方便.
(3)需注意的一个问题,在今后表示角的时候,由于弧度制的优点,常常使用弧度制表示角,但也要注意,用弧度制表示角时,不能与角度制混用,例如:α=2kπ+30°
(k∈Z),β=k·360°+ π(k∈Z)都是不允许的.
(1)将下列各角度化成弧度:①1 080°;②-750°;
(2)将下列各弧度化成角度:①- ;② .
题型一 角度制与弧度制的换算
【例1】
典例剖析
1.
用弧度制表示顶点在原点,始边重合于x轴的非负半轴,终边落在阴影部分内的角的集合(不包括边界,如图)
题型二 弧度制表示角的范围
【例2】
点评 首先可以利用弧度制与角度制间的关系将有关角化为弧度数,同时在表示所给角的范围时还要注意正角和负角之间的转化.
用弧度制表示第二象限角的集合为________.
2.
解答下列各题:
(1)已知扇形的周长为10 cm,面积为4 cm2,求扇形圆心角的弧度数;
(2)已知一扇形的周长为40 cm,当它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?
解 (1)设扇形圆心角的弧度数为θ(0<θ<2π),弧长为l,半径为r,
题型三 扇形的弧长与面积
【例3】
①代入②得r2-5r+4=0,解之得r1=1,r2=4.
当r=1时,l=8 cm,此时,θ=8>2π舍去.
(2)设扇形的圆心角为x,半径为r,弧长为l,面积为S,则l+2r=40,
∴l=40-2r,
已知扇形OAB的圆心角α为120°,半径为6,求扇形弧长及所含弓形的面积.
3.
将-1 485°化成2kπ+α(0≤α<2π,k∈Z)的形式为________.
错解 因为-1 485°=-4×360°-45°
=-4×360°+(-360°+315°)=-5×360°+315°,
所以-1 485°化为2kπ+α形式应为-10π+315°
答案 -10π+315°
错因分析 只考虑了将-1 485°写成了“2kπ”的组合形式,而忽视了对α的要求,忽视了角度和弧度的统一,这是初学者易犯的一个错误.
误区警示 因角度制与弧度制混用而出错
【示例】
正解 由-1 485°=-5×360°+315°,
纠错心得 表示角时,要么全用角度制,要么全用弧度制,不能混用.
角度制与弧度制的互化:熟记基本关系180°=π弧度.然后用公式 进行求解,并注意各自的单位.
角进行了推广后,实数与角之间建立了一种一一对应关系,即每一个角都有唯一的实数与它对应,反过来,每一个实数也都有唯一的一个角与它对应.
使用弧度制下的弧长公式,扇形面积公式有诸多优越性,但是如果已知角是以“度”为单位,则必须先把它化成弧度后再计算.
课堂总结
1.
2.
3.
