3.2.2同角三角函数之间的关系_课件1(1)-湘教版必修2(28张PPT)
文档属性
| 名称 | 3.2.2同角三角函数之间的关系_课件1(1)-湘教版必修2(28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览








文档简介
1.掌握同角三角函数的基本关系式的推导方法.
2.会用同角三角函数的基本关系式化简三角函数式、求任意
角的三角函数值,证明简单的三角恒等式.
3.通过同角三角函数的基本关系式的推导进一步理解三角函
数的定义,体会数形结合思想.通过同角三角函数的基本
关系的应用,感受转化与化归思想在三角函数中的作用.
同角三角函数之间的关系
同角三角函数的基本关系式
(1)__________________.
自学导引
1.
sin2α+cos2α=1
(2)
.
基本关系式的常用变形
(1)sin2α=____________;cos2α=___________;
(2)(sin α+cos α)2=_________________;
2.
1-cos2α
1-sin2α
1+2sin αcos α
(3)(sin α-cos α)2=________________;
(4)(sin α+cos α)2+(sin α-cos α)2=______;
(5)sin α=______________;
(6)cos α=
1-2sin αcos α
2
cos αtan α
.
自主探究
若sin α= 且α为第一象限角,则tan α的值是 ( ).
预习测评
1.
答案 D
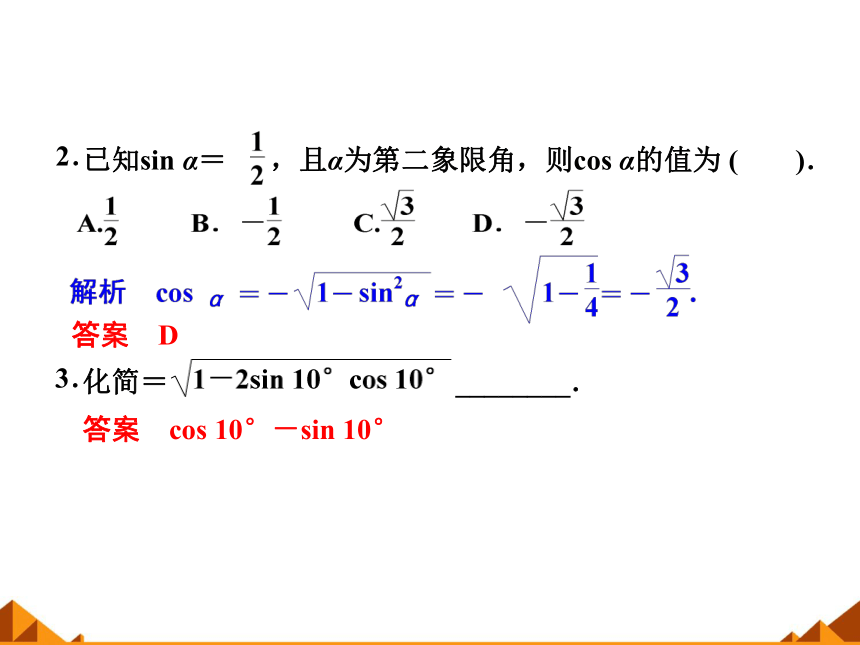
已知sin α= ,且α为第二象限角,则cos α的值为 ( ).
2.
答案 D
化简= ________.
答案 cos 10°-sin 10°
3.
若θ是△ABC的内角,且sin θ·cos θ=- ,则sin θ-cos θ
的值为________.
4.
对基本关系式的理解
(1)注意“同角”,这里“同角”有两层含义:一是“角相同”,二是对“任意”一个角(在使函数有意义的前提下)关系式都成立,与角的表达形式无关.如:sin23α+cos23α=1;
名师点睛
1.
(3)公式的应用非常广泛,除记住公式的原型外,还应注意公式的逆用和变形.
三个基本思想方法
(1)“1”的代换.为了解题的需要有时可以将1用“sin2α+cos2α”代替.
(2)切化弦.利用商数关系把正切化为正弦和余弦函数.
(3)整体代替.将计算式适当变形使条件可以整体代入或将条件适当变形找出与算式之间的关系.
2.
化简或证明应注意的问题
(1)化简是一种不指定答案的恒等变形,化简结果尽可能使项数少,函数的种类少、次数低,能求出值的要求出值,无根式、无分式等.
(2)证明简单的三角函数关系式常用的途径有:①由左边推至右边,或由右边推至左边,遵循的是化繁为简的原则;②两边夹法,即左边=A,右边=A,则左边=右边,这里的A起着桥梁的作用;③左边-右边=0,或
=1,通过作差或作商,将原式转化为一个等价的、更便于证明的等式.
3.
(3)在计算、化简或证明三角函数式时,常用的技巧有:减少不同名的三角函数,或化切为弦,或化弦为切;多项式运算技巧的运用,如因式分解等;条件或结论的重新整理、配置和改造,以便更有利于同角三角函数式的应用.
(4)运用三个基本关系式进行化简、求值、证明时,主要是灵活运用公式,消除差异,其思维模式归纳为三点:
①发现差异:观察角、函数、关系结构的差异;
②寻求联系:运用相关公式,找出转化差异的联系;
③合理转化:选择恰当的公式,实现差异的转化.
在解决问题的过程中,要注意运用方程的思想、等价转化的思想和分类讨论的思想等.
题型一 已知某一个三角函数值,求同角的其余三角函数值
【例1】
典例剖析
点评 同角三角函数的基本关系式揭示了同角之间的三角函数关系,其最基本的应用是“知一求二”,要注意这个角所在的象限,由此来决定所求是一解还是两解,同时应体会方程思想的应用.
1.
题型二 化简与证明
【例2】
点评 解答此类题目的关键在于公式的灵活运用,切实分析好同角三角函数间的关系.化简过程中常用的方法有:(1)化切为弦,即把非正弦、非余弦的函数都化成正弦、余弦函数,从而减少函数名称,达到化简的目的.(2)对于含有根号的,常把根号下化成完全平方式,然后去根号,达到化简的目的.特别需要注意的是去根号时的正负问题.(3)对于化简含高次的三角函数式,往往借助于因式分解.(4)化简结果的一般要求:①函数种类最少;②项数最少;③函数次数最低;④能求值的求出值;⑤尽量使分母不含三角函数;⑥尽量使分母不含根式.
2.
已知tan α=3,求下列各式的值:
题型三 已知α的正切值的求值问题
【例3】
点评 将所求三角函数式通过恒等变形,用已知三角函数表示出来,是一种整体思想,利用“1=sin2α+cos2α”将常数转化为三角函数,是一种重要的三角变换技巧,须切实领会和掌握,本例中,若由tan α=3分别求出sin α和cos α的值,则需讨论α是第一还是第三象限角,这无疑会增加计算量,走许多弯路.
已知tan α=2,求下列各式的值:
3.
已知sin α=m,|m|≤1,试用m表示cos α与tan α.
误区警示 因未按角α所在的象限分类讨论而出错
【示例】
纠错心得 当角α的某个三角函数的值含有字母,则应按字母的取值确定角α所在的象限,然后才好用这个字母表示角α的其它三角函数值.
根据同角三角函数的基本关系式,如果知道一个角的某一个三角函数值,可以求出这个角的其它两个三角函数值.在利用平方关系进行开方时,一定要注意判定角的范围,从而确定正确的符号.
课堂总结
1.
2.
2.会用同角三角函数的基本关系式化简三角函数式、求任意
角的三角函数值,证明简单的三角恒等式.
3.通过同角三角函数的基本关系式的推导进一步理解三角函
数的定义,体会数形结合思想.通过同角三角函数的基本
关系的应用,感受转化与化归思想在三角函数中的作用.
同角三角函数之间的关系
同角三角函数的基本关系式
(1)__________________.
自学导引
1.
sin2α+cos2α=1
(2)
.
基本关系式的常用变形
(1)sin2α=____________;cos2α=___________;
(2)(sin α+cos α)2=_________________;
2.
1-cos2α
1-sin2α
1+2sin αcos α
(3)(sin α-cos α)2=________________;
(4)(sin α+cos α)2+(sin α-cos α)2=______;
(5)sin α=______________;
(6)cos α=
1-2sin αcos α
2
cos αtan α
.
自主探究
若sin α= 且α为第一象限角,则tan α的值是 ( ).
预习测评
1.
答案 D
已知sin α= ,且α为第二象限角,则cos α的值为 ( ).
2.
答案 D
化简= ________.
答案 cos 10°-sin 10°
3.
若θ是△ABC的内角,且sin θ·cos θ=- ,则sin θ-cos θ
的值为________.
4.
对基本关系式的理解
(1)注意“同角”,这里“同角”有两层含义:一是“角相同”,二是对“任意”一个角(在使函数有意义的前提下)关系式都成立,与角的表达形式无关.如:sin23α+cos23α=1;
名师点睛
1.
(3)公式的应用非常广泛,除记住公式的原型外,还应注意公式的逆用和变形.
三个基本思想方法
(1)“1”的代换.为了解题的需要有时可以将1用“sin2α+cos2α”代替.
(2)切化弦.利用商数关系把正切化为正弦和余弦函数.
(3)整体代替.将计算式适当变形使条件可以整体代入或将条件适当变形找出与算式之间的关系.
2.
化简或证明应注意的问题
(1)化简是一种不指定答案的恒等变形,化简结果尽可能使项数少,函数的种类少、次数低,能求出值的要求出值,无根式、无分式等.
(2)证明简单的三角函数关系式常用的途径有:①由左边推至右边,或由右边推至左边,遵循的是化繁为简的原则;②两边夹法,即左边=A,右边=A,则左边=右边,这里的A起着桥梁的作用;③左边-右边=0,或
=1,通过作差或作商,将原式转化为一个等价的、更便于证明的等式.
3.
(3)在计算、化简或证明三角函数式时,常用的技巧有:减少不同名的三角函数,或化切为弦,或化弦为切;多项式运算技巧的运用,如因式分解等;条件或结论的重新整理、配置和改造,以便更有利于同角三角函数式的应用.
(4)运用三个基本关系式进行化简、求值、证明时,主要是灵活运用公式,消除差异,其思维模式归纳为三点:
①发现差异:观察角、函数、关系结构的差异;
②寻求联系:运用相关公式,找出转化差异的联系;
③合理转化:选择恰当的公式,实现差异的转化.
在解决问题的过程中,要注意运用方程的思想、等价转化的思想和分类讨论的思想等.
题型一 已知某一个三角函数值,求同角的其余三角函数值
【例1】
典例剖析
点评 同角三角函数的基本关系式揭示了同角之间的三角函数关系,其最基本的应用是“知一求二”,要注意这个角所在的象限,由此来决定所求是一解还是两解,同时应体会方程思想的应用.
1.
题型二 化简与证明
【例2】
点评 解答此类题目的关键在于公式的灵活运用,切实分析好同角三角函数间的关系.化简过程中常用的方法有:(1)化切为弦,即把非正弦、非余弦的函数都化成正弦、余弦函数,从而减少函数名称,达到化简的目的.(2)对于含有根号的,常把根号下化成完全平方式,然后去根号,达到化简的目的.特别需要注意的是去根号时的正负问题.(3)对于化简含高次的三角函数式,往往借助于因式分解.(4)化简结果的一般要求:①函数种类最少;②项数最少;③函数次数最低;④能求值的求出值;⑤尽量使分母不含三角函数;⑥尽量使分母不含根式.
2.
已知tan α=3,求下列各式的值:
题型三 已知α的正切值的求值问题
【例3】
点评 将所求三角函数式通过恒等变形,用已知三角函数表示出来,是一种整体思想,利用“1=sin2α+cos2α”将常数转化为三角函数,是一种重要的三角变换技巧,须切实领会和掌握,本例中,若由tan α=3分别求出sin α和cos α的值,则需讨论α是第一还是第三象限角,这无疑会增加计算量,走许多弯路.
已知tan α=2,求下列各式的值:
3.
已知sin α=m,|m|≤1,试用m表示cos α与tan α.
误区警示 因未按角α所在的象限分类讨论而出错
【示例】
纠错心得 当角α的某个三角函数的值含有字母,则应按字母的取值确定角α所在的象限,然后才好用这个字母表示角α的其它三角函数值.
根据同角三角函数的基本关系式,如果知道一个角的某一个三角函数值,可以求出这个角的其它两个三角函数值.在利用平方关系进行开方时,一定要注意判定角的范围,从而确定正确的符号.
课堂总结
1.
2.
