3.3.1 正弦函数、余弦函数的图象与性质(2)课件-湘教版必修2(19张PPT)
文档属性
| 名称 | 3.3.1 正弦函数、余弦函数的图象与性质(2)课件-湘教版必修2(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 688.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 21:00:45 | ||
图片预览






文档简介
3.3.1 正弦函数、余弦函数的图象与性质
知识回顾:
实数
角
任意实数x有唯一确定的sinx(或cosx)与之对应,
由此对应法则确定的函数y=sinx(或y=cosx)叫做正弦函数(或余弦函数),定义域是R.
正弦(或余弦)值
正弦函数,余弦函数的图象是怎样的呢?
抖动绳子、潮汐、舞动的彩带等都展现了波浪形的图形
这些图形和数学中正余弦函数图像非常相似!
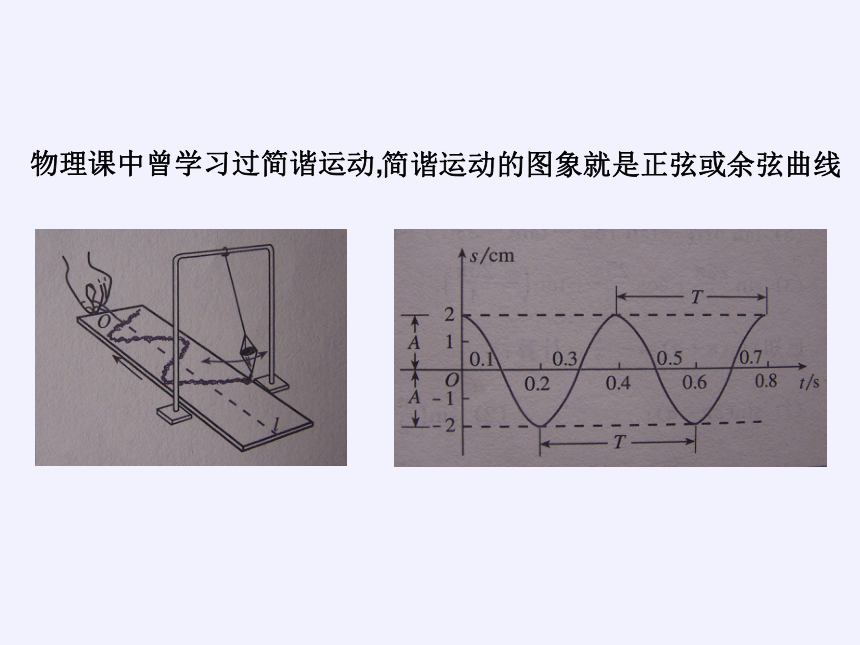
物理课中曾学习过简谐运动,
简谐运动的图象就是正弦或余弦曲线
0
1
1
M
P(x,y)
正弦线
MP=sin α;
余弦线
OM=cos α
2.函数值的正负跟正余弦线的方向有关,函数值的绝对值跟有向线段的长度相等
如何比较精确的作出正、余弦函数的图象呢?
1.三角函数线都是有向线段
在直角坐标系中如何作点 ?
C( , )
y=sinx x?[0,2?]
O1
O
y
x
-1
1
y=sinx x?R
终边相同角的三角函数值相等
即: sin(x+2k?)=sinx, k?Z
描图:用光滑曲线
将这些正弦线的终点连结起来
利用图象平移
A
B
借助上面作点C的方法,在直角坐标系中作出正弦函数
y=sinx x?[0,2?]
y=sinx x?R
正弦曲线
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y
x
o
1
-1
因为终边相同的角的三角函数值相同,所以y=sinx的图象在……,
…与y=sinx,x∈[0,2π]的图象相同
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦函数的图象
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=cosx=sin(x+ ), x?R
余弦曲线
正弦曲线
形状完全一样只是位置不同
由正弦函数图象得到余弦函数图象
思考 ?
在精确度要求不太高时,如何快速地作出正弦函数的图象呢?
在作出正弦函数的图象时,应抓住哪些
关键点?
正弦曲线
y
x
o
1
-1
(0,0)
( ,1)
( ? ,0)
( ,-1)
( 2? ,0)
五点画图法
五个关键点—
(0,0)
( ,1)
( ? ,0)
( ,1)
( 2? ,0)
(0,0)
( ,1)
( ? ,0)
( ,1)
( 2? ,0)
(0,0)
( ,1)
( ? ,0)
( ,1)
( 2? ,0)
(0,0)
( ,1)
( ? ,0)
( ,1)
( 2? ,0)
(0,0)
( ,1)
( ? ,0)
( ,-1)
( 2? ,0)
(0,0)
( ,1)
( ? ,0)
( ,-1)
( 2? ,0)
(0,0)
( ,1)
( ? ,0)
( ,-1)
( 2? ,0)
(0,0)
( ,1)
( ? ,0)
( ,-1)
( 2? ,0)
图象的最高点
与x轴的交点
图象的最低点
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦曲线
余弦曲线
(0,1)
( ,0)
( ? ,-1)
( ,0)
( 2? ,1)
图象的最高点
与x轴的交点
图象的最低点
五点作图法步骤:
(1)列表(列出关键五点)
(2)描点(描出五个关键点)
(3)连线(用光滑曲线顺次连五个点)
利用五点作图法画图
例: 画出函数y=1+sinx,x?[0, 2?]的简图:
x
sinx
1+sinx
0 ? 2 ?
0
1
0
-1
0
1 2 1 0 1
o
1
y
x
-1
2
步骤:
1.列表
2.描点
3.连线
y=sinx,x?[0, 2?]
y=1+sinx,x?[0, 2?]
练习: 画出函数y= - cosx,x?[0, 2?]的简图
x
cosx
- cosx
0 ? 2 ?
1
0
-1
0
1
-1 0 1 0 -1
y
x
o
1
-1
y= - cosx,x?[0, 2?]
y=cosx,x?[0, 2?]
变式训练
,
2、画出函数y=sin|x|,x∈R的图象
3、方程
的根的个数为( )
1、用五点法作函数 y=2sinx-1,x∈[0,2π]的简图
1. 正弦曲线、余弦曲线
几何法
五点法
2.注意与诱导公式、三角函数线等知识的联系
3.正、余弦函数的图象每相隔2π个单位重复出现,因此,只要记住它们在[0,2π]内的图象形态,就可以画出正弦曲线和余弦曲线.
4.作与正、余弦函数有关的题目时,函数图象是解题的基本要求,用“五点法”作图是常用的方法.
小结
作业:
必做题:画出下列函数的简图.
?⑴
? ⑵
选做题:用五点法画出函数
的图象.
在直角坐标系中如何作点 ?
P
M
C( , )
?
y
x
O
C( , )
谢 谢
知识回顾:
实数
角
任意实数x有唯一确定的sinx(或cosx)与之对应,
由此对应法则确定的函数y=sinx(或y=cosx)叫做正弦函数(或余弦函数),定义域是R.
正弦(或余弦)值
正弦函数,余弦函数的图象是怎样的呢?
抖动绳子、潮汐、舞动的彩带等都展现了波浪形的图形
这些图形和数学中正余弦函数图像非常相似!
物理课中曾学习过简谐运动,
简谐运动的图象就是正弦或余弦曲线
0
1
1
M
P(x,y)
正弦线
MP=sin α;
余弦线
OM=cos α
2.函数值的正负跟正余弦线的方向有关,函数值的绝对值跟有向线段的长度相等
如何比较精确的作出正、余弦函数的图象呢?
1.三角函数线都是有向线段
在直角坐标系中如何作点 ?
C( , )
y=sinx x?[0,2?]
O1
O
y
x
-1
1
y=sinx x?R
终边相同角的三角函数值相等
即: sin(x+2k?)=sinx, k?Z
描图:用光滑曲线
将这些正弦线的终点连结起来
利用图象平移
A
B
借助上面作点C的方法,在直角坐标系中作出正弦函数
y=sinx x?[0,2?]
y=sinx x?R
正弦曲线
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y
x
o
1
-1
因为终边相同的角的三角函数值相同,所以y=sinx的图象在……,
…与y=sinx,x∈[0,2π]的图象相同
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦函数的图象
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=cosx=sin(x+ ), x?R
余弦曲线
正弦曲线
形状完全一样只是位置不同
由正弦函数图象得到余弦函数图象
思考 ?
在精确度要求不太高时,如何快速地作出正弦函数的图象呢?
在作出正弦函数的图象时,应抓住哪些
关键点?
正弦曲线
y
x
o
1
-1
(0,0)
( ,1)
( ? ,0)
( ,-1)
( 2? ,0)
五点画图法
五个关键点—
(0,0)
( ,1)
( ? ,0)
( ,1)
( 2? ,0)
(0,0)
( ,1)
( ? ,0)
( ,1)
( 2? ,0)
(0,0)
( ,1)
( ? ,0)
( ,1)
( 2? ,0)
(0,0)
( ,1)
( ? ,0)
( ,1)
( 2? ,0)
(0,0)
( ,1)
( ? ,0)
( ,-1)
( 2? ,0)
(0,0)
( ,1)
( ? ,0)
( ,-1)
( 2? ,0)
(0,0)
( ,1)
( ? ,0)
( ,-1)
( 2? ,0)
(0,0)
( ,1)
( ? ,0)
( ,-1)
( 2? ,0)
图象的最高点
与x轴的交点
图象的最低点
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦曲线
余弦曲线
(0,1)
( ,0)
( ? ,-1)
( ,0)
( 2? ,1)
图象的最高点
与x轴的交点
图象的最低点
五点作图法步骤:
(1)列表(列出关键五点)
(2)描点(描出五个关键点)
(3)连线(用光滑曲线顺次连五个点)
利用五点作图法画图
例: 画出函数y=1+sinx,x?[0, 2?]的简图:
x
sinx
1+sinx
0 ? 2 ?
0
1
0
-1
0
1 2 1 0 1
o
1
y
x
-1
2
步骤:
1.列表
2.描点
3.连线
y=sinx,x?[0, 2?]
y=1+sinx,x?[0, 2?]
练习: 画出函数y= - cosx,x?[0, 2?]的简图
x
cosx
- cosx
0 ? 2 ?
1
0
-1
0
1
-1 0 1 0 -1
y
x
o
1
-1
y= - cosx,x?[0, 2?]
y=cosx,x?[0, 2?]
变式训练
,
2、画出函数y=sin|x|,x∈R的图象
3、方程
的根的个数为( )
1、用五点法作函数 y=2sinx-1,x∈[0,2π]的简图
1. 正弦曲线、余弦曲线
几何法
五点法
2.注意与诱导公式、三角函数线等知识的联系
3.正、余弦函数的图象每相隔2π个单位重复出现,因此,只要记住它们在[0,2π]内的图象形态,就可以画出正弦曲线和余弦曲线.
4.作与正、余弦函数有关的题目时,函数图象是解题的基本要求,用“五点法”作图是常用的方法.
小结
作业:
必做题:画出下列函数的简图.
?⑴
? ⑵
选做题:用五点法画出函数
的图象.
在直角坐标系中如何作点 ?
P
M
C( , )
?
y
x
O
C( , )
谢 谢
