3.3.1 正弦函数、余弦函数的图象与性质(3)课件-湘教版必修2(15张PPT)
文档属性
| 名称 | 3.3.1 正弦函数、余弦函数的图象与性质(3)课件-湘教版必修2(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 640.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览






文档简介
3.3.1 正弦函数、余弦函数的图象与性质
思考:下列图片中的现象有什么共同点?
每间隔相同的时间就会出现相同的现象称为周期现象.
我们学习的函数具有周期现象吗?如果有,我们就说它是周期函数,具有周期性。
今天我们就来研究正弦函数和余弦函数的周期性。
思考?
知识回顾.
正弦函数、余弦函数的图象
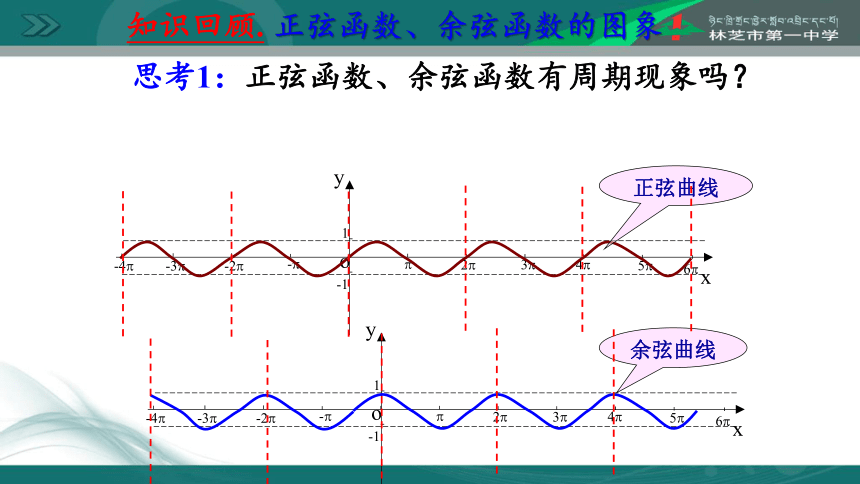
思考1:正弦函数、余弦函数有周期现象吗?
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦曲线
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
正弦曲线
一、周期函数
一般地,对于函数f(x),如果存在一个非零的常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数,
最小正周期
对于一个周期函数f(x),如果在它所有的周期中存在一个最小的正数,那么这个最小的正数就叫做f(x)的最小正周期。
非零常数T叫做这个函数的周期。
1﹑sinx,cosx 的周期是2π ﹑4π ﹑6π ﹑
-2π﹑-4π﹑-6π……2kπ.
2﹑如果T是函数f (x) 的周期,那么……,-4T、-2T、2T ﹑ 3T ,……,kT也是函数f(x)的周期.
思考:一个周期函数的周期有多少个?
正弦函数和余弦函数的周期都是 2kπ,最小正周期都是2π
说明:我们现在谈到三角函数周期时,如果不加特别说明,一般都是指的最小正周期。
概念强化
1.f(x+T)=f(x)对每一个x都成立时候,才可以说T是f(x)的周期。
2.只有个别的x满足f(x+T)=f(x)时,不能判断T是否是f(x)的周期。
判断正误
提示:只需判断对每一个x,是否都有f(x+T)=f(x)成立。
×
√
例1 求下列函数的周期:
周期函数的周期性在图像上能直观体现出来,如果能画出它们的图像,就可直观的看出周期。
看1
看2
看3
函数
w值
周期T
w T
y=3cosx
y=sin2x
1
2
×
小组合作,寻找规律
结论:
例1:求下列函数的周期
课堂练习:
最小正周期是:
一般地,函数 及 (其中 为常数,且 )的周期是
归纳总结
解析:
B
1.周期函数、最小正周期的定义;
课堂小结:
和
型函数的周期的求法。
最小正周期:
作业:
求下列函数的周期
(3)y=|sinx|
谢 谢
思考:下列图片中的现象有什么共同点?
每间隔相同的时间就会出现相同的现象称为周期现象.
我们学习的函数具有周期现象吗?如果有,我们就说它是周期函数,具有周期性。
今天我们就来研究正弦函数和余弦函数的周期性。
思考?
知识回顾.
正弦函数、余弦函数的图象
思考1:正弦函数、余弦函数有周期现象吗?
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦曲线
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
正弦曲线
一、周期函数
一般地,对于函数f(x),如果存在一个非零的常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数,
最小正周期
对于一个周期函数f(x),如果在它所有的周期中存在一个最小的正数,那么这个最小的正数就叫做f(x)的最小正周期。
非零常数T叫做这个函数的周期。
1﹑sinx,cosx 的周期是2π ﹑4π ﹑6π ﹑
-2π﹑-4π﹑-6π……2kπ.
2﹑如果T是函数f (x) 的周期,那么……,-4T、-2T、2T ﹑ 3T ,……,kT也是函数f(x)的周期.
思考:一个周期函数的周期有多少个?
正弦函数和余弦函数的周期都是 2kπ,最小正周期都是2π
说明:我们现在谈到三角函数周期时,如果不加特别说明,一般都是指的最小正周期。
概念强化
1.f(x+T)=f(x)对每一个x都成立时候,才可以说T是f(x)的周期。
2.只有个别的x满足f(x+T)=f(x)时,不能判断T是否是f(x)的周期。
判断正误
提示:只需判断对每一个x,是否都有f(x+T)=f(x)成立。
×
√
例1 求下列函数的周期:
周期函数的周期性在图像上能直观体现出来,如果能画出它们的图像,就可直观的看出周期。
看1
看2
看3
函数
w值
周期T
w T
y=3cosx
y=sin2x
1
2
×
小组合作,寻找规律
结论:
例1:求下列函数的周期
课堂练习:
最小正周期是:
一般地,函数 及 (其中 为常数,且 )的周期是
归纳总结
解析:
B
1.周期函数、最小正周期的定义;
课堂小结:
和
型函数的周期的求法。
最小正周期:
作业:
求下列函数的周期
(3)y=|sinx|
谢 谢
