3.3.1正弦函数、余弦函数的图象与性质_课件1-湘教版必修2(23张PPT)
文档属性
| 名称 | 3.3.1正弦函数、余弦函数的图象与性质_课件1-湘教版必修2(23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览








文档简介
1.会用正弦线画正弦曲线,会利用平移作余弦函数的图象.
2.会用“五点法”画正弦曲线、余弦曲线的简图.
正弦函数、余弦函数的图象与性质
正弦函数图象的画法
(1)几何法—借助三角函数线;
(2)描点法—五点法.
函数y=sin x,x∈[0,2π]的图象上起关键作用的点有以下五个:
自学导引
1.
余弦函数图象的画法
(1)依据诱导公式cos x=sin ,要得到y=cos x的图象,只须把y=sin x的图象向__平移 个单位长度即可.
(2)用“五点法”画出余弦函数y=cos x在[0,2π]上的图象时所取的五个关键点分别为:
2.
左
函数y=sin x+2|sin x|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,求k的取值范围.
自主探究
在同一坐标系里作出函数y=sin x+2|sin x|,x∈[0,2π]的图象与直线y=k.
由图可知,当函数y=sin x+2|sin x|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点时,k的取值范围是
1<k<3.
正弦曲线上最高点的纵坐标是 ( ).
预习测评
1.
答案 D
y=1+sin x,x∈[0,2π)的图象与直线y= 有______个交点 ( ).
A.1 B.2 C.3 D.0
答案 B
在[0,2π]上,f(x)=cos x的零点有________个 ( ).
A.0 B.1 C.2 D.3
答案 C
2.
3.
在“五点法”中对于正弦曲线,最低点的横坐标与最高点的横坐标的差等于 ( ).
4.
答案 B
正弦曲线的几何作法
利用单位圆中的正弦线,可以作出正弦函数y=sin x在[0,2π]上的图象,具体分为如下五个步骤:
(1)作直角坐标系,并在直角坐标系中y轴左侧画单位圆.
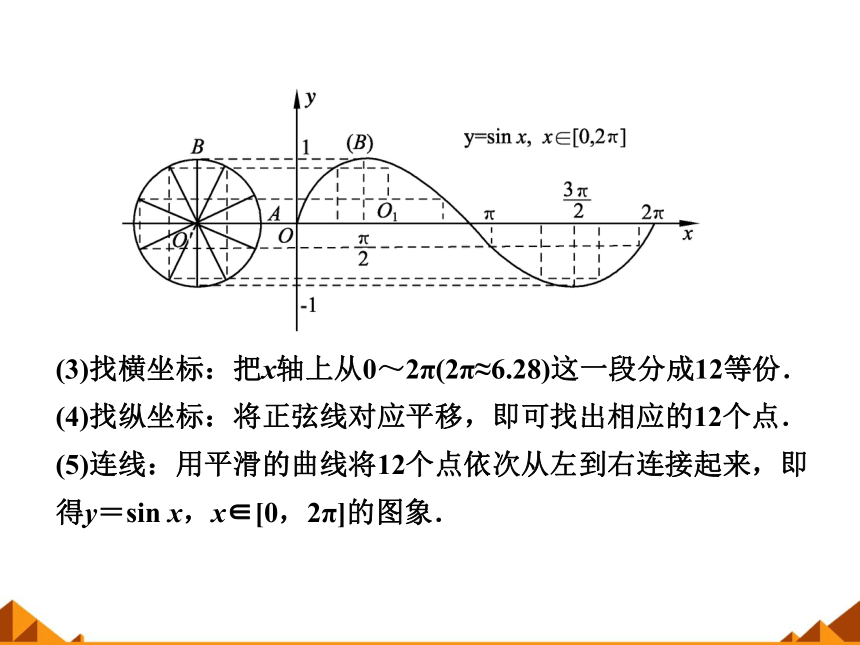
(2)把单位圆分成12等份(等份越多,画出的图象越精确)如图.过单位圆上的各分点作x轴的垂线,可以得到对应于0, …,2π等角的正弦线.
名师点睛
1.
(3)找横坐标:把x轴上从0~2π(2π≈6.28)这一段分成12等份.
(4)找纵坐标:将正弦线对应平移,即可找出相应的12个点.
(5)连线:用平滑的曲线将12个点依次从左到右连接起来,即得y=sin x,x∈[0,2π]的图象.
我们通过图象的平移作正弦函数y=sin x,x∈R的图象.因为终边相同的角的三角函数值相等,所以函数y=sin x,x∈[2kπ,2(k+1)π],k∈Z且k≠0的图象与函数y=sin x,x∈[0,2π]的图象的形状完全一样,只是位置不同,于是我们只要将函数y=sin x,x∈[0,2π]的图象向左、右平移(每次平移2π个单位长度),就可以得到正弦函数y=sin x,x∈R的图象,正弦函数y=sin x,x∈R的图象叫做正弦曲线.
下图是正弦曲线y=sin x,(x∈R)的图象:
“五点法”
在精确度要求不太高的情况下,可用五点法作出y=sin x的图象,x∈[0,2π]的图象上有五点起决定作用,它们是(0,0)、 (2π,0).描出这五
2.
点后,其图象的形状基本上就确定了.
因此,在精确度要求不太高时,我们常常先描出这五个点,然后用平滑的曲线将它们连接起来,就得到在相应区间内正弦函数的简图,这种方法叫做“五点法”.
作出下列函数的简图.
(1)y=1-sin x,x∈[0,2π];
(2)y=-1-cos x,x∈[0,2π].
解 (1)利用“五点法”作图
列表:
?
题型一 “五点法”作图
【例1】
典例剖析
描点作图,如图所示:
(2)列表:
描点作图,如图所示.
点评 作正弦、余弦曲线要理解几何法作图,掌握五点法作图.“五点”即y=sin x或y=cos x的图象在一个最小正周期内的最高点、最低点和与x轴的交点.“五点法”是作简图的常用方法.
作出函数y= 的图象.
解 原函数可化为y=|sin x|,
作出函数y=sin x的图象,再将x轴下方的图象翻折到x轴上方,其图象如图:
1.
求函数y=lg sin x+ 的定义域.
题型二 利用图象求定义域
【例2】
点评 求有关正弦函数、余弦函数的定义域问题,就是先列出使函数解析式有意义的关于sin x和cos x的不等式或不等式组,再借助正弦曲线、余弦曲线找出使不等式成立的x的取值范围.此类问题也可借助单位圆中的正弦线、余弦线求解.
函数y= 的定义域是______________.
2.
在同一坐标系中,作函数y=sin x和y=lg x的图象,根据图象判断出方程sin x=lg x的解的个数.
解 建立坐标系xOy,先用五点法画出函数y=sin x,x∈[0,2π)的图象,再依次向左、右连续平移2π个单位,得到y=sin x的图象.
题型三 利用三角函数的图象判断方程解的个数
【例3】
由图象可知方程sin x=lg x的解有3个.
点评 三角函数的图象是研究函数的重要工具,通过图象可较简便的解决问题,这正是数形结合思想方法的应用.
方程sin x=x的实数解的个数为 ( ).
A.1 B.2 C.3 D.5
解析 在同一平面直角坐标系中,作出直线y=x和正弦曲线y=sin x,观察图象可知,x=0是方程的一个实数解.而在(0,+∞)上总有sin x答案 A
3.
当x∈[ ,π]时,sin x=2m-1,求实数m的取值范围.
错解 因为-1≤sin x≤1,所以-1≤2m-1≤1,解得m的取值范围0≤m≤1.
误区警示 不注意三角函数的取值范围而出错
【示例】
纠错心得 三角函数的取值范围与定义域有关,因此,在求解有关范围问题时,一定要先看清定义域,再由定义域推得三角函数的取值范围,最后求出正确答案.
正弦曲线和余弦曲线的形状完全相同,只是在同一直角坐标系下的位置不同.
三角函数图象直观地反映了三角函数的性质,所以画好三角函数的图象是研究三角函数性质的关键,因此一定要掌握正弦、余弦函数的图象特征,特别是会灵活运用五点作图法准确作出函数图象.
关键点指的是图象的最高点、最低点及与x轴的交点.
利用正弦曲线、余弦曲线,可以根据三角函数值的范围判断角的范围,也可以判断某些超越方程实数解的个数.要求准确作图,数形结合,综合分析.
课堂总结
1.
2.
3.
4.
2.会用“五点法”画正弦曲线、余弦曲线的简图.
正弦函数、余弦函数的图象与性质
正弦函数图象的画法
(1)几何法—借助三角函数线;
(2)描点法—五点法.
函数y=sin x,x∈[0,2π]的图象上起关键作用的点有以下五个:
自学导引
1.
余弦函数图象的画法
(1)依据诱导公式cos x=sin ,要得到y=cos x的图象,只须把y=sin x的图象向__平移 个单位长度即可.
(2)用“五点法”画出余弦函数y=cos x在[0,2π]上的图象时所取的五个关键点分别为:
2.
左
函数y=sin x+2|sin x|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,求k的取值范围.
自主探究
在同一坐标系里作出函数y=sin x+2|sin x|,x∈[0,2π]的图象与直线y=k.
由图可知,当函数y=sin x+2|sin x|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点时,k的取值范围是
1<k<3.
正弦曲线上最高点的纵坐标是 ( ).
预习测评
1.
答案 D
y=1+sin x,x∈[0,2π)的图象与直线y= 有______个交点 ( ).
A.1 B.2 C.3 D.0
答案 B
在[0,2π]上,f(x)=cos x的零点有________个 ( ).
A.0 B.1 C.2 D.3
答案 C
2.
3.
在“五点法”中对于正弦曲线,最低点的横坐标与最高点的横坐标的差等于 ( ).
4.
答案 B
正弦曲线的几何作法
利用单位圆中的正弦线,可以作出正弦函数y=sin x在[0,2π]上的图象,具体分为如下五个步骤:
(1)作直角坐标系,并在直角坐标系中y轴左侧画单位圆.
(2)把单位圆分成12等份(等份越多,画出的图象越精确)如图.过单位圆上的各分点作x轴的垂线,可以得到对应于0, …,2π等角的正弦线.
名师点睛
1.
(3)找横坐标:把x轴上从0~2π(2π≈6.28)这一段分成12等份.
(4)找纵坐标:将正弦线对应平移,即可找出相应的12个点.
(5)连线:用平滑的曲线将12个点依次从左到右连接起来,即得y=sin x,x∈[0,2π]的图象.
我们通过图象的平移作正弦函数y=sin x,x∈R的图象.因为终边相同的角的三角函数值相等,所以函数y=sin x,x∈[2kπ,2(k+1)π],k∈Z且k≠0的图象与函数y=sin x,x∈[0,2π]的图象的形状完全一样,只是位置不同,于是我们只要将函数y=sin x,x∈[0,2π]的图象向左、右平移(每次平移2π个单位长度),就可以得到正弦函数y=sin x,x∈R的图象,正弦函数y=sin x,x∈R的图象叫做正弦曲线.
下图是正弦曲线y=sin x,(x∈R)的图象:
“五点法”
在精确度要求不太高的情况下,可用五点法作出y=sin x的图象,x∈[0,2π]的图象上有五点起决定作用,它们是(0,0)、 (2π,0).描出这五
2.
点后,其图象的形状基本上就确定了.
因此,在精确度要求不太高时,我们常常先描出这五个点,然后用平滑的曲线将它们连接起来,就得到在相应区间内正弦函数的简图,这种方法叫做“五点法”.
作出下列函数的简图.
(1)y=1-sin x,x∈[0,2π];
(2)y=-1-cos x,x∈[0,2π].
解 (1)利用“五点法”作图
列表:
?
题型一 “五点法”作图
【例1】
典例剖析
描点作图,如图所示:
(2)列表:
描点作图,如图所示.
点评 作正弦、余弦曲线要理解几何法作图,掌握五点法作图.“五点”即y=sin x或y=cos x的图象在一个最小正周期内的最高点、最低点和与x轴的交点.“五点法”是作简图的常用方法.
作出函数y= 的图象.
解 原函数可化为y=|sin x|,
作出函数y=sin x的图象,再将x轴下方的图象翻折到x轴上方,其图象如图:
1.
求函数y=lg sin x+ 的定义域.
题型二 利用图象求定义域
【例2】
点评 求有关正弦函数、余弦函数的定义域问题,就是先列出使函数解析式有意义的关于sin x和cos x的不等式或不等式组,再借助正弦曲线、余弦曲线找出使不等式成立的x的取值范围.此类问题也可借助单位圆中的正弦线、余弦线求解.
函数y= 的定义域是______________.
2.
在同一坐标系中,作函数y=sin x和y=lg x的图象,根据图象判断出方程sin x=lg x的解的个数.
解 建立坐标系xOy,先用五点法画出函数y=sin x,x∈[0,2π)的图象,再依次向左、右连续平移2π个单位,得到y=sin x的图象.
题型三 利用三角函数的图象判断方程解的个数
【例3】
由图象可知方程sin x=lg x的解有3个.
点评 三角函数的图象是研究函数的重要工具,通过图象可较简便的解决问题,这正是数形结合思想方法的应用.
方程sin x=x的实数解的个数为 ( ).
A.1 B.2 C.3 D.5
解析 在同一平面直角坐标系中,作出直线y=x和正弦曲线y=sin x,观察图象可知,x=0是方程的一个实数解.而在(0,+∞)上总有sin x
3.
当x∈[ ,π]时,sin x=2m-1,求实数m的取值范围.
错解 因为-1≤sin x≤1,所以-1≤2m-1≤1,解得m的取值范围0≤m≤1.
误区警示 不注意三角函数的取值范围而出错
【示例】
纠错心得 三角函数的取值范围与定义域有关,因此,在求解有关范围问题时,一定要先看清定义域,再由定义域推得三角函数的取值范围,最后求出正确答案.
正弦曲线和余弦曲线的形状完全相同,只是在同一直角坐标系下的位置不同.
三角函数图象直观地反映了三角函数的性质,所以画好三角函数的图象是研究三角函数性质的关键,因此一定要掌握正弦、余弦函数的图象特征,特别是会灵活运用五点作图法准确作出函数图象.
关键点指的是图象的最高点、最低点及与x轴的交点.
利用正弦曲线、余弦曲线,可以根据三角函数值的范围判断角的范围,也可以判断某些超越方程实数解的个数.要求准确作图,数形结合,综合分析.
课堂总结
1.
2.
3.
4.
