3.4.1三角函数的周期性课件-湘教版必修2(30张PPT)
文档属性
| 名称 | 3.4.1三角函数的周期性课件-湘教版必修2(30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览










文档简介
三角函数的周期性
世界上有许多事物都呈现“周而复始”的变化规律,如年有四季更替,月有阴晴圆缺.这种现象在数学上称为周期性,在函数领域里,周期性是函数的一个重要性质.
若记f(x)=sinx,则对于任意实数x,都有f(x+2∏)=f(x)
思考:如何用数学语言刻画函数的周期性?
定义:对于函数f(x),如果存在一个——————,使得当x取定义域内的 ————值时,都有f(x)=f(x+T),那么函数 f(x)就叫做周期函数,—————叫做这个函数的周期。
一、周期函数的定义
注意:
1.T必须是常数,且不为零
2.对周期函数来说f(x+T)=f(x)必须对定义域内的任意x都成立
非零常数T
每一个
非零常数T
?判断下列说法是否正确
(1) 时, ,则 一定不是 的周期
( )
√
( )
(2) 时, ,则
一定是 的周期
×
注意:在周期函数和周期定义中,要特别注意“每一个x的值”.
问题1: 2π是不是正弦函数和余弦函数的周期?
2π是正弦函数和余弦函数的周期.
问题2: 2kπ(k≠0且k∈Z) 是不是正弦函数和余弦函数的周期?
2kπ(k≠0且k∈Z) 都是正弦函数和余弦函数的周期.
若T为函数f(x)的周期,则kT(k≠0且k∈Z) 都是函数f(x)的周期.
问题3: 一个周期函数的周期有多少个?
有无数个
对于一个周期函数f(x),如果在它所有的周期中存在一个最小的正数,那么这个最小的正数就叫做f(x)的最小正周期。
最小正周期
结论: 2π是正弦、余弦函数的最小正周期.
说明:今后所说周期,如不作特殊说明,均指最小正周期.
问题4: 是否每一个周期函数都有最小正周期?
下面函数是周期函数吗?如果是周期函数,你能找出最小正周期吗?
否
常数函数没有最小正周期
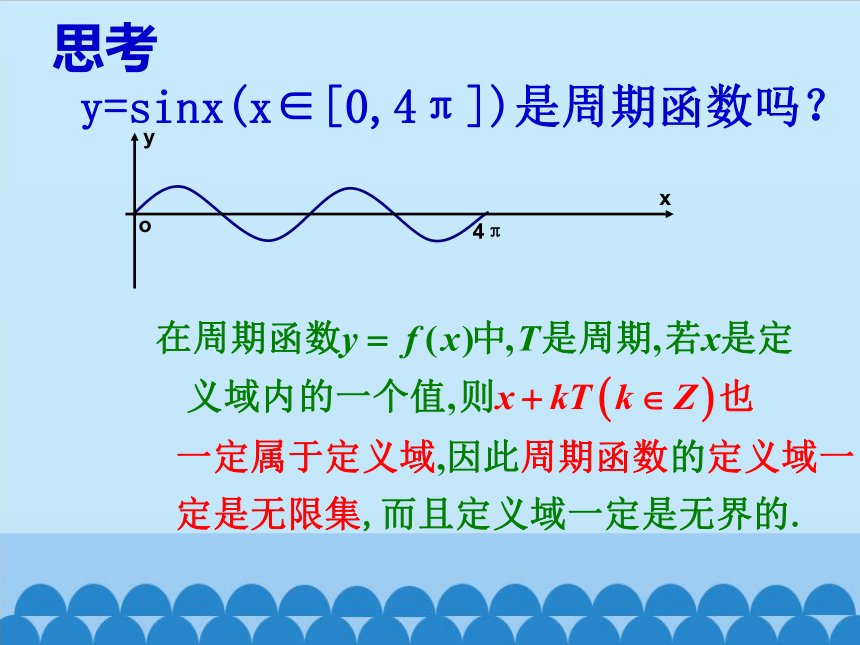
思考
y=sinx(x∈[0,4π])是周期函数吗?
o
y
x
4π
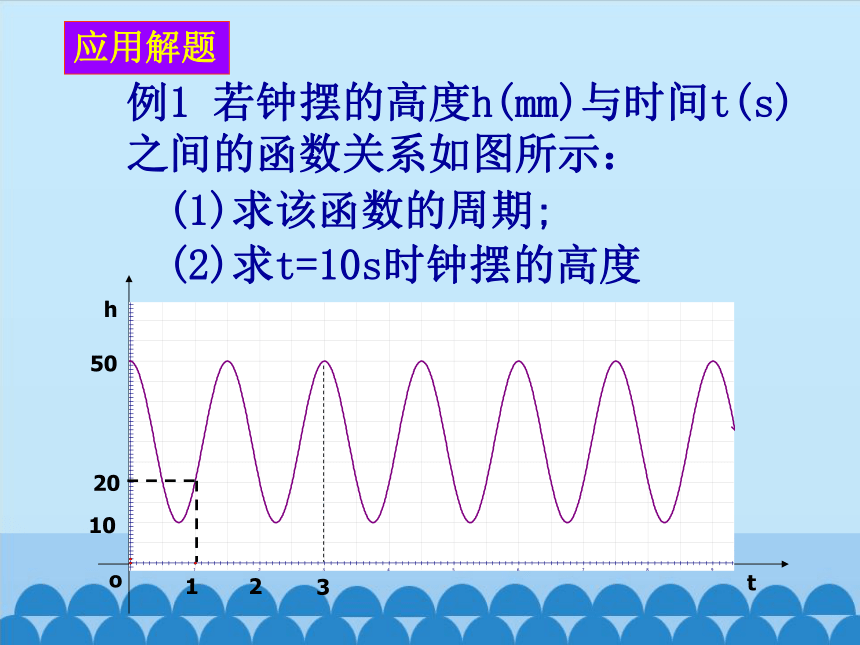
例1 若钟摆的高度h(mm)与时间t(s)之间的函数关系如图所示:
(1)求该函数的周期;
(2)求t=10s时钟摆的高度
1
2
3
t
h
o
10
50
20
应用解题
解:(1)由图象可知,该函数的周期为1.5s.
(2)设h=f(t), 由函数的周期为1.5s,可知f(10)=f(1+6×1.5)=f(1)=20,
故t=10s时钟摆的高度为20mm.
应用
你能从上面的解答过程中归纳一下这些函数的周期与解析式中的哪些量有关系吗?
二、函数周期性的概念的推广
y=4cosx
y=sin4x
函数
周期
2 π
π /2
6π
结论:
函数y=Asin(ωx+φ),x∈R及函数y=Acos(ωx+φ),x∈R(其中A,ω, φ为常数,且A≠0,ω ≠ 0)的周期为
当ω<0周期为
结论:
函数y=Atan(ωx+φ),x∈R(其中A,ω, φ为常数,且A≠0,ω ≠ 0)的周期为T=π/|ω|
一般地,函数 y=Asin(ωx+φ) 及y=Acos(ωx+φ) (其中A ,ω,φ为常数,且 A≠0, ω≠0 )的周期是:
周期求法:
1.定义法:
2.公式法:
函数y=Atan(ωx+φ) (A≠0, ω≠0)周期为
2. 若函数 的最小正
周期为 ,求正数 的值。
1.求下列函数的最小正周期
练习
三、函数周期性(抽象函数)
1、 一般地,对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x)=f(x+T),那么函数f(x)就叫做周期函数.非零常数T叫做这个函数的周期.
2、周期函数的周期与函数的定义域有关,周期函数不一定存在最小正周期.
3、函数y=Asin(ωx+Ψ),x∈R及函数y=Acos(ωx+Ψ),x∈R(其中A,ω,Ψ为常数,且A≠0,ω>0)的周期T=2π/ω.
回顾小结
谢谢
世界上有许多事物都呈现“周而复始”的变化规律,如年有四季更替,月有阴晴圆缺.这种现象在数学上称为周期性,在函数领域里,周期性是函数的一个重要性质.
若记f(x)=sinx,则对于任意实数x,都有f(x+2∏)=f(x)
思考:如何用数学语言刻画函数的周期性?
定义:对于函数f(x),如果存在一个——————,使得当x取定义域内的 ————值时,都有f(x)=f(x+T),那么函数 f(x)就叫做周期函数,—————叫做这个函数的周期。
一、周期函数的定义
注意:
1.T必须是常数,且不为零
2.对周期函数来说f(x+T)=f(x)必须对定义域内的任意x都成立
非零常数T
每一个
非零常数T
?判断下列说法是否正确
(1) 时, ,则 一定不是 的周期
( )
√
( )
(2) 时, ,则
一定是 的周期
×
注意:在周期函数和周期定义中,要特别注意“每一个x的值”.
问题1: 2π是不是正弦函数和余弦函数的周期?
2π是正弦函数和余弦函数的周期.
问题2: 2kπ(k≠0且k∈Z) 是不是正弦函数和余弦函数的周期?
2kπ(k≠0且k∈Z) 都是正弦函数和余弦函数的周期.
若T为函数f(x)的周期,则kT(k≠0且k∈Z) 都是函数f(x)的周期.
问题3: 一个周期函数的周期有多少个?
有无数个
对于一个周期函数f(x),如果在它所有的周期中存在一个最小的正数,那么这个最小的正数就叫做f(x)的最小正周期。
最小正周期
结论: 2π是正弦、余弦函数的最小正周期.
说明:今后所说周期,如不作特殊说明,均指最小正周期.
问题4: 是否每一个周期函数都有最小正周期?
下面函数是周期函数吗?如果是周期函数,你能找出最小正周期吗?
否
常数函数没有最小正周期
思考
y=sinx(x∈[0,4π])是周期函数吗?
o
y
x
4π
例1 若钟摆的高度h(mm)与时间t(s)之间的函数关系如图所示:
(1)求该函数的周期;
(2)求t=10s时钟摆的高度
1
2
3
t
h
o
10
50
20
应用解题
解:(1)由图象可知,该函数的周期为1.5s.
(2)设h=f(t), 由函数的周期为1.5s,可知f(10)=f(1+6×1.5)=f(1)=20,
故t=10s时钟摆的高度为20mm.
应用
你能从上面的解答过程中归纳一下这些函数的周期与解析式中的哪些量有关系吗?
二、函数周期性的概念的推广
y=4cosx
y=sin4x
函数
周期
2 π
π /2
6π
结论:
函数y=Asin(ωx+φ),x∈R及函数y=Acos(ωx+φ),x∈R(其中A,ω, φ为常数,且A≠0,ω ≠ 0)的周期为
当ω<0周期为
结论:
函数y=Atan(ωx+φ),x∈R(其中A,ω, φ为常数,且A≠0,ω ≠ 0)的周期为T=π/|ω|
一般地,函数 y=Asin(ωx+φ) 及y=Acos(ωx+φ) (其中A ,ω,φ为常数,且 A≠0, ω≠0 )的周期是:
周期求法:
1.定义法:
2.公式法:
函数y=Atan(ωx+φ) (A≠0, ω≠0)周期为
2. 若函数 的最小正
周期为 ,求正数 的值。
1.求下列函数的最小正周期
练习
三、函数周期性(抽象函数)
1、 一般地,对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x)=f(x+T),那么函数f(x)就叫做周期函数.非零常数T叫做这个函数的周期.
2、周期函数的周期与函数的定义域有关,周期函数不一定存在最小正周期.
3、函数y=Asin(ωx+Ψ),x∈R及函数y=Acos(ωx+Ψ),x∈R(其中A,ω,Ψ为常数,且A≠0,ω>0)的周期T=2π/ω.
回顾小结
谢谢
