4.3向量与实数相乘_课件1(1)-湘教版必修2(30张PPT)
文档属性
| 名称 | 4.3向量与实数相乘_课件1(1)-湘教版必修2(30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 670.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览










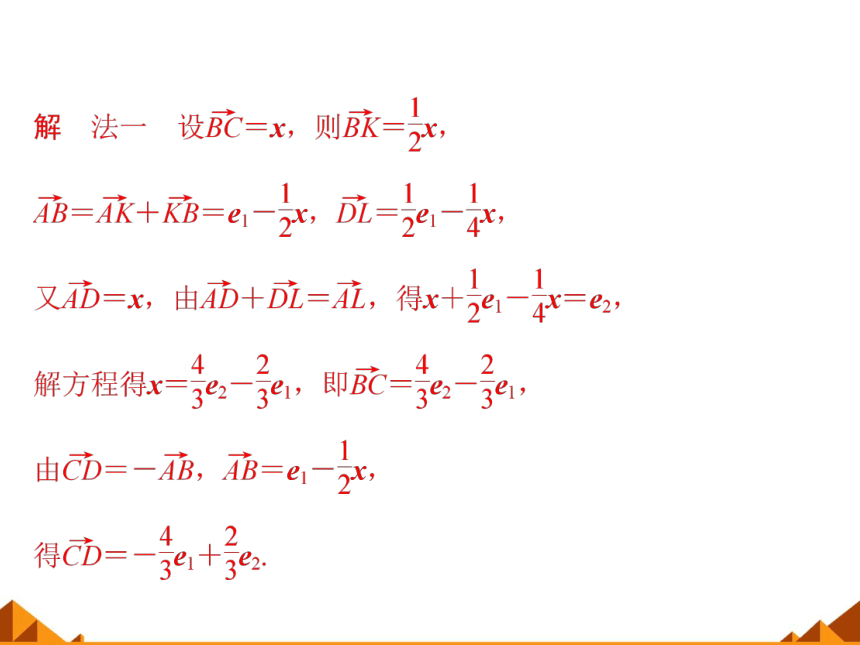
文档简介
向量与实数相乘
[学习目标]
1.掌握向量与实数相乘运算及其几何意义,掌握向量与实数相乘运算的运算律,能熟练地进行向量与实数相乘运算.
2.掌握平行向量的条件,会根据平行向量的条件判断两个向量是否平行或点共线.
3.理解单位向量的概念及意义.
[知识链接]
1.已知非零向量a,作出a+a+a和(-a)+(-a)+(-a),你能说明它们与向量a之间的关系吗?
2.已知非零向量a,你能说明实数λ与向量a的乘积λa的几何意义吗?
答 λa仍然是一个向量.
当λ>0时,λa与a的方向相同;
当λ<0时,λa与a的方向相反;
当λ=0时,λa=0,方向任意.
|λa|=|λ|·|a|.
[预习导引]
1.向量与实数相乘运算
(1)将向量v乘以一个正数λ,得到一个向量λv,它的方向与 v ,长度|λv|是|v|的 倍.
(2)将向量v乘以一个负数λ,得到一个向量λv,它的方向与v ,长度|λv|是|v|的 倍.
(3)向量v乘以0得到的0v是 .
相同
λ
相反
|λ|
零向量
规律方法 向量的初等运算类似于实数的运算,其化简的方法与代数式的化简类似,可以进行加、减、数乘等运算,也满足运算律,可以进行去括号、移项、合并同类项等变形手段.
规律方法
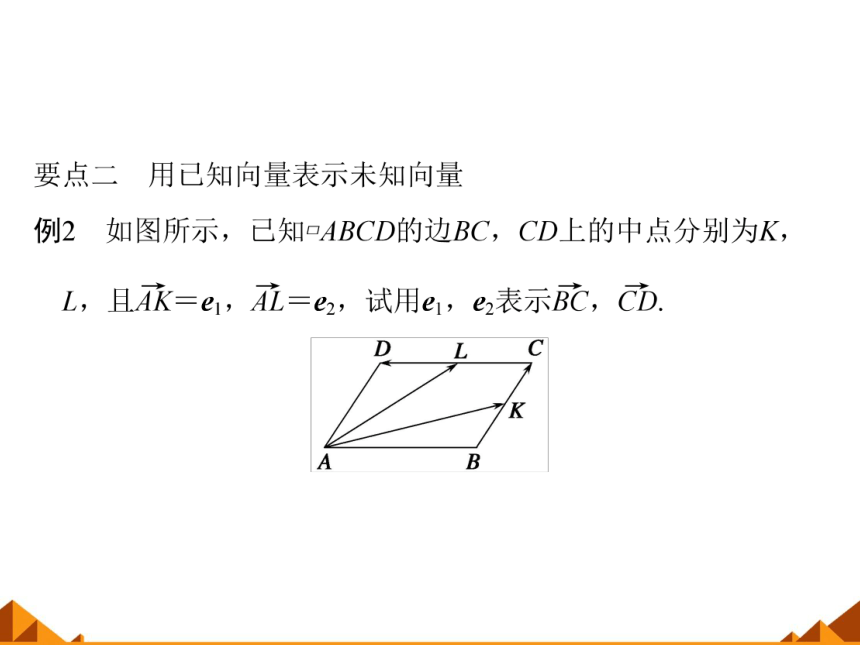
(1)由已知量表示未知量时,要善于利用三角形法则、平行四边形法则,以及向量线性运算的运算律,还应重视平面几何知识的应用,如法三.
(2)当直接表示较困难时,应考虑利用方程(组)求解,如本题法一、法二.
规律方法
(1)本题充分利用了平行向量的条件,因此用它既可以证明点共线或线共线问题,也可以根据共线求参数的值.
(2)向量共线的判断(证明)是把两向量用共同的已知向量来表示,进而互相表示,从而判断共线.
4.已知向量a,b不共线,且c=λa+b,d=a+(2λ-1)b,若c与d同向,求实数λ的值.
再见
[学习目标]
1.掌握向量与实数相乘运算及其几何意义,掌握向量与实数相乘运算的运算律,能熟练地进行向量与实数相乘运算.
2.掌握平行向量的条件,会根据平行向量的条件判断两个向量是否平行或点共线.
3.理解单位向量的概念及意义.
[知识链接]
1.已知非零向量a,作出a+a+a和(-a)+(-a)+(-a),你能说明它们与向量a之间的关系吗?
2.已知非零向量a,你能说明实数λ与向量a的乘积λa的几何意义吗?
答 λa仍然是一个向量.
当λ>0时,λa与a的方向相同;
当λ<0时,λa与a的方向相反;
当λ=0时,λa=0,方向任意.
|λa|=|λ|·|a|.
[预习导引]
1.向量与实数相乘运算
(1)将向量v乘以一个正数λ,得到一个向量λv,它的方向与 v ,长度|λv|是|v|的 倍.
(2)将向量v乘以一个负数λ,得到一个向量λv,它的方向与v ,长度|λv|是|v|的 倍.
(3)向量v乘以0得到的0v是 .
相同
λ
相反
|λ|
零向量
规律方法 向量的初等运算类似于实数的运算,其化简的方法与代数式的化简类似,可以进行加、减、数乘等运算,也满足运算律,可以进行去括号、移项、合并同类项等变形手段.
规律方法
(1)由已知量表示未知量时,要善于利用三角形法则、平行四边形法则,以及向量线性运算的运算律,还应重视平面几何知识的应用,如法三.
(2)当直接表示较困难时,应考虑利用方程(组)求解,如本题法一、法二.
规律方法
(1)本题充分利用了平行向量的条件,因此用它既可以证明点共线或线共线问题,也可以根据共线求参数的值.
(2)向量共线的判断(证明)是把两向量用共同的已知向量来表示,进而互相表示,从而判断共线.
4.已知向量a,b不共线,且c=λa+b,d=a+(2λ-1)b,若c与d同向,求实数λ的值.
再见
