4.2向量的加法_课件1-湘教版必修2(25张PPT)
文档属性
| 名称 | 4.2向量的加法_课件1-湘教版必修2(25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览






文档简介
1.掌握向量的加法运算,能够运用三角形法则和平行四
边形法则作向量的和向量.
2.掌握向量加法的运算律,能熟练地运用它们进行向量
运算.
向量的加法
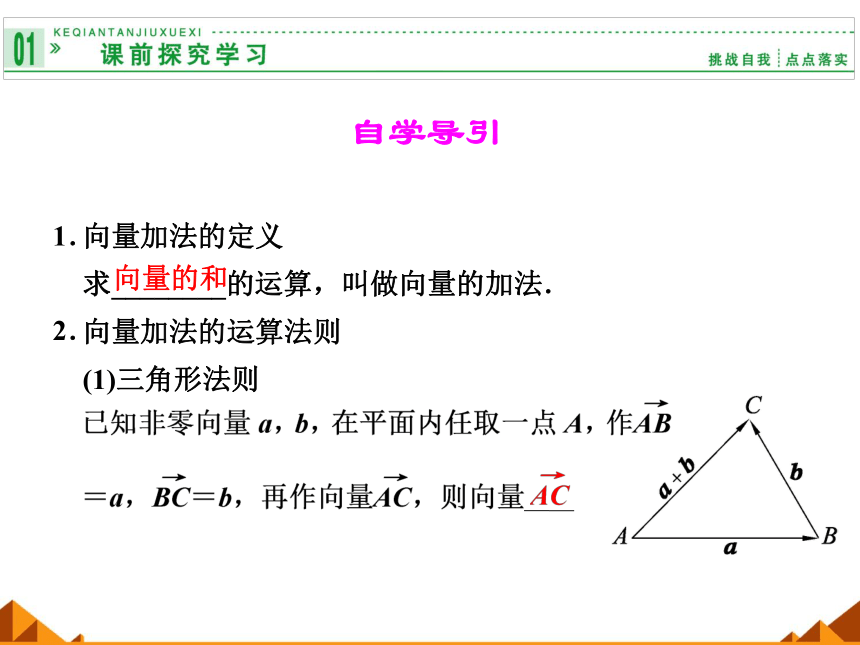
向量加法的定义
求________的运算,叫做向量的加法.
向量加法的运算法则
(1)三角形法则
自学导引
1.
2.
向量的和
叫做a与b的和(或和向量),记作_____,即a+b=
.上述求两个向量和的作图法则,叫做向量求和的三角形法则.对于零向量与任一向量a的和有a +0 =__ +_=_.
(2)平行四边形法则
a+b
0
a
a
以___,___为邻边作__________,则对角线上的向量
AB
AD
平行四边形
=a+b,如图所示.这个法则叫做两个向量求和的平行四边形法则.
向量加法的运算律
(1)交换律:a+b=____.
(2)结合律:(____)+c=a+(____).
(3)当a与b反向时,若|a|≥|b|,则a+b与a的方向____,且
|a+b|=______.
若|a|<|b|,则a+b与_的方向相同,且|a+b|=______.
3.
b+a
a+b
b+c
相同
|a|-|b|
b
|b|-|a|
用向量加法的三角形法则和平行四边形法则求a+b,所得的结果一样吗?为什么?
提示 所得结果完全一样.
理由是,在如图的三角形法则中所得的三角形ABC与四边形法则所得的平行四边形ABCD中的三角形ABC是全等的.
自主探究
在△ABC中,下列运算正确的是 ( ).
预习测评
1.
答案 D
已知向量a表示“向东航行1 km”,向量b表示“向南航行1 km”,则a+b表示 ( ).
2.
答案 A
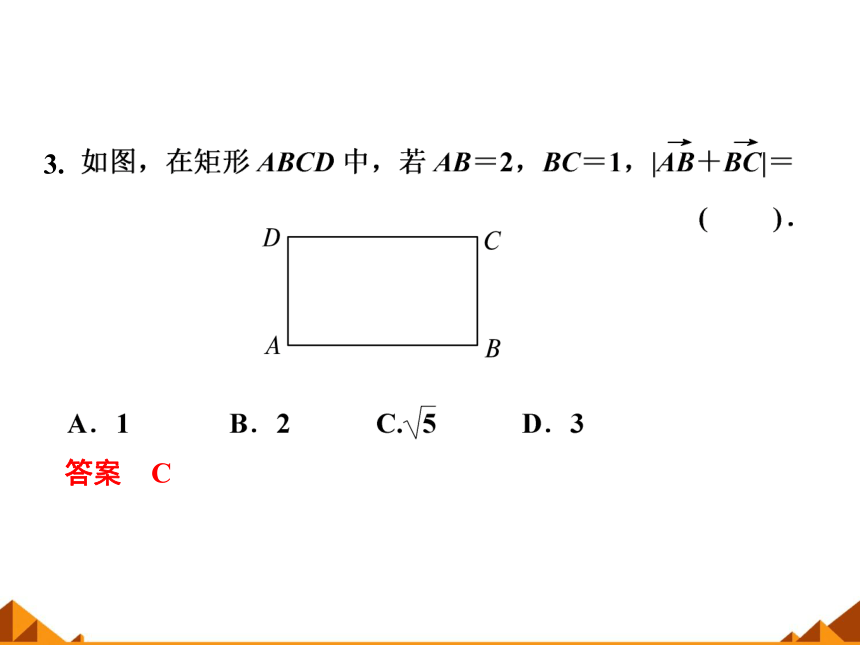
3.
答案 C
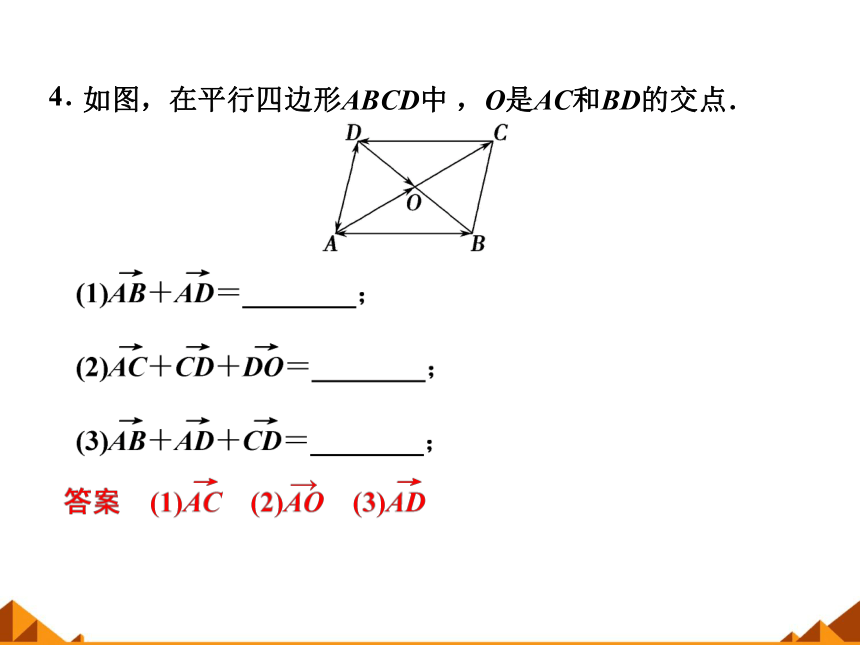
如图,在平行四边形ABCD中 ,O是AC和BD的交点.
4.
准确理解向量加法的三角形法则和平行四边形法则
(1)两个法则的使用条件不同.
三角形法则适用于任意两个非零向量求和,平行四边形法则只适用于两个不共线的向量求和.
(2)当两个向量不共线时,两个法则是一致的.
名师点睛
1.
(3)在使用三角形法则时,应注意“首尾连接”;在使用平行四边形法则时应注意和向量与两向量起点相同.
向量加法的多边形法则
2.
有时,我们会遇到多段向量的合成,如果每次都采取平行四边形法则或三角形法则显得较为麻烦,那么是否可以将其加以简化呢?答案是肯定的,实际上,在三角形法则中,一个重要的原则是“首尾相接”,而向量的加法
运算律使得多个向量的和的运算更为简便,在实际操作中只需重复使用三角形法则,便可以得到: +
其几何意义如图所示.
需说明的几点
(1)两个向量的和仍是一个向量.
(2)当两个非零向量a与b不共线时,a+b的方向与a、b的方向都不相同,且|a+b|<|a|+|b|(三角形两边之和总大于第三边).
(3)当非零向量a与b同向时,a+b,a,b的方向相同,且|a+b|=|a|+|b|.
向量a+b与非零向量a,b的模及方向的关系
(1)当向量a与b不共线时,a+b的方向与a,b都不相同,且|a+b|<|a|+|b|.
(2)当a与b同向时,a+b,a,b的方向相同,且|a+b|=|a|+|b|.
3.
4.
如图所示,O为正六边形ABCDEF的中心,作出下列向量:
题型一 向量的加法法则
【例1】
典例剖析
点评 求作两个向量的和,一般用三角形法则或平行四边形法则,求作三个或三个以上向量的和,常用“折线法”.即先平移向量,使这些向量首尾相接,再连结第一个向量的起点和最后一个向量的终点,即得其和向量.
1.
如图所示,在平行四边形ABCD的对角线BD的延长线和反向延长线上取点F,E,使BE=DF.
求证:四边形AECF是平行四边形.
题型二 向量加法中的化简与证明问题
【例2】
点评 (1)要注意法则的应用;
(2)要注意有向线段表示的向量相等,说明有向线段所在直线平行或重合且长度相等.
如图,在△ABC中,D、E、F分别是BC、AC、AB的中点,化简下列各式:
2.
如图,在重300 N的物体上拴两根绳子,这两根绳子在铅垂线的两侧,与铅垂线的夹角分别为30°、60°,当整个系统处于平衡状态时,求两根绳子的拉力.
题型三 向量加法的应用
【例3】
一辆汽车在平直公路上向西行驶,车上装着风速计和风向标,测得风向为东偏南30°,风速为4 m/s,这时气象台报告实际风速为2 m/s.试求风的实际方向和汽车的速度大小.
解 依据物理知识,有三对相对速度,汽车对地的速度为v车地,风对车的速度为v风车,风对地的速度为v风地.
风对地的速度可以看成车对地与风对车的速度的合速度,
即v风地=v风车+v车地
3.
误区警示 混淆三角形的四心而出错
【示例】
A.内心 B.外心 C.垂心 D.重心
错解 A
错因分析 由于记不住三角形四心的定义及四心的性质,导致出错.
答案 B
纠错心得 内心是三角形的三条角平分线的交点,内心到三角形各边的距离相等;外心是三角形三条边的垂直平分线的交点,外心到三角形各顶点的距离相等;垂心是三角形的三条高的交点;重心是三角形的三条中线的交点,重心到对边中点的距离是到对应顶点的距离的一半.记住四心的定义及性质是解答此题的关键.解答向量问题有很多地方要用到初中所学的平面几何知识,要注意及时复习.
向量的加法法则源自物理上力的合成,有着深刻的物理背景及其严格的几何图形,它不同于数量的加法.
向量加法三角形法则中,当a与b共线时,a+b体现在“线段”的伸长或缩短;当a与b不共线时,a,b,a+b对应的有向线段围成三角形.平行四边形法则适用于两个不共线的向量.当两个向量不共线时,三角形法则与平行四边形法则是一致的,在处理不同问题时,各有其优势.
向量的加法满足交换律和结合律.
课堂总结
1.
2.
3.
边形法则作向量的和向量.
2.掌握向量加法的运算律,能熟练地运用它们进行向量
运算.
向量的加法
向量加法的定义
求________的运算,叫做向量的加法.
向量加法的运算法则
(1)三角形法则
自学导引
1.
2.
向量的和
叫做a与b的和(或和向量),记作_____,即a+b=
.上述求两个向量和的作图法则,叫做向量求和的三角形法则.对于零向量与任一向量a的和有a +0 =__ +_=_.
(2)平行四边形法则
a+b
0
a
a
以___,___为邻边作__________,则对角线上的向量
AB
AD
平行四边形
=a+b,如图所示.这个法则叫做两个向量求和的平行四边形法则.
向量加法的运算律
(1)交换律:a+b=____.
(2)结合律:(____)+c=a+(____).
(3)当a与b反向时,若|a|≥|b|,则a+b与a的方向____,且
|a+b|=______.
若|a|<|b|,则a+b与_的方向相同,且|a+b|=______.
3.
b+a
a+b
b+c
相同
|a|-|b|
b
|b|-|a|
用向量加法的三角形法则和平行四边形法则求a+b,所得的结果一样吗?为什么?
提示 所得结果完全一样.
理由是,在如图的三角形法则中所得的三角形ABC与四边形法则所得的平行四边形ABCD中的三角形ABC是全等的.
自主探究
在△ABC中,下列运算正确的是 ( ).
预习测评
1.
答案 D
已知向量a表示“向东航行1 km”,向量b表示“向南航行1 km”,则a+b表示 ( ).
2.
答案 A
3.
答案 C
如图,在平行四边形ABCD中 ,O是AC和BD的交点.
4.
准确理解向量加法的三角形法则和平行四边形法则
(1)两个法则的使用条件不同.
三角形法则适用于任意两个非零向量求和,平行四边形法则只适用于两个不共线的向量求和.
(2)当两个向量不共线时,两个法则是一致的.
名师点睛
1.
(3)在使用三角形法则时,应注意“首尾连接”;在使用平行四边形法则时应注意和向量与两向量起点相同.
向量加法的多边形法则
2.
有时,我们会遇到多段向量的合成,如果每次都采取平行四边形法则或三角形法则显得较为麻烦,那么是否可以将其加以简化呢?答案是肯定的,实际上,在三角形法则中,一个重要的原则是“首尾相接”,而向量的加法
运算律使得多个向量的和的运算更为简便,在实际操作中只需重复使用三角形法则,便可以得到: +
其几何意义如图所示.
需说明的几点
(1)两个向量的和仍是一个向量.
(2)当两个非零向量a与b不共线时,a+b的方向与a、b的方向都不相同,且|a+b|<|a|+|b|(三角形两边之和总大于第三边).
(3)当非零向量a与b同向时,a+b,a,b的方向相同,且|a+b|=|a|+|b|.
向量a+b与非零向量a,b的模及方向的关系
(1)当向量a与b不共线时,a+b的方向与a,b都不相同,且|a+b|<|a|+|b|.
(2)当a与b同向时,a+b,a,b的方向相同,且|a+b|=|a|+|b|.
3.
4.
如图所示,O为正六边形ABCDEF的中心,作出下列向量:
题型一 向量的加法法则
【例1】
典例剖析
点评 求作两个向量的和,一般用三角形法则或平行四边形法则,求作三个或三个以上向量的和,常用“折线法”.即先平移向量,使这些向量首尾相接,再连结第一个向量的起点和最后一个向量的终点,即得其和向量.
1.
如图所示,在平行四边形ABCD的对角线BD的延长线和反向延长线上取点F,E,使BE=DF.
求证:四边形AECF是平行四边形.
题型二 向量加法中的化简与证明问题
【例2】
点评 (1)要注意法则的应用;
(2)要注意有向线段表示的向量相等,说明有向线段所在直线平行或重合且长度相等.
如图,在△ABC中,D、E、F分别是BC、AC、AB的中点,化简下列各式:
2.
如图,在重300 N的物体上拴两根绳子,这两根绳子在铅垂线的两侧,与铅垂线的夹角分别为30°、60°,当整个系统处于平衡状态时,求两根绳子的拉力.
题型三 向量加法的应用
【例3】
一辆汽车在平直公路上向西行驶,车上装着风速计和风向标,测得风向为东偏南30°,风速为4 m/s,这时气象台报告实际风速为2 m/s.试求风的实际方向和汽车的速度大小.
解 依据物理知识,有三对相对速度,汽车对地的速度为v车地,风对车的速度为v风车,风对地的速度为v风地.
风对地的速度可以看成车对地与风对车的速度的合速度,
即v风地=v风车+v车地
3.
误区警示 混淆三角形的四心而出错
【示例】
A.内心 B.外心 C.垂心 D.重心
错解 A
错因分析 由于记不住三角形四心的定义及四心的性质,导致出错.
答案 B
纠错心得 内心是三角形的三条角平分线的交点,内心到三角形各边的距离相等;外心是三角形三条边的垂直平分线的交点,外心到三角形各顶点的距离相等;垂心是三角形的三条高的交点;重心是三角形的三条中线的交点,重心到对边中点的距离是到对应顶点的距离的一半.记住四心的定义及性质是解答此题的关键.解答向量问题有很多地方要用到初中所学的平面几何知识,要注意及时复习.
向量的加法法则源自物理上力的合成,有着深刻的物理背景及其严格的几何图形,它不同于数量的加法.
向量加法三角形法则中,当a与b共线时,a+b体现在“线段”的伸长或缩短;当a与b不共线时,a,b,a+b对应的有向线段围成三角形.平行四边形法则适用于两个不共线的向量.当两个向量不共线时,三角形法则与平行四边形法则是一致的,在处理不同问题时,各有其优势.
向量的加法满足交换律和结合律.
课堂总结
1.
2.
3.
