4.5.1向量的数量积_课件1-湘教版必修2(21张PPT)
文档属性
| 名称 | 4.5.1向量的数量积_课件1-湘教版必修2(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 394.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览








文档简介
向量的数量积
[学习目标]
1.理解向量数量积的含义及其物理意义,体会向量数量积与向量投影的关系.
2.能正确熟练地应用向量数量积的定义、运算律进行运算.
[知识链接]
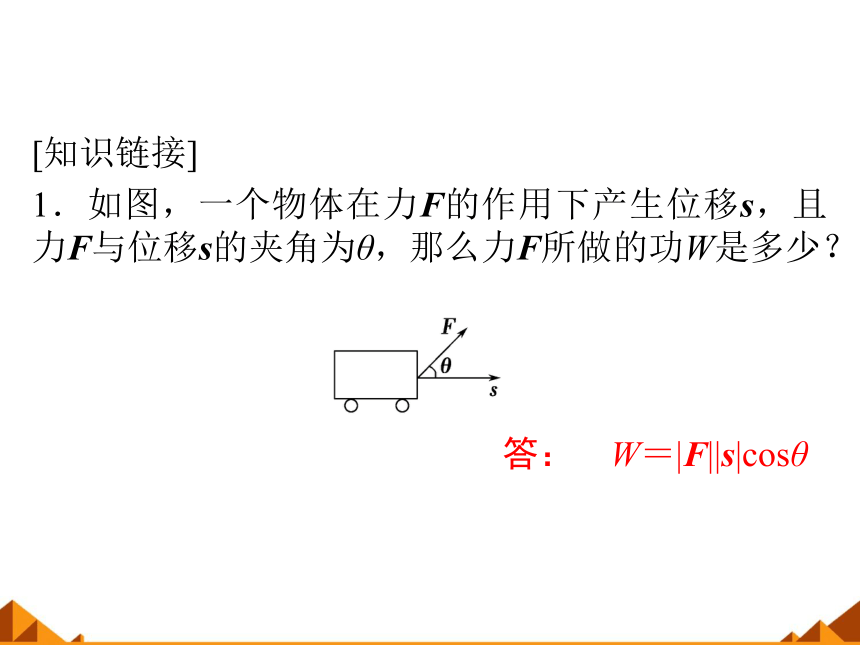
1.如图,一个物体在力F的作用下产生位移s,且力F与位移s的夹角为θ,那么力F所做的功W是多少?
答: W=|F||s|cosθ
2.向量的数量积与数乘向量的区别是什么?
答:向量的数量积a·b是一个实数,不考虑方向;数乘向量λa是一个向量,既有大小,又有方向.
[预习导引]
1.两个向量的夹角规定〈a,b〉为a,b之间所夹的 的 角,取值范围规定为 .
2.向量的数量积(内积)定义|a||b|cos〈a,b〉叫做向量a和b的数量积(或内积),记作a·b.即a·b=|a||b|cos〈a,b〉.
最小
非负
[0,π]
3.定理5:数量积的运算律
(1)交换律:a·b=b ·a,对任意向量a,b成立;
(2)与数乘的结合律:λ(a·b)=(λa)·b=a·(λb),对任意向量a,b和实数λ成立;
(3)分配律:(a+a′)·b=a·b+a′·b,对任意向量a,a′,b成立.
要点一 平面向量数量积的基本概念
例1 下列判断:①若a2+b2=0,则a=b=0;②已知a,b,c是三个非零向量,若a+b=0,则|a·c|=|b·c|;③a,b共线?a·b=|a||b|;④|a||b|0,则a与b的夹角为锐角;⑧若a,b的夹角为θ,则|b|cos θ表示向量b在向量a方向上的投影长.其中正确的是________.
答案 ①②⑥
解析 由于a2≥0,b2≥0,所以,若a2+b2=0,则a=b=0,故①正确;若a+b=0,则a=-b,又a,b,c是三个非零向量,所以a·c=-b·c,所以|a·c|=|b·c|,②正确;a,b共线?a·b=±|a||b|,所以③错.对于④,应有|a||b|≥a·b,所以④错;对于⑤,应该是a·a·a=|a|2a,所以⑤错;a2+b2≥2|a||b|≥2a·b,故⑥正确;当a与b的夹角为0°时,也有a·b>0,因此⑦错;|b|cos θ表示向量b在向量a方向上的投影的数量,而非投影长,故⑧错.
综上可知①②⑥正确.
规律方法 对于这类概念、性质、运算律的问题的解答,关键是要对相关知识深刻理解.特别是那些易与实数运算相混淆的运算律,如消去律、乘法结合律等,当然还有如向量的数量积中有关角的概念以及数量积的性质等.
跟踪演练1 已知a、b、c是三个非零向量,则下列问题中真命题的个数为 ( )
①a·b=±|a|·|b|?a∥b;
②a、b反向?a·b=-|a|·|b|;
③a⊥b?|a+b|=|a-b|;
④|a|=|b|?|a·c|=|b·c|.
A.1 B.2 C.3 D.4
答案 C
解析 ①∵a·b=|a||b|cos θ,∴由a·b=±|a||b|及a、b为非零向量可得cos θ=±1,∴θ=0或π.∴a∥b,且以上各步均可逆,故命题①是真命题.②若a、b反向,则a、b的夹角为π,∴a·b=|a||b|·cos π=-|a||b|,且以上各步均可逆,故命题②是真命题.③当a⊥b时,将向量a、b的起点确定在同一点,则以向量a、b为邻边作平行四边形,则该平行四边形必为矩形,于是它的两条对角线长相等,即有|a+b|=|a-b|.反过来,若|a+b|=|a-b|,则以a、b为邻边的四边形为矩形,∴a⊥b,故命题③是真命题.④当|a|=|b|,但a与c的夹角和b与c的夹角不等时,就有|a·c|≠|b·c|,反过来由|a·c|=|b·c|也推不出|a|=|b|.故命题④是假命题.
综上,在四个命题中,前3个是真命题,第4个是假命题.
要点二 平面向量数量积的基本运算
例2 已知|a|=3,|b|=6,当①a∥b,②a与b的夹角是60°时,分别求a·b.
解 ①当a∥b时,
若a与b同向,则它们的夹角θ=0°,
∴a·b=|a||b|cos 0°=3×6×1=18;
规律方法 非零向量共线的充要条件是a·b=±|a|·|b|,因此,当a∥b时,有0°或180°两种可能.
若a与b反向,则它们的夹角θ=180°,
∴a·b=|a||b|cos 180°=3×6×(-1)=-18;
②当a与b的夹角是60°时,有a·b=|a||b|cos 60°=3×6×=9.
跟踪演练2 若向量a、b、c满足a+b+c=0,且|a|=3,|b|=1,|c|=4,求a·b+b·c+c·a.
解 法一 由已知得|c|=|a|+|b|,c=-a-b,
向量a与b同向,而向量c与它们反向.
∴a·b+b·c+c·a=3cos 0°+4cos 180°+
12cos 180°=3-4-12=-13.
法二 ∵(a+b+c)2=a2+b2+c2+2(a·b+b·c+c·a),
∴a·b+b·c+c·a===-13.
答案 C
2.若向量a,b满足|a|=|b|=1,a与b的夹角为120°,则a·a+a·b=________.
答案 -25
1.两向量a与b的数量积是一个实数,不是一个向量,其值可以为正(当a≠0,b≠0,0°≤θ<90°时),也可以为负(当a≠0,b≠0,90°<θ≤180°时),还可以为0(当a=0或b=0或θ=90°时).
2.两个向量的数量积是两个向量之间的一种运算,与实数乘实数、实数乘向量的乘法运算是有区别的,在书写时一定要把它们严格区分开来,绝不可混淆.
再见
[学习目标]
1.理解向量数量积的含义及其物理意义,体会向量数量积与向量投影的关系.
2.能正确熟练地应用向量数量积的定义、运算律进行运算.
[知识链接]
1.如图,一个物体在力F的作用下产生位移s,且力F与位移s的夹角为θ,那么力F所做的功W是多少?
答: W=|F||s|cosθ
2.向量的数量积与数乘向量的区别是什么?
答:向量的数量积a·b是一个实数,不考虑方向;数乘向量λa是一个向量,既有大小,又有方向.
[预习导引]
1.两个向量的夹角规定〈a,b〉为a,b之间所夹的 的 角,取值范围规定为 .
2.向量的数量积(内积)定义|a||b|cos〈a,b〉叫做向量a和b的数量积(或内积),记作a·b.即a·b=|a||b|cos〈a,b〉.
最小
非负
[0,π]
3.定理5:数量积的运算律
(1)交换律:a·b=b ·a,对任意向量a,b成立;
(2)与数乘的结合律:λ(a·b)=(λa)·b=a·(λb),对任意向量a,b和实数λ成立;
(3)分配律:(a+a′)·b=a·b+a′·b,对任意向量a,a′,b成立.
要点一 平面向量数量积的基本概念
例1 下列判断:①若a2+b2=0,则a=b=0;②已知a,b,c是三个非零向量,若a+b=0,则|a·c|=|b·c|;③a,b共线?a·b=|a||b|;④|a||b|
答案 ①②⑥
解析 由于a2≥0,b2≥0,所以,若a2+b2=0,则a=b=0,故①正确;若a+b=0,则a=-b,又a,b,c是三个非零向量,所以a·c=-b·c,所以|a·c|=|b·c|,②正确;a,b共线?a·b=±|a||b|,所以③错.对于④,应有|a||b|≥a·b,所以④错;对于⑤,应该是a·a·a=|a|2a,所以⑤错;a2+b2≥2|a||b|≥2a·b,故⑥正确;当a与b的夹角为0°时,也有a·b>0,因此⑦错;|b|cos θ表示向量b在向量a方向上的投影的数量,而非投影长,故⑧错.
综上可知①②⑥正确.
规律方法 对于这类概念、性质、运算律的问题的解答,关键是要对相关知识深刻理解.特别是那些易与实数运算相混淆的运算律,如消去律、乘法结合律等,当然还有如向量的数量积中有关角的概念以及数量积的性质等.
跟踪演练1 已知a、b、c是三个非零向量,则下列问题中真命题的个数为 ( )
①a·b=±|a|·|b|?a∥b;
②a、b反向?a·b=-|a|·|b|;
③a⊥b?|a+b|=|a-b|;
④|a|=|b|?|a·c|=|b·c|.
A.1 B.2 C.3 D.4
答案 C
解析 ①∵a·b=|a||b|cos θ,∴由a·b=±|a||b|及a、b为非零向量可得cos θ=±1,∴θ=0或π.∴a∥b,且以上各步均可逆,故命题①是真命题.②若a、b反向,则a、b的夹角为π,∴a·b=|a||b|·cos π=-|a||b|,且以上各步均可逆,故命题②是真命题.③当a⊥b时,将向量a、b的起点确定在同一点,则以向量a、b为邻边作平行四边形,则该平行四边形必为矩形,于是它的两条对角线长相等,即有|a+b|=|a-b|.反过来,若|a+b|=|a-b|,则以a、b为邻边的四边形为矩形,∴a⊥b,故命题③是真命题.④当|a|=|b|,但a与c的夹角和b与c的夹角不等时,就有|a·c|≠|b·c|,反过来由|a·c|=|b·c|也推不出|a|=|b|.故命题④是假命题.
综上,在四个命题中,前3个是真命题,第4个是假命题.
要点二 平面向量数量积的基本运算
例2 已知|a|=3,|b|=6,当①a∥b,②a与b的夹角是60°时,分别求a·b.
解 ①当a∥b时,
若a与b同向,则它们的夹角θ=0°,
∴a·b=|a||b|cos 0°=3×6×1=18;
规律方法 非零向量共线的充要条件是a·b=±|a|·|b|,因此,当a∥b时,有0°或180°两种可能.
若a与b反向,则它们的夹角θ=180°,
∴a·b=|a||b|cos 180°=3×6×(-1)=-18;
②当a与b的夹角是60°时,有a·b=|a||b|cos 60°=3×6×=9.
跟踪演练2 若向量a、b、c满足a+b+c=0,且|a|=3,|b|=1,|c|=4,求a·b+b·c+c·a.
解 法一 由已知得|c|=|a|+|b|,c=-a-b,
向量a与b同向,而向量c与它们反向.
∴a·b+b·c+c·a=3cos 0°+4cos 180°+
12cos 180°=3-4-12=-13.
法二 ∵(a+b+c)2=a2+b2+c2+2(a·b+b·c+c·a),
∴a·b+b·c+c·a===-13.
答案 C
2.若向量a,b满足|a|=|b|=1,a与b的夹角为120°,则a·a+a·b=________.
答案 -25
1.两向量a与b的数量积是一个实数,不是一个向量,其值可以为正(当a≠0,b≠0,0°≤θ<90°时),也可以为负(当a≠0,b≠0,90°<θ≤180°时),还可以为0(当a=0或b=0或θ=90°时).
2.两个向量的数量积是两个向量之间的一种运算,与实数乘实数、实数乘向量的乘法运算是有区别的,在书写时一定要把它们严格区分开来,绝不可混淆.
再见
