4.5.2利用数量积计算长度和角度_课件1-湘教版必修2(21张PPT)
文档属性
| 名称 | 4.5.2利用数量积计算长度和角度_课件1-湘教版必修2(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 477.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览








文档简介
利用数量积计算长度和角度
[学习目标]
1.掌握利用向量的数量积的性质,求长度和角度,判断两向量是否垂直,了解其几何意义.
2.会利用向量数量积的有关运算进行计算或证明.
[知识链接]
1.向量数乘的运算律有哪些?
答 (1)λ(μa)=(λμ)a.
(2)(λ+μ)a=λa+μa.
(3)λ(a+b)=λa+λb.
特别地,有(-λ)a=-(λa)=λ(-a);
λ(a-b)=λa-λb.
2.向量数量积的运算律有哪些?
答 (1)交换律:a·b=b·a,对任意向量a,b成立;
(2)与数乘的结合律:λ(a·b)=(λa)·b=a·(λb),对任意向量a,b和实数λ成立;
(3)分配律:(a+a′)·b=a·b+a′·b,对任意向量a,a′,b成立.
[预习导引]
1.向量的数量积的性质
(1)如果b是单位向量,则a·b=b·a=|a|cos〈a,b〉.
(2)a·a=|a|2或|a|=(长度公式).
(3)cos〈a,b〉= =(夹角余弦公式).
(4) a·b=0?a⊥b(垂直条件).
(5)|a·b| |a||b|.
(6)(a+b)2=|a|2+2a·b+|b|2.
(7)(a-b)2=|a|2-2a·b+|b|2.
(8)(a+b)·(a-b)=|a|2-|b|2.
≤
要点一 向量模的运算
例1 已知向量a,b满足|a|=13,|b|=19,|a+b|=24,求|a-b|.
要点二 向量夹角的运算
例2 设n和m是两个单位向量,其夹角是60°,求向量a=2m+n与b=2n-3m的夹角.
规律方法 求向量夹角时,应先根据公式把涉及到的量先计算出来再代入公式求角,注意向量夹角的范围是[0,π].
跟踪演练2 已知a,b都是非零向量,且a+3b与7a-5b垂直,a-4b与7a-2b垂直,求a与b的夹角.
要点三 向量垂直应用
例3 已知|a|=3,|b|=4,且a与b不共线,k为何值时,向量a+kb与a-kb互相垂直.
规律方法 向量a,b夹角为锐角的等价条件是a·b>0且a与b不同向共线;a·b夹角为钝角的等价条件是a·b<0且a与b不反向共线;a与b垂直的等价条件是a·b=0.
跟踪演练3 已知e1与e2是两个互相垂直的单位向量,k为何值时,向量e1+ke2与ke1+e2的夹角为锐角?
答案 B
答案 B
3.若非零向量a,b满足|a|=|b|,(2a+b)·b=0,则a与b的夹角为 ( )
A.30° B.60° C.120° D.150°
答案 C
答案 -8或5
1.两向量a与b的数量积是一个实数,不是一个向量,其值可以为正(当a≠0,b≠0,0°≤θ<90°时),也可以为负(当a≠0,b≠0,90°<θ≤180°时),还可以为0(当a=0或b=0或θ=90°时).
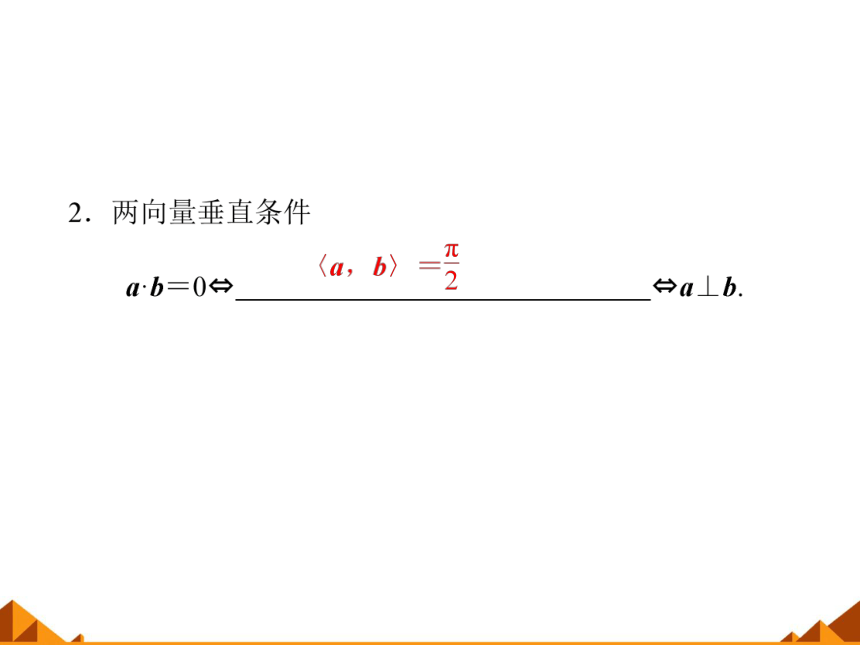
2.两个向量垂直等价于它们的数量积等于0.
3.在实数中,若ab=0则a=0或b=0,但是在数量积中,即使a·b=0,也不能推出a=0或b=0,因为其中cos θ有可能为0.
再见
[学习目标]
1.掌握利用向量的数量积的性质,求长度和角度,判断两向量是否垂直,了解其几何意义.
2.会利用向量数量积的有关运算进行计算或证明.
[知识链接]
1.向量数乘的运算律有哪些?
答 (1)λ(μa)=(λμ)a.
(2)(λ+μ)a=λa+μa.
(3)λ(a+b)=λa+λb.
特别地,有(-λ)a=-(λa)=λ(-a);
λ(a-b)=λa-λb.
2.向量数量积的运算律有哪些?
答 (1)交换律:a·b=b·a,对任意向量a,b成立;
(2)与数乘的结合律:λ(a·b)=(λa)·b=a·(λb),对任意向量a,b和实数λ成立;
(3)分配律:(a+a′)·b=a·b+a′·b,对任意向量a,a′,b成立.
[预习导引]
1.向量的数量积的性质
(1)如果b是单位向量,则a·b=b·a=|a|cos〈a,b〉.
(2)a·a=|a|2或|a|=(长度公式).
(3)cos〈a,b〉= =(夹角余弦公式).
(4) a·b=0?a⊥b(垂直条件).
(5)|a·b| |a||b|.
(6)(a+b)2=|a|2+2a·b+|b|2.
(7)(a-b)2=|a|2-2a·b+|b|2.
(8)(a+b)·(a-b)=|a|2-|b|2.
≤
要点一 向量模的运算
例1 已知向量a,b满足|a|=13,|b|=19,|a+b|=24,求|a-b|.
要点二 向量夹角的运算
例2 设n和m是两个单位向量,其夹角是60°,求向量a=2m+n与b=2n-3m的夹角.
规律方法 求向量夹角时,应先根据公式把涉及到的量先计算出来再代入公式求角,注意向量夹角的范围是[0,π].
跟踪演练2 已知a,b都是非零向量,且a+3b与7a-5b垂直,a-4b与7a-2b垂直,求a与b的夹角.
要点三 向量垂直应用
例3 已知|a|=3,|b|=4,且a与b不共线,k为何值时,向量a+kb与a-kb互相垂直.
规律方法 向量a,b夹角为锐角的等价条件是a·b>0且a与b不同向共线;a·b夹角为钝角的等价条件是a·b<0且a与b不反向共线;a与b垂直的等价条件是a·b=0.
跟踪演练3 已知e1与e2是两个互相垂直的单位向量,k为何值时,向量e1+ke2与ke1+e2的夹角为锐角?
答案 B
答案 B
3.若非零向量a,b满足|a|=|b|,(2a+b)·b=0,则a与b的夹角为 ( )
A.30° B.60° C.120° D.150°
答案 C
答案 -8或5
1.两向量a与b的数量积是一个实数,不是一个向量,其值可以为正(当a≠0,b≠0,0°≤θ<90°时),也可以为负(当a≠0,b≠0,90°<θ≤180°时),还可以为0(当a=0或b=0或θ=90°时).
2.两个向量垂直等价于它们的数量积等于0.
3.在实数中,若ab=0则a=0或b=0,但是在数量积中,即使a·b=0,也不能推出a=0或b=0,因为其中cos θ有可能为0.
再见
