4.6向量的应用_课件1-湘教版必修2(37张PPT)
文档属性
| 名称 | 4.6向量的应用_课件1-湘教版必修2(37张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 576.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览









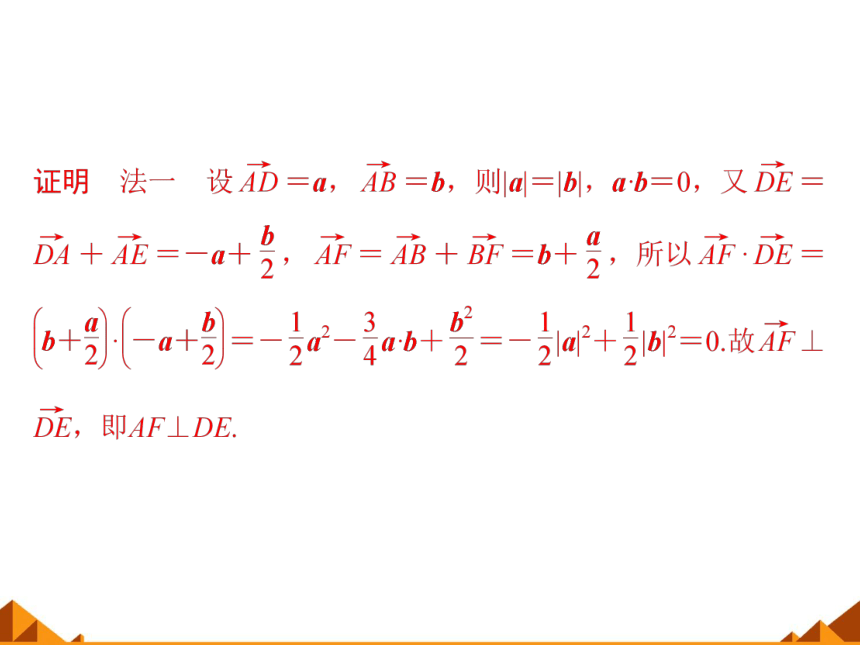


文档简介
向量的应用
[学习目标]
1.能运用向量的知识解决一些简单的平面几何问题.
2.掌握两种基本方法—选择基向量法和坐标建系法.
3.能用向量知识处理一些简单的物理问题.
[知识链接]
1.向量可以解决哪些常见的几何问题?
答:(1)解决直线平行、垂直、线段相等、三点共线、三线共点等位置关系.
(2)解决有关夹角、长度及参数的值等的计算或度量问题.
2.用向量方法解决平面几何问题的“三步曲”是怎样的?
答:(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系,距离,夹角等问题;
(3)把运算结果“翻译”成几何关系.
3.向量的运算与速度、加速度与位移有什么联系?
答:速度、加速度与位移的合成与分解,实质上是向量的加减法运算,而运动的叠加也用到向量的合成, 向量有丰富的物理背景.向量源于物理中的力、速度、加速度、位移等“矢量”;向量在解决涉及上述物理量的合成与分解时,实质就是向量的线性运算.
x1y2-x2y1=0
x1x2+y1y2=0
2.向量方法在物理中的应用
(1)力、速度、加速度、位移都是 .
(2)力、速度、加速度、位移的合成与分解就是向量的 运算,运动的叠加亦用到向量的合成.
(3)动量mv是 .
(4)功即是力F与所产生位移s的 .
向量
加、减
数乘向量
数量积
要点一 平面几何中的垂直问题
例1 如图所示,在正方形ABCD中,E,F分别是AB,BC的中点,求证:AF⊥DE.
规律方法 对于线段的垂直问题,可以联想到两个向量垂直的条件(向量的数量积为0),而对于这一条件的应用,可以考虑向量关系式的形式,也可以考虑坐标的形式.
要点二 平面几何中的长度问题
例2 如图所示,四边形ABCD是正方形,BE∥AC,AC=CE,EC的延长线交BA的延长线于F.求证:AF=AE.
跟踪演练2 如图,平行四边形ABCD中,已知AD=1,AB=2,对角线BD=2,求对角线AC的长.
要点三 向量的线性运算在物理中的应用
例3 帆船比赛是借助风帆推动船只在规定距离内竞速的一项水上运动,如果一帆船所受的风力方向为北偏东30°,速度为20 km/h,此时水的流向是正东,流速为20 km/h.若不考虑其他因素,求帆船的速度与方向.
解 建立如图所示的直角坐标系,风的方向为北偏东30°,
要点四 向量的数量积在物理中的应用
例4 如图,质量m=2.0 kg的木块,在平行于斜面向上的拉力F=10 N的作用下,沿倾斜角θ=30°的光滑斜面向上滑行|s|=2.0 m的距离.
(1)分别求物体所受各力在这一过程中对
物体做的功;
(2)在这一过程中,物体所受各力对物体
做的功的代数和是多少?
(3)求物体所受合外力对物体所做的功,并指出它与物体所受各个力对物体做功的代数和之间有什么关系.
解 (1)木块共受三个力的作用,重力G,拉力F和支持力F1,如题图所示,拉力F与位移s方向相同,所以拉力对木块所做的功为:
WF=F·s=|F||s|cos θ=20(J).
支持力F1与位移方向垂直,不做功,即W1=F1·s=0.
重力G对物体所做的功为:
WG=G·s=|G||s|cos(90°+θ)=-19.6(J).
(2)物体所受各力对物体做功的代数和为:
W=WF+WN+WG=20+0-19.6=0.4(J).
(3)物体所受合外力的大小为:
|F合|=|F|-|G|sin 30°=0.2(N).
∴合外力对物体所做的功为:
W=F合·s=0.2×2=0.4(J).
∴物体所受合外力对物体所做的功与物体所受各力对物体做功的代数和相等.
规律方法 解决力学有关问题,做好正确的受力分析是数学建模的基础.要认真体会用向量方法解决物理问题和解释物理现象的方法.
跟踪演练4 已知两恒力F1=(3,4)、F2=(6,-5)作用于同一质点,使之由点A(20,15)移动到点B(7,0),试求:
(1)F1、F2分别对质点所做的功;(2)F1,F2的合力F为质点所做的功.
A.直角三角形 B.等腰三角形
C.等边三角形 D.等腰直角三角形
答案 B
答案 D
3.正方形OABC的边长为1,点D、E分别为AB,BC的中点,试求cos∠DOE的值.
解 因为a·b=b·c,所以(a-c)·b=0,而由向量加法的三角形法则可知,a+b+c=0,所以b=-a-c,所以(a-c)·(-a-c)=0,即(a-c)·(a+c)=0,得到a2-c2=0,a2=c2,即|a|2=|c|2,也就是|a|=|c|.同理可得,|a|=|b|,所以|a|=|b|=|c|.故三角形ABC是等边三角形.
1.向量的坐标表示简化了向量数量积的运算.为利用向量法解决平面几何问题以及解析几何问题提供了完美的理论依据和有力的工具支持.
2.应用数量积运算可以解决两向量的垂直、平行、夹角以及长度等几何问题,在学习中要不断地提高利用向量工具解决数学问题的能力.
再见
[学习目标]
1.能运用向量的知识解决一些简单的平面几何问题.
2.掌握两种基本方法—选择基向量法和坐标建系法.
3.能用向量知识处理一些简单的物理问题.
[知识链接]
1.向量可以解决哪些常见的几何问题?
答:(1)解决直线平行、垂直、线段相等、三点共线、三线共点等位置关系.
(2)解决有关夹角、长度及参数的值等的计算或度量问题.
2.用向量方法解决平面几何问题的“三步曲”是怎样的?
答:(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系,距离,夹角等问题;
(3)把运算结果“翻译”成几何关系.
3.向量的运算与速度、加速度与位移有什么联系?
答:速度、加速度与位移的合成与分解,实质上是向量的加减法运算,而运动的叠加也用到向量的合成, 向量有丰富的物理背景.向量源于物理中的力、速度、加速度、位移等“矢量”;向量在解决涉及上述物理量的合成与分解时,实质就是向量的线性运算.
x1y2-x2y1=0
x1x2+y1y2=0
2.向量方法在物理中的应用
(1)力、速度、加速度、位移都是 .
(2)力、速度、加速度、位移的合成与分解就是向量的 运算,运动的叠加亦用到向量的合成.
(3)动量mv是 .
(4)功即是力F与所产生位移s的 .
向量
加、减
数乘向量
数量积
要点一 平面几何中的垂直问题
例1 如图所示,在正方形ABCD中,E,F分别是AB,BC的中点,求证:AF⊥DE.
规律方法 对于线段的垂直问题,可以联想到两个向量垂直的条件(向量的数量积为0),而对于这一条件的应用,可以考虑向量关系式的形式,也可以考虑坐标的形式.
要点二 平面几何中的长度问题
例2 如图所示,四边形ABCD是正方形,BE∥AC,AC=CE,EC的延长线交BA的延长线于F.求证:AF=AE.
跟踪演练2 如图,平行四边形ABCD中,已知AD=1,AB=2,对角线BD=2,求对角线AC的长.
要点三 向量的线性运算在物理中的应用
例3 帆船比赛是借助风帆推动船只在规定距离内竞速的一项水上运动,如果一帆船所受的风力方向为北偏东30°,速度为20 km/h,此时水的流向是正东,流速为20 km/h.若不考虑其他因素,求帆船的速度与方向.
解 建立如图所示的直角坐标系,风的方向为北偏东30°,
要点四 向量的数量积在物理中的应用
例4 如图,质量m=2.0 kg的木块,在平行于斜面向上的拉力F=10 N的作用下,沿倾斜角θ=30°的光滑斜面向上滑行|s|=2.0 m的距离.
(1)分别求物体所受各力在这一过程中对
物体做的功;
(2)在这一过程中,物体所受各力对物体
做的功的代数和是多少?
(3)求物体所受合外力对物体所做的功,并指出它与物体所受各个力对物体做功的代数和之间有什么关系.
解 (1)木块共受三个力的作用,重力G,拉力F和支持力F1,如题图所示,拉力F与位移s方向相同,所以拉力对木块所做的功为:
WF=F·s=|F||s|cos θ=20(J).
支持力F1与位移方向垂直,不做功,即W1=F1·s=0.
重力G对物体所做的功为:
WG=G·s=|G||s|cos(90°+θ)=-19.6(J).
(2)物体所受各力对物体做功的代数和为:
W=WF+WN+WG=20+0-19.6=0.4(J).
(3)物体所受合外力的大小为:
|F合|=|F|-|G|sin 30°=0.2(N).
∴合外力对物体所做的功为:
W=F合·s=0.2×2=0.4(J).
∴物体所受合外力对物体所做的功与物体所受各力对物体做功的代数和相等.
规律方法 解决力学有关问题,做好正确的受力分析是数学建模的基础.要认真体会用向量方法解决物理问题和解释物理现象的方法.
跟踪演练4 已知两恒力F1=(3,4)、F2=(6,-5)作用于同一质点,使之由点A(20,15)移动到点B(7,0),试求:
(1)F1、F2分别对质点所做的功;(2)F1,F2的合力F为质点所做的功.
A.直角三角形 B.等腰三角形
C.等边三角形 D.等腰直角三角形
答案 B
答案 D
3.正方形OABC的边长为1,点D、E分别为AB,BC的中点,试求cos∠DOE的值.
解 因为a·b=b·c,所以(a-c)·b=0,而由向量加法的三角形法则可知,a+b+c=0,所以b=-a-c,所以(a-c)·(-a-c)=0,即(a-c)·(a+c)=0,得到a2-c2=0,a2=c2,即|a|2=|c|2,也就是|a|=|c|.同理可得,|a|=|b|,所以|a|=|b|=|c|.故三角形ABC是等边三角形.
1.向量的坐标表示简化了向量数量积的运算.为利用向量法解决平面几何问题以及解析几何问题提供了完美的理论依据和有力的工具支持.
2.应用数量积运算可以解决两向量的垂直、平行、夹角以及长度等几何问题,在学习中要不断地提高利用向量工具解决数学问题的能力.
再见
