5.1.1两角和与差的正弦和余弦课件-湘教版必修2(19张PPT)
文档属性
| 名称 | 5.1.1两角和与差的正弦和余弦课件-湘教版必修2(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 517.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览





文档简介
5.1.1 两角和与差的
正弦和余弦
创设情境
=
?
思考:
1.我们已经知道 等特殊角的三角函数值,那能否
通过角的关系(不査表)求得 角的余弦值?
2.实数乘法满足分配律 ,下列成立吗?
≠
创设情境
如何用 , 的正弦、余弦值来表示 呢?
思考:
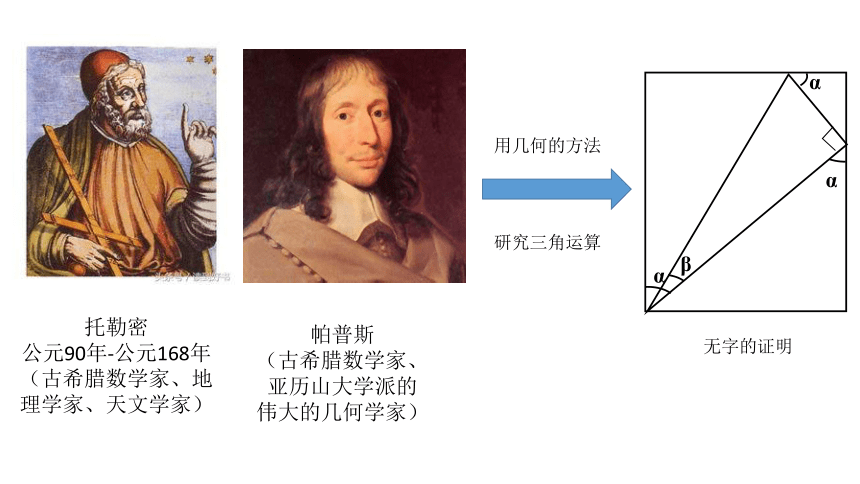
托勒密
公元90年-公元168年
(古希腊数学家、地理学家、天文学家)
帕普斯
(古希腊数学家、亚历山大学派的伟大的几何学家)
用几何的方法
研究三角运算
无字的证明
β
α
α
α
∟
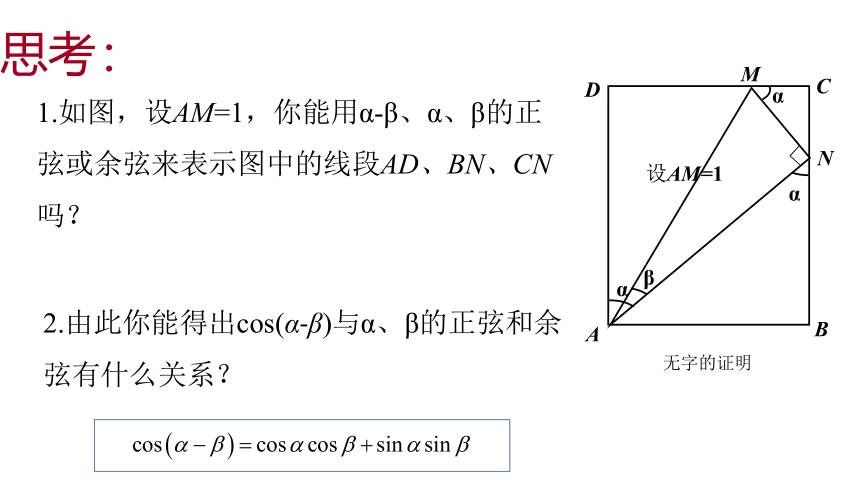
1.如图,设AM=1,你能用α-β、α、β的正弦或余弦来表示图中的线段AD、BN、CN吗?
思考:
设AM=1
β
α
α
α
无字的证明
M
N
A
B
C
D
∟
2.由此你能得出cos(α-β)与α、β的正弦和余弦有什么关系?
探究新知
探究
上述公式由于几何图形的限制,角α、β都是锐角且α>β,那么这一结论是否对任意的α、β都成立呢?因此,我们有必要寻找一个新的视角解决此问题。
观察公式 cos(α-β)= cosαcosβ+sinαsinβ 左右两端的结构, 你能联想到最近学习的什么运算?
复习回顾
1、数量积的定义: ;
2、数量积的坐标表示:若 , ,则
;
3、夹角余弦公式: .
探究新知
如图,A、B分别为角α、β 的终边与单位圆上的交点, 则
(1) ;
;
(2) ;
(3) ;
;
α
β
(4) .
θ
B
A
y
x
o
β的终边
α的终边
θ
B
A
y
x
o
α的终边
β的终边
θ=α-β+2kπ,
θ=β-α+2kπ,
对于任意角α、β都有 .所以
新知探究
cos(α-β)= cosαcosβ+sinαsinβ
对于任意角α、β都有
已知两个角α,β的正弦,余弦sin α,sin β cosα,cos β,求α+β的余弦。
思考:
cos(α+β)= cosαcosβ-sinαsinβ
cos(α-β)= cosαcosβ+sinαsinβ (差角余弦公式)
cos(α+β)= cosαcosβ-sinαsinβ (和角余弦公式)
两角和与差的余弦公式:
我们将和角余弦公式简记为C(α+β) ,差角余弦公式简记为C(α+β) ,以便于记忆和应用。
公式有怎样的结构特征?
例1 求15°,75°的余弦值.
例2 求下列式子的值:
.
例3 已知 ,求 ,
的值。
分析 要利用和差角余弦公式求 , ,
需要先求出
解 由于 ,故
变式应用
变式 已知 ,求 的值。
解 由于 且 ,故 在第二
象限,
知识小结
小结
方法、思想小结
01
两角和与差的余弦公式:
01
02
cos(α-β)= cosαcosβ+sinαsinβ
cos(α+β)= cosαcosβ-sinαsinβ
用已知角表示未知角:如????=????+?????????, 2????=????+????+?????????等。
?
特殊到一般、类比等;
作业
1.教材132页:
(1)(2) 2. (1) 3. (1) 12题
2.思考题:
探究两角和与差的正弦公式。
2019
谢谢!
正弦和余弦
创设情境
=
?
思考:
1.我们已经知道 等特殊角的三角函数值,那能否
通过角的关系(不査表)求得 角的余弦值?
2.实数乘法满足分配律 ,下列成立吗?
≠
创设情境
如何用 , 的正弦、余弦值来表示 呢?
思考:
托勒密
公元90年-公元168年
(古希腊数学家、地理学家、天文学家)
帕普斯
(古希腊数学家、亚历山大学派的伟大的几何学家)
用几何的方法
研究三角运算
无字的证明
β
α
α
α
∟
1.如图,设AM=1,你能用α-β、α、β的正弦或余弦来表示图中的线段AD、BN、CN吗?
思考:
设AM=1
β
α
α
α
无字的证明
M
N
A
B
C
D
∟
2.由此你能得出cos(α-β)与α、β的正弦和余弦有什么关系?
探究新知
探究
上述公式由于几何图形的限制,角α、β都是锐角且α>β,那么这一结论是否对任意的α、β都成立呢?因此,我们有必要寻找一个新的视角解决此问题。
观察公式 cos(α-β)= cosαcosβ+sinαsinβ 左右两端的结构, 你能联想到最近学习的什么运算?
复习回顾
1、数量积的定义: ;
2、数量积的坐标表示:若 , ,则
;
3、夹角余弦公式: .
探究新知
如图,A、B分别为角α、β 的终边与单位圆上的交点, 则
(1) ;
;
(2) ;
(3) ;
;
α
β
(4) .
θ
B
A
y
x
o
β的终边
α的终边
θ
B
A
y
x
o
α的终边
β的终边
θ=α-β+2kπ,
θ=β-α+2kπ,
对于任意角α、β都有 .所以
新知探究
cos(α-β)= cosαcosβ+sinαsinβ
对于任意角α、β都有
已知两个角α,β的正弦,余弦sin α,sin β cosα,cos β,求α+β的余弦。
思考:
cos(α+β)= cosαcosβ-sinαsinβ
cos(α-β)= cosαcosβ+sinαsinβ (差角余弦公式)
cos(α+β)= cosαcosβ-sinαsinβ (和角余弦公式)
两角和与差的余弦公式:
我们将和角余弦公式简记为C(α+β) ,差角余弦公式简记为C(α+β) ,以便于记忆和应用。
公式有怎样的结构特征?
例1 求15°,75°的余弦值.
例2 求下列式子的值:
.
例3 已知 ,求 ,
的值。
分析 要利用和差角余弦公式求 , ,
需要先求出
解 由于 ,故
变式应用
变式 已知 ,求 的值。
解 由于 且 ,故 在第二
象限,
知识小结
小结
方法、思想小结
01
两角和与差的余弦公式:
01
02
cos(α-β)= cosαcosβ+sinαsinβ
cos(α+β)= cosαcosβ-sinαsinβ
用已知角表示未知角:如????=????+?????????, 2????=????+????+?????????等。
?
特殊到一般、类比等;
作业
1.教材132页:
(1)(2) 2. (1) 3. (1) 12题
2.思考题:
探究两角和与差的正弦公式。
2019
谢谢!
