黑龙江省哈尔滨市中学2020-2021学年高二下学期期末考试理科数学试题 Word版含答案
文档属性
| 名称 | 黑龙江省哈尔滨市中学2020-2021学年高二下学期期末考试理科数学试题 Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 490.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 20:26:27 | ||
图片预览



文档简介
哈尔滨中学2020-2021学年度下学期期末
学业阶段性评价考试高二学年数学学科试卷(理科)
(考试时间:120分钟
满分:150分)
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只
有一项是符合题目要求的,请将答案填涂在客观题答题卡.上。
1.命题“,”的否定是(
)
A.,
B.,
C.,
D.不存在,
2.设随机变量服从正态分布,若,则的值为(
)
A.0.2
B.0.3
C.0.4
D.0.6
3.已知离散型随机变量的分布列如表所示,则常数为(
)
0
1
A.
B.
C.或
D.
4.每年新春佳节时,我国许多地区的人们有贴窗花的习俗,以此达到装点环境、渲染气氛的目的,并寄托着辞旧迎新、接福纳祥的愿望.如图是一张“春到福来”的剪纸窗花,为了估计深色部分的面积,将窗花图案放置在边长为20cm的正方形内,在该正方形内随机生成1000个点,恰有535个点落在深色区域内,则此窗花图案中深色区域的面积约为(
)
A.
B.
C.
D.
5.设,,那么是的(
)
A.充分不必要条件
B.必要不充分条件
C.必要条件
D.既不充分也不必要条件
6.掷一枚硬币两次,记事件“第一次出现正面”,“第二次出现反面”,下列结论正确的为(
)
A.
B.
C.与互斥
D.与相互独立
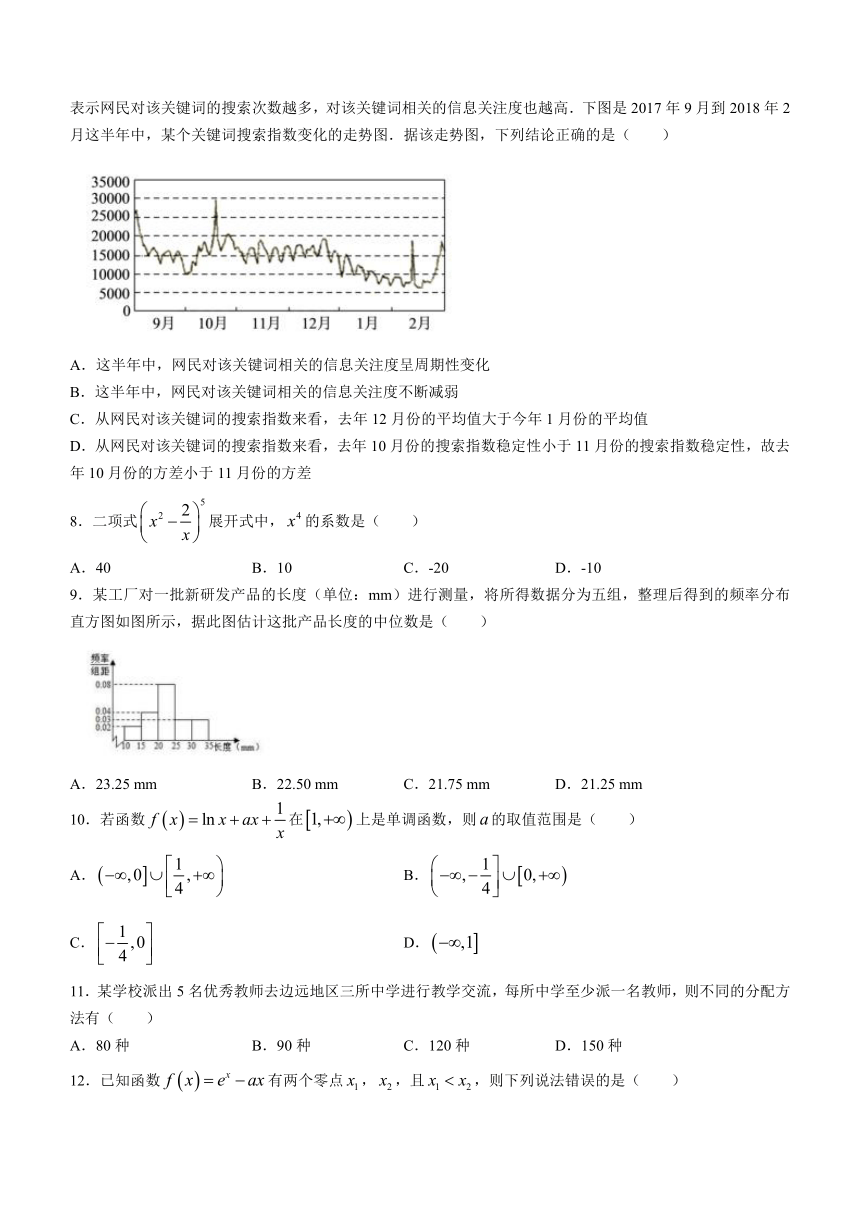
7.“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词搜索指数变化的走势图.据该走势图,下列结论正确的是(
)
A.这半年中,网民对该关键词相关的信息关注度呈周期性变化
B.这半年中,网民对该关键词相关的信息关注度不断减弱
C.从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
D.从网民对该关键词的搜索指数来看,去年10月份的搜索指数稳定性小于11月份的搜索指数稳定性,故去年10月份的方差小于11月份的方差
8.二项式展开式中,的系数是(
)
A.40
B.10
C.-20
D.-10
9.某工厂对一批新研发产品的长度(单位:mm)进行测量,将所得数据分为五组,整理后得到的频率分布直方图如图所示,据此图估计这批产品长度的中位数是(
)
A.23.25
mm
B.22.50
mm
C.21.75
mm
D.21.25
mm
10.若函数在上是单调函数,则的取值范围是(
)
A.
B.
C.
D.
11.某学校派出5名优秀教师去边远地区三所中学进行教学交流,每所中学至少派一名教师,则不同的分配方法有(
)
A.80种
B.90种
C.120种
D.150种
12.已知函数有两个零点,,且,则下列说法错误的是(
)
A.
B.
C.
D.有极小值点,且
二.填空题:本题共4小题,每小题5分,共20分,请将答案写在答题纸指定的位置上。
13.某气象台统计,该地区下雨的概率为,刮四级以上风的概率为,既刮四级以上的风又下雨的概率为,设为下雨,为刮四级以上的风,则______.
14.直线与曲线在第一象限内围成的封闭图形的面积为______.
15.对某种产品的6件不同的正品和4件不同次品一一进行测试,直到区分出所有次品为止。若所有次品恰好在第5次测试被全部发现,则这样的测试方法有______种。
16.下列命题中,正确命题的序号为______.
①已知随机变量服从二项分布,若,,则;
②将一组数据中的每个数据都加上同一个常数后,方差恒不变;
③某厂家声称自己的产品合格率为99%,市场质量管理人员抽取了这个厂家的2件产品进行检验,发现不都合格,由此可知厂家所声称的合格率不可信。
④某人在10次射击中,击中目标的次数为,,则当时概率最大.
三、解答题:本题共6小题,满分70分。解答应写出文字说明、证明过程或演算步骤。
17.(本题满分10分)
张先生家住小区,他在科技园区工作,从家开车到公司上班有,两条路线(如图),路线上有,,三个路口,各路口遇到红灯的均为;上有,两个路口,各路口遇到红灯的概率依次为,.
(1)若走路线,求最多遇到1次红灯的概率;
(2)若走路线,求他遇到红灯的次数的分布列和数学期望.
18.(本题满分12分)
已知某单位甲、乙、丙三个部门员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(2)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.用表示抽取的3人中睡眠不足的员工人数,求随机变量的分布列和数学期望;
19.(本题满分12分)
已知函数,.
(1)若,求曲线在点处的切线方程;
(2)若对于任意,都有成立,求实数的取值范围.
20.(本题满分12分)耐盐碱水稻俗称“海水稻”,是一种可以长在滩涂和盐碱地的水稻,海水稻的灌溉是将海水稀释后进行灌溉,某试验基地为了研究海水浓度对亩产量(吨)的影响,通过在试验田的种植实验,测得了某种海水稻的亩产量与海水浓度的数据如表,绘制散点图发现,可用线性回归模型拟合亩产量与海水浓度之间的相关关系,用最小二乘法计算得与之间的线性回归方程为.
(1)求,并估计当浇灌海水浓度为8时该品种的亩产量;
(2)(i)完成下列残差表:
海水浓度
3
4
5
6
7
亩产量(吨)
0.62
0.58
0.49
0.4
0.31
残差
(ii)统计学中常用相关指数来刻画回归效果,越大,模型拟合效果越好,如假设,就说明预报变量的差异有80%是由解释变量引起的,请计算相关指数(精确到0.01),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的?
附:残差公式,相关指数
21.(本题满分12分)为了解某品种一批树苗生长情况,在该批树苗中随机抽取了容量为120的样本,测量树苗高度(单位:cm),经统计,其高度均在区间内,将其按,,,,,分成6组,制成如图所示的频率分布直方图.其中高度为27cm及以上的树苗为优质树苗.
(1)求图中的值
(2)已知抽取这120棵树苗来自于A,B两个试验区,部分数据如下列联表:
A试验区
B试验区
合计
优质树苗
20
非优质树苗
60
合计
将列联表补充完整,并判断是否有99.9%的把握认为优质树苗与A,B两个试验区有关系,并说明理由;
(3)用样本估计总体,
若从这批树苗中随机抽取4棵,其中优质树苗的棵数为,求的数学期望.
下面的临界值表仅供参考:
0.15
0.10
0.05
0.25
0.01
0.005
0.001
2.702
2.706
3.841
5.024
6.635
7.879
10.828
参考公式:,其中.
22.(本题满分12分)
已知函数,
.
(1)若,求的取值范围;
(2)当时,证明:.
期末数学理答案
1-12
CBABA
DCABB
DC
13.;14.4;15.576;16.②③④.
17.(1)设走路线最多遇到1次红灯为事件,则.
(2)依题意,的可能取值为0,1,2.
则;;
,
随机变量的分布列为:
0
1
2
.
18.(1)由己知,甲、乙、丙三个部门的员工人数之比为3:2:2,由于采用分层抽样的方法从中抽取7人。因此应从甲、乙、两三个部门的员工中分别抽取3人,2人,2人.
(2)随机变量的所有可能取值为0,1,2,3.
.
所以。随机变量的分布列为
0
1
2
3
随机变量的数学期望.
19.(1),,
,则.
所以在点处的切线方程为,即.
(2)因为对于任意,都有成立,所以,
即问题转化为对于恒成立,即
对于恒成立,令,则,
令,,则.所以在区间上单调递增,
故,进而,所以在区间上单调递增,
函数,
要使对于恒成立,只要,所以,即实数的取值范围是.
20.(1)经计算,,,
由可得,,
当时,,所以当海水浓度为8时,该品种的亩产量为0.24吨.
(2)(i)由(1)知,从而有
浓度(千分之)
3
4
5
6
7
亩产量(吨)
0.62
0.58
0.49
0.4
0.31
残差
-0.02
0.02
0.01
0
-0.01
(ii),所以亩产量的变化有98%是由海水引起的.
21.(1)根据直方图数据,有,解得.
(2)根据直方图可知,样本中优质树苗有,列联表如下:
A试验区
B试验区
合计
优质树苗
10
20
30
非优质树苗
60
30
90
合计
70
50
120
可得.
所以,没有99.9%的把握认为优质树苗与A,B两个试验区有关系.
(3)由己知,这批树苗为优质树苗的概率为,且服从二项分布,故数学期望.
22.(1),
当时,.所以函数在上单调递增,所以,满足题意.
当时,,函数在上单调递减,,不符合题意.
当时,令,在存在,使得成立,
所以时,,函数在上单调递减,则,不符合题意.
综上,的取值范围为.
(2)当时,,
要证,即证,即,
设,则
.
由(1)知,又,
所以,所以在上单调递增,故,
所以,,.
学业阶段性评价考试高二学年数学学科试卷(理科)
(考试时间:120分钟
满分:150分)
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只
有一项是符合题目要求的,请将答案填涂在客观题答题卡.上。
1.命题“,”的否定是(
)
A.,
B.,
C.,
D.不存在,
2.设随机变量服从正态分布,若,则的值为(
)
A.0.2
B.0.3
C.0.4
D.0.6
3.已知离散型随机变量的分布列如表所示,则常数为(
)
0
1
A.
B.
C.或
D.
4.每年新春佳节时,我国许多地区的人们有贴窗花的习俗,以此达到装点环境、渲染气氛的目的,并寄托着辞旧迎新、接福纳祥的愿望.如图是一张“春到福来”的剪纸窗花,为了估计深色部分的面积,将窗花图案放置在边长为20cm的正方形内,在该正方形内随机生成1000个点,恰有535个点落在深色区域内,则此窗花图案中深色区域的面积约为(
)
A.
B.
C.
D.
5.设,,那么是的(
)
A.充分不必要条件
B.必要不充分条件
C.必要条件
D.既不充分也不必要条件
6.掷一枚硬币两次,记事件“第一次出现正面”,“第二次出现反面”,下列结论正确的为(
)
A.
B.
C.与互斥
D.与相互独立
7.“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词搜索指数变化的走势图.据该走势图,下列结论正确的是(
)
A.这半年中,网民对该关键词相关的信息关注度呈周期性变化
B.这半年中,网民对该关键词相关的信息关注度不断减弱
C.从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
D.从网民对该关键词的搜索指数来看,去年10月份的搜索指数稳定性小于11月份的搜索指数稳定性,故去年10月份的方差小于11月份的方差
8.二项式展开式中,的系数是(
)
A.40
B.10
C.-20
D.-10
9.某工厂对一批新研发产品的长度(单位:mm)进行测量,将所得数据分为五组,整理后得到的频率分布直方图如图所示,据此图估计这批产品长度的中位数是(
)
A.23.25
mm
B.22.50
mm
C.21.75
mm
D.21.25
mm
10.若函数在上是单调函数,则的取值范围是(
)
A.
B.
C.
D.
11.某学校派出5名优秀教师去边远地区三所中学进行教学交流,每所中学至少派一名教师,则不同的分配方法有(
)
A.80种
B.90种
C.120种
D.150种
12.已知函数有两个零点,,且,则下列说法错误的是(
)
A.
B.
C.
D.有极小值点,且
二.填空题:本题共4小题,每小题5分,共20分,请将答案写在答题纸指定的位置上。
13.某气象台统计,该地区下雨的概率为,刮四级以上风的概率为,既刮四级以上的风又下雨的概率为,设为下雨,为刮四级以上的风,则______.
14.直线与曲线在第一象限内围成的封闭图形的面积为______.
15.对某种产品的6件不同的正品和4件不同次品一一进行测试,直到区分出所有次品为止。若所有次品恰好在第5次测试被全部发现,则这样的测试方法有______种。
16.下列命题中,正确命题的序号为______.
①已知随机变量服从二项分布,若,,则;
②将一组数据中的每个数据都加上同一个常数后,方差恒不变;
③某厂家声称自己的产品合格率为99%,市场质量管理人员抽取了这个厂家的2件产品进行检验,发现不都合格,由此可知厂家所声称的合格率不可信。
④某人在10次射击中,击中目标的次数为,,则当时概率最大.
三、解答题:本题共6小题,满分70分。解答应写出文字说明、证明过程或演算步骤。
17.(本题满分10分)
张先生家住小区,他在科技园区工作,从家开车到公司上班有,两条路线(如图),路线上有,,三个路口,各路口遇到红灯的均为;上有,两个路口,各路口遇到红灯的概率依次为,.
(1)若走路线,求最多遇到1次红灯的概率;
(2)若走路线,求他遇到红灯的次数的分布列和数学期望.
18.(本题满分12分)
已知某单位甲、乙、丙三个部门员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(2)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.用表示抽取的3人中睡眠不足的员工人数,求随机变量的分布列和数学期望;
19.(本题满分12分)
已知函数,.
(1)若,求曲线在点处的切线方程;
(2)若对于任意,都有成立,求实数的取值范围.
20.(本题满分12分)耐盐碱水稻俗称“海水稻”,是一种可以长在滩涂和盐碱地的水稻,海水稻的灌溉是将海水稀释后进行灌溉,某试验基地为了研究海水浓度对亩产量(吨)的影响,通过在试验田的种植实验,测得了某种海水稻的亩产量与海水浓度的数据如表,绘制散点图发现,可用线性回归模型拟合亩产量与海水浓度之间的相关关系,用最小二乘法计算得与之间的线性回归方程为.
(1)求,并估计当浇灌海水浓度为8时该品种的亩产量;
(2)(i)完成下列残差表:
海水浓度
3
4
5
6
7
亩产量(吨)
0.62
0.58
0.49
0.4
0.31
残差
(ii)统计学中常用相关指数来刻画回归效果,越大,模型拟合效果越好,如假设,就说明预报变量的差异有80%是由解释变量引起的,请计算相关指数(精确到0.01),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的?
附:残差公式,相关指数
21.(本题满分12分)为了解某品种一批树苗生长情况,在该批树苗中随机抽取了容量为120的样本,测量树苗高度(单位:cm),经统计,其高度均在区间内,将其按,,,,,分成6组,制成如图所示的频率分布直方图.其中高度为27cm及以上的树苗为优质树苗.
(1)求图中的值
(2)已知抽取这120棵树苗来自于A,B两个试验区,部分数据如下列联表:
A试验区
B试验区
合计
优质树苗
20
非优质树苗
60
合计
将列联表补充完整,并判断是否有99.9%的把握认为优质树苗与A,B两个试验区有关系,并说明理由;
(3)用样本估计总体,
若从这批树苗中随机抽取4棵,其中优质树苗的棵数为,求的数学期望.
下面的临界值表仅供参考:
0.15
0.10
0.05
0.25
0.01
0.005
0.001
2.702
2.706
3.841
5.024
6.635
7.879
10.828
参考公式:,其中.
22.(本题满分12分)
已知函数,
.
(1)若,求的取值范围;
(2)当时,证明:.
期末数学理答案
1-12
CBABA
DCABB
DC
13.;14.4;15.576;16.②③④.
17.(1)设走路线最多遇到1次红灯为事件,则.
(2)依题意,的可能取值为0,1,2.
则;;
,
随机变量的分布列为:
0
1
2
.
18.(1)由己知,甲、乙、丙三个部门的员工人数之比为3:2:2,由于采用分层抽样的方法从中抽取7人。因此应从甲、乙、两三个部门的员工中分别抽取3人,2人,2人.
(2)随机变量的所有可能取值为0,1,2,3.
.
所以。随机变量的分布列为
0
1
2
3
随机变量的数学期望.
19.(1),,
,则.
所以在点处的切线方程为,即.
(2)因为对于任意,都有成立,所以,
即问题转化为对于恒成立,即
对于恒成立,令,则,
令,,则.所以在区间上单调递增,
故,进而,所以在区间上单调递增,
函数,
要使对于恒成立,只要,所以,即实数的取值范围是.
20.(1)经计算,,,
由可得,,
当时,,所以当海水浓度为8时,该品种的亩产量为0.24吨.
(2)(i)由(1)知,从而有
浓度(千分之)
3
4
5
6
7
亩产量(吨)
0.62
0.58
0.49
0.4
0.31
残差
-0.02
0.02
0.01
0
-0.01
(ii),所以亩产量的变化有98%是由海水引起的.
21.(1)根据直方图数据,有,解得.
(2)根据直方图可知,样本中优质树苗有,列联表如下:
A试验区
B试验区
合计
优质树苗
10
20
30
非优质树苗
60
30
90
合计
70
50
120
可得.
所以,没有99.9%的把握认为优质树苗与A,B两个试验区有关系.
(3)由己知,这批树苗为优质树苗的概率为,且服从二项分布,故数学期望.
22.(1),
当时,.所以函数在上单调递增,所以,满足题意.
当时,,函数在上单调递减,,不符合题意.
当时,令,在存在,使得成立,
所以时,,函数在上单调递减,则,不符合题意.
综上,的取值范围为.
(2)当时,,
要证,即证,即,
设,则
.
由(1)知,又,
所以,所以在上单调递增,故,
所以,,.
