科学命题同步练习之23.1图形的旋转(含解析)
文档属性
| 名称 | 科学命题同步练习之23.1图形的旋转(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
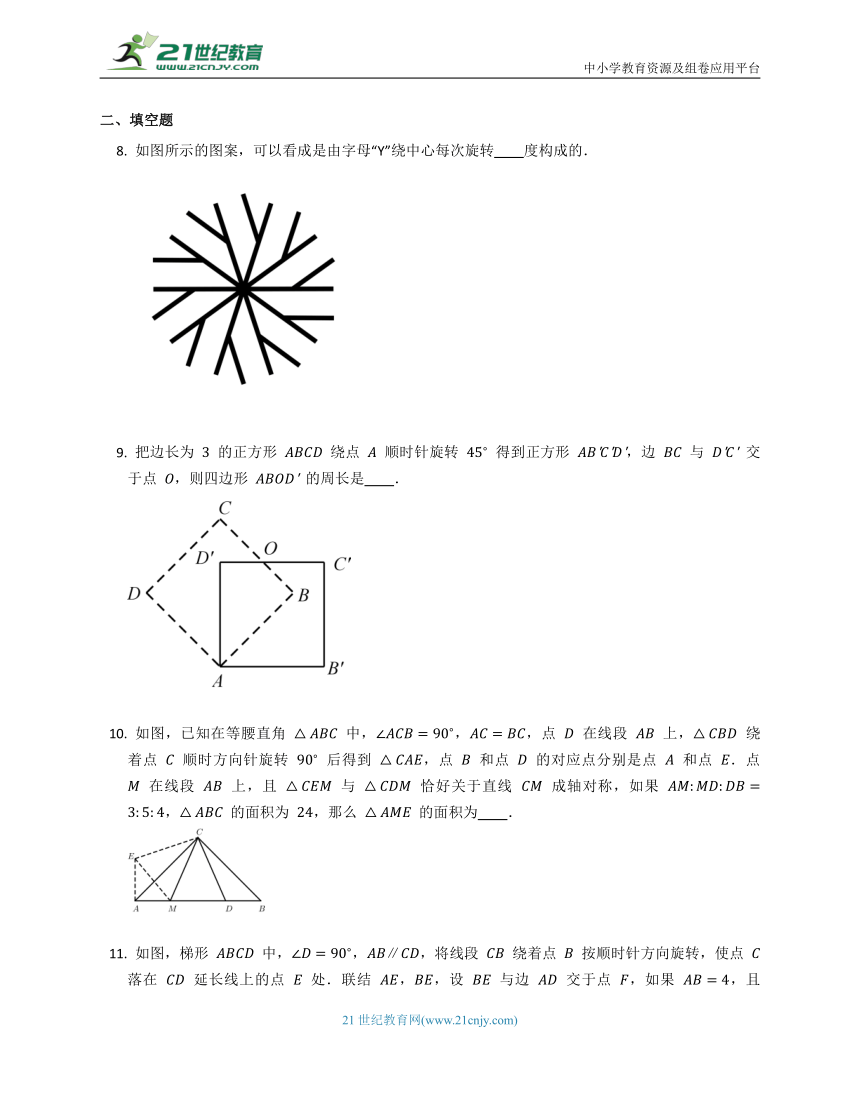
科学命题同步练习之23.1图形的旋转
一、选择题
如图,将
绕点
顺时针旋转
得到
,点
的对应点
恰好落在
的延长线上,
与
交于点
,连接
.下列结论不一定正确的是
A.
B.
C.
D.
如图,在长方形
中,
是对角线,将
绕点
顺的针旋转
到
位置,
是
的中点,若
,,则线段
的长为
A.
B.
C.
D.
如图,将
绕点
按逆时针方向旋转
后得到
,若
,则
的度数是
A.
B.
C.
D.
如图,
中,.将
绕点
顺时针旋转
得到
,边
与边
交于点
(
不在
上),则
的度数为
A.
B.
C.
D.
如图,边长为
的等边
中,
是高
所在直线上的一个动点,连接
,将线段
绕点
逆时针旋转
得到
,连接
.则在点
运动过程中,线段
长度的最小值是
A.
B.
C.
D.
如图,把
绕点
逆时针旋转
,得到
,点
恰好落在边
上的点
处,连接
,则
的度数为
A.
B.
C.
D.
如图,边长为
的正五边形
,顶点
,
在半径为
的圆上,其他各点在圆内,将正五边形
绕点
逆时针旋转,当点
第一次落在圆上时,则点
转过的度数为
A.
B.
C.
D.
二、填空题
如图所示的图案,可以看成是由字母“Y”绕中心每次旋转
度构成的.
把边长为
的正方形
绕点
顺时针旋转
得到正方形
,边
与
交于点
,则四边形
的周长是
.
如图,已知在等腰直角
中,,,点
在线段
上,
绕着点
顺时方向针旋转
后得到
,点
和点
的对应点分别是点
和点
.点
在线段
上,且
与
恰好关于直线
成轴对称,如果
,
的面积为
,那么
的面积为
.
如图,梯形
中,,,将线段
绕着点
按顺时针方向旋转,使点
落在
延长线上的点
处.联结
,,设
与边
交于点
,如果
,且
,那么梯形
的中位线等于
.
在正方形
中,点
在边
上,点
在线段
上,且
,,,则
度,四边形
的面积
.
三、解答题
将一副三角板中的两块直角三角尺的直角顶点
按如图方式叠放在一起.
(1)
如图
,若
,则
;若
,则
;
(2)
如图
,若
,则
;
(3)
猜想
与
的大小关系,并结合图
说明理由.
(4)
三角尺
不动,将三角尺
的
边与
边重合,然后绕点
按顺时针或逆时针方向任意转动一个角度,当
等于多少度时,这两块三角尺各有一条边互相垂直,直接写出
角度所有可能的值,不用说明理由.
如图①,在平行四边形
中,,,点
为对角线
上一动点,连接
,将
绕点
逆时针旋转
得到
,连接
.
(1)
求证
;
(2)
如图②,若
点恰好落在
,求
的长;
(3)
如图③,当点
落在
的外部,构成四边形
时,求四边形
的面积.
已知:在
中,,.
(1)
如图
,将线段
绕点
逆时针旋转
得到
,连接
,,
的平分线交
于点
,连接
.
①求证:;
②用等式表示线段
,,
之间的数量关系(直接写出结果);
(2)
在图
中,若将线段
绕点
顺时针旋转
得到
,连接
,,
的平分线交
的延长线于点
,连接
.请补全图形,并用等式表示线段
,,
之间的数量关系,并证明.
如图1,在平面直角坐标系中,
是直角三角形,,,,,抛物线
经过
、
两点,顶点为
.
(1)
求
、
的值;
(2)
若点
是
斜边
上一动点(点
、
除外),连接
,,当
的值最小时,求
的面积;
(3)
如图2,连接
,将
绕点
旋转
,直线
与直线
交于点
,直线
与直线
交于点
,当
是等腰三角形时,直接写出所有点
的坐标.
答案
一、选择题
1.
【答案】C
【解析】由旋转知
,,,
,
是等边三角形,,
,,
,
,
,
则A,B,D均正确.
【知识点】旋转及其性质
2.
【答案】D
【知识点】旋转及其性质
3.
【答案】B
【解析】
将
绕点
按逆时针方向旋转
后得到
,
,,
.
【知识点】旋转及其性质
4.
【答案】D
【解析】
是由
绕点
顺时针旋转得到,,
,
绕点
顺时针旋转
,
,
是
的外角,
.
【知识点】旋转及其性质、三角形的外角及外角性质
5.
【答案】A
【解析】如图,取
的中点
,连接
.
旋转角为
,
.
又
,
.
是等边
的对称轴,
.
.
又
旋转到
,
.
在
和
中,
.
.
根据垂线段最短,
时,
最短,即
最短.
此时
,,
.
.
【知识点】旋转及其性质、等边三角形的性质
6.
【答案】D
【解析】
把
绕点
逆时针旋转
,
得到
,点
恰好落在边
上,
,,
.
的度数为
.
【知识点】旋转及其性质
7.
【答案】A
【知识点】旋转及其性质、正多边形的有关计算
二、填空题
8.
【答案】
【解析】根据图形可得:这是一个由字母“Y”绕着中心连续旋转
次,每次旋转
度角形成的图案.
【知识点】旋转及其性质
9.
【答案】
【解析】连接
,,如图,
边长为
的正方形
绕点
顺时针旋转
得到正方形
,
,,
点
,,
共线,点
,,
共线,
和
都是等腰直角三角形,
,,
,
四边形
的周长
.
【知识点】旋转及其性质、正方形的性质
10.
【答案】
【解析】由题意得:根据勾股定理和面积可求出
,
进而求出
,
又
,
得
,
又由旋转得
,
是直角三角形,
.
【知识点】勾股定理、旋转及其性质
11.
【答案】
【知识点】梯形的中位线、旋转及其性质、相似三角形的性质与判定
12.
【答案】
;
【解析】如图,
四边形
是正方形,
,,
将
绕点
顺时针旋转
到
,连接
,过
作
于
,
由旋转得:,,,
,,
,,
,
,
,
,
是等腰直角三角形,
,
,
,
由勾股定理得:,
【知识点】旋转及其性质、正方形的性质、勾股逆定理
三、解答题
13.
【答案】
(1)
;
(2)
(3)
与
互补.
.
,
,
即
与
互补.
(4)
角度所有可能的值为:,,,.
【解析】
(1)
若
,
.
,
若
,
则
.
(2)
如图
,若
,
则
.
(4)
时,,
时,,
时,,
时,,
即
角度所有可能的值为:,,,.
【知识点】角的计算、旋转及其性质、余角,补角
14.
【答案】
(1)
绕点
逆时针旋转
得到
,
,,
,
,
,
,
,
.
(2)
过
作
于
.
四边形
是平行四边形
,,
,
,
,,
,
,
,,,
,(点
与
重合),
,
,,,
,
,
,
,
.
(3)
如图,将
绕点
逆时针旋转
得到
.
,,,
,
,
,
点
,点
,点
三点共线,
,
四边形
是矩形,
又
,
四边形
为正方形,
.
【知识点】平行四边形及其性质、旋转及其性质、正方形的判定、勾股定理
15.
【答案】
(1)
①
将线段
绕点
逆时针旋转
得到
,
,.
且
.
.
,,
平分
,
,.
又
,
.
.
.
.
,
.
②
.
(2)
补全图形如图.
,理由如下:
如图
,以
为顶点,
为一边作
,
交
延长线于点
.
,,
平分
,
,.
将线段
绕点
逆时针旋转
得到
,
,.
,.
,.
.
.
,
又
,
.
是等边三角形.
.
,,,
.
.
,,,
.
.
.
,
.
【解析】
(1)
②理由如下:
过点
作
于点
,
,
.
,,
.
,,
.
【知识点】等边三角形的判定、边角边、30度所对的直角边等于斜边的一半、旋转及其性质
16.
【答案】
(1)
,,,
,,.
抛物线
经过
、
两点,
解得
(2)
由(1)易得:,直线
的解析式为
,
点
关于直线
的对称点为
.
直线
的解析式为
,
直线
与直线
的交点即为
,
过点
做
交直线
于
,可得
,
所以
.
(3)
绕点
旋转至
,
,
是等腰三角形,.
把
是等腰三角形转化为
是等腰三角形即在直线
上找一点
使
是等腰三角形,
易得
,,,.
【知识点】等腰三角形的性质、旋转及其性质、二次函数的解析式、一次函数的解析式
21世纪教育网(www.21cnjy.com)
科学命题同步练习之23.1图形的旋转
一、选择题
如图,将
绕点
顺时针旋转
得到
,点
的对应点
恰好落在
的延长线上,
与
交于点
,连接
.下列结论不一定正确的是
A.
B.
C.
D.
如图,在长方形
中,
是对角线,将
绕点
顺的针旋转
到
位置,
是
的中点,若
,,则线段
的长为
A.
B.
C.
D.
如图,将
绕点
按逆时针方向旋转
后得到
,若
,则
的度数是
A.
B.
C.
D.
如图,
中,.将
绕点
顺时针旋转
得到
,边
与边
交于点
(
不在
上),则
的度数为
A.
B.
C.
D.
如图,边长为
的等边
中,
是高
所在直线上的一个动点,连接
,将线段
绕点
逆时针旋转
得到
,连接
.则在点
运动过程中,线段
长度的最小值是
A.
B.
C.
D.
如图,把
绕点
逆时针旋转
,得到
,点
恰好落在边
上的点
处,连接
,则
的度数为
A.
B.
C.
D.
如图,边长为
的正五边形
,顶点
,
在半径为
的圆上,其他各点在圆内,将正五边形
绕点
逆时针旋转,当点
第一次落在圆上时,则点
转过的度数为
A.
B.
C.
D.
二、填空题
如图所示的图案,可以看成是由字母“Y”绕中心每次旋转
度构成的.
把边长为
的正方形
绕点
顺时针旋转
得到正方形
,边
与
交于点
,则四边形
的周长是
.
如图,已知在等腰直角
中,,,点
在线段
上,
绕着点
顺时方向针旋转
后得到
,点
和点
的对应点分别是点
和点
.点
在线段
上,且
与
恰好关于直线
成轴对称,如果
,
的面积为
,那么
的面积为
.
如图,梯形
中,,,将线段
绕着点
按顺时针方向旋转,使点
落在
延长线上的点
处.联结
,,设
与边
交于点
,如果
,且
,那么梯形
的中位线等于
.
在正方形
中,点
在边
上,点
在线段
上,且
,,,则
度,四边形
的面积
.
三、解答题
将一副三角板中的两块直角三角尺的直角顶点
按如图方式叠放在一起.
(1)
如图
,若
,则
;若
,则
;
(2)
如图
,若
,则
;
(3)
猜想
与
的大小关系,并结合图
说明理由.
(4)
三角尺
不动,将三角尺
的
边与
边重合,然后绕点
按顺时针或逆时针方向任意转动一个角度,当
等于多少度时,这两块三角尺各有一条边互相垂直,直接写出
角度所有可能的值,不用说明理由.
如图①,在平行四边形
中,,,点
为对角线
上一动点,连接
,将
绕点
逆时针旋转
得到
,连接
.
(1)
求证
;
(2)
如图②,若
点恰好落在
,求
的长;
(3)
如图③,当点
落在
的外部,构成四边形
时,求四边形
的面积.
已知:在
中,,.
(1)
如图
,将线段
绕点
逆时针旋转
得到
,连接
,,
的平分线交
于点
,连接
.
①求证:;
②用等式表示线段
,,
之间的数量关系(直接写出结果);
(2)
在图
中,若将线段
绕点
顺时针旋转
得到
,连接
,,
的平分线交
的延长线于点
,连接
.请补全图形,并用等式表示线段
,,
之间的数量关系,并证明.
如图1,在平面直角坐标系中,
是直角三角形,,,,,抛物线
经过
、
两点,顶点为
.
(1)
求
、
的值;
(2)
若点
是
斜边
上一动点(点
、
除外),连接
,,当
的值最小时,求
的面积;
(3)
如图2,连接
,将
绕点
旋转
,直线
与直线
交于点
,直线
与直线
交于点
,当
是等腰三角形时,直接写出所有点
的坐标.
答案
一、选择题
1.
【答案】C
【解析】由旋转知
,,,
,
是等边三角形,,
,,
,
,
,
则A,B,D均正确.
【知识点】旋转及其性质
2.
【答案】D
【知识点】旋转及其性质
3.
【答案】B
【解析】
将
绕点
按逆时针方向旋转
后得到
,
,,
.
【知识点】旋转及其性质
4.
【答案】D
【解析】
是由
绕点
顺时针旋转得到,,
,
绕点
顺时针旋转
,
,
是
的外角,
.
【知识点】旋转及其性质、三角形的外角及外角性质
5.
【答案】A
【解析】如图,取
的中点
,连接
.
旋转角为
,
.
又
,
.
是等边
的对称轴,
.
.
又
旋转到
,
.
在
和
中,
.
.
根据垂线段最短,
时,
最短,即
最短.
此时
,,
.
.
【知识点】旋转及其性质、等边三角形的性质
6.
【答案】D
【解析】
把
绕点
逆时针旋转
,
得到
,点
恰好落在边
上,
,,
.
的度数为
.
【知识点】旋转及其性质
7.
【答案】A
【知识点】旋转及其性质、正多边形的有关计算
二、填空题
8.
【答案】
【解析】根据图形可得:这是一个由字母“Y”绕着中心连续旋转
次,每次旋转
度角形成的图案.
【知识点】旋转及其性质
9.
【答案】
【解析】连接
,,如图,
边长为
的正方形
绕点
顺时针旋转
得到正方形
,
,,
点
,,
共线,点
,,
共线,
和
都是等腰直角三角形,
,,
,
四边形
的周长
.
【知识点】旋转及其性质、正方形的性质
10.
【答案】
【解析】由题意得:根据勾股定理和面积可求出
,
进而求出
,
又
,
得
,
又由旋转得
,
是直角三角形,
.
【知识点】勾股定理、旋转及其性质
11.
【答案】
【知识点】梯形的中位线、旋转及其性质、相似三角形的性质与判定
12.
【答案】
;
【解析】如图,
四边形
是正方形,
,,
将
绕点
顺时针旋转
到
,连接
,过
作
于
,
由旋转得:,,,
,,
,,
,
,
,
,
是等腰直角三角形,
,
,
,
由勾股定理得:,
【知识点】旋转及其性质、正方形的性质、勾股逆定理
三、解答题
13.
【答案】
(1)
;
(2)
(3)
与
互补.
.
,
,
即
与
互补.
(4)
角度所有可能的值为:,,,.
【解析】
(1)
若
,
.
,
若
,
则
.
(2)
如图
,若
,
则
.
(4)
时,,
时,,
时,,
时,,
即
角度所有可能的值为:,,,.
【知识点】角的计算、旋转及其性质、余角,补角
14.
【答案】
(1)
绕点
逆时针旋转
得到
,
,,
,
,
,
,
,
.
(2)
过
作
于
.
四边形
是平行四边形
,,
,
,
,,
,
,
,,,
,(点
与
重合),
,
,,,
,
,
,
,
.
(3)
如图,将
绕点
逆时针旋转
得到
.
,,,
,
,
,
点
,点
,点
三点共线,
,
四边形
是矩形,
又
,
四边形
为正方形,
.
【知识点】平行四边形及其性质、旋转及其性质、正方形的判定、勾股定理
15.
【答案】
(1)
①
将线段
绕点
逆时针旋转
得到
,
,.
且
.
.
,,
平分
,
,.
又
,
.
.
.
.
,
.
②
.
(2)
补全图形如图.
,理由如下:
如图
,以
为顶点,
为一边作
,
交
延长线于点
.
,,
平分
,
,.
将线段
绕点
逆时针旋转
得到
,
,.
,.
,.
.
.
,
又
,
.
是等边三角形.
.
,,,
.
.
,,,
.
.
.
,
.
【解析】
(1)
②理由如下:
过点
作
于点
,
,
.
,,
.
,,
.
【知识点】等边三角形的判定、边角边、30度所对的直角边等于斜边的一半、旋转及其性质
16.
【答案】
(1)
,,,
,,.
抛物线
经过
、
两点,
解得
(2)
由(1)易得:,直线
的解析式为
,
点
关于直线
的对称点为
.
直线
的解析式为
,
直线
与直线
的交点即为
,
过点
做
交直线
于
,可得
,
所以
.
(3)
绕点
旋转至
,
,
是等腰三角形,.
把
是等腰三角形转化为
是等腰三角形即在直线
上找一点
使
是等腰三角形,
易得
,,,.
【知识点】等腰三角形的性质、旋转及其性质、二次函数的解析式、一次函数的解析式
21世纪教育网(www.21cnjy.com)
同课章节目录
