小数人教版 -六下-4-圆柱 课件(15张PPT)
文档属性
| 名称 | 小数人教版 -六下-4-圆柱 课件(15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-02 08:57:46 | ||
图片预览




文档简介
(共15张PPT)
圆 柱
圆柱
你还见过哪些圆柱形的物体?
上面这些物体的形状都是圆柱体。
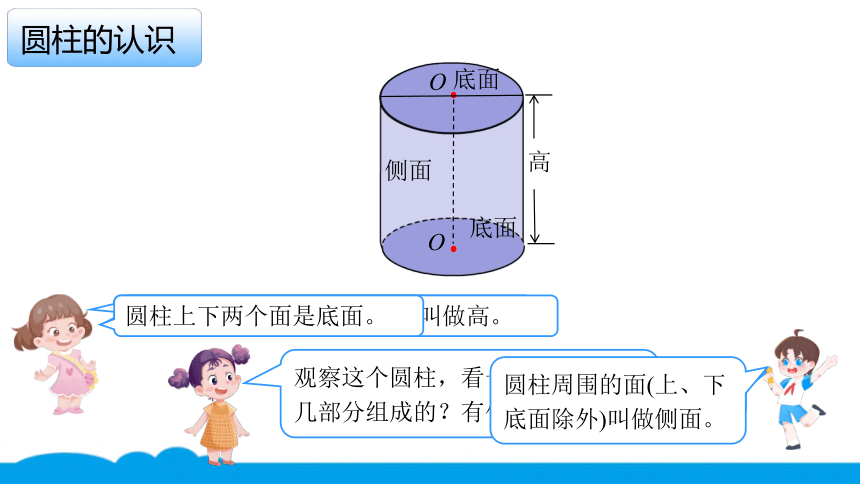
圆柱的认识
侧面
底面
底面
O
O
高
圆柱的侧面是曲面。
圆柱的底面都是圆,并且大小一样。
圆柱的两个底面之间的距离叫做高。
观察这个圆柱,看一看它是由哪几部分组成的?有什么特征?
圆柱周围的面(上、下底面除外)叫做侧面。
圆柱上下两个面是底面。
圆柱的认识
如果把一张长方形的硬纸贴在木棒上,快速转动木棒,想一想,转出来的是什么形状?
转动起来像一个圆柱。
圆柱的认识
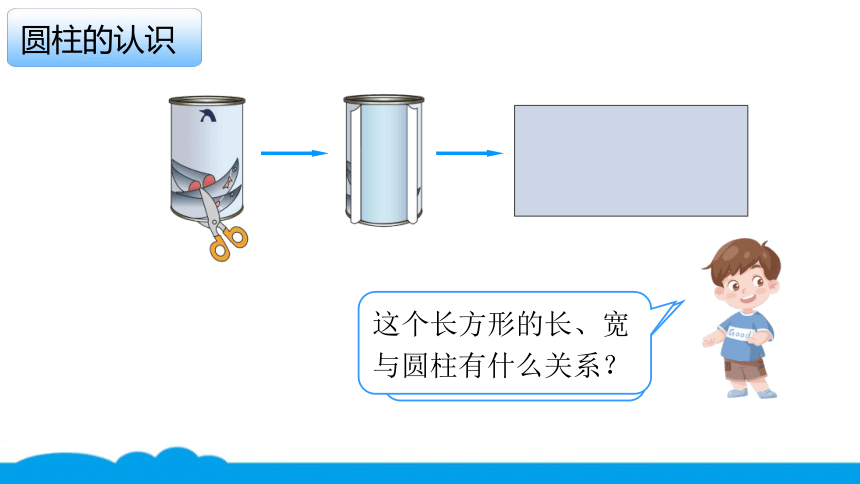
圆柱侧面展开后得到一个长方形。
这个长方形的长、宽与圆柱有什么关系?
圆柱的认识
底面
底面
底面的周长
底面
底面
高
底面的周长
高
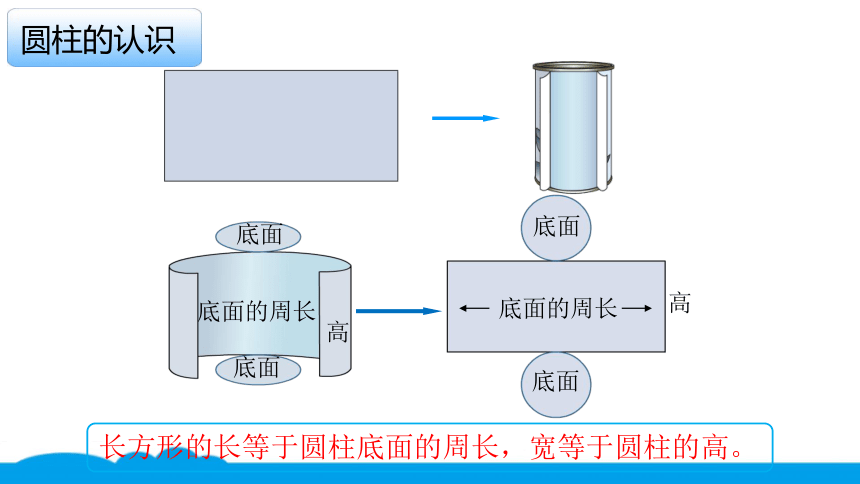
长方形的长等于圆柱底面的周长,宽等于圆柱的高。
圆柱的表面积
圆柱的表面积指的是什么?
S =Ch
侧
=πdh
=2πrh
圆柱的侧面积=长方形的面积
=长 × 宽
=圆柱的底面周长×高
高
底面的周长
侧面
底面的周长
高
圆柱的侧面积
你发现了什么?
底面
底面
底面的周长
底面
底面
高
底面的周长
高
圆柱的表面积=圆柱的侧面积+两个底面的面积
S =S +2S
表
侧
圆
圆柱的表面积
=2πrh+2πr
圆柱的表面积
一顶圆柱形厨师帽,高30cm,帽顶直径20cm,做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数)
帽子的侧面积:3.14×20×30=1884(cm2 )
帽顶的面积:3.14×(20÷2) =314(cm2 )
需要用的面料:1884+314=2198≈2200(cm2 )
答:做这样一顶帽子至少要用2200cm2的面料。
想一想:求多少面料就是求什么?
“没有底”的帽子如果展开,它由哪几部分组成?
实际使用的面料要比计算的结果多一些,所以这类问题往往用“进一法”取近似数。
“没有底”的帽子的展开图,它是由一个底面和一个侧面组成。
圆柱的体积
分成的扇形越多,拼成的立体图形就越接近于长方体。
把圆柱的底面分成许多相同的扇形。
把圆柱切开,再像这样拼起来,得到一个近似的长方体。
圆柱的体积
长方体的体积与圆柱的体积相等。
长方体的底面积等于圆柱的底面积。
把拼成的长方体与原来的圆柱比较,你能发现什么?
长方体的高等于圆柱的高。
圆柱的体积= 底面积 × 高
长方体的体积= 底面积 × 高
V
V
圆柱的体积利用半径的计算公式是:
=
S
h
πr h
圆柱的体积
=
8cm
10cm
=3.14×4
=3.14×16
=50.24 (cm2 )
3.14×(8÷2)
杯子的底面积=πr
杯子的容积=Sh
下图的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的)
圆柱的体积
答:因为502.4大于498,所以杯子能装下这袋牛奶。
50.24×10
=502.4 (cm3 )
=502.4 (mL )
谢谢观看!
圆 柱
圆柱
你还见过哪些圆柱形的物体?
上面这些物体的形状都是圆柱体。
圆柱的认识
侧面
底面
底面
O
O
高
圆柱的侧面是曲面。
圆柱的底面都是圆,并且大小一样。
圆柱的两个底面之间的距离叫做高。
观察这个圆柱,看一看它是由哪几部分组成的?有什么特征?
圆柱周围的面(上、下底面除外)叫做侧面。
圆柱上下两个面是底面。
圆柱的认识
如果把一张长方形的硬纸贴在木棒上,快速转动木棒,想一想,转出来的是什么形状?
转动起来像一个圆柱。
圆柱的认识
圆柱侧面展开后得到一个长方形。
这个长方形的长、宽与圆柱有什么关系?
圆柱的认识
底面
底面
底面的周长
底面
底面
高
底面的周长
高
长方形的长等于圆柱底面的周长,宽等于圆柱的高。
圆柱的表面积
圆柱的表面积指的是什么?
S =Ch
侧
=πdh
=2πrh
圆柱的侧面积=长方形的面积
=长 × 宽
=圆柱的底面周长×高
高
底面的周长
侧面
底面的周长
高
圆柱的侧面积
你发现了什么?
底面
底面
底面的周长
底面
底面
高
底面的周长
高
圆柱的表面积=圆柱的侧面积+两个底面的面积
S =S +2S
表
侧
圆
圆柱的表面积
=2πrh+2πr
圆柱的表面积
一顶圆柱形厨师帽,高30cm,帽顶直径20cm,做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数)
帽子的侧面积:3.14×20×30=1884(cm2 )
帽顶的面积:3.14×(20÷2) =314(cm2 )
需要用的面料:1884+314=2198≈2200(cm2 )
答:做这样一顶帽子至少要用2200cm2的面料。
想一想:求多少面料就是求什么?
“没有底”的帽子如果展开,它由哪几部分组成?
实际使用的面料要比计算的结果多一些,所以这类问题往往用“进一法”取近似数。
“没有底”的帽子的展开图,它是由一个底面和一个侧面组成。
圆柱的体积
分成的扇形越多,拼成的立体图形就越接近于长方体。
把圆柱的底面分成许多相同的扇形。
把圆柱切开,再像这样拼起来,得到一个近似的长方体。
圆柱的体积
长方体的体积与圆柱的体积相等。
长方体的底面积等于圆柱的底面积。
把拼成的长方体与原来的圆柱比较,你能发现什么?
长方体的高等于圆柱的高。
圆柱的体积= 底面积 × 高
长方体的体积= 底面积 × 高
V
V
圆柱的体积利用半径的计算公式是:
=
S
h
πr h
圆柱的体积
=
8cm
10cm
=3.14×4
=3.14×16
=50.24 (cm2 )
3.14×(8÷2)
杯子的底面积=πr
杯子的容积=Sh
下图的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的)
圆柱的体积
答:因为502.4大于498,所以杯子能装下这袋牛奶。
50.24×10
=502.4 (cm3 )
=502.4 (mL )
谢谢观看!
