2020-2021学年人教版数学八年级上册:11.3.2多边形的内角和 课件(25张PPT)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册:11.3.2多边形的内角和 课件(25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 06:58:26 | ||
图片预览



文档简介
课前复习与思考
180°
其他任意四边形的内角和是 ___
猜一猜:
360°
你有什么方法得到四边形的内角和吗?
2、从n边形的一个顶点出发可以引 条对角线,它们将多边形分成 个三角形。
(n-3)
(n-2)
1、三角形的内角和是 ,长方形、正方形的内角和是 。
360°
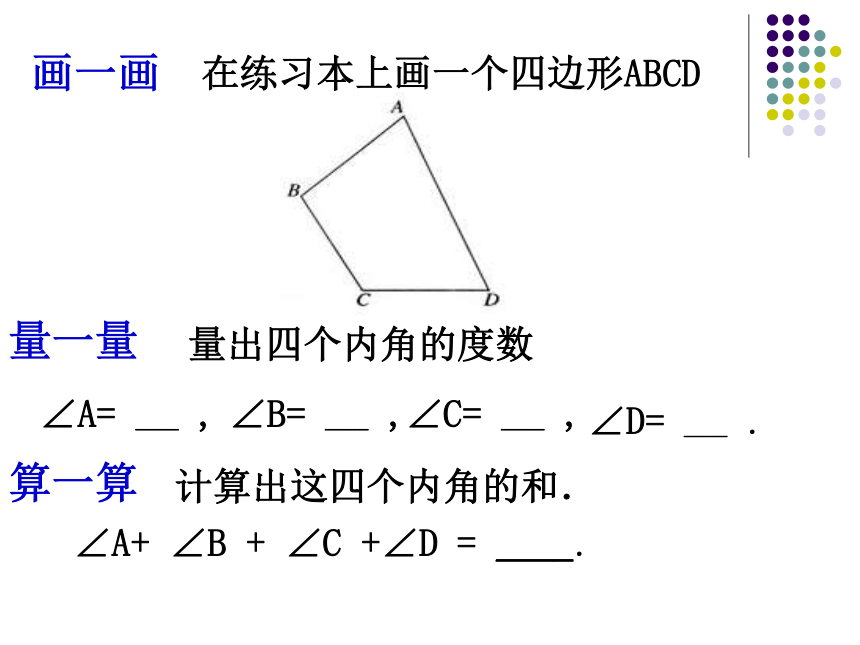
画一画
在练习本上画一个四边形ABCD
∠A= ____ ,
∠B= ____ ,
∠C= ____ ,
∠D= ____ .
∠A+ ∠B + ∠C +∠D = ____.
量一量
量出四个内角的度数
算一算
计算出这四个内角的和.
A
B
c
D
E
A
B
c
D
E
A
B
c
D
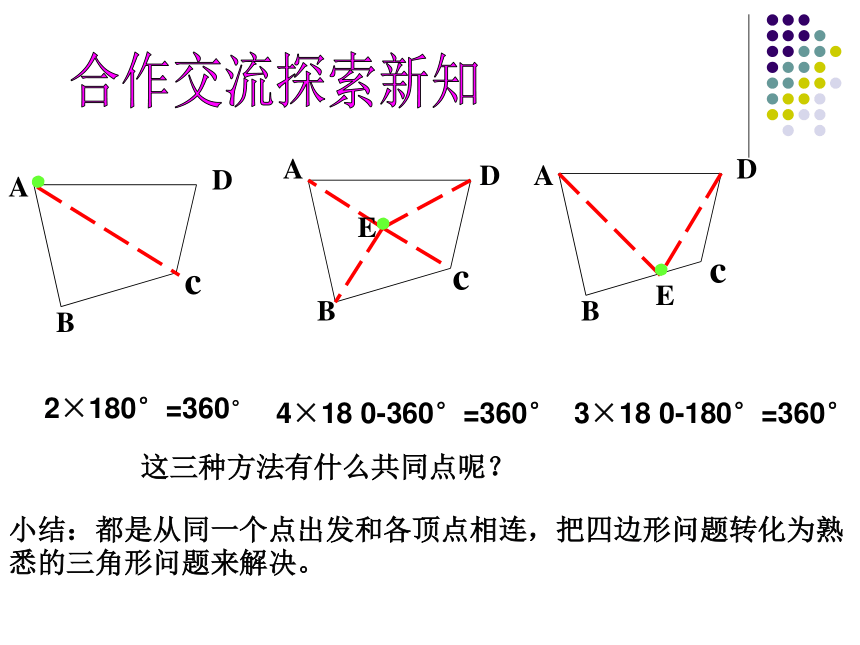
小结:都是从同一个点出发和各顶点相连,把四边形问题转化为熟悉的三角形问题来解决。
这三种方法有什么共同点呢?
2×180°=360°
3×18 0-180°=360°
4×18 0-360°=360°
.
.
.
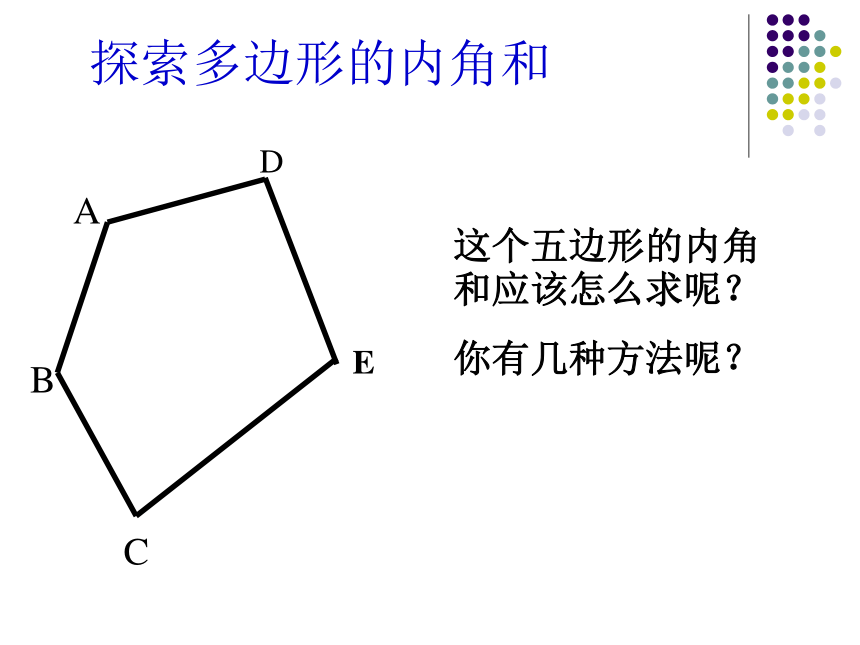
探索多边形的内角和
这个五边形的内角和应该怎么求呢?
你有几种方法呢?
A
C
D
E
B
A
C
E
D
B
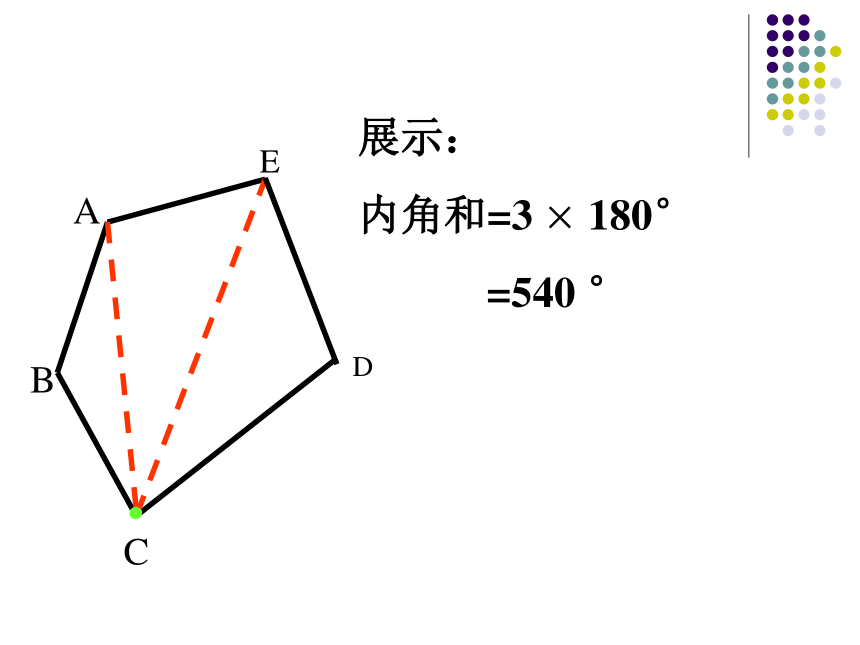
展示:
内角和=3 × 180°
=540 °
.
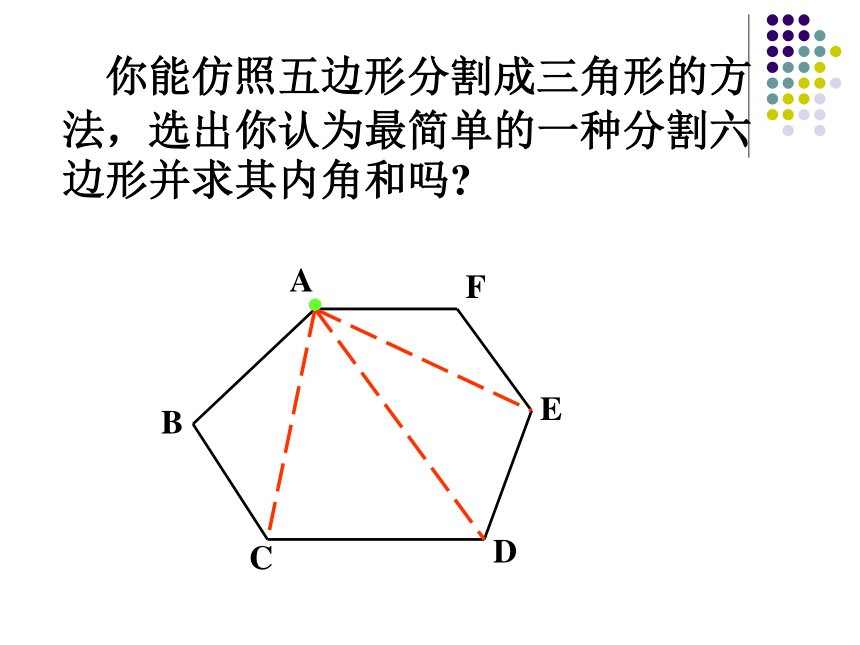
你能仿照五边形分割成三角形的方法,选出你认为最简单的一种分割六边形并求其内角和吗?
A
B
C
D
E
F
.
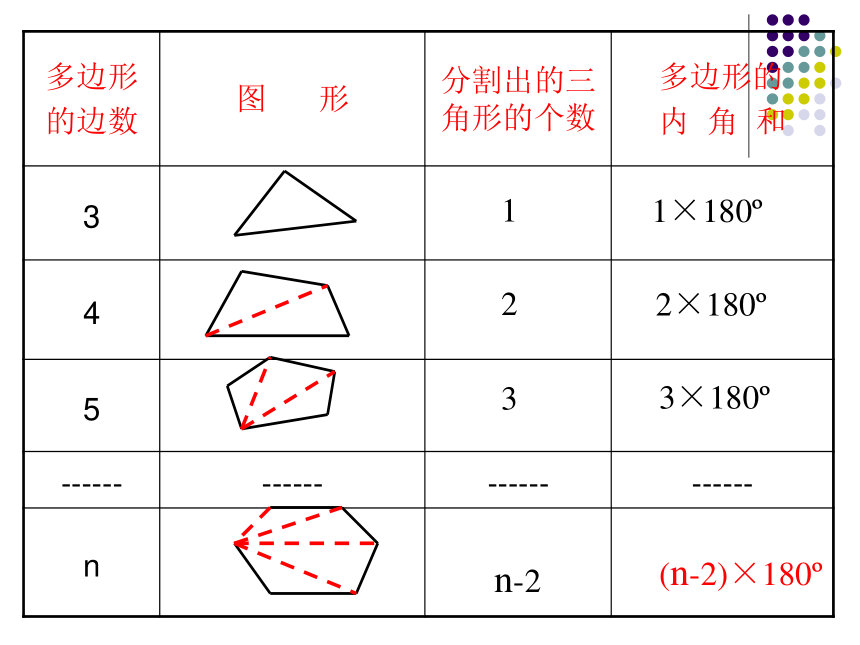
多边形
的边数
图 形
分割出的三角形的个数
多边形的
内 角 和
3
4
5
------
------
------
------
n
n-2
1
2
3
1×180?
2×180?
3×180?
(n-2)×180?
综上所述,设多边形的边数为n,
则 n边形的内角和等于
(n-2)×180?
?
知道了多边形的内角和,它可以解决哪些问题呢?
?
1、已知边数,求内角和
2、已知内角和求边数
1.十二边形的内角和等于______度.
2.已知多边形的每个内角都是135度,则这个
多边形是_______.
3.一个多边形当边数增加1时,它的内角和
增加 度。
4.过多边形的一个顶点可以引7条对角线,那么这个多边形的内角和是 。
1800
八边形
180
1440°
1、一个多边形的内角和等于900°,它是几边形?
2、求下列图形中 x的值
如果一个四边形的一组对角互补,
那么另一组对角有什么关系?
解:
如图,四边形ABCD中,
∠A+ ∠C =180°
∠A+∠B+∠C+∠D=(4-2) ×180 °
= 360 °
因为
∠B+∠D
= 360°-(∠A+∠C)
= 360°- 180°
=180°
这就是说:如果四边形一组对角互补,那么另一组对角也互补.
所以
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
用形状、大小完全相同的任意四边形可拼成一块无空隙的地板,你知道这是为什么吗?
1、n边形的内角和等于(n-2)×180°,公式的应用;
2、转化的方法.
这节课我们学到了什么?
A
C
D
E
B
.
2、你能用多边形的内角和公式推导多边形的外角和吗?
1、你能用左图推导多边形的内角和公式吗?
如图,在正五边形ABCDE中,连接BE,求∠BED的度数.
解:由题意得
AB=AE,所以∠AEB= (180°–∠A)=36°,
所以∠BED=∠AED–∠AEB=108°–36°=72°.
巩固练习
1.已知正多边形的一个外角等于40°,那么这个正多边形的边数为( )
A.6 B.7 C.8 D.9
解析:正多边形的一个外角等于40°,且外角和为360°,则这个正多边形的边数是:360°÷40°=9.
D
连接中考
2.若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是_____.
解析:设多边形的边数为n,根据题意,得
(n–2)?180=3×360,
解得 n=8.
则这个多边形的边数是8.
8
连接中考
1.判断.
(1)当多边形边数增加时,它的内角和也随着增加.( )
(2)当多边形边数增加时,它的外角和也随着增加.( )
(3)三角形的外角和与八边形的外角和相等. ( )
2.一个多边形的每一个外角都是36°,则这个多边形的边数是 .
基础巩固题
10
课堂检测
3. 如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是________米.
150
课堂检测
4. 一个多边形从一个顶点可引对角线3条,这个多边形
内角和等于( )
A. 360° B. 540 °
C. 720 ° D. 900 °
B
课堂检测
一个多边形的内角和为1800°,截去一个角后,求得到的多边形的内角和.
能力提升题
课堂检测
如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
解:如图,
∵∠3+∠4=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7
=∠1+∠2+∠8+∠9+∠5+∠6+∠7
=五边形的内角和
=540°.
8
9
拓广探索题
课堂检测
多边形的内角和
内角和计算公式
(n–2) × 180 °(n ≥3的整数)① 边数增加1,内角和增加180°;②内角和是180°的整倍数.
外角和
多边形的外角和等于360°
特别注意:与边数无关.
正多
边形
内角= ,外角=
课堂小结
180°
其他任意四边形的内角和是 ___
猜一猜:
360°
你有什么方法得到四边形的内角和吗?
2、从n边形的一个顶点出发可以引 条对角线,它们将多边形分成 个三角形。
(n-3)
(n-2)
1、三角形的内角和是 ,长方形、正方形的内角和是 。
360°
画一画
在练习本上画一个四边形ABCD
∠A= ____ ,
∠B= ____ ,
∠C= ____ ,
∠D= ____ .
∠A+ ∠B + ∠C +∠D = ____.
量一量
量出四个内角的度数
算一算
计算出这四个内角的和.
A
B
c
D
E
A
B
c
D
E
A
B
c
D
小结:都是从同一个点出发和各顶点相连,把四边形问题转化为熟悉的三角形问题来解决。
这三种方法有什么共同点呢?
2×180°=360°
3×18 0-180°=360°
4×18 0-360°=360°
.
.
.
探索多边形的内角和
这个五边形的内角和应该怎么求呢?
你有几种方法呢?
A
C
D
E
B
A
C
E
D
B
展示:
内角和=3 × 180°
=540 °
.
你能仿照五边形分割成三角形的方法,选出你认为最简单的一种分割六边形并求其内角和吗?
A
B
C
D
E
F
.
多边形
的边数
图 形
分割出的三角形的个数
多边形的
内 角 和
3
4
5
------
------
------
------
n
n-2
1
2
3
1×180?
2×180?
3×180?
(n-2)×180?
综上所述,设多边形的边数为n,
则 n边形的内角和等于
(n-2)×180?
?
知道了多边形的内角和,它可以解决哪些问题呢?
?
1、已知边数,求内角和
2、已知内角和求边数
1.十二边形的内角和等于______度.
2.已知多边形的每个内角都是135度,则这个
多边形是_______.
3.一个多边形当边数增加1时,它的内角和
增加 度。
4.过多边形的一个顶点可以引7条对角线,那么这个多边形的内角和是 。
1800
八边形
180
1440°
1、一个多边形的内角和等于900°,它是几边形?
2、求下列图形中 x的值
如果一个四边形的一组对角互补,
那么另一组对角有什么关系?
解:
如图,四边形ABCD中,
∠A+ ∠C =180°
∠A+∠B+∠C+∠D=(4-2) ×180 °
= 360 °
因为
∠B+∠D
= 360°-(∠A+∠C)
= 360°- 180°
=180°
这就是说:如果四边形一组对角互补,那么另一组对角也互补.
所以
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
用形状、大小完全相同的任意四边形可拼成一块无空隙的地板,你知道这是为什么吗?
1、n边形的内角和等于(n-2)×180°,公式的应用;
2、转化的方法.
这节课我们学到了什么?
A
C
D
E
B
.
2、你能用多边形的内角和公式推导多边形的外角和吗?
1、你能用左图推导多边形的内角和公式吗?
如图,在正五边形ABCDE中,连接BE,求∠BED的度数.
解:由题意得
AB=AE,所以∠AEB= (180°–∠A)=36°,
所以∠BED=∠AED–∠AEB=108°–36°=72°.
巩固练习
1.已知正多边形的一个外角等于40°,那么这个正多边形的边数为( )
A.6 B.7 C.8 D.9
解析:正多边形的一个外角等于40°,且外角和为360°,则这个正多边形的边数是:360°÷40°=9.
D
连接中考
2.若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是_____.
解析:设多边形的边数为n,根据题意,得
(n–2)?180=3×360,
解得 n=8.
则这个多边形的边数是8.
8
连接中考
1.判断.
(1)当多边形边数增加时,它的内角和也随着增加.( )
(2)当多边形边数增加时,它的外角和也随着增加.( )
(3)三角形的外角和与八边形的外角和相等. ( )
2.一个多边形的每一个外角都是36°,则这个多边形的边数是 .
基础巩固题
10
课堂检测
3. 如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是________米.
150
课堂检测
4. 一个多边形从一个顶点可引对角线3条,这个多边形
内角和等于( )
A. 360° B. 540 °
C. 720 ° D. 900 °
B
课堂检测
一个多边形的内角和为1800°,截去一个角后,求得到的多边形的内角和.
能力提升题
课堂检测
如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
解:如图,
∵∠3+∠4=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7
=∠1+∠2+∠8+∠9+∠5+∠6+∠7
=五边形的内角和
=540°.
8
9
拓广探索题
课堂检测
多边形的内角和
内角和计算公式
(n–2) × 180 °(n ≥3的整数)① 边数增加1,内角和增加180°;②内角和是180°的整倍数.
外角和
多边形的外角和等于360°
特别注意:与边数无关.
正多
边形
内角= ,外角=
课堂小结
