2020-2021学年人教版数学八年级上册12.1全等三角形课件(共29张PPT)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册12.1全等三角形课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 07:23:46 | ||
图片预览





文档简介
新课标人教版八年级上册
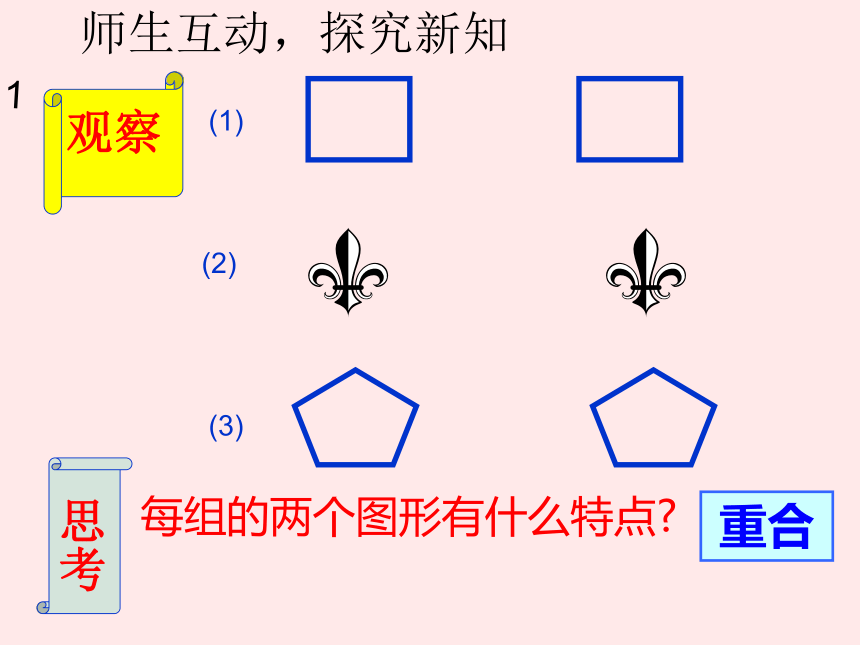
1、下列各组图形形状与大小有什么特点?
2、同一张底片洗出大小相同的照片有何特点?
答:能完全重合在一起。
重合
(1)
(2)
(3)
思考
每组的两个图形有什么特点?
观察
重合
师生互动,探究新知
1
能够完全重合的两个图形叫做
全等形:
全等图形的特征
全等图形的形状和大小都相同
小结:
你能再举出生活中的一些实际例子吗?
A
B
C
E
D
F
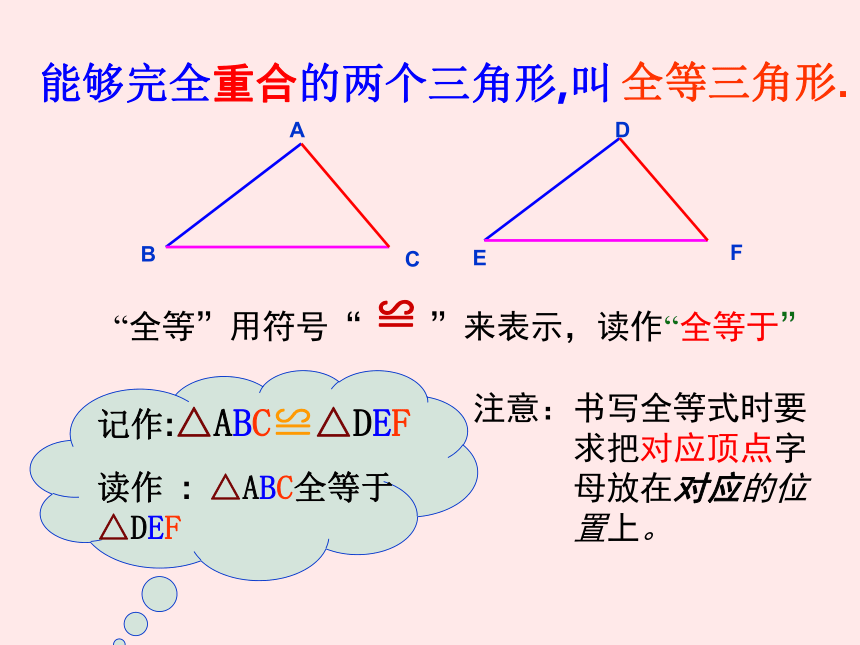
能够完全重合的两个三角形,叫
全等三角形.
记作:△ABC≌△DEF
读作 : △ABC全等于 △DEF
注意:书写全等式时要
求把对应顶点字
母放在对应的位
置上。
“全等”用符号“ ”来表示,读作
≌
“全等于”
A
B
C
D
E
F
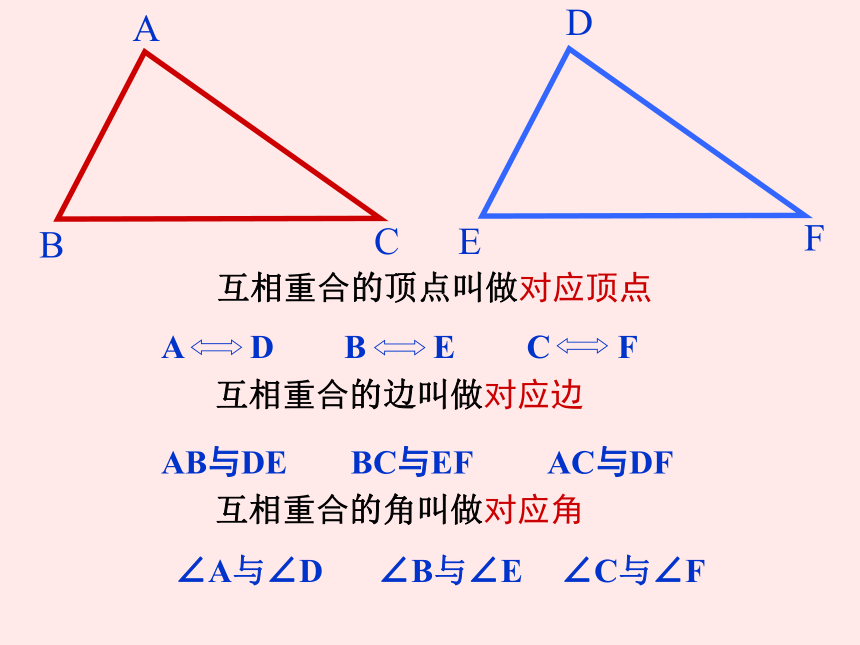
互相重合的边叫做对应边
互相重合的顶点叫做对应顶点
互相重合的角叫做对应角
A D
B E
C F
AB与DE
BC与EF
AC与DF
∠A与∠D
∠B与∠E
∠C与∠F
A
B
C
E
D
F
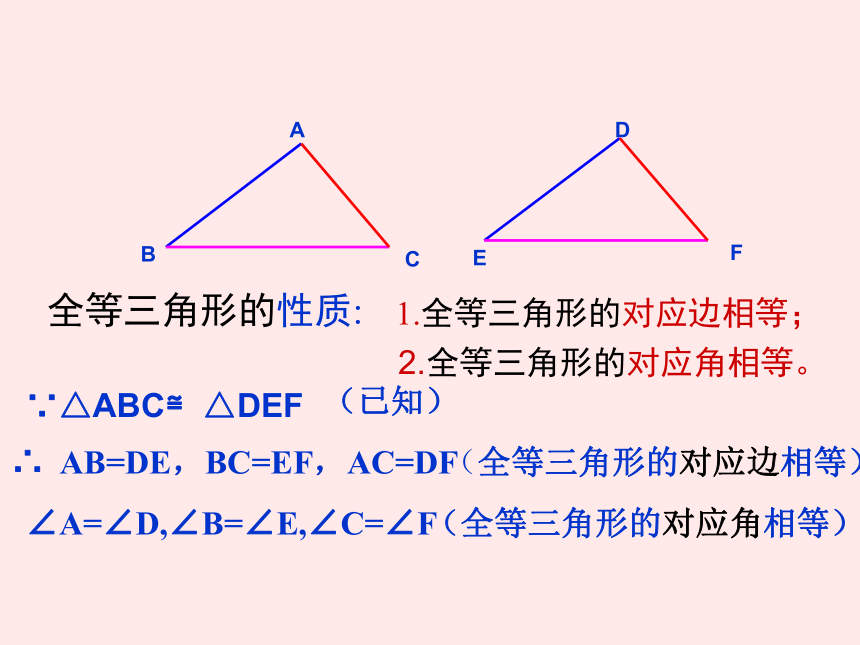
全等三角形的性质:
1.全等三角形的对应边相等;
2.全等三角形的对应角相等。
∵△ABC≌△DEF
(已知)
∴ AB=DE,BC=EF,AC=DF
(全等三角形的对应边相等)
∠A=∠D,∠B=∠E,∠C=∠F
(全等三角形的对应角相等)
观察,下列各组的两个全等三角形,进行小组讨论,看看谁能在最短的时间内找到他们的对应边或对应角?谈谈你们小组的方法!
(1)
A
B
D
E
F
c
平 移
A
B
C
(2)这两个全等三角形的对应边、
对应角呢?
D
公共边是对应边
翻折
A
B
C
A
C
(3)这两个全等三角形的对应边、
对应角呢?
D
E
对顶角也是对应角
旋转
请指出全等△ ABE 和△ ACF的
对应边和对应角!
(4)、找朋友
公共角是对应角
B
A
C
N
P
M
A
C
B
D
E
A
B
C
D
C
B
图1
图2
图3
图4
一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等。
A
D
E
观察
学以致用,落实新知
1、判断
(1)两个全等形一定能够重合( )
(2)两个图形全等,所有对应元素都相等( )
(3)三个角对应相等的两个三角形全等( )
(4)两个三角形全等,对应顶点所在的角一定是
对应角,对应边所夹的角一定是对应角,
对应角所对的边也是对应边。 ( )
2、如图所示,△ABC≌△DCB,则观察图形一定有下
列关系成立:
⑴ AB = ___,AC = ____;
⑵∠A = ____,∠ABC = _____,
∠ACB =___.
3、如图△ ABD ≌ △CDB,若AB=3,AD=5,BD=6,则BC= ,CD= 。
A
B
D
C
变式练习,拓展能力
1、如图△ABD≌ △EBC,AB=3cm,BC=5cm,求DE的长
A
B
C
D
E
2:如图,△ABC≌△AEC,∠B=30°,∠ACB=85°.求出△AEC各内角的度数 .
B
C
E
E
A
1、能够完全重合的两个图形叫做全等形
2、能够完全重合的两个三角形叫做全等三角形
全等三角形的性质:
全等三角形的对应角相等
全等三角形的对应边相等
反思小结,观点提炼
回忆这节课,学习了全等三角形的哪些知识?
如图,△ABC ≌△CDA,AB 与CD,BC 与DA 是对应边,则下列结论错误的是( ).
A. ∠ BAC =∠ DCA ;
B. AB∥DC ;
C.∠ BCA =∠ DCA ;
D. BC∥DA .
C
A
B
C
D
巩固练习
解析:∵△ABF与△DCE全等,点A与点D,点B与点C是对应顶点.
∴∠DCE=∠B.
1. 如图所示,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )
A.∠B B.∠A C.∠EMF D.∠AFB
A
连接中考
解析:先根据三角形外角的性质求出
∠ ACA'=∠A+∠B=27°+40°=67°.
再由△ABC绕点C按顺时针方向旋转至△A'B'C,得到
△ABC≌△A'B'C,
∴∠ACB=∠A'CB'.
∴∠ACB–∠B'CA=∠A'CB'–∠B'CA, 即∠BCB'=∠ACA'. ∴∠BCB'=67°.
∴∠ACB'=180°–∠ACA'–∠BCB'=180°–67°–67°=46°.
2. 如图所示,将△ABC绕点C按顺时针方向旋转至△A'B'C,使点A'落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB'为_______度.?
46
连接中考
1.能够 的两个图形叫做全等形.两个三角形 重合时,互相 的顶点叫做对应顶点.记两个全等三角形时,通常把表示 顶点的字母写在 的位置上.
重合
重合
相对应
2.如图,△ABC≌ △ADE,若∠D=∠B,
∠C= ∠AED,则∠DAE= ; ∠DAB= .
∠BAC
∠EAC
A
B
C
D
E
课堂检测
基础巩固题
对应顶点
3.如图,△ABC≌△BAD,如果AB=5cm, BD=4cm,AD=6cm,那么BC的长是( )
A.6cm B.5cm
C.4cm D.无法确定
4.在上题中,∠CAB的对应角是( )
A.∠DAB B.∠DBA C.∠DBC D.∠CAD
A
O
C
D
B
A
B
课堂检测
如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )
A.△ABD 和△CDB 的面积相等
B.△ABD 和△CDB 的周长相等
C.∠A +∠ABD =∠C +∠CBD
D.AD∥BC,且AD = BC
C
能力提升题
课堂检测
如图,△ABC ≌△AED,AB是△ABC 的最大边,AE是△AED的最大边,∠BAC 与∠ EAD是对应角,且∠BAC=25°,∠B= 35°,AB =3cm,BC =1cm,求出∠E, ∠ ADE 的度数和线段DE,AE 的长度.
B
C
E
D
A
解:∵ △ABC ≌△AED,(已知)
∴∠E= ∠B = 35°,(全等三角形对应角相等)
∠ADE =∠ACB =180°–25°–35°=120 °, (全等三角形对应角相等)
DE = BC =1cm, AE = AB =3cm.
(全等三角形对应边相等)
拓广探索题
课堂检测
摆一摆:利用平移,翻折,旋转等变换所得到的三角形与原三角形组成各种各样新的图形,你还能拼出什么不同的造型吗?比一比看谁更有创意!
课堂检测
拼接的图形展示
课堂检测
全等
三角形
定义
能够完全重合的两个三角形叫做全等三角形
基本性质
对应边相等
对应角相等
对应元素确定方法
对应边
对应角
长对长,短对短,中对中
公共边一定是对应边
大角对大角,小角对小角
公共角一定是对应角
对顶角一定是对应角
课堂小结
1、下列各组图形形状与大小有什么特点?
2、同一张底片洗出大小相同的照片有何特点?
答:能完全重合在一起。
重合
(1)
(2)
(3)
思考
每组的两个图形有什么特点?
观察
重合
师生互动,探究新知
1
能够完全重合的两个图形叫做
全等形:
全等图形的特征
全等图形的形状和大小都相同
小结:
你能再举出生活中的一些实际例子吗?
A
B
C
E
D
F
能够完全重合的两个三角形,叫
全等三角形.
记作:△ABC≌△DEF
读作 : △ABC全等于 △DEF
注意:书写全等式时要
求把对应顶点字
母放在对应的位
置上。
“全等”用符号“ ”来表示,读作
≌
“全等于”
A
B
C
D
E
F
互相重合的边叫做对应边
互相重合的顶点叫做对应顶点
互相重合的角叫做对应角
A D
B E
C F
AB与DE
BC与EF
AC与DF
∠A与∠D
∠B与∠E
∠C与∠F
A
B
C
E
D
F
全等三角形的性质:
1.全等三角形的对应边相等;
2.全等三角形的对应角相等。
∵△ABC≌△DEF
(已知)
∴ AB=DE,BC=EF,AC=DF
(全等三角形的对应边相等)
∠A=∠D,∠B=∠E,∠C=∠F
(全等三角形的对应角相等)
观察,下列各组的两个全等三角形,进行小组讨论,看看谁能在最短的时间内找到他们的对应边或对应角?谈谈你们小组的方法!
(1)
A
B
D
E
F
c
平 移
A
B
C
(2)这两个全等三角形的对应边、
对应角呢?
D
公共边是对应边
翻折
A
B
C
A
C
(3)这两个全等三角形的对应边、
对应角呢?
D
E
对顶角也是对应角
旋转
请指出全等△ ABE 和△ ACF的
对应边和对应角!
(4)、找朋友
公共角是对应角
B
A
C
N
P
M
A
C
B
D
E
A
B
C
D
C
B
图1
图2
图3
图4
一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等。
A
D
E
观察
学以致用,落实新知
1、判断
(1)两个全等形一定能够重合( )
(2)两个图形全等,所有对应元素都相等( )
(3)三个角对应相等的两个三角形全等( )
(4)两个三角形全等,对应顶点所在的角一定是
对应角,对应边所夹的角一定是对应角,
对应角所对的边也是对应边。 ( )
2、如图所示,△ABC≌△DCB,则观察图形一定有下
列关系成立:
⑴ AB = ___,AC = ____;
⑵∠A = ____,∠ABC = _____,
∠ACB =___.
3、如图△ ABD ≌ △CDB,若AB=3,AD=5,BD=6,则BC= ,CD= 。
A
B
D
C
变式练习,拓展能力
1、如图△ABD≌ △EBC,AB=3cm,BC=5cm,求DE的长
A
B
C
D
E
2:如图,△ABC≌△AEC,∠B=30°,∠ACB=85°.求出△AEC各内角的度数 .
B
C
E
E
A
1、能够完全重合的两个图形叫做全等形
2、能够完全重合的两个三角形叫做全等三角形
全等三角形的性质:
全等三角形的对应角相等
全等三角形的对应边相等
反思小结,观点提炼
回忆这节课,学习了全等三角形的哪些知识?
如图,△ABC ≌△CDA,AB 与CD,BC 与DA 是对应边,则下列结论错误的是( ).
A. ∠ BAC =∠ DCA ;
B. AB∥DC ;
C.∠ BCA =∠ DCA ;
D. BC∥DA .
C
A
B
C
D
巩固练习
解析:∵△ABF与△DCE全等,点A与点D,点B与点C是对应顶点.
∴∠DCE=∠B.
1. 如图所示,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )
A.∠B B.∠A C.∠EMF D.∠AFB
A
连接中考
解析:先根据三角形外角的性质求出
∠ ACA'=∠A+∠B=27°+40°=67°.
再由△ABC绕点C按顺时针方向旋转至△A'B'C,得到
△ABC≌△A'B'C,
∴∠ACB=∠A'CB'.
∴∠ACB–∠B'CA=∠A'CB'–∠B'CA, 即∠BCB'=∠ACA'. ∴∠BCB'=67°.
∴∠ACB'=180°–∠ACA'–∠BCB'=180°–67°–67°=46°.
2. 如图所示,将△ABC绕点C按顺时针方向旋转至△A'B'C,使点A'落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB'为_______度.?
46
连接中考
1.能够 的两个图形叫做全等形.两个三角形 重合时,互相 的顶点叫做对应顶点.记两个全等三角形时,通常把表示 顶点的字母写在 的位置上.
重合
重合
相对应
2.如图,△ABC≌ △ADE,若∠D=∠B,
∠C= ∠AED,则∠DAE= ; ∠DAB= .
∠BAC
∠EAC
A
B
C
D
E
课堂检测
基础巩固题
对应顶点
3.如图,△ABC≌△BAD,如果AB=5cm, BD=4cm,AD=6cm,那么BC的长是( )
A.6cm B.5cm
C.4cm D.无法确定
4.在上题中,∠CAB的对应角是( )
A.∠DAB B.∠DBA C.∠DBC D.∠CAD
A
O
C
D
B
A
B
课堂检测
如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )
A.△ABD 和△CDB 的面积相等
B.△ABD 和△CDB 的周长相等
C.∠A +∠ABD =∠C +∠CBD
D.AD∥BC,且AD = BC
C
能力提升题
课堂检测
如图,△ABC ≌△AED,AB是△ABC 的最大边,AE是△AED的最大边,∠BAC 与∠ EAD是对应角,且∠BAC=25°,∠B= 35°,AB =3cm,BC =1cm,求出∠E, ∠ ADE 的度数和线段DE,AE 的长度.
B
C
E
D
A
解:∵ △ABC ≌△AED,(已知)
∴∠E= ∠B = 35°,(全等三角形对应角相等)
∠ADE =∠ACB =180°–25°–35°=120 °, (全等三角形对应角相等)
DE = BC =1cm, AE = AB =3cm.
(全等三角形对应边相等)
拓广探索题
课堂检测
摆一摆:利用平移,翻折,旋转等变换所得到的三角形与原三角形组成各种各样新的图形,你还能拼出什么不同的造型吗?比一比看谁更有创意!
课堂检测
拼接的图形展示
课堂检测
全等
三角形
定义
能够完全重合的两个三角形叫做全等三角形
基本性质
对应边相等
对应角相等
对应元素确定方法
对应边
对应角
长对长,短对短,中对中
公共边一定是对应边
大角对大角,小角对小角
公共角一定是对应角
对顶角一定是对应角
课堂小结
