2020-2021学年人教版数学八年级上册12.3角平分线的性质(共22张PPT)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册12.3角平分线的性质(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 799.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 07:27:36 | ||
图片预览





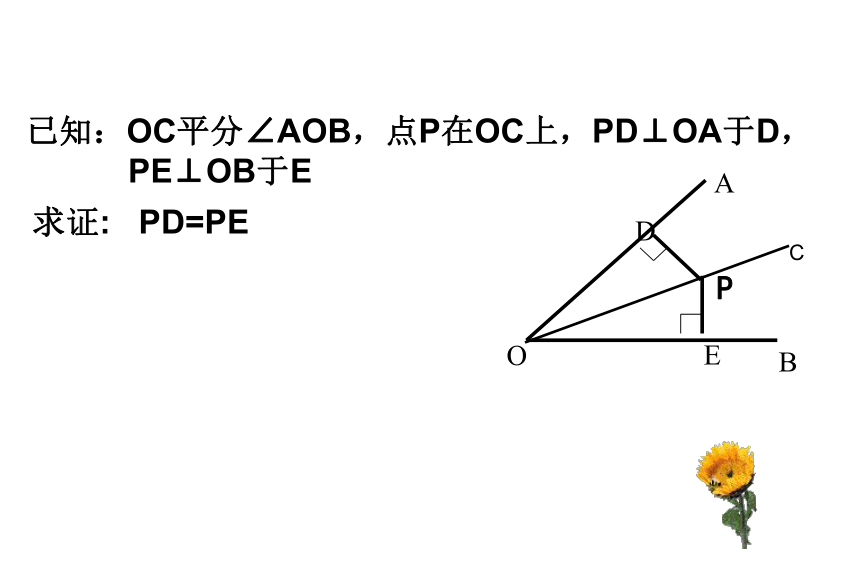
文档简介
1、“两直线平行,内错角相等”是平行线的______,它的已知条件是____结论是_______。
“内错角相等,两直线平行”是平行线的______,它的已知条件是____结论是_______。
2、角平分线的定义:从一个角的顶点出发,把这个角分成_______两个角的射线叫做这个角的角平分线。
3、点到直线的距离是这个点到这条直线的______的长度。
● A
D
●A
O
C
D
12.3 角平分线的性质
学习目标
知识与技能:
1、能够利用三角形全等,证明角平分线的性质和判定.(重点)
2、会用尺规作已知角的平分线。(重点)
3、能对角平分线性质进行简单的推理,解决一些实际问题。(难点)
过程与方法:
经历画图、猜测、归纳、发现和解决问题的过程,总结和探索几何规律的方法。
情感态度与价值观:
经历在现实情境中认识角平分线的数学活动过程,感受图形世界的丰富多彩,增强审美意识,激发求知欲。
C
自学指导
5分钟认真阅读课本48-49页思考以上的内容,
回答下列问题:
1、思考中为什么AE是这个角的平分线?
2、亲自用尺规作图作一个角的平分线,并思考在作法的第二步中,去掉“大于 MN的长”这个条件行吗?
3、角的平分线的性质是什么?如何证明?
4、对于一个几何命题进行证明
的一般步骤是什么?
证明几何中命题的步骤
1.明确命题中的已知和求证。
2 .根据题意,画出图形,并用数学符号表示已知和求证。
3.经过分析,找出由已知推出求证的途径,写出证明过程。
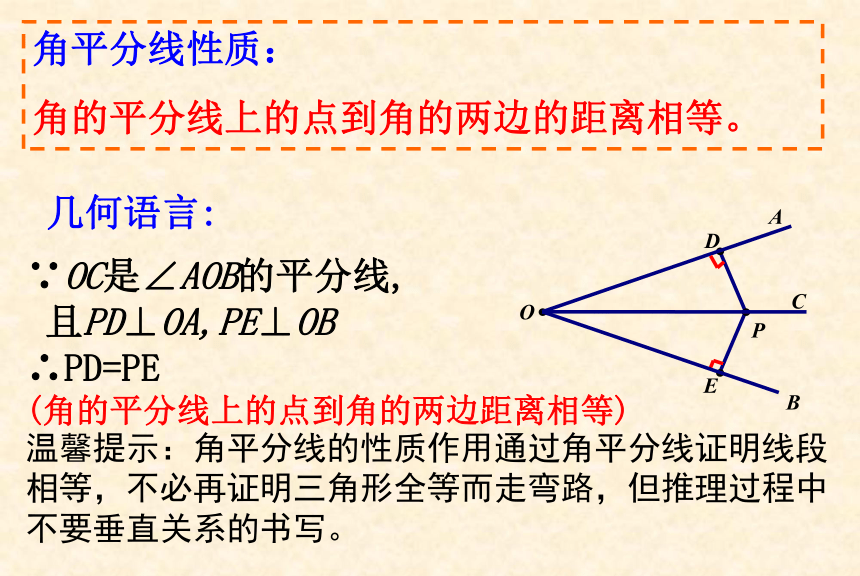
已知:OC平分∠AOB,点P在OC上,PD⊥OA于D,
PE⊥OB于E
求证: PD=PE
A
O
B
E
D
P
C
∵OC是∠AOB的平分线,
且PD⊥OA,PE⊥OB
∴PD=PE
(角的平分线上的点到角的两边距离相等)
几何语言:
角平分线性质:
角的平分线上的点到角的两边的距离相等。
E
D
O
A
B
P
C
温馨提示:角平分线的性质作用通过角平分线证明线段相等,不必再证明三角形全等而走弯路,但推理过程中不要垂直关系的书写。
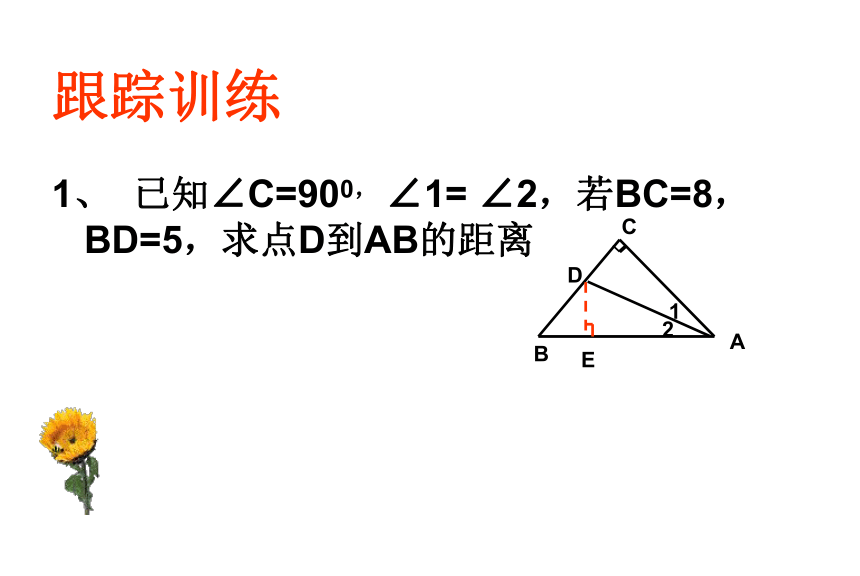
跟踪训练
1、 已知∠C=900, ∠1= ∠2,若BC=8,BD=5,求点D到AB的距离
1
2
A
B
C
D
E
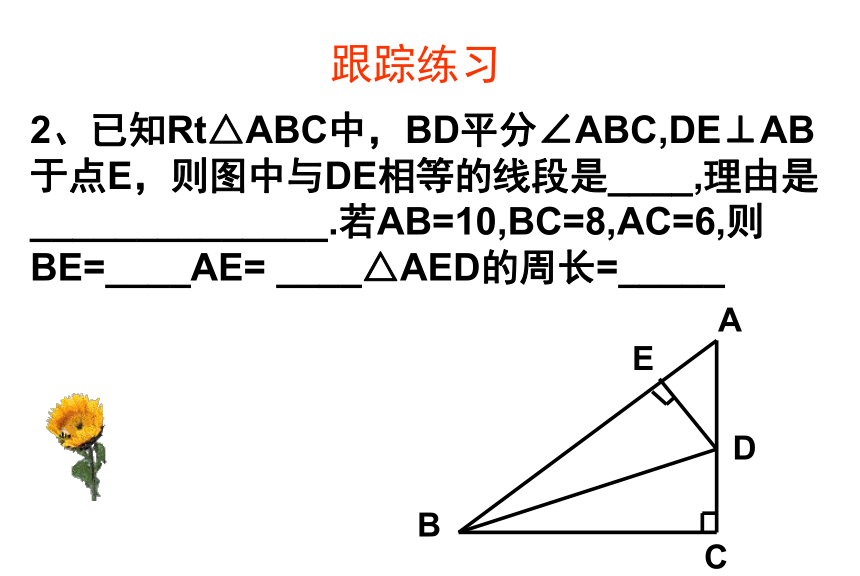
2、已知Rt△ABC中,BD平分∠ABC,DE⊥AB于点E,则图中与DE相等的线段是____,理由是______________.若AB=10,BC=8,AC=6,则BE=____AE= ____△AED的周长=_____
B
E
A
D
C
跟踪练习
自学指导2
3分钟阅读49页思考到50页练习以上的内容,回答下列问题:
1、完成49页的思考。
2、角的平分线的判定:角的____到角的两边的_____相等的点在角的_________如何证明?
C
3、认真阅读50页的例题,它利用的是什么?并完成云状图。
已知:PD OA于D,PE OB于E,且PD=PE
求证:P在角平分线OC上
C
温馨提示:角平分线的判定作用:通过线段相等证明是否是角平分线
例题平行练习:
如图,△ABC的∠B 的平分线 BD 与∠C 的外角的平分线 CE 相交于点 P.
求证:点 P 到三边 AB , BC , CA 所在直线的距离相等.
例题平行练习2:
如图,三条公路相交,现在要修建一加油站,使加油站到三条公路的距离相等,问加油站该选在什么位置上?
角的平分线的判定:角的内部到角的两边的距离相等的点在角的平分线上。
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
用数学语言表示为:
角的平分线的性质:角的平分线上的点到角的两边的距离相等.
用数学语言表示为:
∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上
∴ QD=QE
如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A.30° B.35° C.45° D.60°
B
N
连接中考
2.△ABC中, ∠C=90°,AD平分∠CAB,且BC=8,BD=5,则点D到AB的距离是 .
A
B
C
D
3
E
1. 如图,DE⊥AB,DF⊥BG,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= .
60
BF
E
B
D
F
A
C
G
课堂检测
基础巩固题
3. 用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
SSS
ASA
AAS
角平分线上的点到角两边的距离相等
A
B
M
N
C
O
A
课堂检测
4.如图,OP平分∠AOB,PC⊥OA,PD⊥OB,垂足分别是C,D,下列结论中错误的是( )
A.PC=PD B. OC=OD
C. ∠CPO=∠DPO D. OC=PC
D
5. 如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=7,DE=2,AB=4,则AC的长是( )
A.6 B.5 C.4 D.3
D
B
C
E
A
D
F
课堂检测
E
D
C
B
A
6
8
10
1. 在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,则:
(1)哪条线段与DE相等?为什么?
(2)若AB=10,BC=8,AC=6,求BE,AE的长和△AED 的周长.
解:(1)DC=DE.
理由如下:角平分线上的点到角两边的距离相等.
(2)在Rt△CDB和Rt△EDB中,DC=DE,DB=DB,
∴Rt△CDB≌Rt△EDB(HL),
∴BE=BC=8.
∴ AE=AB–BE=2.
∴△AED的周长=AE+ED+DA=2+6=8.
能力提升题
C
D
课堂检测
2.如图所示,D是∠ACG的平分线上的一点.DE⊥AC,DF⊥CG,垂足分别为E,F. 求证:CE=CF.
证明:∵CD是∠ACG的平分线,DE⊥AC,DF⊥CG,
∴DE=DF.
在Rt△CDE和Rt△CDF中,
∴Rt△CDE≌Rt△CDF(HL),
∴CE=CF.
课堂检测
如图,已知AD∥BC,P是∠BAD与∠ABC的平分线的交点,PE⊥AB于E,且PE=3,求AD与BC之间的距离.
解:过点P作MN⊥AD于点M,交BC于点N.
∵ AD∥BC,
∴ MN⊥BC,MN的长即为AD与BC之间的距离.
∵ AP平分∠BAD, PM⊥AD , PE⊥AB,
∴ PM= PE.
同理, PN= PE.
∴ PM= PN= PE=3.
∴ MN=6.即AD与BC之间的距离为6.
拓广探索题
课堂检测
角平分线
尺规作图
属于基本作图,必须熟练掌握
性质定理
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等
辅助线
添加
过角平分线上一点向两边作垂线段
课堂小结
为证明线段相等提供了又一途径
“内错角相等,两直线平行”是平行线的______,它的已知条件是____结论是_______。
2、角平分线的定义:从一个角的顶点出发,把这个角分成_______两个角的射线叫做这个角的角平分线。
3、点到直线的距离是这个点到这条直线的______的长度。
● A
D
●A
O
C
D
12.3 角平分线的性质
学习目标
知识与技能:
1、能够利用三角形全等,证明角平分线的性质和判定.(重点)
2、会用尺规作已知角的平分线。(重点)
3、能对角平分线性质进行简单的推理,解决一些实际问题。(难点)
过程与方法:
经历画图、猜测、归纳、发现和解决问题的过程,总结和探索几何规律的方法。
情感态度与价值观:
经历在现实情境中认识角平分线的数学活动过程,感受图形世界的丰富多彩,增强审美意识,激发求知欲。
C
自学指导
5分钟认真阅读课本48-49页思考以上的内容,
回答下列问题:
1、思考中为什么AE是这个角的平分线?
2、亲自用尺规作图作一个角的平分线,并思考在作法的第二步中,去掉“大于 MN的长”这个条件行吗?
3、角的平分线的性质是什么?如何证明?
4、对于一个几何命题进行证明
的一般步骤是什么?
证明几何中命题的步骤
1.明确命题中的已知和求证。
2 .根据题意,画出图形,并用数学符号表示已知和求证。
3.经过分析,找出由已知推出求证的途径,写出证明过程。
已知:OC平分∠AOB,点P在OC上,PD⊥OA于D,
PE⊥OB于E
求证: PD=PE
A
O
B
E
D
P
C
∵OC是∠AOB的平分线,
且PD⊥OA,PE⊥OB
∴PD=PE
(角的平分线上的点到角的两边距离相等)
几何语言:
角平分线性质:
角的平分线上的点到角的两边的距离相等。
E
D
O
A
B
P
C
温馨提示:角平分线的性质作用通过角平分线证明线段相等,不必再证明三角形全等而走弯路,但推理过程中不要垂直关系的书写。
跟踪训练
1、 已知∠C=900, ∠1= ∠2,若BC=8,BD=5,求点D到AB的距离
1
2
A
B
C
D
E
2、已知Rt△ABC中,BD平分∠ABC,DE⊥AB于点E,则图中与DE相等的线段是____,理由是______________.若AB=10,BC=8,AC=6,则BE=____AE= ____△AED的周长=_____
B
E
A
D
C
跟踪练习
自学指导2
3分钟阅读49页思考到50页练习以上的内容,回答下列问题:
1、完成49页的思考。
2、角的平分线的判定:角的____到角的两边的_____相等的点在角的_________如何证明?
C
3、认真阅读50页的例题,它利用的是什么?并完成云状图。
已知:PD OA于D,PE OB于E,且PD=PE
求证:P在角平分线OC上
C
温馨提示:角平分线的判定作用:通过线段相等证明是否是角平分线
例题平行练习:
如图,△ABC的∠B 的平分线 BD 与∠C 的外角的平分线 CE 相交于点 P.
求证:点 P 到三边 AB , BC , CA 所在直线的距离相等.
例题平行练习2:
如图,三条公路相交,现在要修建一加油站,使加油站到三条公路的距离相等,问加油站该选在什么位置上?
角的平分线的判定:角的内部到角的两边的距离相等的点在角的平分线上。
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
用数学语言表示为:
角的平分线的性质:角的平分线上的点到角的两边的距离相等.
用数学语言表示为:
∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上
∴ QD=QE
如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A.30° B.35° C.45° D.60°
B
N
连接中考
2.△ABC中, ∠C=90°,AD平分∠CAB,且BC=8,BD=5,则点D到AB的距离是 .
A
B
C
D
3
E
1. 如图,DE⊥AB,DF⊥BG,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= .
60
BF
E
B
D
F
A
C
G
课堂检测
基础巩固题
3. 用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
SSS
ASA
AAS
角平分线上的点到角两边的距离相等
A
B
M
N
C
O
A
课堂检测
4.如图,OP平分∠AOB,PC⊥OA,PD⊥OB,垂足分别是C,D,下列结论中错误的是( )
A.PC=PD B. OC=OD
C. ∠CPO=∠DPO D. OC=PC
D
5. 如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=7,DE=2,AB=4,则AC的长是( )
A.6 B.5 C.4 D.3
D
B
C
E
A
D
F
课堂检测
E
D
C
B
A
6
8
10
1. 在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,则:
(1)哪条线段与DE相等?为什么?
(2)若AB=10,BC=8,AC=6,求BE,AE的长和△AED 的周长.
解:(1)DC=DE.
理由如下:角平分线上的点到角两边的距离相等.
(2)在Rt△CDB和Rt△EDB中,DC=DE,DB=DB,
∴Rt△CDB≌Rt△EDB(HL),
∴BE=BC=8.
∴ AE=AB–BE=2.
∴△AED的周长=AE+ED+DA=2+6=8.
能力提升题
C
D
课堂检测
2.如图所示,D是∠ACG的平分线上的一点.DE⊥AC,DF⊥CG,垂足分别为E,F. 求证:CE=CF.
证明:∵CD是∠ACG的平分线,DE⊥AC,DF⊥CG,
∴DE=DF.
在Rt△CDE和Rt△CDF中,
∴Rt△CDE≌Rt△CDF(HL),
∴CE=CF.
课堂检测
如图,已知AD∥BC,P是∠BAD与∠ABC的平分线的交点,PE⊥AB于E,且PE=3,求AD与BC之间的距离.
解:过点P作MN⊥AD于点M,交BC于点N.
∵ AD∥BC,
∴ MN⊥BC,MN的长即为AD与BC之间的距离.
∵ AP平分∠BAD, PM⊥AD , PE⊥AB,
∴ PM= PE.
同理, PN= PE.
∴ PM= PN= PE=3.
∴ MN=6.即AD与BC之间的距离为6.
拓广探索题
课堂检测
角平分线
尺规作图
属于基本作图,必须熟练掌握
性质定理
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等
辅助线
添加
过角平分线上一点向两边作垂线段
课堂小结
为证明线段相等提供了又一途径
