2020-2021学年人教版数学八年级上册13.2画轴对称图形课件(34张)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册13.2画轴对称图形课件(34张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 00:00:00 | ||
图片预览






文档简介
第十三章 轴对称
13.2 画轴对称图形
一、什么是轴对称图形?什么叫两个图形成轴对称?
1、如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
2、对于两个图形,如果沿一条直线对折后,它们能完全重合,
那么这两个图形成轴对称,这条直线就是对称轴.
二、轴对称主要有哪些性质?
1、关于某条直线对称的两个图形是全等形;
2、如果两个图形关于某直线对称,那么对应点所连的线段被对称轴垂直平分;
3、成轴对称的两个图形的对应线段相等,对应角相等.
知识回顾
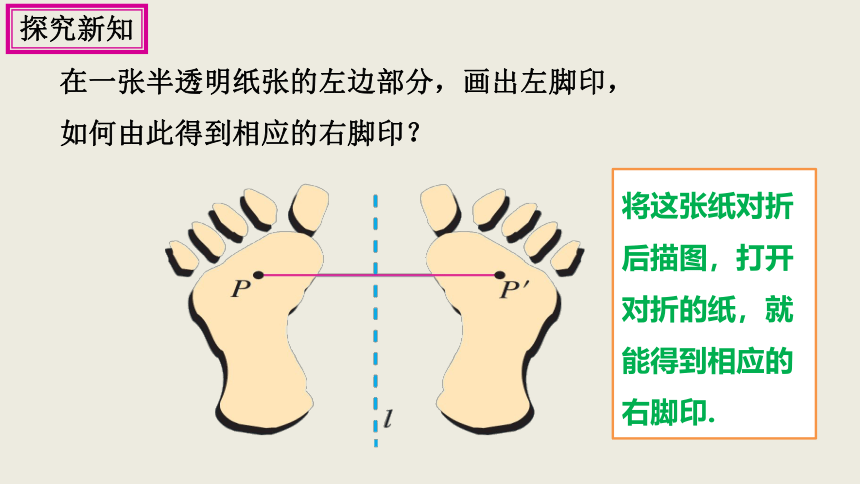
在一张半透明纸张的左边部分,画出左脚印,如何由此得到相应的右脚印?
探究新知
将这张纸对折后描图,打开对折的纸,就能得到相应的右脚印.
(1)画出的轴对称图形的形状、大小和原图形有什么
关系?
(2)画出的轴对称图形的点与原图形上的点有什么关系?
(3)对应点所连线段与对称轴有什么关系?
一个平面图形和与它成轴对称的另一个图形之间有什么关系?
答:由一个平面图形可以得到与它关于一条直线l 对称
的图形,这个图形与原图形的形状、大小完全相同;
答:新图形上的每一点都是原图形上的某一点关于直线 l 的对称点;
答:连接任意一对对应点的线段被对称轴垂直平分.
探究新知
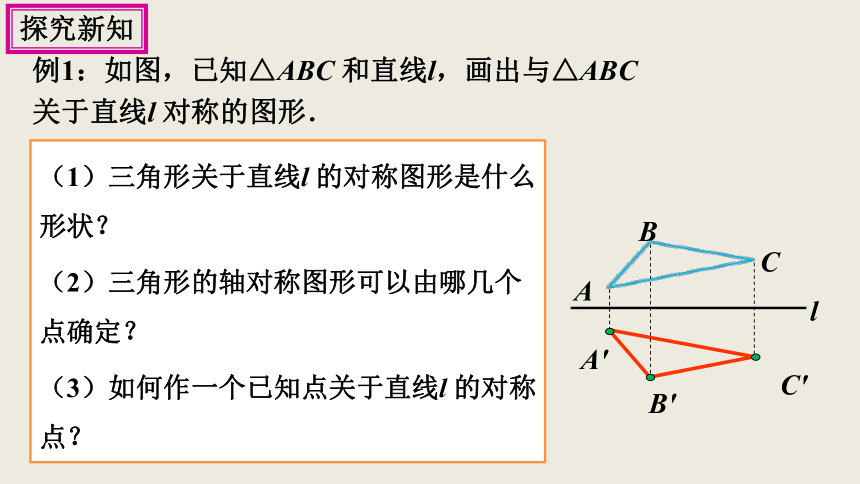
(1)三角形关于直线l 的对称图形是什么形状?
(2)三角形的轴对称图形可以由哪几个点确定?
(3)如何作一个已知点关于直线l 的对称点?
A
B
C
l
A′
B′
C′
例1:如图,已知△ABC 和直线l,画出与△ABC
关于直线l 对称的图形.
探究新知
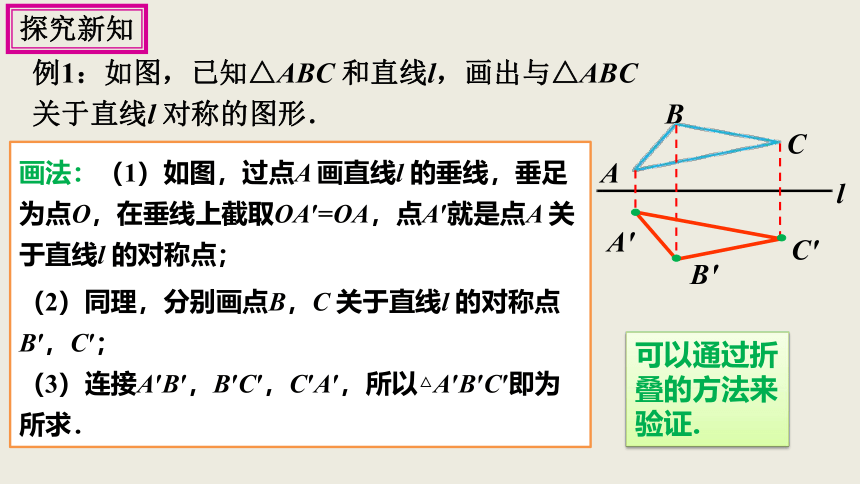
画法:(1)如图,过点A 画直线l 的垂线,垂足为点O,在垂线上截取OA′=OA,点A′就是点A 关于直线l 的对称点;
(2)同理,分别画点B,C 关于直线l 的对称点B′,C′;
(3)连接A′B′,B′C′,C′A′,所以△A′B′C′即为所求.
A
B
C
l
A′
B′
C′
例1:如图,已知△ABC 和直线l,画出与△ABC
关于直线l 对称的图形.
探究新知
可以通过折叠的方法来验证.
已知一个几何图形和一条直线,说一说画一个与该图形关于这条直线对称的图形的一般方法.
几何图形都可以看作由点组成.
对于某些图形,只要画出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
探究归纳
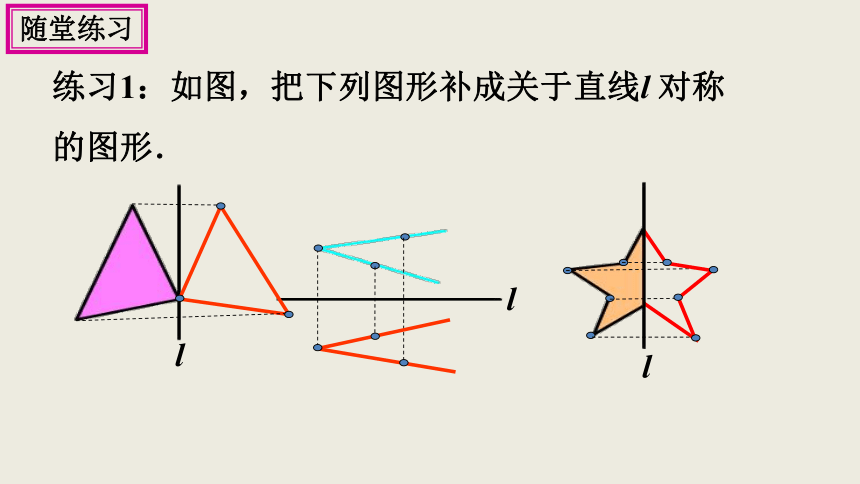
练习1:如图,把下列图形补成关于直线l 对称的图形.
l
l
l
随堂练习
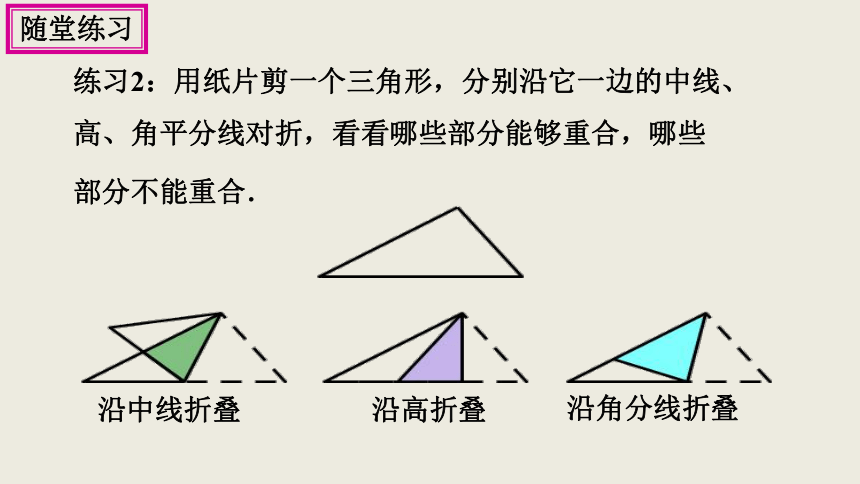
练习2:用纸片剪一个三角形,分别沿它一边的中线、高、角平分线对折,看看哪些部分能够重合,哪些
部分不能重合.
沿角分线折叠
沿高折叠
沿中线折叠
随堂练习
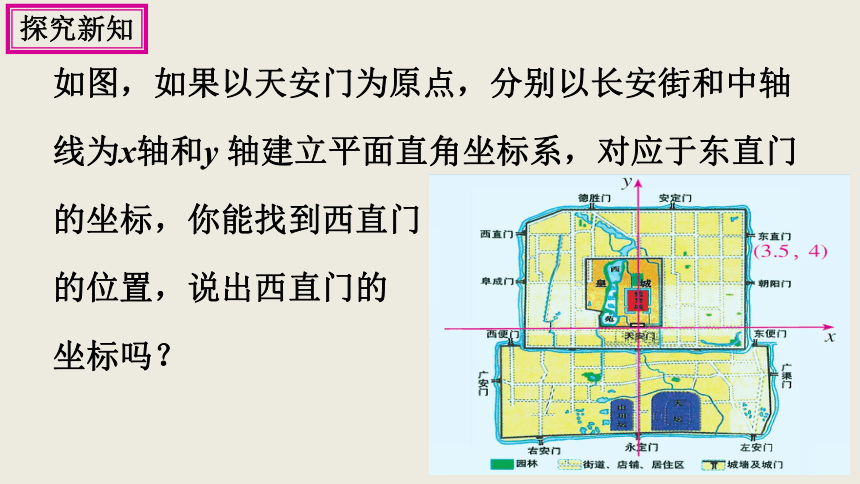
如图,如果以天安门为原点,分别以长安街和中轴
线为x轴和y 轴建立平面直角坐标系,对应于东直门
的坐标,你能找到西直门
的位置,说出西直门的
坐标吗?
探究新知
对于平面直角坐标系中任意一点,你能找出其关于
x 轴或y 轴对称的点的坐标吗?它们之间有什么规律?
探究新知
在平面直角坐标系中,画出下列已知点及其关于x 轴
对称的点,把它们的坐标填入表格中.
探究新知
x
y
1
1
O
A
B
C
D
E
A′
B′
C′
D′
E′
2,3
-1,-2
-6,5
4,0
关于x 轴对称的每对对称点的横坐标相等,纵坐标互为相反数.
观察下图中关于x 轴对称的每对对称点的坐标有怎
样的变化规律?
x
y
1
1
O
A
B
C
D
E
A′
B′
C′
D′
E′
探究归纳
探究新知
在平面直角坐标系中,画出下列已知点及其关于y 轴
对称的点,把它们的坐标填入表格中.
x
y
1
1
O
A
B
C
D
E
A〞
B〞
C〞
D〞
E〞
探究新知
-2 ,-3
1 ,2
6 ,-5
-4 ,0
关于y 轴对称的每对对称点的横坐标互为相反数,纵坐标相等.
观察下图中关于y 轴对称的每对对称点的坐标有怎
样的变化规律?
探究归纳
x
y
1
1
O
A
B
C
D
E
A〞
B〞
C〞
D〞
E〞
点(x,y)关于x 轴对称的点的坐标为(___,____);
点(x,y)关于y 轴对称的点的坐标为(___,____).
x -y
- x y
x
y
1
1
O
x
y
1
1
O
探究归纳
分别写出下列各点关于x 轴和y 轴对称的点的
坐标:(-2,6),(1,-2),(-1,3),
(-4,-2),(1,0) .
解:关于x 轴对称的点的坐标:(-2, -6),
(1,2),(-1, -3),(-4,2),(1,0) .
关于y 轴对称的点的坐标:(2,6),(-1,-2),(1,3),(4,-2),(-1,0) .
随堂练习
例:如图,四边形ABCD 的四个顶点的坐标分别为
A(-5,1),B(-2,1),
C(-2,5),D(-5,4),
分别画出与四边形ABCD 关
于x 轴和y 轴对称的图形.
x
y
1
1
O
A
B
C
D
探究新知
x
y
1
1
O
A
B
C
D
解:点(x,y)关于y 轴对称的点的坐标为(-x,y),因此四边形ABCD 的顶点A,B,C,
D 关于y 轴对称的点分别为:
A′( , ),
B′( , ),
C′( , ),
D′( , ),
2 5
5 1
2 1
5 4
A′
B′
C′
D′
探究新知
x
y
1
1
O
A
B
C
D
解:依次连接 A′B′ ,B′C′ ,C′D′,D′A′ ,
就可得到与四边形ABCD
关于y轴对称的四边形
A′B′C′D′ .
探究新知
A′
B′
C′
D′
请在图上画出四边形ABCD 关于x 轴对称的图形.
x
y
1
1
O
A
B
C
D
新知运用
解:点(x,y)关于x轴对称的点的坐标为(x,-y),因此四边形ABCD 的顶点A,B,C,D 关于x轴对称的点分别为:
A′( , ), B′( , ),
C′( , ), D′( , ).
x
y
1
1
O
A
B
C
D
5 -1
2 -1
2 -5
5 -4
A'
D'
C'
B'
探究运用
依次连接 A′B′ ,B′C′ ,C′D′,
D′A′ ,得到关于x轴对称的
四边形A′B′C′D′.
先求出已知图形中一些特殊点(多边形的顶点)的对称点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
步骤简述为:
(1)求特殊点的坐标;(2)描点;(3)连线.
归纳画一个图形关于x 轴或y 轴对称的图形的方法和步骤.
探究归纳
以正方形ABCD 的中心为原点建立平面直角坐标系.点A 的坐标为(1,1)、写出点B,C,D 的坐标.
A (1,1)
B
C
D
O
y
x
(1,-1)
(-1,-1)
(-1,1)
随堂练习
归纳总结
1、轴对称图形的画法;
2、在平面直角坐标系中,画出已知点及其关于坐标轴的对称点的画法;
3、在平面直角坐标系中,画一个图形关于x 轴或y 轴对称的图形的方法.
如何画线段AB关于直线l 的对称线段A′B′?
A
B
A’
作法:
1.过点A作直线l的垂线,垂足为点O,在垂线上截OA=O A′ ,点A′就是点A关于直线l的对称点;
2.类似地,作出点B关于直线l的对称点B′;
3.连接A′B′.
∴ 线段A ′ B ′即为所求.
A
B
巩固练习
O
如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
A.6cm B.4cm
C.3cm D.2cm
D
连接中考
1.作已知点关于某直线的对称点的第一步是( )
A.过已知点作一条直线与已知直线相交
B.过已知点作一条直线与已知直线垂直
C.过已知点作一条直线与已知直线平行
D.不确定
B
基础巩固题
课堂检测
2.如图,把一张长方形的纸按图那样折叠后,B,D两点落在B′,D′点处,若得∠AOB′=70°,则∠B′OG的度数为________.
55°
课堂检测
3.如图,把下列图形补成关于直线l的对称图形.
课堂检测
如图给出了一个图案的一半,虚线 l 是这个图案的对称轴.整个图案是个什么形状?请准确地画出它的另一半.
B
A
C
D
E
F
G
H
l
能力提升题
课堂检测
如图,画△ABC关于直线m的对称图形.
m
A
B
C
(A ′)
C ′
B ′
拓广探索题
课堂检测
画轴对称图形
作图原理
作图方法
对称轴是对称点连接的线段的垂直平分线
(1)找特殊点
(2)作垂线
(3)截取等长
(4)依次连线
课堂小结
13.2 画轴对称图形
一、什么是轴对称图形?什么叫两个图形成轴对称?
1、如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
2、对于两个图形,如果沿一条直线对折后,它们能完全重合,
那么这两个图形成轴对称,这条直线就是对称轴.
二、轴对称主要有哪些性质?
1、关于某条直线对称的两个图形是全等形;
2、如果两个图形关于某直线对称,那么对应点所连的线段被对称轴垂直平分;
3、成轴对称的两个图形的对应线段相等,对应角相等.
知识回顾
在一张半透明纸张的左边部分,画出左脚印,如何由此得到相应的右脚印?
探究新知
将这张纸对折后描图,打开对折的纸,就能得到相应的右脚印.
(1)画出的轴对称图形的形状、大小和原图形有什么
关系?
(2)画出的轴对称图形的点与原图形上的点有什么关系?
(3)对应点所连线段与对称轴有什么关系?
一个平面图形和与它成轴对称的另一个图形之间有什么关系?
答:由一个平面图形可以得到与它关于一条直线l 对称
的图形,这个图形与原图形的形状、大小完全相同;
答:新图形上的每一点都是原图形上的某一点关于直线 l 的对称点;
答:连接任意一对对应点的线段被对称轴垂直平分.
探究新知
(1)三角形关于直线l 的对称图形是什么形状?
(2)三角形的轴对称图形可以由哪几个点确定?
(3)如何作一个已知点关于直线l 的对称点?
A
B
C
l
A′
B′
C′
例1:如图,已知△ABC 和直线l,画出与△ABC
关于直线l 对称的图形.
探究新知
画法:(1)如图,过点A 画直线l 的垂线,垂足为点O,在垂线上截取OA′=OA,点A′就是点A 关于直线l 的对称点;
(2)同理,分别画点B,C 关于直线l 的对称点B′,C′;
(3)连接A′B′,B′C′,C′A′,所以△A′B′C′即为所求.
A
B
C
l
A′
B′
C′
例1:如图,已知△ABC 和直线l,画出与△ABC
关于直线l 对称的图形.
探究新知
可以通过折叠的方法来验证.
已知一个几何图形和一条直线,说一说画一个与该图形关于这条直线对称的图形的一般方法.
几何图形都可以看作由点组成.
对于某些图形,只要画出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
探究归纳
练习1:如图,把下列图形补成关于直线l 对称的图形.
l
l
l
随堂练习
练习2:用纸片剪一个三角形,分别沿它一边的中线、高、角平分线对折,看看哪些部分能够重合,哪些
部分不能重合.
沿角分线折叠
沿高折叠
沿中线折叠
随堂练习
如图,如果以天安门为原点,分别以长安街和中轴
线为x轴和y 轴建立平面直角坐标系,对应于东直门
的坐标,你能找到西直门
的位置,说出西直门的
坐标吗?
探究新知
对于平面直角坐标系中任意一点,你能找出其关于
x 轴或y 轴对称的点的坐标吗?它们之间有什么规律?
探究新知
在平面直角坐标系中,画出下列已知点及其关于x 轴
对称的点,把它们的坐标填入表格中.
探究新知
x
y
1
1
O
A
B
C
D
E
A′
B′
C′
D′
E′
2,3
-1,-2
-6,5
4,0
关于x 轴对称的每对对称点的横坐标相等,纵坐标互为相反数.
观察下图中关于x 轴对称的每对对称点的坐标有怎
样的变化规律?
x
y
1
1
O
A
B
C
D
E
A′
B′
C′
D′
E′
探究归纳
探究新知
在平面直角坐标系中,画出下列已知点及其关于y 轴
对称的点,把它们的坐标填入表格中.
x
y
1
1
O
A
B
C
D
E
A〞
B〞
C〞
D〞
E〞
探究新知
-2 ,-3
1 ,2
6 ,-5
-4 ,0
关于y 轴对称的每对对称点的横坐标互为相反数,纵坐标相等.
观察下图中关于y 轴对称的每对对称点的坐标有怎
样的变化规律?
探究归纳
x
y
1
1
O
A
B
C
D
E
A〞
B〞
C〞
D〞
E〞
点(x,y)关于x 轴对称的点的坐标为(___,____);
点(x,y)关于y 轴对称的点的坐标为(___,____).
x -y
- x y
x
y
1
1
O
x
y
1
1
O
探究归纳
分别写出下列各点关于x 轴和y 轴对称的点的
坐标:(-2,6),(1,-2),(-1,3),
(-4,-2),(1,0) .
解:关于x 轴对称的点的坐标:(-2, -6),
(1,2),(-1, -3),(-4,2),(1,0) .
关于y 轴对称的点的坐标:(2,6),(-1,-2),(1,3),(4,-2),(-1,0) .
随堂练习
例:如图,四边形ABCD 的四个顶点的坐标分别为
A(-5,1),B(-2,1),
C(-2,5),D(-5,4),
分别画出与四边形ABCD 关
于x 轴和y 轴对称的图形.
x
y
1
1
O
A
B
C
D
探究新知
x
y
1
1
O
A
B
C
D
解:点(x,y)关于y 轴对称的点的坐标为(-x,y),因此四边形ABCD 的顶点A,B,C,
D 关于y 轴对称的点分别为:
A′( , ),
B′( , ),
C′( , ),
D′( , ),
2 5
5 1
2 1
5 4
A′
B′
C′
D′
探究新知
x
y
1
1
O
A
B
C
D
解:依次连接 A′B′ ,B′C′ ,C′D′,D′A′ ,
就可得到与四边形ABCD
关于y轴对称的四边形
A′B′C′D′ .
探究新知
A′
B′
C′
D′
请在图上画出四边形ABCD 关于x 轴对称的图形.
x
y
1
1
O
A
B
C
D
新知运用
解:点(x,y)关于x轴对称的点的坐标为(x,-y),因此四边形ABCD 的顶点A,B,C,D 关于x轴对称的点分别为:
A′( , ), B′( , ),
C′( , ), D′( , ).
x
y
1
1
O
A
B
C
D
5 -1
2 -1
2 -5
5 -4
A'
D'
C'
B'
探究运用
依次连接 A′B′ ,B′C′ ,C′D′,
D′A′ ,得到关于x轴对称的
四边形A′B′C′D′.
先求出已知图形中一些特殊点(多边形的顶点)的对称点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
步骤简述为:
(1)求特殊点的坐标;(2)描点;(3)连线.
归纳画一个图形关于x 轴或y 轴对称的图形的方法和步骤.
探究归纳
以正方形ABCD 的中心为原点建立平面直角坐标系.点A 的坐标为(1,1)、写出点B,C,D 的坐标.
A (1,1)
B
C
D
O
y
x
(1,-1)
(-1,-1)
(-1,1)
随堂练习
归纳总结
1、轴对称图形的画法;
2、在平面直角坐标系中,画出已知点及其关于坐标轴的对称点的画法;
3、在平面直角坐标系中,画一个图形关于x 轴或y 轴对称的图形的方法.
如何画线段AB关于直线l 的对称线段A′B′?
A
B
A’
作法:
1.过点A作直线l的垂线,垂足为点O,在垂线上截OA=O A′ ,点A′就是点A关于直线l的对称点;
2.类似地,作出点B关于直线l的对称点B′;
3.连接A′B′.
∴ 线段A ′ B ′即为所求.
A
B
巩固练习
O
如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
A.6cm B.4cm
C.3cm D.2cm
D
连接中考
1.作已知点关于某直线的对称点的第一步是( )
A.过已知点作一条直线与已知直线相交
B.过已知点作一条直线与已知直线垂直
C.过已知点作一条直线与已知直线平行
D.不确定
B
基础巩固题
课堂检测
2.如图,把一张长方形的纸按图那样折叠后,B,D两点落在B′,D′点处,若得∠AOB′=70°,则∠B′OG的度数为________.
55°
课堂检测
3.如图,把下列图形补成关于直线l的对称图形.
课堂检测
如图给出了一个图案的一半,虚线 l 是这个图案的对称轴.整个图案是个什么形状?请准确地画出它的另一半.
B
A
C
D
E
F
G
H
l
能力提升题
课堂检测
如图,画△ABC关于直线m的对称图形.
m
A
B
C
(A ′)
C ′
B ′
拓广探索题
课堂检测
画轴对称图形
作图原理
作图方法
对称轴是对称点连接的线段的垂直平分线
(1)找特殊点
(2)作垂线
(3)截取等长
(4)依次连线
课堂小结
