2020-2021学年人教版数学八年级上册14.1.3积的乘方课件(15张)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册14.1.3积的乘方课件(15张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 00:00:00 | ||
图片预览





文档简介
人教版八年级数学上册第十五章
§15.1.3 积的乘方
认识新朋友,不忘老朋友!你还记得我吗?可不能喜新厌旧哦。
这里n为正整数,以下相同
回顾乘方的意义a =
n
a﹒a﹒a﹒ …﹒a﹒a
n个a
活动一:根据乘方的意义回答下列问题:
回顾复习 激疑启智
有奖竞答活动规则:
先举手“抢夺” 你感兴趣的人物(人物背后隐藏有题目),每答对一题者个人加一分。 注意:
题目不一定按导学案上的顺序出现。
(3)a 表示 ,即a = 。
5
5
我是犀利哥
(1) 表示 ,即 = ;
4
( -2 )
4
( -2 )
(2)( )表示 ,即( )= ;
1
8
6
1
8
6
活动二:计算,猜想:
(1)、22×32= ;(2×3) 2= ;
从而得到:(2×3)2 22×32
进而猜想:(ab)2与a2b2是否相等? (是/否)
( )6×(-2)6= ;﹝ ×(-2)﹞ 6= ;
从而得到:( )6×(-2)6 ﹝ ×(-2)﹞ 6
(2)、
八仙过海,各显其能。你可不能掉进海里淹死哟!记得要活着回来哟!
活动规则:各组长抽签选取任务,小组内合作讨论完成,然后选派代表发言或展示;答对者个人加一分,小组加一分。
36
36
=
1
1
=
1
2
1
2
1
2
1
2
(填“﹥”“﹤”或“=” )
(3)(ab)2 = ( ) ﹒ ( ) = ( ) ﹒ ( )= a ( ) b( ) ;
(4)(ab)3 = ( )﹒( )﹒( ) = ( ) ﹒ ( )= a ( ) b ( ) ;
…… …… ……
(5)(ab)n = ( )﹒( ) … ( ) =( )…( )= a( ) b( )
根据幂的
意义填空
根据乘法运算律
(交换律、结合律)填空
用文字语言叙述: ;
用符号语言表达: ;
积的乘方,等于各个因式乘方的积
ab
ab
aa
bb
2
2
ab
ab
ab
aaa
bbb
ab
ab
ab
aa…a
bb…b
3
3
n
n
(ab)n = a n· b n
活动二:计算,猜想:
积的乘方运算法则
有奖竞答活动规则:先举手“抢夺” 你有把握的题目,每答对一题者个人加一分。
当堂训练 及时巩固
(10)-p·(-2p)3= ;
(5)(-2)2(-3)2= ;
(6)(-2a2)3= ;
(7)(-2xy)4= ;
(8)(3a3)2= ;
(9)(2x2)3-(3x3)2= ;
活动规则:
各组长抽签选取两题,小组内合作讨论完成,然后选派代表发言或展示;答对者个人加一分,小组加一分。
(1) .
= ;
(3).
= ;
(2) .
= ;
(4).
= ;
a5b5
25a2b2
36
-27x3
16x4y4
x2y4
-x6
-8a6
9a6
8p4
1.计算:
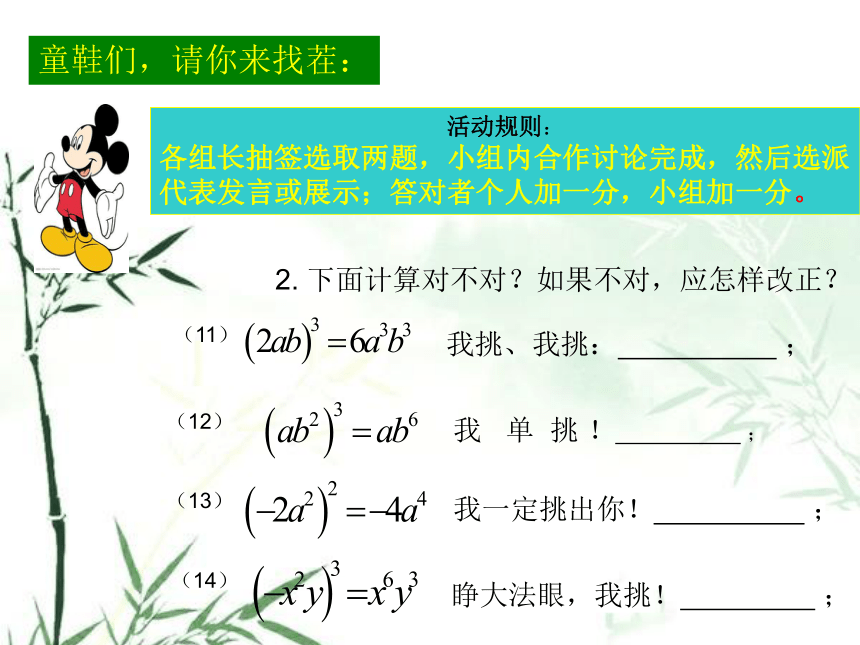
童鞋们,请你来找茬:
2. 下面计算对不对?如果不对,应怎样改正?
我挑、我挑: ;
我 单 挑 ! ;
我一定挑出你! ;
睁大法眼,我挑! ;
(11)
(13)
(14)
(12)
活动规则:
各组长抽签选取两题,小组内合作讨论完成,然后选派代表发言或展示;答对者个人加一分,小组加一分。
台风正猛,电闪雷鸣,风雨交加 ……
有个女的打来电话:“你好,我是社区的工作人员,我正在统计社区人口。请问你家是几口人?”
男答:“我家是一口人。”
女方:“十一口人?”
男说:“不是十一口人,而是一口人。”
女方:“二十一口?怎么又变成二十一口人了?”
男耐着性子说:“你听错了,其实一口人。”
女方:“七十一口人?怎么那么多呀?”
男终于爆发了,吼道:“就是一口人!”
女方:“九十一口人?天哪……”
男顿时崩溃……终于忍不住骂人了:“你个二百五!是一口人哪!”
女方:“二百五十一口人?不可能吧?”
只听到电话里传来“咚”的一声,再无声息 ……
哈哈哈……
可爱的女社区工作者,怎么就听不明白呢?
米老鼠赠言
欢笑之余,我们是否该认真反思一下女方的听讲状态呢?如果不集中注意力听别人讲话,是会闹出很多笑话来的。童鞋们,上课听讲可要专心哟。
情境剧扮演:需男女生各一名,分别扮演普通话不标准的男子和听讲马虎的女社区工作者。
难不倒你的,FIGHTING!!!
(-ab)
2
(1)
(2)
(x2y3)4
(-2a3y4)
(3)
3
恭喜你
直接加分!
(2)(-8)×(- )
2012
2011
游戏规则
各组指定一人“砸金蛋”选取题目,组内共同讨论完成,最后推举代表发言或展示;答对者加1~2分,小组加1分。
7、计算
你想挑战吗?你敢挑战吗?
8、计算:(-0.125)12×(-1 )7×(-8)13×(- )9.
活动规则
各组同时开始做,最后由各组期中成绩在50分以下的同学上台展示。展示合格后个人加3分,小组加1分。
想想看:怎么让50分以下的同学也学会?
解:原式
计算:
巩固练习
解析:∵2n+2n+2n+2n=2,
∴4?2n=2,∴2?2n=1,∴21+n=1,
∴1+n=0,∴n=–1.
A
连接中考
2.下列运算正确的是( )
A.(–a2)3=–a5 B.a3?a5=a15
C.(–a2b3)2=a4b6 D.3a2–2a2=1
C
(–a2)3= –a6;
a3?a5=a8;
3a2–2a2=a2
连接中考
2.下列运算正确的是( )
A. x?x2=x2 B. (xy)2=xy2
C. (x2)3=x6 D. x2+x2=x4
C
1.计算 (–x2y)2的结果是( )
A.x4y2 B.–x4y2
C.x2y2 D.–x2y2
A
课堂检测
基础巩固题
3. 计算:(1) 82016×0.1252015= ________;
(2) ________;
(3) (0.04)2013×[(–5)2013]2=________.
8
–3
1
(1)(ab2)3=ab6 ( )
×
×
×
(2) (3xy)3=9x3y3 ( )
×
(3) (–2a2)2=–4a4 ( )
(4) –(–ab2)2=a2b4 ( )
4. 判断:
课堂检测
(1) (ab)8 ; (2) (2m)3 ; (3) (–xy)5;
(4) (5ab2)3 ; (5) (2×102)2 ; (6) (–3×103)3.
5.计算:
解:(1)原式=a8b8;
(2)原式= 23 ·m3=8m3;
(3)原式=(–x)5 ·y5= –x5y5;
(4)原式=53 ·a3 ·(b2)3=125a3b6;
(5)原式=22 ×(102)2=4 ×104;
(6)原式=(–3)3 ×(103)3= –27 ×109= –2.7 ×1010.
课堂检测
(1) 2(x3)2·x3–(3x3)3+(5x)2·x7;
(2)(3xy2)2+(–4xy3) · (–xy) ;
(3)(–2x3)3·(x2)2.
解:原式=2x6·x3–27x9+25x2·x7
= 2x9–27x9+25x9 = 0;
解:原式=9x2y4 +4x2y4
=13x2y4;
解:原式= –8x9·x4 =–8x13.
计算:
能力提升题
课堂检测
如果(an?bm?b)3=a9b15,求m, n的值.
? (an)3?(bm)3?b3=a9b15,
? a 3n ?b 3m?b3=a9b15 ,
? a 3n ?b 3m+3=a9b15,
? 3n=9 ,3m+3=15.
?n=3,m=4.
解:∵(an?bm?b)3=a9b15,
拓广探索题
课堂检测
幂的运算性质
性质
am·an=am+n (am)n=amn (ab)n=anbn
( m、n都是正整数)
反向运用
am · an =am+n (am)n =amn an·bn = (ab)n
可使某些计算简捷
注意
运用积的乘方法则时要注意:
公式中的a、b代表任何代数式;每一个因式都要“乘方”;注意结果的符号、幂指数及其逆向运用(混合运算要注意运算顺序)
课堂检测
§15.1.3 积的乘方
认识新朋友,不忘老朋友!你还记得我吗?可不能喜新厌旧哦。
这里n为正整数,以下相同
回顾乘方的意义a =
n
a﹒a﹒a﹒ …﹒a﹒a
n个a
活动一:根据乘方的意义回答下列问题:
回顾复习 激疑启智
有奖竞答活动规则:
先举手“抢夺” 你感兴趣的人物(人物背后隐藏有题目),每答对一题者个人加一分。 注意:
题目不一定按导学案上的顺序出现。
(3)a 表示 ,即a = 。
5
5
我是犀利哥
(1) 表示 ,即 = ;
4
( -2 )
4
( -2 )
(2)( )表示 ,即( )= ;
1
8
6
1
8
6
活动二:计算,猜想:
(1)、22×32= ;(2×3) 2= ;
从而得到:(2×3)2 22×32
进而猜想:(ab)2与a2b2是否相等? (是/否)
( )6×(-2)6= ;﹝ ×(-2)﹞ 6= ;
从而得到:( )6×(-2)6 ﹝ ×(-2)﹞ 6
(2)、
八仙过海,各显其能。你可不能掉进海里淹死哟!记得要活着回来哟!
活动规则:各组长抽签选取任务,小组内合作讨论完成,然后选派代表发言或展示;答对者个人加一分,小组加一分。
36
36
=
1
1
=
1
2
1
2
1
2
1
2
(填“﹥”“﹤”或“=” )
(3)(ab)2 = ( ) ﹒ ( ) = ( ) ﹒ ( )= a ( ) b( ) ;
(4)(ab)3 = ( )﹒( )﹒( ) = ( ) ﹒ ( )= a ( ) b ( ) ;
…… …… ……
(5)(ab)n = ( )﹒( ) … ( ) =( )…( )= a( ) b( )
根据幂的
意义填空
根据乘法运算律
(交换律、结合律)填空
用文字语言叙述: ;
用符号语言表达: ;
积的乘方,等于各个因式乘方的积
ab
ab
aa
bb
2
2
ab
ab
ab
aaa
bbb
ab
ab
ab
aa…a
bb…b
3
3
n
n
(ab)n = a n· b n
活动二:计算,猜想:
积的乘方运算法则
有奖竞答活动规则:先举手“抢夺” 你有把握的题目,每答对一题者个人加一分。
当堂训练 及时巩固
(10)-p·(-2p)3= ;
(5)(-2)2(-3)2= ;
(6)(-2a2)3= ;
(7)(-2xy)4= ;
(8)(3a3)2= ;
(9)(2x2)3-(3x3)2= ;
活动规则:
各组长抽签选取两题,小组内合作讨论完成,然后选派代表发言或展示;答对者个人加一分,小组加一分。
(1) .
= ;
(3).
= ;
(2) .
= ;
(4).
= ;
a5b5
25a2b2
36
-27x3
16x4y4
x2y4
-x6
-8a6
9a6
8p4
1.计算:
童鞋们,请你来找茬:
2. 下面计算对不对?如果不对,应怎样改正?
我挑、我挑: ;
我 单 挑 ! ;
我一定挑出你! ;
睁大法眼,我挑! ;
(11)
(13)
(14)
(12)
活动规则:
各组长抽签选取两题,小组内合作讨论完成,然后选派代表发言或展示;答对者个人加一分,小组加一分。
台风正猛,电闪雷鸣,风雨交加 ……
有个女的打来电话:“你好,我是社区的工作人员,我正在统计社区人口。请问你家是几口人?”
男答:“我家是一口人。”
女方:“十一口人?”
男说:“不是十一口人,而是一口人。”
女方:“二十一口?怎么又变成二十一口人了?”
男耐着性子说:“你听错了,其实一口人。”
女方:“七十一口人?怎么那么多呀?”
男终于爆发了,吼道:“就是一口人!”
女方:“九十一口人?天哪……”
男顿时崩溃……终于忍不住骂人了:“你个二百五!是一口人哪!”
女方:“二百五十一口人?不可能吧?”
只听到电话里传来“咚”的一声,再无声息 ……
哈哈哈……
可爱的女社区工作者,怎么就听不明白呢?
米老鼠赠言
欢笑之余,我们是否该认真反思一下女方的听讲状态呢?如果不集中注意力听别人讲话,是会闹出很多笑话来的。童鞋们,上课听讲可要专心哟。
情境剧扮演:需男女生各一名,分别扮演普通话不标准的男子和听讲马虎的女社区工作者。
难不倒你的,FIGHTING!!!
(-ab)
2
(1)
(2)
(x2y3)4
(-2a3y4)
(3)
3
恭喜你
直接加分!
(2)(-8)×(- )
2012
2011
游戏规则
各组指定一人“砸金蛋”选取题目,组内共同讨论完成,最后推举代表发言或展示;答对者加1~2分,小组加1分。
7、计算
你想挑战吗?你敢挑战吗?
8、计算:(-0.125)12×(-1 )7×(-8)13×(- )9.
活动规则
各组同时开始做,最后由各组期中成绩在50分以下的同学上台展示。展示合格后个人加3分,小组加1分。
想想看:怎么让50分以下的同学也学会?
解:原式
计算:
巩固练习
解析:∵2n+2n+2n+2n=2,
∴4?2n=2,∴2?2n=1,∴21+n=1,
∴1+n=0,∴n=–1.
A
连接中考
2.下列运算正确的是( )
A.(–a2)3=–a5 B.a3?a5=a15
C.(–a2b3)2=a4b6 D.3a2–2a2=1
C
(–a2)3= –a6;
a3?a5=a8;
3a2–2a2=a2
连接中考
2.下列运算正确的是( )
A. x?x2=x2 B. (xy)2=xy2
C. (x2)3=x6 D. x2+x2=x4
C
1.计算 (–x2y)2的结果是( )
A.x4y2 B.–x4y2
C.x2y2 D.–x2y2
A
课堂检测
基础巩固题
3. 计算:(1) 82016×0.1252015= ________;
(2) ________;
(3) (0.04)2013×[(–5)2013]2=________.
8
–3
1
(1)(ab2)3=ab6 ( )
×
×
×
(2) (3xy)3=9x3y3 ( )
×
(3) (–2a2)2=–4a4 ( )
(4) –(–ab2)2=a2b4 ( )
4. 判断:
课堂检测
(1) (ab)8 ; (2) (2m)3 ; (3) (–xy)5;
(4) (5ab2)3 ; (5) (2×102)2 ; (6) (–3×103)3.
5.计算:
解:(1)原式=a8b8;
(2)原式= 23 ·m3=8m3;
(3)原式=(–x)5 ·y5= –x5y5;
(4)原式=53 ·a3 ·(b2)3=125a3b6;
(5)原式=22 ×(102)2=4 ×104;
(6)原式=(–3)3 ×(103)3= –27 ×109= –2.7 ×1010.
课堂检测
(1) 2(x3)2·x3–(3x3)3+(5x)2·x7;
(2)(3xy2)2+(–4xy3) · (–xy) ;
(3)(–2x3)3·(x2)2.
解:原式=2x6·x3–27x9+25x2·x7
= 2x9–27x9+25x9 = 0;
解:原式=9x2y4 +4x2y4
=13x2y4;
解:原式= –8x9·x4 =–8x13.
计算:
能力提升题
课堂检测
如果(an?bm?b)3=a9b15,求m, n的值.
? (an)3?(bm)3?b3=a9b15,
? a 3n ?b 3m?b3=a9b15 ,
? a 3n ?b 3m+3=a9b15,
? 3n=9 ,3m+3=15.
?n=3,m=4.
解:∵(an?bm?b)3=a9b15,
拓广探索题
课堂检测
幂的运算性质
性质
am·an=am+n (am)n=amn (ab)n=anbn
( m、n都是正整数)
反向运用
am · an =am+n (am)n =amn an·bn = (ab)n
可使某些计算简捷
注意
运用积的乘方法则时要注意:
公式中的a、b代表任何代数式;每一个因式都要“乘方”;注意结果的符号、幂指数及其逆向运用(混合运算要注意运算顺序)
课堂检测
