2020-2021学年人教版数学八年级上册14.2.1平方差公式课件(45张)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册14.2.1平方差公式课件(45张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 00:00:00 | ||
图片预览


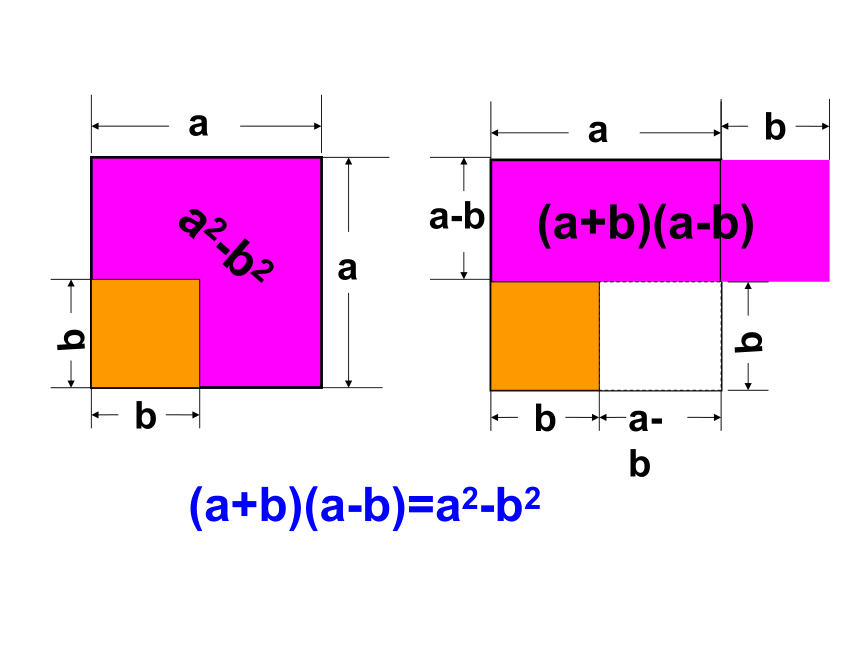
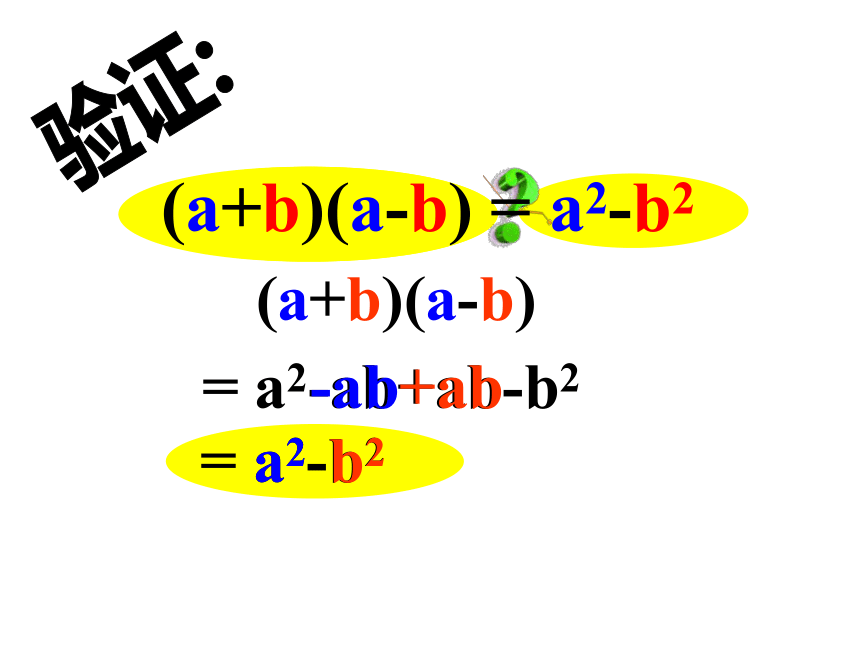





文档简介
14.2.1 平方差公式
计算下列多项式的积:
(x+1)(x-1) =
(m+2)(m-2) =
(2x+1)(2x-1) =
x2 - 1
m2 - 4
4x2 - 1
(3x)2 = ______
(- 4x)2 = ______
9x2
16x2
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
a-b
a-b
(a+b)(a-b) = a2-b2
(a+b)(a-b)
= a2-ab+ab-b2
-ab
+ab
= a2-b2
a2
b2
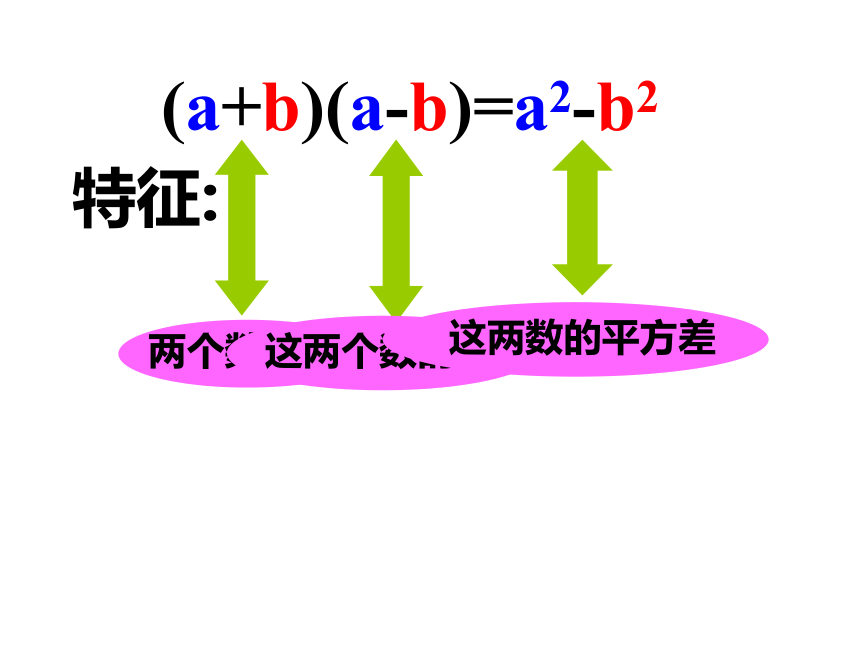
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,
等于这两个数的平方差.
§14.2.1 平方差公式
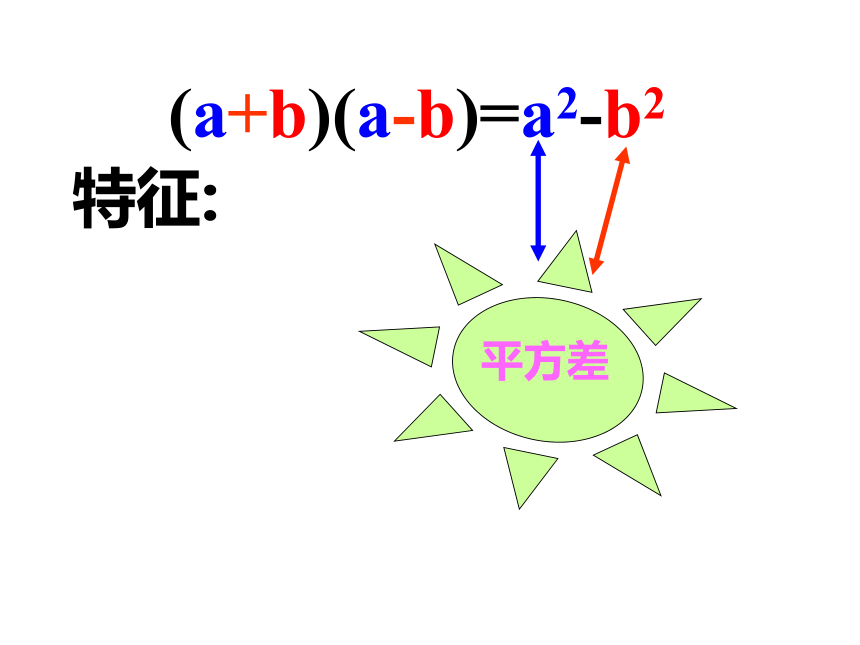
(a+b)(a-b)=a2-b2
特征:
两个数的和
这两个数的差
这两数的平方差
(a+b)(a-b)=a2-b2
特征:
两个二项式相乘
(a+b)(a-b)=a2-b2
特征:
符号相同
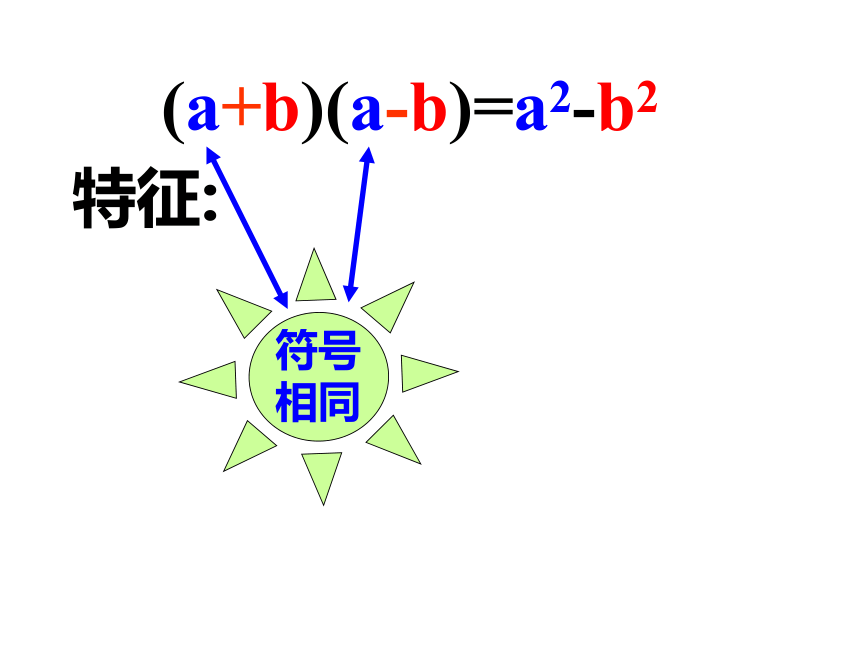
(a+b)(a-b)=a2-b2
特征:
符号
相反
(a+b)(a-b)=a2-b2
特征:
平方差
(a+b)(a-b)=a2-b2
特征:
(符号相同的项)2-(符号相反的项)2
(a+b)(a-b)=a2-b2
说明:
公式中的a,b可以表示具体的数(正数或负数),也可以表示一个单项式或一个多项式.
计算:
(x+1)(x-1) =
(m+2)(m-2) =
(2x+1)(2x-1) =
X2-1
m2-4
4x2-1
例1 运用平方差公式计算:
1、( 3x + 2 )( 3x – 2 ) ;
2、( b + 2a )( 2a – b );
3、( -x + 2y )( -x - 2y ).
分析:
⑴ (3x+2)(3x-2)
3x
3x
a
a
2
2
b
b
= a2 - b2
=
(3x)2
-
22
用公式关键是识别两数
符号相同的项 a
符号相反的项 b
(
)
(
)
+
-
解:
⑴ (3x+2)(3x-2)
=
(3x)2
3x
3x
-
2
2
22
= 9x2 - 4
⑵ (b+2a)(2a-b);
b
-b
+2a
2a
= (2a+b)(2a-b)
2a
2a
= (2a)2
= 4a2 – b2
b
b
-
b2
(3) (-x+2y)(-x-2y)
= (-x)2-(2y)2
= x2-4y2
计算下列各题,看谁做得又快又准?
(1)(x+1)(x-1)
(2)(m+2)(m-2)?
(3)(2x+1)(2x-1)
(4)(-3m-4)(-3m+4)
=x 2-1
=m 2-4
=4x 2-1
=9m 2-16
a2 - b2 =(a+b)(a-b)
逆向思维训练:
( n-m )( )=n2-m2
( -2x +__ ) ( ) =4x2-9y2
(-5+a)( ) =25-a?
计算:
(3-X)(3+X)
(2) (b+2a)(2a-b)
(3)(-X-2)(2-X)
ㄨ
下面各式的计算对不对?
如果不对,应当怎样改正?
(1) (x+2)(x-2) = x2 - 2
(2) (-3a-2)(3a-2) = 9a2 - 4
x2 - 4
ㄨ
4 - 9a2
运用平方 差公式计算:
(1) (a+3b)(a-3b) =
a2 - 9b2
(2) (3+2a)(-3+2a) =
4a2 - 9
(1) (a+b)(?a?b) ;
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y?2x).
(不能)
下列式子可用平方差公式计算吗? 为什么? 如果能够,怎样计算?
(第一个数不完全一样 )
(不能)
(不能)
(能)
?(a2 ?b2)=
?a2 + b2 ;
(不能)
下列各式中,能用平方差公式运算的是( )
A.(-a+b)(-a-b) B.(a-b)(b-a)
C.(2a-3b)(3a+2b) D.(a-b+c)(b-a-c)
2.下列各式相乘,不能用平方差公式计算的是( )
A.(x-2y)(2y+x) B.(-x+2y)(-x-2y)
C.(-2y-x)(x+2y) D.(-2b-5)(2b-5)
A
C
例2 计算 (1) a2 (a+b)(a?b)+ a2b2 (2)(2x-5)(2x+5)-2x(2x-3)
解:(1)原式= a2( a2-b2)+a2b2
=a4-a2b2+a2b2
=a4
(2)原式=(2 x )2 -25- (4 x 2-6 x )
=4 x 2 -25- 4 x 2+6 x
=6 x -25
例3 计算:
⑴ 102 ×98;
⑵ (y+2)(y-2)-(y-1)(y+5);
⑴ 102 ×98
动 脑筋!
谁是a?
谁是b?
102
= (100+2)
98
(100-2)
= 1002-22
= 10000-4
= 9996
⑵ (y+2)(y-2)-(y-1)(y+5)
动 脑筋!
y
y
y
y
2
2
= y2 - 22
1
5
- (y2+4y-5)
= y2-4-y2-4y+5
= -4y+1
运用平方差公式计算:
1、(p+q)(-q+p) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
5、 51 × 49 =
p2-q2
位置变化
y2-x2
符号变化
4a2-b2
系数变化
x4-y4
指数变化
2499
一拆为二
(a+b)(a-b)=a2-b2
1、 (2x-1)(2x+1)-2(x-2)(x+2)
2、(2n+3n)(2n-3n)
3、解方程:
3x(x+1)+(x+2)(x-2)=4(x2+8)
2x2+7
22n-32n
x=12
灵活运用平方差公式计算:
1、(3x+4)(3x-4) – (2x+3)(3x-2);
2、(x+y)(x-y)(x2+y2);
跳一跳:
( )
(x4+y4)
(x4+y4)
(x4+y4)
(2+1)(22+1)(24+1)(28+1) … (22n+1)
运用平方差公式计算:
王二小同学在计算(2+1)(22+1)(24+1)时,
将积式乘以(2-1)得:
解:原式 = (2-1)(2+1)(22+1)(24+1)
= (22-1)(22+1)(24+1)
= (24-1)(24+1)
= 28-1
你能根据上题计算:
(2+1)(22+1)(24+1)(28+1) … (22n+1)
的结果吗?
24n-1
(a+b-c)(a-b-c)能用平方差公式运算吗?若能结果是哪两数的平方差?
平方差公式
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,
等于这两个数的平方差.
如图1,在边长为a的正方形中挖掉一个边长为b的正方形(a>b ),把余下的部分剪成一个矩形(如图2).通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是( )
A. a2–b2 = (a+b) (a–b)
B. (a+b)2=a2+2ab+b2
C. (a–b)2=a2–2ab+b2
D. (a+2b)(a–b)=a2+ab–2b2
b
a
图1
b
a
图2
巩固练习
A
1. 化简(x–1)(x+1)的结果是 .
2. 某同学化简a(a+2b)–(a+b)(a–b)出现了错误,解答过程如下:原式=a2+2ab–(a2–b2) (第一步)
=a2+2ab–a2–b2(第二步)
=2ab–b2 (第三步)
(1)该同学解答过程从第 步开始出错,错误原因是 ;
(2)写出此题正确的解答过程.
原式=a2+2ab–(a2–b2)=a2+2ab–a2+b2=2ab+b2.
x2–1
二
去括号时没有变号
连接中考
1. 下列运算中,可用平方差公式计算的是( )
A.(x+y)(x+y) B.(–x+y)(x–y)
C.(–x–y)(y–x) D.(x+y)(–x–y)
C
2. 计算(2x+1)(2x–1)等于( )
A.4x2–1 B.2x2–1 C.4x–1 D.4x2+1
A
3. 两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是________.
10
基础巩固题
课堂检测
(1)(a+3b)(a– 3b);
=4a2–9;
=4x4–y2.
原式=(2a+3)(2a–3)
=a2–9b2 ;
=(2a)2–32
原式=(–2x2 )2–y2
原式=(a)2–(3b)2
(2)(3+2a)(–3+2a);
(3)(–2x2–y)(–2x2+y).
4. 利用平方差公式计算:
课堂检测
解:
解:
解:
5. 计算: 20152 – 2014×2016.
解:
20152 – 2014×2016
= 20152 – (2015–1)(2015+1)
= 20152
– (20152–12 )
= 20152
– 20152+12
=1
课堂检测
6. 利用平方差公式计算:
(1)(a–2)(a+2)(a2 + 4)
解:原式=(a2–4)(a2+4)
=a4–16.
(2) (x–y)(x+y)(x2+y2)(x4+y4).
解:原式=(x2–y2)(x2+y2)(x4+y4)
=(x4–y4)(x4+y4)
=x8–y8.
课堂检测
先化简,再求值:(x+1)(x–1) +x2(1–x) +x3,其中x=2.
解:原式=x2–1+x2–x3+x3
=2x2–1.
将x=2代入上式,
原式=2×22–1=7.
能力提升题
课堂检测
已知x≠1,计算:(1+x)(1–x)=1–x2,(1–x)(1+x+x2)=1–x3,
(1–x)(1+x+x2+x3)= 1–x4
(1)观察以上各式并猜想:(1–x)(1+x+x2+…+xn)=________;(n为正整数)
(2)根据你的猜想计算:
①(1–2)(1+2+22+23+24+25)=________;
②2+22+23+…+2n=________(n为正整数);
③(x–1)(x99+x98+x97+…+x2+x+1)=________;
1–xn+1
–63
2n+1–2
x100–1
拓广探索题
课堂检测
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差.
1.符号表示:(a+b)(a–b)=a2–b2
2.紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;对于不能直接应用公式的,可能要经过变形才可以应用.
课堂小结
计算下列多项式的积:
(x+1)(x-1) =
(m+2)(m-2) =
(2x+1)(2x-1) =
x2 - 1
m2 - 4
4x2 - 1
(3x)2 = ______
(- 4x)2 = ______
9x2
16x2
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
a-b
a-b
(a+b)(a-b) = a2-b2
(a+b)(a-b)
= a2-ab+ab-b2
-ab
+ab
= a2-b2
a2
b2
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,
等于这两个数的平方差.
§14.2.1 平方差公式
(a+b)(a-b)=a2-b2
特征:
两个数的和
这两个数的差
这两数的平方差
(a+b)(a-b)=a2-b2
特征:
两个二项式相乘
(a+b)(a-b)=a2-b2
特征:
符号相同
(a+b)(a-b)=a2-b2
特征:
符号
相反
(a+b)(a-b)=a2-b2
特征:
平方差
(a+b)(a-b)=a2-b2
特征:
(符号相同的项)2-(符号相反的项)2
(a+b)(a-b)=a2-b2
说明:
公式中的a,b可以表示具体的数(正数或负数),也可以表示一个单项式或一个多项式.
计算:
(x+1)(x-1) =
(m+2)(m-2) =
(2x+1)(2x-1) =
X2-1
m2-4
4x2-1
例1 运用平方差公式计算:
1、( 3x + 2 )( 3x – 2 ) ;
2、( b + 2a )( 2a – b );
3、( -x + 2y )( -x - 2y ).
分析:
⑴ (3x+2)(3x-2)
3x
3x
a
a
2
2
b
b
= a2 - b2
=
(3x)2
-
22
用公式关键是识别两数
符号相同的项 a
符号相反的项 b
(
)
(
)
+
-
解:
⑴ (3x+2)(3x-2)
=
(3x)2
3x
3x
-
2
2
22
= 9x2 - 4
⑵ (b+2a)(2a-b);
b
-b
+2a
2a
= (2a+b)(2a-b)
2a
2a
= (2a)2
= 4a2 – b2
b
b
-
b2
(3) (-x+2y)(-x-2y)
= (-x)2-(2y)2
= x2-4y2
计算下列各题,看谁做得又快又准?
(1)(x+1)(x-1)
(2)(m+2)(m-2)?
(3)(2x+1)(2x-1)
(4)(-3m-4)(-3m+4)
=x 2-1
=m 2-4
=4x 2-1
=9m 2-16
a2 - b2 =(a+b)(a-b)
逆向思维训练:
( n-m )( )=n2-m2
( -2x +__ ) ( ) =4x2-9y2
(-5+a)( ) =25-a?
计算:
(3-X)(3+X)
(2) (b+2a)(2a-b)
(3)(-X-2)(2-X)
ㄨ
下面各式的计算对不对?
如果不对,应当怎样改正?
(1) (x+2)(x-2) = x2 - 2
(2) (-3a-2)(3a-2) = 9a2 - 4
x2 - 4
ㄨ
4 - 9a2
运用平方 差公式计算:
(1) (a+3b)(a-3b) =
a2 - 9b2
(2) (3+2a)(-3+2a) =
4a2 - 9
(1) (a+b)(?a?b) ;
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y?2x).
(不能)
下列式子可用平方差公式计算吗? 为什么? 如果能够,怎样计算?
(第一个数不完全一样 )
(不能)
(不能)
(能)
?(a2 ?b2)=
?a2 + b2 ;
(不能)
下列各式中,能用平方差公式运算的是( )
A.(-a+b)(-a-b) B.(a-b)(b-a)
C.(2a-3b)(3a+2b) D.(a-b+c)(b-a-c)
2.下列各式相乘,不能用平方差公式计算的是( )
A.(x-2y)(2y+x) B.(-x+2y)(-x-2y)
C.(-2y-x)(x+2y) D.(-2b-5)(2b-5)
A
C
例2 计算 (1) a2 (a+b)(a?b)+ a2b2 (2)(2x-5)(2x+5)-2x(2x-3)
解:(1)原式= a2( a2-b2)+a2b2
=a4-a2b2+a2b2
=a4
(2)原式=(2 x )2 -25- (4 x 2-6 x )
=4 x 2 -25- 4 x 2+6 x
=6 x -25
例3 计算:
⑴ 102 ×98;
⑵ (y+2)(y-2)-(y-1)(y+5);
⑴ 102 ×98
动 脑筋!
谁是a?
谁是b?
102
= (100+2)
98
(100-2)
= 1002-22
= 10000-4
= 9996
⑵ (y+2)(y-2)-(y-1)(y+5)
动 脑筋!
y
y
y
y
2
2
= y2 - 22
1
5
- (y2+4y-5)
= y2-4-y2-4y+5
= -4y+1
运用平方差公式计算:
1、(p+q)(-q+p) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
5、 51 × 49 =
p2-q2
位置变化
y2-x2
符号变化
4a2-b2
系数变化
x4-y4
指数变化
2499
一拆为二
(a+b)(a-b)=a2-b2
1、 (2x-1)(2x+1)-2(x-2)(x+2)
2、(2n+3n)(2n-3n)
3、解方程:
3x(x+1)+(x+2)(x-2)=4(x2+8)
2x2+7
22n-32n
x=12
灵活运用平方差公式计算:
1、(3x+4)(3x-4) – (2x+3)(3x-2);
2、(x+y)(x-y)(x2+y2);
跳一跳:
( )
(x4+y4)
(x4+y4)
(x4+y4)
(2+1)(22+1)(24+1)(28+1) … (22n+1)
运用平方差公式计算:
王二小同学在计算(2+1)(22+1)(24+1)时,
将积式乘以(2-1)得:
解:原式 = (2-1)(2+1)(22+1)(24+1)
= (22-1)(22+1)(24+1)
= (24-1)(24+1)
= 28-1
你能根据上题计算:
(2+1)(22+1)(24+1)(28+1) … (22n+1)
的结果吗?
24n-1
(a+b-c)(a-b-c)能用平方差公式运算吗?若能结果是哪两数的平方差?
平方差公式
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,
等于这两个数的平方差.
如图1,在边长为a的正方形中挖掉一个边长为b的正方形(a>b ),把余下的部分剪成一个矩形(如图2).通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是( )
A. a2–b2 = (a+b) (a–b)
B. (a+b)2=a2+2ab+b2
C. (a–b)2=a2–2ab+b2
D. (a+2b)(a–b)=a2+ab–2b2
b
a
图1
b
a
图2
巩固练习
A
1. 化简(x–1)(x+1)的结果是 .
2. 某同学化简a(a+2b)–(a+b)(a–b)出现了错误,解答过程如下:原式=a2+2ab–(a2–b2) (第一步)
=a2+2ab–a2–b2(第二步)
=2ab–b2 (第三步)
(1)该同学解答过程从第 步开始出错,错误原因是 ;
(2)写出此题正确的解答过程.
原式=a2+2ab–(a2–b2)=a2+2ab–a2+b2=2ab+b2.
x2–1
二
去括号时没有变号
连接中考
1. 下列运算中,可用平方差公式计算的是( )
A.(x+y)(x+y) B.(–x+y)(x–y)
C.(–x–y)(y–x) D.(x+y)(–x–y)
C
2. 计算(2x+1)(2x–1)等于( )
A.4x2–1 B.2x2–1 C.4x–1 D.4x2+1
A
3. 两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是________.
10
基础巩固题
课堂检测
(1)(a+3b)(a– 3b);
=4a2–9;
=4x4–y2.
原式=(2a+3)(2a–3)
=a2–9b2 ;
=(2a)2–32
原式=(–2x2 )2–y2
原式=(a)2–(3b)2
(2)(3+2a)(–3+2a);
(3)(–2x2–y)(–2x2+y).
4. 利用平方差公式计算:
课堂检测
解:
解:
解:
5. 计算: 20152 – 2014×2016.
解:
20152 – 2014×2016
= 20152 – (2015–1)(2015+1)
= 20152
– (20152–12 )
= 20152
– 20152+12
=1
课堂检测
6. 利用平方差公式计算:
(1)(a–2)(a+2)(a2 + 4)
解:原式=(a2–4)(a2+4)
=a4–16.
(2) (x–y)(x+y)(x2+y2)(x4+y4).
解:原式=(x2–y2)(x2+y2)(x4+y4)
=(x4–y4)(x4+y4)
=x8–y8.
课堂检测
先化简,再求值:(x+1)(x–1) +x2(1–x) +x3,其中x=2.
解:原式=x2–1+x2–x3+x3
=2x2–1.
将x=2代入上式,
原式=2×22–1=7.
能力提升题
课堂检测
已知x≠1,计算:(1+x)(1–x)=1–x2,(1–x)(1+x+x2)=1–x3,
(1–x)(1+x+x2+x3)= 1–x4
(1)观察以上各式并猜想:(1–x)(1+x+x2+…+xn)=________;(n为正整数)
(2)根据你的猜想计算:
①(1–2)(1+2+22+23+24+25)=________;
②2+22+23+…+2n=________(n为正整数);
③(x–1)(x99+x98+x97+…+x2+x+1)=________;
1–xn+1
–63
2n+1–2
x100–1
拓广探索题
课堂检测
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差.
1.符号表示:(a+b)(a–b)=a2–b2
2.紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;对于不能直接应用公式的,可能要经过变形才可以应用.
课堂小结
