2020-2021学年人教版数学八年级上册15.1.1 从分数到分式课件(22张)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册15.1.1 从分数到分式课件(22张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 918.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 00:00:00 | ||
图片预览






文档简介
八年级 数学 人教版 上册
15.1 从分数到分式
二、学习目标
1.通过解决实际问题,能抽象出分式的概念。
2.了解分式的概念,能确定分式有无意义的条件,能确定分式的值为零的条件。(重难点)
3.体会类比的数学思想及方法。
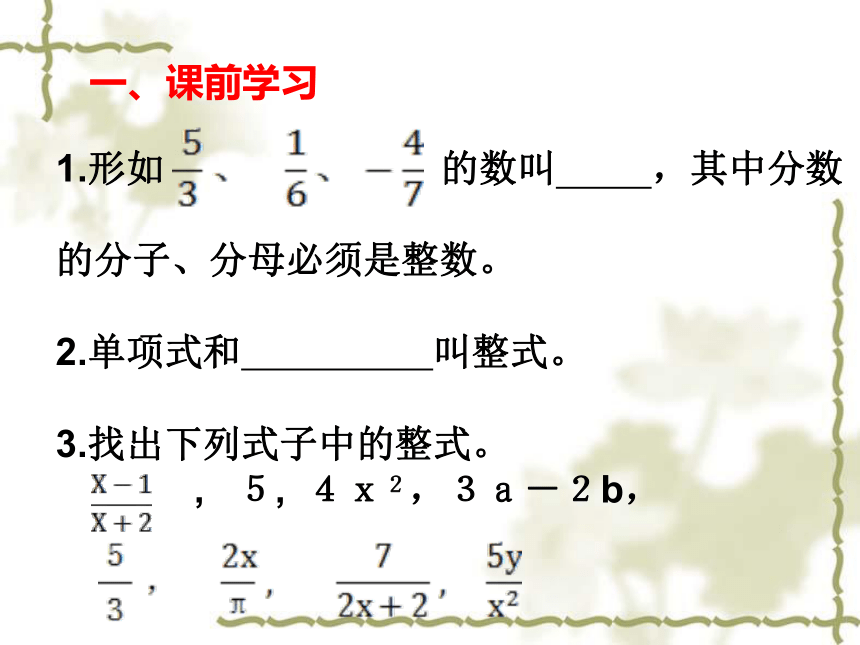
一、课前学习
1.形如 的数叫 ,其中分数
的分子、分母必须是整数。
2.单项式和 叫整式。
3.找出下列式子中的整式。
, 5, 4x2,3a-2b,
相同点:
不同点:
探究(一)分式的概念:
一般地,形如 的式子 ,其中A、B表示
两个整式,并且B中含有字母,这样的式子
叫分式。A叫做分子,B叫做分母。
当堂训练一
,
,
1.请写出三分式: 。
2.请找出下列式子中的分式。
X的取值
…
-3
-2
-1
0
1
2
3
…
…
有意义
…
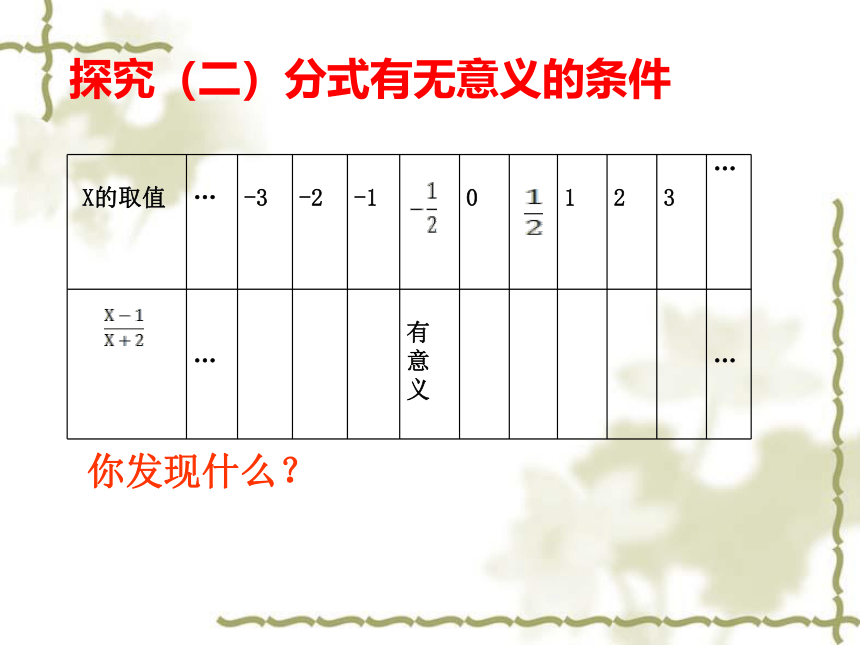
探究(二)分式有无意义的条件
你发现什么?
探究(二)分式有意义、无意义的条件
结论1.分式有意义的条件:分母不为零。
结论2.分式无意义的条件:分母为零。
探究(三)分式值为零的条件
X的取值
…
-3
-2
-1
0
1
2
3
…
分式
…
2
…
你发现什么?
探究(三)分式值为零的条件
1.分子等于零
2.分母不等于零
即:在分式 中,满足
则分式的值为零。
三、当堂训练
1.下列式子中的分母满足什么条件时分式有意义。
2.当分式中的字母取什么值时,分式的值为零
四、补读帮困
五、知者加速
六、总结建网
1.知识:
2.思想方法:
3.情感:
解析:由x2–1=0得
x2=1,
∴x=±1,
又∵x–1≠0即x≠1,
∴x= –1.
若分式: 的值为0,则( )
A.x=1 B.x= –1 C.x=±1 D.x≠1
B
巩固练习
解析:由分式的值为零的条件得x–3=0,且x+3≠0, 解得x=3.
D
A
连接中考
1.列式表示下列各量.
(1)某村有n个人,耕地40公顷,人均耕地面积为 公顷.
(2)△ABC的面积为S,BC边长为a,高AD长为 .
(3)一辆汽车行驶a千米用b小时,它的平均车速为 千米/小时;一列火车行驶a千米比这辆汽车少用1小时,它的平均车速为 千米/小时.
基础巩固题
课堂检测
2.下列各式中,哪些是分式?哪些是整式?
解:分式:
整式:
课堂检测
x≠–2
–3
课堂检测
当x取何值时,分式 有意义?x 取何值时,分式的值为0?
解: 时,分式有意义;
时,分式的值为0.
能力提升题
课堂检测
(1)y 的值为 0 ; (2)分式无意义 ;
(3)y的值为正数; (4)y的值为负数.
已知 ,x取何值时,满足:
拓广探究题
解:(1)当x=1时,y的值为0; (2)当x= 时,分式无意义;
(3)当 或 解得: <x<1.
(4)当 或 解得:x>1或x<
x–1>0
2–3x>0
x–1<0
2–3x<0
x–1>0
2–3x<0
x–1<0
2–3x>0
课堂检测
①如果A、B表示两个整式,且B中含有字母,那么式子 叫做分式.
②整式与分式的根本区别在于分母中含有字母.
分
式
定义
分式有意
义的条件
分式无意
义的条件
B≠0
B=0
B≠0,A=0
课堂小结
分式的值为0的条件
15.1 从分数到分式
二、学习目标
1.通过解决实际问题,能抽象出分式的概念。
2.了解分式的概念,能确定分式有无意义的条件,能确定分式的值为零的条件。(重难点)
3.体会类比的数学思想及方法。
一、课前学习
1.形如 的数叫 ,其中分数
的分子、分母必须是整数。
2.单项式和 叫整式。
3.找出下列式子中的整式。
, 5, 4x2,3a-2b,
相同点:
不同点:
探究(一)分式的概念:
一般地,形如 的式子 ,其中A、B表示
两个整式,并且B中含有字母,这样的式子
叫分式。A叫做分子,B叫做分母。
当堂训练一
,
,
1.请写出三分式: 。
2.请找出下列式子中的分式。
X的取值
…
-3
-2
-1
0
1
2
3
…
…
有意义
…
探究(二)分式有无意义的条件
你发现什么?
探究(二)分式有意义、无意义的条件
结论1.分式有意义的条件:分母不为零。
结论2.分式无意义的条件:分母为零。
探究(三)分式值为零的条件
X的取值
…
-3
-2
-1
0
1
2
3
…
分式
…
2
…
你发现什么?
探究(三)分式值为零的条件
1.分子等于零
2.分母不等于零
即:在分式 中,满足
则分式的值为零。
三、当堂训练
1.下列式子中的分母满足什么条件时分式有意义。
2.当分式中的字母取什么值时,分式的值为零
四、补读帮困
五、知者加速
六、总结建网
1.知识:
2.思想方法:
3.情感:
解析:由x2–1=0得
x2=1,
∴x=±1,
又∵x–1≠0即x≠1,
∴x= –1.
若分式: 的值为0,则( )
A.x=1 B.x= –1 C.x=±1 D.x≠1
B
巩固练习
解析:由分式的值为零的条件得x–3=0,且x+3≠0, 解得x=3.
D
A
连接中考
1.列式表示下列各量.
(1)某村有n个人,耕地40公顷,人均耕地面积为 公顷.
(2)△ABC的面积为S,BC边长为a,高AD长为 .
(3)一辆汽车行驶a千米用b小时,它的平均车速为 千米/小时;一列火车行驶a千米比这辆汽车少用1小时,它的平均车速为 千米/小时.
基础巩固题
课堂检测
2.下列各式中,哪些是分式?哪些是整式?
解:分式:
整式:
课堂检测
x≠–2
–3
课堂检测
当x取何值时,分式 有意义?x 取何值时,分式的值为0?
解: 时,分式有意义;
时,分式的值为0.
能力提升题
课堂检测
(1)y 的值为 0 ; (2)分式无意义 ;
(3)y的值为正数; (4)y的值为负数.
已知 ,x取何值时,满足:
拓广探究题
解:(1)当x=1时,y的值为0; (2)当x= 时,分式无意义;
(3)当 或 解得: <x<1.
(4)当 或 解得:x>1或x<
x–1>0
2–3x>0
x–1<0
2–3x<0
x–1>0
2–3x<0
x–1<0
2–3x>0
课堂检测
①如果A、B表示两个整式,且B中含有字母,那么式子 叫做分式.
②整式与分式的根本区别在于分母中含有字母.
分
式
定义
分式有意
义的条件
分式无意
义的条件
B≠0
B=0
B≠0,A=0
课堂小结
分式的值为0的条件
