2020-2021学年人教版数学八年级上册15.2.1分式的乘除课件(24张)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册15.2.1分式的乘除课件(24张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 777.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 00:00:00 | ||
图片预览








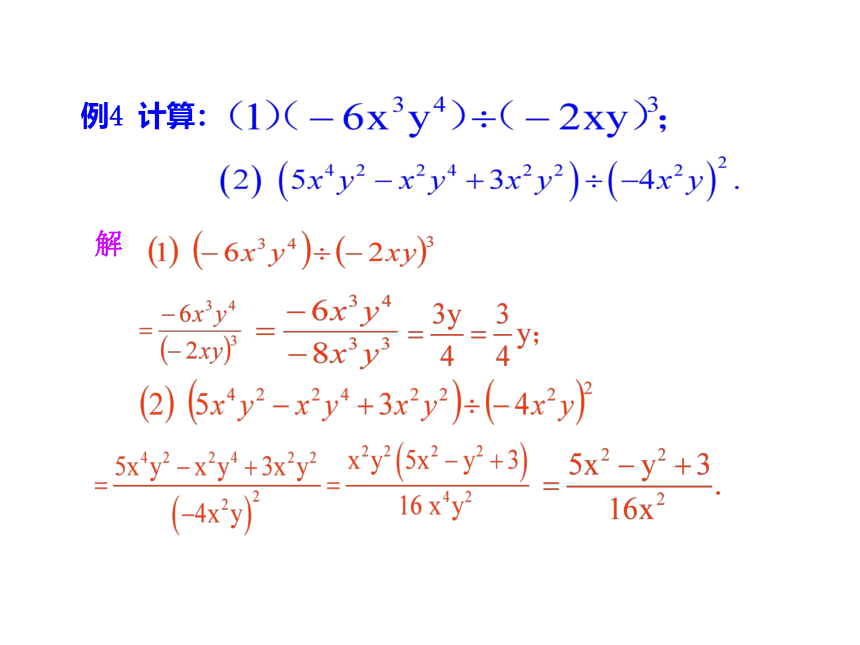
文档简介
15.2.1分式的乘除
学习目标:
能应用分式的乘除法法则进行乘除混合运算。
学习重点:
分式乘除法法则及其应用
学习难点:
分式乘除法法则及其应用
【分数的乘除法法则 】
情境引入:我们已经学过分数的乘除法法则
两个分数相乘, 把分子相乘的积作为积的分子,把分母相乘的积作为积的分母.
两个分数相除, 把除式的分子分母颠倒位置后,再与被除式相乘.
分式乘法法则:分式乘分式,用分子的积作为积
的分子,分母的积作为积的分母.
分式除法法则:分式除以分式,把除式的分子、
分母颠倒位置后,与被除式相乘.
类比分数的乘除法法则,我们能不能得出分式的乘除法法则呢?
式子表示
式子表示
字母a,b,c,d都是整式,但b,c,d不为零
例1 计算:
解(1)
(2)
1.计算:
解:原式
例2 计算:
2.计算:
解:原式
例2 计算:
例3
计算
解:
归纳 乘除混合运算可以统一为乘法运算
例4 计算:
解
1.计算 等于( )
A. B. C. D.
【解析】选C.
2. 化简 的结果是( )
A. B.a C.a-1 D.
【解析】选B.
3.计算: =__________________.
【解析】
答案:
4.计算:
5.先化简
然后从-1,1,2中选取一个数作为x的值代入求值.
【解析】(1)原式=
因为分母x-1≠0,x+1≠0,
所以x≠1且x≠-1,
所以取x=2,
所以
1.理解并掌握分式乘除法的法则,会进行分式乘除运算.
2.熟练地进行分式乘、除、乘方的混合运算.
3.能解决一些与分式乘除法有关的实际问题.
第一步,把线段AB三等分,以中间的一段为边作等边三角形,然后去掉这一段,就得到由4条长度相等的线段组成的折线,总长度为
第二步,把上述折线中每一条线段重复第一步的做法,便得到由长度相等的线段组成的折线,总长度为
取一条长度为1个单位的线段AB,如图
巩固练习
按照上述方法一步一步地继续进行下去,在图中画出了第一步至第五步所得到的折线的形状.
你觉得第五步得到的折线漂亮吗?
巩固练习
对于任意一个正整数n,第n步得到的折线的总长度是多少?
你能推算出第五步得到的折线的总长度吗?
巩固练习
1.老师设计了接力游戏,用合作的方式完成分式化简,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图所示:
接力中,自己负责的一步出现错误的是( )
A.只有乙 B.甲和丁 C.乙和丙 D.乙和丁
D
A
连接中考
基础巩固题
B
课堂检测
2.计算: =__________________.
课堂检测
解:原式
解:原式
3.计算:
(1)
(2)
先化简 然后从–1,1,2中选取一个数作为x的值代入求值.
解:(1)原式=
因为分母x–1≠0,x+1≠0,
所以x≠1且x≠ – 1,
所以取x=2,所以
能力提升题
课堂检测
一条船往返于水路相距100km的A,B两地之间,已知水流的速度是每小时2km,船在静水中的速度是每小时xkm(x>2),那么船在往返一次过程中,顺流航行的时间与逆流航行的时间比是______.
拓广探索题
课堂检测
分式的乘除法法则
课堂小结
①若分子分母都是单项式,把分子分母分别相乘,约去公因式,最后化为最简分式或整式;
②若分子分母有多项式,先把多项式分解因式,看能约分的先约分,然后相乘;
③分式与分式相除时,按照法则先转化为乘法,再运算.
注意事项:
学习目标:
能应用分式的乘除法法则进行乘除混合运算。
学习重点:
分式乘除法法则及其应用
学习难点:
分式乘除法法则及其应用
【分数的乘除法法则 】
情境引入:我们已经学过分数的乘除法法则
两个分数相乘, 把分子相乘的积作为积的分子,把分母相乘的积作为积的分母.
两个分数相除, 把除式的分子分母颠倒位置后,再与被除式相乘.
分式乘法法则:分式乘分式,用分子的积作为积
的分子,分母的积作为积的分母.
分式除法法则:分式除以分式,把除式的分子、
分母颠倒位置后,与被除式相乘.
类比分数的乘除法法则,我们能不能得出分式的乘除法法则呢?
式子表示
式子表示
字母a,b,c,d都是整式,但b,c,d不为零
例1 计算:
解(1)
(2)
1.计算:
解:原式
例2 计算:
2.计算:
解:原式
例2 计算:
例3
计算
解:
归纳 乘除混合运算可以统一为乘法运算
例4 计算:
解
1.计算 等于( )
A. B. C. D.
【解析】选C.
2. 化简 的结果是( )
A. B.a C.a-1 D.
【解析】选B.
3.计算: =__________________.
【解析】
答案:
4.计算:
5.先化简
然后从-1,1,2中选取一个数作为x的值代入求值.
【解析】(1)原式=
因为分母x-1≠0,x+1≠0,
所以x≠1且x≠-1,
所以取x=2,
所以
1.理解并掌握分式乘除法的法则,会进行分式乘除运算.
2.熟练地进行分式乘、除、乘方的混合运算.
3.能解决一些与分式乘除法有关的实际问题.
第一步,把线段AB三等分,以中间的一段为边作等边三角形,然后去掉这一段,就得到由4条长度相等的线段组成的折线,总长度为
第二步,把上述折线中每一条线段重复第一步的做法,便得到由长度相等的线段组成的折线,总长度为
取一条长度为1个单位的线段AB,如图
巩固练习
按照上述方法一步一步地继续进行下去,在图中画出了第一步至第五步所得到的折线的形状.
你觉得第五步得到的折线漂亮吗?
巩固练习
对于任意一个正整数n,第n步得到的折线的总长度是多少?
你能推算出第五步得到的折线的总长度吗?
巩固练习
1.老师设计了接力游戏,用合作的方式完成分式化简,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图所示:
接力中,自己负责的一步出现错误的是( )
A.只有乙 B.甲和丁 C.乙和丙 D.乙和丁
D
A
连接中考
基础巩固题
B
课堂检测
2.计算: =__________________.
课堂检测
解:原式
解:原式
3.计算:
(1)
(2)
先化简 然后从–1,1,2中选取一个数作为x的值代入求值.
解:(1)原式=
因为分母x–1≠0,x+1≠0,
所以x≠1且x≠ – 1,
所以取x=2,所以
能力提升题
课堂检测
一条船往返于水路相距100km的A,B两地之间,已知水流的速度是每小时2km,船在静水中的速度是每小时xkm(x>2),那么船在往返一次过程中,顺流航行的时间与逆流航行的时间比是______.
拓广探索题
课堂检测
分式的乘除法法则
课堂小结
①若分子分母都是单项式,把分子分母分别相乘,约去公因式,最后化为最简分式或整式;
②若分子分母有多项式,先把多项式分解因式,看能约分的先约分,然后相乘;
③分式与分式相除时,按照法则先转化为乘法,再运算.
注意事项:
