第3 章勾股定理 单元小结与思考---课时作业 2021-2022学年苏科版数学八年级上册(word版含答案)
文档属性
| 名称 | 第3 章勾股定理 单元小结与思考---课时作业 2021-2022学年苏科版数学八年级上册(word版含答案) | 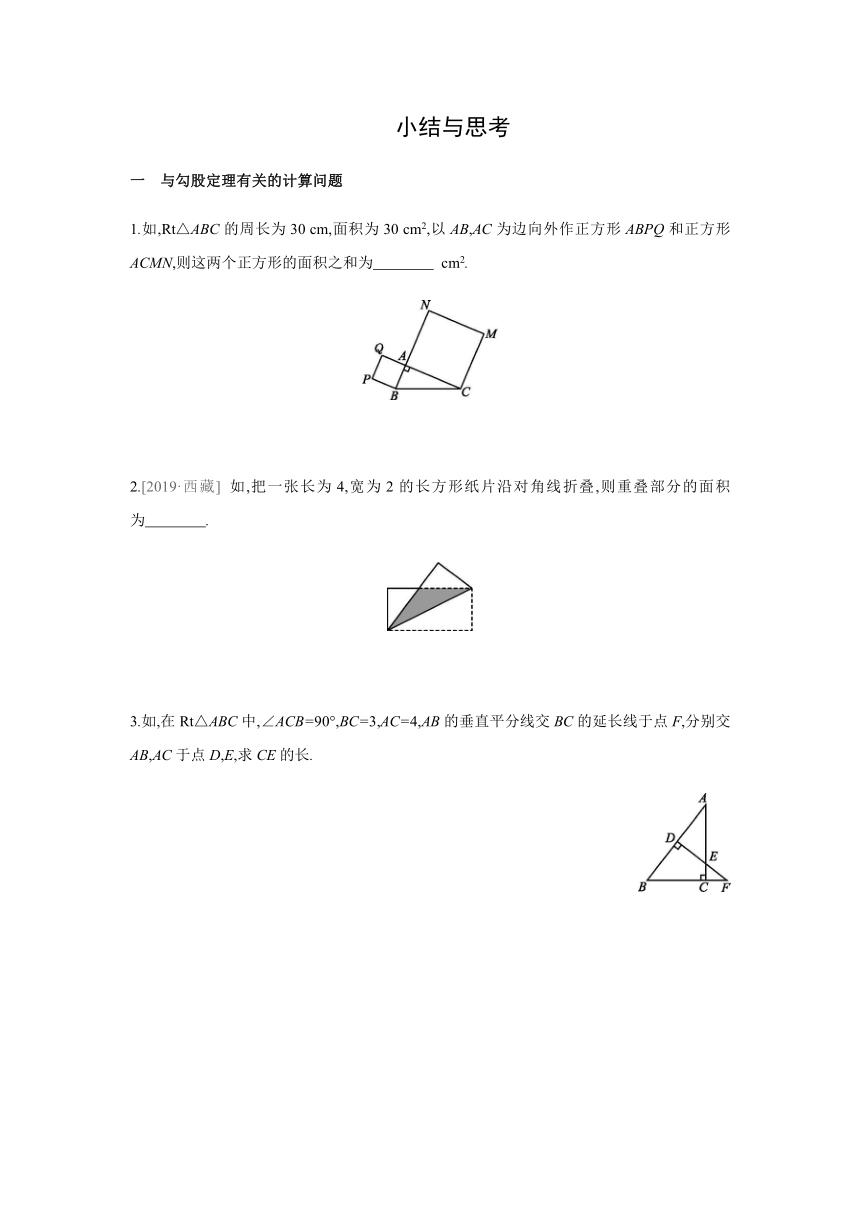 | |
| 格式 | docx | ||
| 文件大小 | 164.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 06:25:52 | ||
图片预览





文档简介
小结与思考
一 与勾股定理有关的计算问题
1.如,Rt△ABC的周长为30 cm,面积为30 cm2,以AB,AC为边向外作正方形ABPQ和正方形ACMN,则这两个正方形的面积之和为 cm2.?
2.[2019·西藏] 如,把一张长为4,宽为2的长方形纸片沿对角线折叠,则重叠部分的面积为 .?
3.如,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线交BC的延长线于点F,分别交AB,AC于点D,E,求CE的长.
4.如,在△ABC中,AB=AC=5,BC=8,CD是AB边上的高,求线段AD的长.
二 勾股定理的验证
5.[2020·宁夏] 2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的“勾股圆方图”,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如①).已知大正方形的面积是15,小正方形的面积是3,直角三角形的较短直角边长为a,较长直角边长为b.如果将四个全等的直角三角形按如图②的形式摆放,那么图②中最大的正方形的面积为 .?
6.勾股定理的证法多样,其中“面积法”是常用方法,小明发现:当四个全等的直角三角形如摆放时,可以用“面积法”来证明勾股定理.(请你写出证明过程)
三 勾股定理的逆定理
7.下列长度的三条线段不能组成直角三角形的是 ( )
A.3,4,5 B.6,8,10
C.5,12,13 D.5,12,15
8.[2019·南京建邺区期末] 如,在△ABC中,∠ABC=∠ACB,AC=3,D是CA延长线上一点,AD=5,BD=4.求证:AB⊥BD.
四 勾股定理在实际生活中的应用
9.[2020·南京溧水区期中改编] 小明拿着一根竹竿进一个宽3米的大门,他竖起来拿时,结果竹竿比大门高32米;当他把竹竿斜着拿时,两端恰好顶着大门的对角,则这根竹竿的长为
米.?
10.[2019·南京] 无盖圆柱形杯子的展开图如所示.将一根长为20 cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 cm.?
11.[2020·宜兴期中] 如,OA⊥OB,OA=45海里,OB=15海里,我国钓鱼岛位于点O,我国渔政船在点B处发现有一不明国籍的渔船,自点A出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国渔政船立即从点B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.
(1)请用直尺和圆规作出点C处的位置;
(2)求我国渔政船行驶的航程BC的长.
12.如,在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点H(点A,H,B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,BH=1.8千米.
(1)CH与AB是否垂直?请通过计算加以说明;
(2)求原来的路AC的长.
五 数学活动
13.某学校综合实践活动小组研制了一套信号发射、接收系统,为了对系统性能进行测试,小明自A处出发,沿西南方向的笔直公路行进,并发射信号.小华同时从A处出发,沿东南方向的笔直公路行进,并接收信号.若小明的步行速度为39米/分,小华的步行速度为52米/分,恰好在出发后30分钟时信号开始不清晰,此时他们分别位于B,C处(如).
(1)以信号清晰为界限,请你求出信号的传送半径;
(2)通过计算,寻找题中数据与勾股数3,4,5的联系,并从中寻找解决问题的简便算法.
教师详解详析
1.169 [解析] ∵Rt△ABC的周长为30 cm,面积为30 cm2,∴AC+AB=30-BC,AC·AB=60.
∴(AC+AB)2=AC2+AB2+2AC·AB=BC2+120=(30-BC)2,解得BC=13.
∴两个正方形的面积之和为AC2+AB2=BC2=169 cm2.
2.2.5
3.解:如图,连接BE.
∵DE是AB的垂直平分线,∴AE=BE.
在Rt△EBC中,BE2=CE2+BC2,
即(4-CE)2=CE2+32,
解得CE=78.
4.解:设AD=x,则BD=5+x.
∵CD⊥AB,∴∠D=90°,
在Rt△CBD与Rt△ACD中,
CD2=BC2-BD2,CD2=AC2-AD2,
∴BC2-BD2=AC2-AD2,
∴82-(5+x)2=52-x2,
解得x=75.
∴AD=75.
5.27 [解析] 由题意可知,
在图①中,a2+b2=15,(b-a)2=3,
在图②中,大正方形的面积为(a+b)2.
∵(b-a)2=3,即a2-2ab+b2=3,
∴15-2ab=3,∴2ab=12,
∴(a+b)2=a2+2ab+b2=15+12=27.
故答案为27.
6.证明:如图.∵S五边形ABDEF=S梯形ABCF+S梯形CDEF=S正方形AGEF+2S直角三角形,
即12(b+a+b)b+12(a+a+b)a=c2+2×12ab,
12ab+b2+12ab+a2=c2+ab,
∴a2+b2=c2.
7.D [解析] 欲证明是不是直角三角形,这里给出三边的长,只要验证两较小边的平方和是否等于最长边的平方即可.
8.证明:∵∠ABC=∠ACB,AC=3,
∴AB=AC=3.
∵AD=5,BD=4,
∴AB2+BD2=25,AD2=25,
∴AB2+BD2=AD2,
∴△ABD是直角三角形,且∠ABD=90°,
即AB⊥BD.
9.154 [解析] 设这根竹竿的长为x米.
由题意,得x-322+32=x2,解得x=154.
10.5
11.解:(1)如图,连线AB,作AB的垂直平分线与AO交于点C,则点C即为所求.
(2)设BC为x海里,则CA=x海里,
∴OC=(45-x)海里.
∵OA⊥OB,∴∠O=90°,
∴在Rt△OBC中,OB2+OC2=BC2,
即152+(45-x)2=x2,解得x=25.
答:我国渔政船行驶的航程BC的长为25海里.
12.解:(1)CH⊥AB.
说明如下:在△CHB中,
∵CH2+BH2=2.42+1.82=9,
BC2=9,
∴CH2+BH2=BC2.
∴△CHB为直角三角形,且∠BHC=90°.
∴CH⊥AB.
(2)设AC=x千米.
在Rt△ACH中,由已知得AH=(x-1.8)千米,CH=2.4千米.
由勾股定理,得AC2=AH2+CH2,
∴x2=(x-1.8)2+2.42,
解得x=2.5.
答:原来的路AC的长为2.5千米.
13.解:(1)利用勾股定理求出信号的传送半径为1950米.
(2)小明所走的路程为39×30=3×13×30=1170(米),小华所走的路程为52×30=4×13×30=1560(米).
因为勾股数3,4,5的倍数仍能构成一组勾股数,故所求半径为5×13×30=1950(米).
一 与勾股定理有关的计算问题
1.如,Rt△ABC的周长为30 cm,面积为30 cm2,以AB,AC为边向外作正方形ABPQ和正方形ACMN,则这两个正方形的面积之和为 cm2.?
2.[2019·西藏] 如,把一张长为4,宽为2的长方形纸片沿对角线折叠,则重叠部分的面积为 .?
3.如,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线交BC的延长线于点F,分别交AB,AC于点D,E,求CE的长.
4.如,在△ABC中,AB=AC=5,BC=8,CD是AB边上的高,求线段AD的长.
二 勾股定理的验证
5.[2020·宁夏] 2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的“勾股圆方图”,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如①).已知大正方形的面积是15,小正方形的面积是3,直角三角形的较短直角边长为a,较长直角边长为b.如果将四个全等的直角三角形按如图②的形式摆放,那么图②中最大的正方形的面积为 .?
6.勾股定理的证法多样,其中“面积法”是常用方法,小明发现:当四个全等的直角三角形如摆放时,可以用“面积法”来证明勾股定理.(请你写出证明过程)
三 勾股定理的逆定理
7.下列长度的三条线段不能组成直角三角形的是 ( )
A.3,4,5 B.6,8,10
C.5,12,13 D.5,12,15
8.[2019·南京建邺区期末] 如,在△ABC中,∠ABC=∠ACB,AC=3,D是CA延长线上一点,AD=5,BD=4.求证:AB⊥BD.
四 勾股定理在实际生活中的应用
9.[2020·南京溧水区期中改编] 小明拿着一根竹竿进一个宽3米的大门,他竖起来拿时,结果竹竿比大门高32米;当他把竹竿斜着拿时,两端恰好顶着大门的对角,则这根竹竿的长为
米.?
10.[2019·南京] 无盖圆柱形杯子的展开图如所示.将一根长为20 cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 cm.?
11.[2020·宜兴期中] 如,OA⊥OB,OA=45海里,OB=15海里,我国钓鱼岛位于点O,我国渔政船在点B处发现有一不明国籍的渔船,自点A出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国渔政船立即从点B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.
(1)请用直尺和圆规作出点C处的位置;
(2)求我国渔政船行驶的航程BC的长.
12.如,在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点H(点A,H,B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,BH=1.8千米.
(1)CH与AB是否垂直?请通过计算加以说明;
(2)求原来的路AC的长.
五 数学活动
13.某学校综合实践活动小组研制了一套信号发射、接收系统,为了对系统性能进行测试,小明自A处出发,沿西南方向的笔直公路行进,并发射信号.小华同时从A处出发,沿东南方向的笔直公路行进,并接收信号.若小明的步行速度为39米/分,小华的步行速度为52米/分,恰好在出发后30分钟时信号开始不清晰,此时他们分别位于B,C处(如).
(1)以信号清晰为界限,请你求出信号的传送半径;
(2)通过计算,寻找题中数据与勾股数3,4,5的联系,并从中寻找解决问题的简便算法.
教师详解详析
1.169 [解析] ∵Rt△ABC的周长为30 cm,面积为30 cm2,∴AC+AB=30-BC,AC·AB=60.
∴(AC+AB)2=AC2+AB2+2AC·AB=BC2+120=(30-BC)2,解得BC=13.
∴两个正方形的面积之和为AC2+AB2=BC2=169 cm2.
2.2.5
3.解:如图,连接BE.
∵DE是AB的垂直平分线,∴AE=BE.
在Rt△EBC中,BE2=CE2+BC2,
即(4-CE)2=CE2+32,
解得CE=78.
4.解:设AD=x,则BD=5+x.
∵CD⊥AB,∴∠D=90°,
在Rt△CBD与Rt△ACD中,
CD2=BC2-BD2,CD2=AC2-AD2,
∴BC2-BD2=AC2-AD2,
∴82-(5+x)2=52-x2,
解得x=75.
∴AD=75.
5.27 [解析] 由题意可知,
在图①中,a2+b2=15,(b-a)2=3,
在图②中,大正方形的面积为(a+b)2.
∵(b-a)2=3,即a2-2ab+b2=3,
∴15-2ab=3,∴2ab=12,
∴(a+b)2=a2+2ab+b2=15+12=27.
故答案为27.
6.证明:如图.∵S五边形ABDEF=S梯形ABCF+S梯形CDEF=S正方形AGEF+2S直角三角形,
即12(b+a+b)b+12(a+a+b)a=c2+2×12ab,
12ab+b2+12ab+a2=c2+ab,
∴a2+b2=c2.
7.D [解析] 欲证明是不是直角三角形,这里给出三边的长,只要验证两较小边的平方和是否等于最长边的平方即可.
8.证明:∵∠ABC=∠ACB,AC=3,
∴AB=AC=3.
∵AD=5,BD=4,
∴AB2+BD2=25,AD2=25,
∴AB2+BD2=AD2,
∴△ABD是直角三角形,且∠ABD=90°,
即AB⊥BD.
9.154 [解析] 设这根竹竿的长为x米.
由题意,得x-322+32=x2,解得x=154.
10.5
11.解:(1)如图,连线AB,作AB的垂直平分线与AO交于点C,则点C即为所求.
(2)设BC为x海里,则CA=x海里,
∴OC=(45-x)海里.
∵OA⊥OB,∴∠O=90°,
∴在Rt△OBC中,OB2+OC2=BC2,
即152+(45-x)2=x2,解得x=25.
答:我国渔政船行驶的航程BC的长为25海里.
12.解:(1)CH⊥AB.
说明如下:在△CHB中,
∵CH2+BH2=2.42+1.82=9,
BC2=9,
∴CH2+BH2=BC2.
∴△CHB为直角三角形,且∠BHC=90°.
∴CH⊥AB.
(2)设AC=x千米.
在Rt△ACH中,由已知得AH=(x-1.8)千米,CH=2.4千米.
由勾股定理,得AC2=AH2+CH2,
∴x2=(x-1.8)2+2.42,
解得x=2.5.
答:原来的路AC的长为2.5千米.
13.解:(1)利用勾股定理求出信号的传送半径为1950米.
(2)小明所走的路程为39×30=3×13×30=1170(米),小华所走的路程为52×30=4×13×30=1560(米).
因为勾股数3,4,5的倍数仍能构成一组勾股数,故所求半径为5×13×30=1950(米).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
