第3 章勾股定理 单元自我综合评价---课时作业 2021-2022学年苏科版数学八年级上册(word版含答案)
文档属性
| 名称 | 第3 章勾股定理 单元自我综合评价---课时作业 2021-2022学年苏科版数学八年级上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 144.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 06:28:50 | ||
图片预览




文档简介
第3章 勾股定理 自我综合评价
一、选择题(每小题3分,共24分)
1.在Rt△ABC中,若斜边AB=4,则AC2+BC2等于( )
A.4 B.8 C.9 D.16
2.若a,b,c是△ABC的三边长,且满足(a-b)2=c2-2ab,则△ABC是( )
A.等腰三角形 B.直角三角形
C.等边三角形 D.等腰直角三角形
3.如,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )
A.4 B.6 C.16 D.55
4.一位工人师傅测量一个等腰三角形工件的腰、底边及底边上的高,并按顺序记录下数据,量完后,不小心与其他记录的数据混了,则下列数据中,可能是该等腰三角形工件的数据的是( )
A.13,10,10 B.13,10,12
C.13,12,12 D.13,10,11
5.如所示,已知AB=3 cm BC=4 cm,CD=12 cm,DA=13 cm,且AB⊥BC,则四边形ABCD的面积是( )
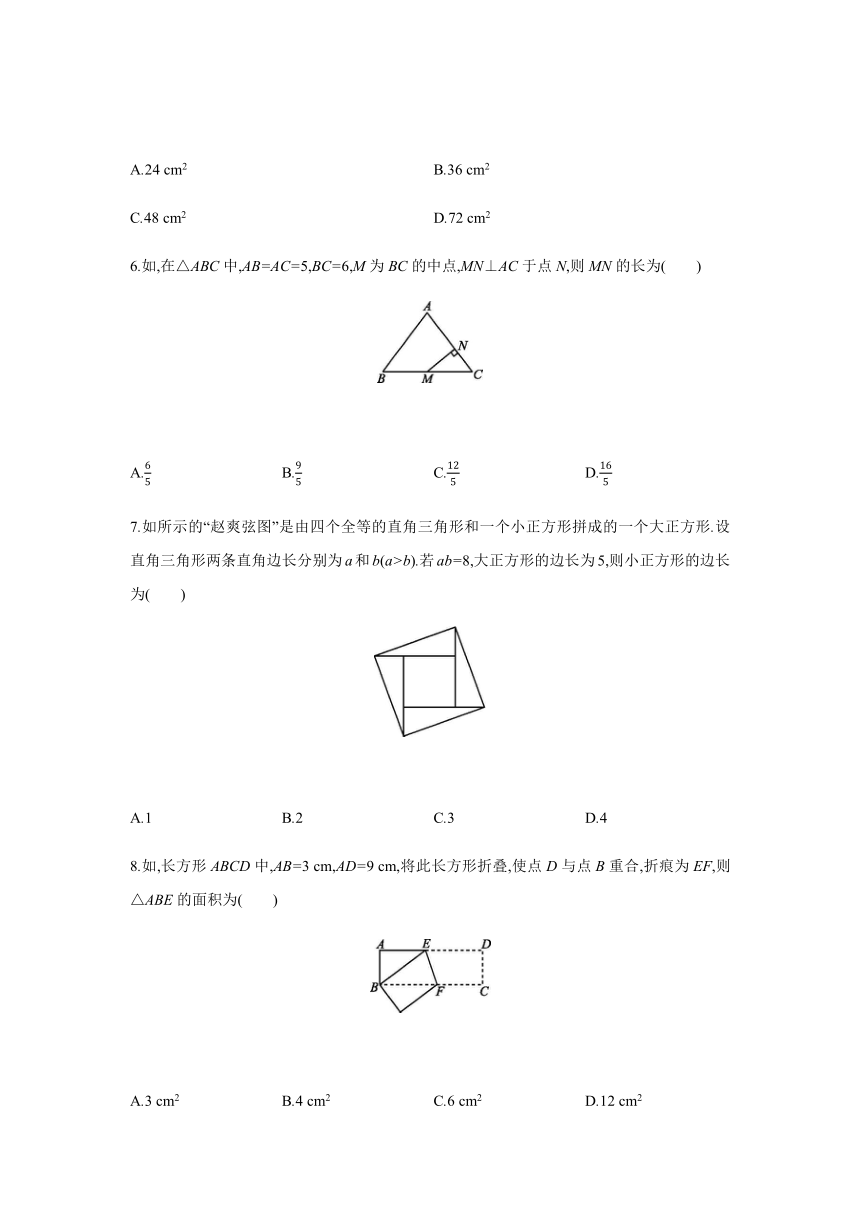
A.24 cm2 B.36 cm2
C.48 cm2 D.72 cm2
6.如,在△ABC中,AB=AC=5,BC=6,M为BC的中点,MN⊥AC于点N,则MN的长为( )
A.65 B.95 C.125 D.165
7.如所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形两条直角边长分别为a和b(a>b).若ab=8,大正方形的边长为5,则小正方形的边长为( )
A.1 B.2 C.3 D.4
8.如,长方形ABCD中,AB=3 cm,AD=9 cm,将此长方形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )
A.3 cm2 B.4 cm2 C.6 cm2 D.12 cm2
二、填空题(每小题4分,共28分)
9.在△ABC中,∠C=90°,若BC=6,AB=10,则AC= .?
10.一根高8 m的旗杆在下午3:00时的影长为6 m,此时旗杆的顶端与影子的顶端之间的距离是 m.?
11.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田的面积有多大.题中“里”是我国市制长度单位,1里=0.5千米,则该沙田的面积为 平方千米.?
12.如,在△ABC中,∠C=90°,AD平分∠CAB,AD=10 cm,AC=8 cm,那么点D到直线AB的距离是 cm.?
13.一直角三角形的三边长分别为6,8,x,那么以x为边长的正方形的面积为 .?
14.如,正方形网格中,每个小正方形的边长均为1,网格内有△PAB,则∠PAB+∠PBA的度数是 .(A,B,P都是网格线的交点)?
15.如,在Rt△ABC中,∠C=90°,AC=4,BC=3,现将BC延长到点D,使△ABD为等腰三角形,则CD的长为 .?
三、解答题(共48分)
16.(8分)已知△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
(1)若a∶b=3∶4,c=25,求a,b的值;
(2)若c-a=4,b=12,求a,c的值.
17.(6分)如,在△ABC中,CD⊥AB于点D,AC=20,BC=15,AD=16,求AB的长.
18.(10分)如,在吴中区上方山动物园里有两只猴子在一棵树CD上的点B处,且BC=5 m,它们都要到池塘A处吃东西,其中一只猴子甲沿树爬至C再沿CA走到离树24 m处的池塘A处,另一只猴子乙先爬到树顶D处后再沿缆绳DA滑到A处.已知猴子甲所经过的路程比猴子乙所经过的路程多2 m,设BD为x m.
(1)请用含有x的整式表示线段AD的长为 m;?
(2)求这棵树高多少米.
19.(10分)如,在△ABC中,边AB的垂直平分线交AB,BC于点M,E,边AC的垂直平分线交AC,BC于点N,F,△AEF的周长为10.
(1)求BC的长;
(2)若∠B+∠C=45°,EF=4,求△AEF的面积.
20.(14分)如,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B'处,点A落在点A'处.
(1)试说明:B'E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间有何等量关系,并说明理由.
教师详解详析
1.D [解析] ∵在Rt△ABC中,斜边AB=4,
∴AC2+BC2=16.故选D.
2.B [解析] ∵(a-b)2=c2-2ab.
∴a2+b2-2ab=c2-2ab,
∴a2+b2=c2.∴△ABC是直角三角形.
故选B.
3.C
4.B [解析] 由题可知,在等腰三角形中,底边的一半、底边上的高以及腰正好构成一个直角三角形,且1022+122=132,符合勾股定理.故选B.
5.B
6.C [解析] 连接AM.因为AB=AC,M是BC的中点,所以AM⊥BC.
在Rt△ABM中,AM2=AB2-BM2=16,
所以AM=4.
因为MN⊥AC,所以12MN·AC=12AM·MC.
所以 MN=125.
7.C [解析] 由题意可知,中间小正方形的边长为a-b,
∴4×12ab+(a-b)2=52,
∴(a-b)2=25-16=9.
∵小正方形的边长a-b>0,
∴a-b=3.
故选C.
8.C [解析] ∵将此长方形折叠,使点D与点B重合,
∴BE=DE.
∵AD=AE+DE=AE+BE=9 cm,
∴BE=9-AE.
根据勾股定理可知AB2+AE2=BE2,
即32+AE2=(9-AE)2,解得AE=4.
∴△ABE的面积为12×3×4=6(cm2).故选C.
9.8 [解析] ∵在△ABC中,∠C=90°,BC=6,AB=10,
∴AC2=AB2-BC2=102-62=64,
∴AC=8.
10.10
11.7.5 [解析] ∵52+122=132,∴这个三角形为直角三角形.∴这块沙田的面积为12×5×0.5×12×0.5=7.5(千米2).
12.6
13.100或28 [解析] 当较大的数8是直角边长时,根据勾股定理,得x2=36+64=100;
当较大的数8是斜边长时,根据勾股定理,得x2=64-36=28.
所以以x为边长的正方形的面积为100或28.
14.45° [解析] 如图,延长AP到点C,使PC=AP,连接BC.
∵AP2=PC2=12+22=5,
BC2=5,
BP2=12+32=10,
∴PC=BC,PC2+BC2=BP2,
∴△PCB是等腰直角三角形,
则∠CPB=∠CBP=45°,
∴∠PAB+∠PBA=∠CPB=45°.
故答案为45°.
15.3或2或76 [解析] 由于扩充所得的等腰三角形腰和底不确定,所以应分①AB=AD,②AB=BD,③AD=BD三种情况进行讨论.
16.解:(1)设a=3x,则b=4x.
∵a2+b2=c2,∴(3x)2+(4x)2=252.
解得x=5(负值已舍去),
∴a=15,b=20.
(2)由c-a=4,得c=4+a.
∵a2+b2=c2,
∴a2+122=(4+a)2,
解得a=16.∴c=20.
17.解:∵CD⊥AB于点D,
∴∠ADC=∠BDC=90°.
∵在Rt△ACD中,AC=20,AD=16,
∴CD2=AC2-AD2=202-162=144,
∴CD=12.
∵在Rt△BCD中,BC=15,CD=12,
∴BD2=BC2-CD2=152-122=81,
∴BD=9.
∴AB=AD+BD=25.
18.解:(1)(27-x)
(2)∵∠C=90°,∴AD2=AC2+CD2,
即(27-x)2=(x+5)2+242,解得x=2.
∴CD=5+2=7(m).
答:这棵树高7 m.
19.解:(1)∵边AB的垂直平分线交AB,BC于点M,E,
∴AE=BE.
∵边AC的垂直平分线交AC,BC于点N,F,
∴AF=FC.
∵△AEF的周长为10,
∴AE+EF+AF=BE+EF+FC=BC=10.
故BC=10.
(2)∵∠B+∠C=45°,
由(1)知∠B+∠C=∠BAE+∠FAC,
∴∠FAE=90°.
∵△AEF的周长为10,EF=4,
∴AE+AF=6.
∴(AE+AF)2=36,AE2+AF2=16,
∴AE·AF=10,
则△AEF的面积=12AE·AF=5.
20.解:(1)由题意,得B'F=BF,∠B'FE=∠BFE.
在长方形ABCD中,AD∥BC,
则∠B'EF=∠BFE,
所以∠B'FE=∠B'EF,
所以B'F=B'E.
故B'E=BF.
(2)猜想a,b,c之间存在关系:a2+b2=c2.
理由:由题意知A'E=AE,A'B'=AB.
由(1)知B'E=BF,
则在Rt△A'EB'中,∠A'=∠A=90°,A'E=a,
A'B'=b,B'E=c,
根据勾股定理,有a2+b2=c2.
一、选择题(每小题3分,共24分)
1.在Rt△ABC中,若斜边AB=4,则AC2+BC2等于( )
A.4 B.8 C.9 D.16
2.若a,b,c是△ABC的三边长,且满足(a-b)2=c2-2ab,则△ABC是( )
A.等腰三角形 B.直角三角形
C.等边三角形 D.等腰直角三角形
3.如,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )
A.4 B.6 C.16 D.55
4.一位工人师傅测量一个等腰三角形工件的腰、底边及底边上的高,并按顺序记录下数据,量完后,不小心与其他记录的数据混了,则下列数据中,可能是该等腰三角形工件的数据的是( )
A.13,10,10 B.13,10,12
C.13,12,12 D.13,10,11
5.如所示,已知AB=3 cm BC=4 cm,CD=12 cm,DA=13 cm,且AB⊥BC,则四边形ABCD的面积是( )
A.24 cm2 B.36 cm2
C.48 cm2 D.72 cm2
6.如,在△ABC中,AB=AC=5,BC=6,M为BC的中点,MN⊥AC于点N,则MN的长为( )
A.65 B.95 C.125 D.165
7.如所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形两条直角边长分别为a和b(a>b).若ab=8,大正方形的边长为5,则小正方形的边长为( )
A.1 B.2 C.3 D.4
8.如,长方形ABCD中,AB=3 cm,AD=9 cm,将此长方形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )
A.3 cm2 B.4 cm2 C.6 cm2 D.12 cm2
二、填空题(每小题4分,共28分)
9.在△ABC中,∠C=90°,若BC=6,AB=10,则AC= .?
10.一根高8 m的旗杆在下午3:00时的影长为6 m,此时旗杆的顶端与影子的顶端之间的距离是 m.?
11.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田的面积有多大.题中“里”是我国市制长度单位,1里=0.5千米,则该沙田的面积为 平方千米.?
12.如,在△ABC中,∠C=90°,AD平分∠CAB,AD=10 cm,AC=8 cm,那么点D到直线AB的距离是 cm.?
13.一直角三角形的三边长分别为6,8,x,那么以x为边长的正方形的面积为 .?
14.如,正方形网格中,每个小正方形的边长均为1,网格内有△PAB,则∠PAB+∠PBA的度数是 .(A,B,P都是网格线的交点)?
15.如,在Rt△ABC中,∠C=90°,AC=4,BC=3,现将BC延长到点D,使△ABD为等腰三角形,则CD的长为 .?
三、解答题(共48分)
16.(8分)已知△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
(1)若a∶b=3∶4,c=25,求a,b的值;
(2)若c-a=4,b=12,求a,c的值.
17.(6分)如,在△ABC中,CD⊥AB于点D,AC=20,BC=15,AD=16,求AB的长.
18.(10分)如,在吴中区上方山动物园里有两只猴子在一棵树CD上的点B处,且BC=5 m,它们都要到池塘A处吃东西,其中一只猴子甲沿树爬至C再沿CA走到离树24 m处的池塘A处,另一只猴子乙先爬到树顶D处后再沿缆绳DA滑到A处.已知猴子甲所经过的路程比猴子乙所经过的路程多2 m,设BD为x m.
(1)请用含有x的整式表示线段AD的长为 m;?
(2)求这棵树高多少米.
19.(10分)如,在△ABC中,边AB的垂直平分线交AB,BC于点M,E,边AC的垂直平分线交AC,BC于点N,F,△AEF的周长为10.
(1)求BC的长;
(2)若∠B+∠C=45°,EF=4,求△AEF的面积.
20.(14分)如,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B'处,点A落在点A'处.
(1)试说明:B'E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间有何等量关系,并说明理由.
教师详解详析
1.D [解析] ∵在Rt△ABC中,斜边AB=4,
∴AC2+BC2=16.故选D.
2.B [解析] ∵(a-b)2=c2-2ab.
∴a2+b2-2ab=c2-2ab,
∴a2+b2=c2.∴△ABC是直角三角形.
故选B.
3.C
4.B [解析] 由题可知,在等腰三角形中,底边的一半、底边上的高以及腰正好构成一个直角三角形,且1022+122=132,符合勾股定理.故选B.
5.B
6.C [解析] 连接AM.因为AB=AC,M是BC的中点,所以AM⊥BC.
在Rt△ABM中,AM2=AB2-BM2=16,
所以AM=4.
因为MN⊥AC,所以12MN·AC=12AM·MC.
所以 MN=125.
7.C [解析] 由题意可知,中间小正方形的边长为a-b,
∴4×12ab+(a-b)2=52,
∴(a-b)2=25-16=9.
∵小正方形的边长a-b>0,
∴a-b=3.
故选C.
8.C [解析] ∵将此长方形折叠,使点D与点B重合,
∴BE=DE.
∵AD=AE+DE=AE+BE=9 cm,
∴BE=9-AE.
根据勾股定理可知AB2+AE2=BE2,
即32+AE2=(9-AE)2,解得AE=4.
∴△ABE的面积为12×3×4=6(cm2).故选C.
9.8 [解析] ∵在△ABC中,∠C=90°,BC=6,AB=10,
∴AC2=AB2-BC2=102-62=64,
∴AC=8.
10.10
11.7.5 [解析] ∵52+122=132,∴这个三角形为直角三角形.∴这块沙田的面积为12×5×0.5×12×0.5=7.5(千米2).
12.6
13.100或28 [解析] 当较大的数8是直角边长时,根据勾股定理,得x2=36+64=100;
当较大的数8是斜边长时,根据勾股定理,得x2=64-36=28.
所以以x为边长的正方形的面积为100或28.
14.45° [解析] 如图,延长AP到点C,使PC=AP,连接BC.
∵AP2=PC2=12+22=5,
BC2=5,
BP2=12+32=10,
∴PC=BC,PC2+BC2=BP2,
∴△PCB是等腰直角三角形,
则∠CPB=∠CBP=45°,
∴∠PAB+∠PBA=∠CPB=45°.
故答案为45°.
15.3或2或76 [解析] 由于扩充所得的等腰三角形腰和底不确定,所以应分①AB=AD,②AB=BD,③AD=BD三种情况进行讨论.
16.解:(1)设a=3x,则b=4x.
∵a2+b2=c2,∴(3x)2+(4x)2=252.
解得x=5(负值已舍去),
∴a=15,b=20.
(2)由c-a=4,得c=4+a.
∵a2+b2=c2,
∴a2+122=(4+a)2,
解得a=16.∴c=20.
17.解:∵CD⊥AB于点D,
∴∠ADC=∠BDC=90°.
∵在Rt△ACD中,AC=20,AD=16,
∴CD2=AC2-AD2=202-162=144,
∴CD=12.
∵在Rt△BCD中,BC=15,CD=12,
∴BD2=BC2-CD2=152-122=81,
∴BD=9.
∴AB=AD+BD=25.
18.解:(1)(27-x)
(2)∵∠C=90°,∴AD2=AC2+CD2,
即(27-x)2=(x+5)2+242,解得x=2.
∴CD=5+2=7(m).
答:这棵树高7 m.
19.解:(1)∵边AB的垂直平分线交AB,BC于点M,E,
∴AE=BE.
∵边AC的垂直平分线交AC,BC于点N,F,
∴AF=FC.
∵△AEF的周长为10,
∴AE+EF+AF=BE+EF+FC=BC=10.
故BC=10.
(2)∵∠B+∠C=45°,
由(1)知∠B+∠C=∠BAE+∠FAC,
∴∠FAE=90°.
∵△AEF的周长为10,EF=4,
∴AE+AF=6.
∴(AE+AF)2=36,AE2+AF2=16,
∴AE·AF=10,
则△AEF的面积=12AE·AF=5.
20.解:(1)由题意,得B'F=BF,∠B'FE=∠BFE.
在长方形ABCD中,AD∥BC,
则∠B'EF=∠BFE,
所以∠B'FE=∠B'EF,
所以B'F=B'E.
故B'E=BF.
(2)猜想a,b,c之间存在关系:a2+b2=c2.
理由:由题意知A'E=AE,A'B'=AB.
由(1)知B'E=BF,
则在Rt△A'EB'中,∠A'=∠A=90°,A'E=a,
A'B'=b,B'E=c,
根据勾股定理,有a2+b2=c2.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
