第6 章 一次函数 单元小结与思考---课时作业 2021-2022学年苏科版数学八年级上册(word版含答案)
文档属性
| 名称 | 第6 章 一次函数 单元小结与思考---课时作业 2021-2022学年苏科版数学八年级上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 162.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 06:31:13 | ||
图片预览



文档简介
第6章 一次函数 自我综合评价
一、选择题(每小题4分,共24分)
1.下列函数中,是正比例函数的是( )
A.y=-3x+2 B.y=2x C.y=2x D.y=2x+1
2.根据如所示的程序计算函数y的值,若输入x的值是7,则输出y的值是-2,若输入x的值是-8,则输出y的值是( )
A.5 B.10 C.19 D.21
3.一次函数y=kx+b的图像如所示,则该一次函数的表达式为( )
A.y=-23x-2 B.y=23x-2
C.y=-23x+2 D.y=23x+2
4.如,一次函数y=kx+b(k,b为常数,且k≠0)的图像过点A(0,-1),B(1,1),则不等式kx+b>1的解集为( )
A.x>0 B.x<0 C.x>1 D.x<1
5.小刚以400米/分的速度匀速骑车5分钟,然后在原地休息了6分钟,最后以500米/分的速度骑回出发地.下列函数图像能表达这一过程的是( )
6.已知一次函数y1=ax+b和y2=bx+a(a≠b),则函数y1和y2的图像可能是( )
二、填空题(每小题4分,共24分)
7.若函数y=4x+3-a是正比例函数,则a= .?
8.直线y=-x-3向上平移2个单位长度后得到的直线的函数表达式是 .?
9.商品的销售量也受销售价格的影响,比如,某衬衣定价为每件100元时,每月可卖出2000件,每件的价格每上涨10元,销售量便减少50件.那么,每月售出衬衣的总件数y(件)与每件衬衣的价格x(元)之间的函数表达式为 .?
10.已知一次函数y=2x-1的图像经过A(x1,1),B(x2,3)两点,则x1 x2(填“>”“<”或“=”).?
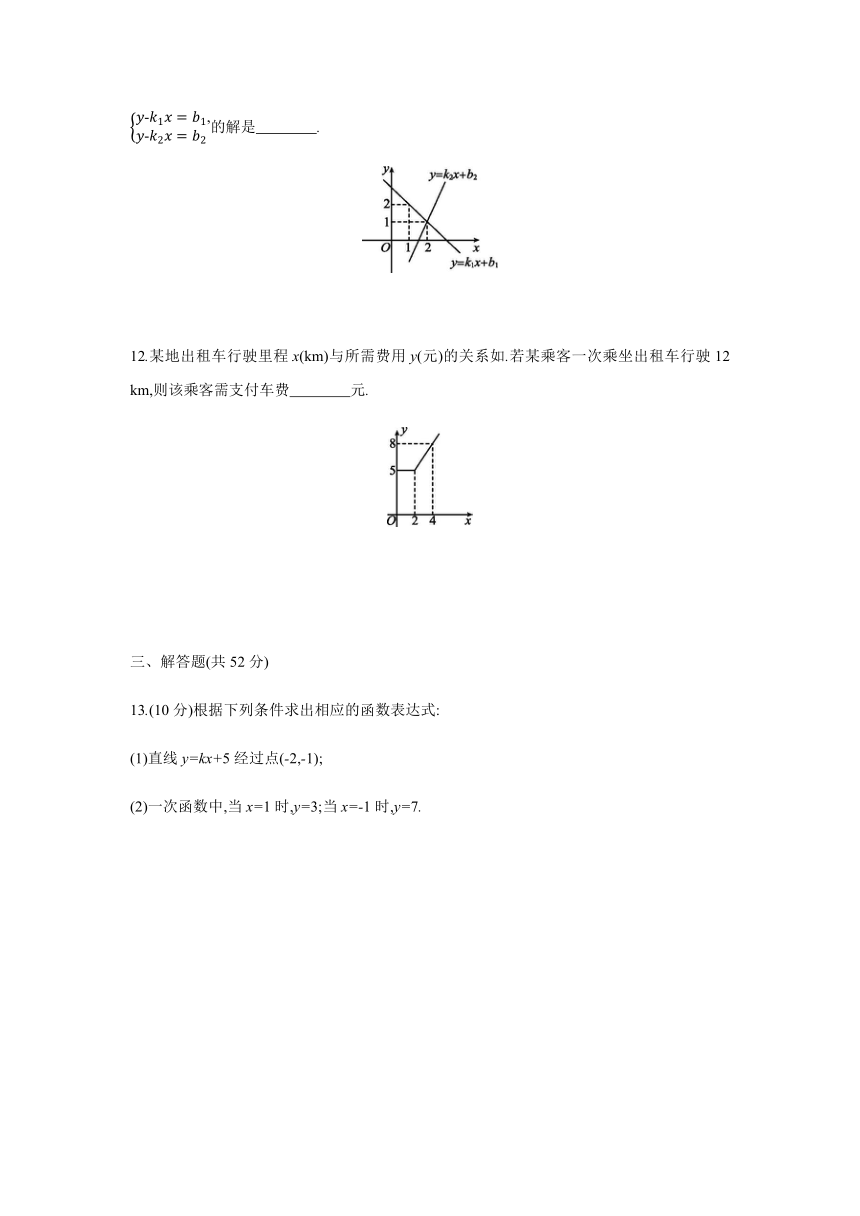
11.在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图像如所示,则关于x,y的方程组y-k1x=b1,y-k2x=b2的解是 .?
12.某地出租车行驶里程x(km)与所需费用y(元)的关系如.若某乘客一次乘坐出租车行驶12 km,则该乘客需支付车费 元.?
三、解答题(共52分)
13.(10分)根据下列条件求出相应的函数表达式:
(1)直线y=kx+5经过点(-2,-1);
(2)一次函数中,当x=1时,y=3;当x=-1时,y=7.
14.(12分)如,已知过点B(1,0)的直线l1与直线l2:y=2x+4相交于点P(-1,a).
(1)求直线l1的表达式;
(2)求四边形PAOC的面积.
15.(14分)某销售商准备采购一批儿童玩具,有A,B两种品牌可供选择,其进价和售价如下:
A品牌
B品牌
进价(元/件)
150
120
售价(元/件)
200
150
销售商购进A,B两种品牌的儿童玩具共30件.
(1)若销售商购进A品牌的儿童玩具为x(件),求销售商售完这30件儿童玩具获得的总利润y(元)与x之间的函数表达式;
(2)若想使得销售完这30件儿童玩具获得的总利润为1300元,则应购进A品牌的儿童玩具多少件?
16.(16分)用充电器给某手机充电时,其屏幕的起始画面如①.
经测试,在用快速充电器和普通充电器对该手机充电时,其电量E(单位:%)与充电时间t(单位:h)的函数图像分别为图②中的线段AB,AC.
根据以上信息,回答下列问题:
(1)在目前电量20%的情况下,用充电器给该手机充满电时,快速充电器比普通充电器少用多少小时?
(2)求线段AB,AC对应的函数表达式;
(3)已知该手机正常使用时耗电量为每小时10%,在用快速充电器将其充满电后,正常使用a h,接着再用普通充电器将其充满电,其“充电-耗电-充电”的时间恰好是6 h,求a的值.
教师详解详析
1.C
2.C [解析] 当x=7时,可得-7+b2=-2,解得b=3;当x=-8时,可得y=-2×(-8)+3=19.故选C.
3.B [解析] 把(0,-2)与(3,0)代入y=kx+b,得b=-2,3k+b=0,解得k=23,b=-2.
则一次函数表达式为y=23x-2.
故选B.
4.C 5.C 6.A 7.3
8.y=-x-1 [解析] 直线y=-x-3向上平移2个单位长度后得到直线y=-x-3+2,即y=-x-1.
9.y=-5x+2500 [解析] 由题意得,衬衣每件的价格每上涨1元,月销售量就减少5件,则每月售出衬衣的总件数y(件)与每件衬衣的价格x(元)之间的函数表达式为y=2000-5(x-100)=-5x+2500.
10.< [解析] ∵k=2>0,∴y随x的增大而增大.又∵1<3,∴x1 11.x=2,y=1 [解析] ∵一次函数y=k1x+b1与y=k2x+b2的图像的交点坐标为(2,1),∴关于x,y的方程组y-k1x=b1,y-k2x=b2的解是x=2,y=1.
12.20 [解析] 由图像知,当x≥2时,y与x之间的函数关系为一次函数,并且经过点(2,5),(4,8),
设该一次函数的表达式为y=kx+b,则有5=2k+b,8=4k+b,解得k=32,b=2,∴y=32x+2.
将x=12代入一次函数表达式,得y=18+2=20,故该乘客需支付车费20元.
13.解:(1)把(-2,-1)代入y=kx+5,得-2k+5=-1,解得k=3,
所以直线的函数表达式为y=3x+5.
(2)设一次函数表达式为y=ax+b.由题意,得
a+b=3,-a+b=7,解得a=-2,b=5.
所以一次函数表达式为y=-2x+5.
14.解:(1)∵点P(-1,a)在直线l2:y=2x+4上,
∴2×(-1)+4=a,即a=2,
则点P的坐标为(-1,2).
设直线l1的表达式为y=kx+b(k≠0),
则k+b=0,-k+b=2,解得k=-1,b=1.
∴直线l1的表达式为y=-x+1.
(2)∵直线l1与y轴相交于点C,
∴点C的坐标为(0,1).
又∵直线l2与x轴相交于点A,
∴点A的坐标为(-2,0),
则AB=3,而S四边形PAOC=S△PAB-S△BOC,
∴S四边形PAOC=12×3×2-12×1×1=52.
15.解:(1)由题意可得y=(200-150)x+(150-120)(30-x)=20x+900,
∴销售商售完这30件儿童玩具获得的总利润y(元)与x之间的函数表达式为y=20x+900.
(2)当y=1300时,即1300=20x+900,
解得x=20.
答:应购进A品牌的儿童玩具20件.
16.解:(1)由图像可知,在目前电量20%的情况下,快速充电器给该手机充满电需2 h,普通充电器给该手机充满电需6 h,
∴在目前电量20%的情况下,用充电器给该手机充满电时,快速充电器比普通充电器少用4 h.
(2)设线段AB对应的函数表达式为E1=k1t+b1.
将(0,20),(2,100)代入E1=k1t+b1,可得
b1=20,2k1+b1=100,解得k1=40,b1=20.
∴线段AB对应的函数表达式为E1=40t+20.
设线段AC对应的函数表达式为E2=k2t+b2,
将(0,20),(6,100)代入E2=k2t+b2,可得
b2=20,6k2+b2=100,解得k2=403,b2=20.
∴线段AC对应的函数表达式为E2=403t+20.
(3)根据题意,得403×(6-2-a)=10a,
解得a=167.
一、选择题(每小题4分,共24分)
1.下列函数中,是正比例函数的是( )
A.y=-3x+2 B.y=2x C.y=2x D.y=2x+1
2.根据如所示的程序计算函数y的值,若输入x的值是7,则输出y的值是-2,若输入x的值是-8,则输出y的值是( )
A.5 B.10 C.19 D.21
3.一次函数y=kx+b的图像如所示,则该一次函数的表达式为( )
A.y=-23x-2 B.y=23x-2
C.y=-23x+2 D.y=23x+2
4.如,一次函数y=kx+b(k,b为常数,且k≠0)的图像过点A(0,-1),B(1,1),则不等式kx+b>1的解集为( )
A.x>0 B.x<0 C.x>1 D.x<1
5.小刚以400米/分的速度匀速骑车5分钟,然后在原地休息了6分钟,最后以500米/分的速度骑回出发地.下列函数图像能表达这一过程的是( )
6.已知一次函数y1=ax+b和y2=bx+a(a≠b),则函数y1和y2的图像可能是( )
二、填空题(每小题4分,共24分)
7.若函数y=4x+3-a是正比例函数,则a= .?
8.直线y=-x-3向上平移2个单位长度后得到的直线的函数表达式是 .?
9.商品的销售量也受销售价格的影响,比如,某衬衣定价为每件100元时,每月可卖出2000件,每件的价格每上涨10元,销售量便减少50件.那么,每月售出衬衣的总件数y(件)与每件衬衣的价格x(元)之间的函数表达式为 .?
10.已知一次函数y=2x-1的图像经过A(x1,1),B(x2,3)两点,则x1 x2(填“>”“<”或“=”).?
11.在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图像如所示,则关于x,y的方程组y-k1x=b1,y-k2x=b2的解是 .?
12.某地出租车行驶里程x(km)与所需费用y(元)的关系如.若某乘客一次乘坐出租车行驶12 km,则该乘客需支付车费 元.?
三、解答题(共52分)
13.(10分)根据下列条件求出相应的函数表达式:
(1)直线y=kx+5经过点(-2,-1);
(2)一次函数中,当x=1时,y=3;当x=-1时,y=7.
14.(12分)如,已知过点B(1,0)的直线l1与直线l2:y=2x+4相交于点P(-1,a).
(1)求直线l1的表达式;
(2)求四边形PAOC的面积.
15.(14分)某销售商准备采购一批儿童玩具,有A,B两种品牌可供选择,其进价和售价如下:
A品牌
B品牌
进价(元/件)
150
120
售价(元/件)
200
150
销售商购进A,B两种品牌的儿童玩具共30件.
(1)若销售商购进A品牌的儿童玩具为x(件),求销售商售完这30件儿童玩具获得的总利润y(元)与x之间的函数表达式;
(2)若想使得销售完这30件儿童玩具获得的总利润为1300元,则应购进A品牌的儿童玩具多少件?
16.(16分)用充电器给某手机充电时,其屏幕的起始画面如①.
经测试,在用快速充电器和普通充电器对该手机充电时,其电量E(单位:%)与充电时间t(单位:h)的函数图像分别为图②中的线段AB,AC.
根据以上信息,回答下列问题:
(1)在目前电量20%的情况下,用充电器给该手机充满电时,快速充电器比普通充电器少用多少小时?
(2)求线段AB,AC对应的函数表达式;
(3)已知该手机正常使用时耗电量为每小时10%,在用快速充电器将其充满电后,正常使用a h,接着再用普通充电器将其充满电,其“充电-耗电-充电”的时间恰好是6 h,求a的值.
教师详解详析
1.C
2.C [解析] 当x=7时,可得-7+b2=-2,解得b=3;当x=-8时,可得y=-2×(-8)+3=19.故选C.
3.B [解析] 把(0,-2)与(3,0)代入y=kx+b,得b=-2,3k+b=0,解得k=23,b=-2.
则一次函数表达式为y=23x-2.
故选B.
4.C 5.C 6.A 7.3
8.y=-x-1 [解析] 直线y=-x-3向上平移2个单位长度后得到直线y=-x-3+2,即y=-x-1.
9.y=-5x+2500 [解析] 由题意得,衬衣每件的价格每上涨1元,月销售量就减少5件,则每月售出衬衣的总件数y(件)与每件衬衣的价格x(元)之间的函数表达式为y=2000-5(x-100)=-5x+2500.
10.< [解析] ∵k=2>0,∴y随x的增大而增大.又∵1<3,∴x1
12.20 [解析] 由图像知,当x≥2时,y与x之间的函数关系为一次函数,并且经过点(2,5),(4,8),
设该一次函数的表达式为y=kx+b,则有5=2k+b,8=4k+b,解得k=32,b=2,∴y=32x+2.
将x=12代入一次函数表达式,得y=18+2=20,故该乘客需支付车费20元.
13.解:(1)把(-2,-1)代入y=kx+5,得-2k+5=-1,解得k=3,
所以直线的函数表达式为y=3x+5.
(2)设一次函数表达式为y=ax+b.由题意,得
a+b=3,-a+b=7,解得a=-2,b=5.
所以一次函数表达式为y=-2x+5.
14.解:(1)∵点P(-1,a)在直线l2:y=2x+4上,
∴2×(-1)+4=a,即a=2,
则点P的坐标为(-1,2).
设直线l1的表达式为y=kx+b(k≠0),
则k+b=0,-k+b=2,解得k=-1,b=1.
∴直线l1的表达式为y=-x+1.
(2)∵直线l1与y轴相交于点C,
∴点C的坐标为(0,1).
又∵直线l2与x轴相交于点A,
∴点A的坐标为(-2,0),
则AB=3,而S四边形PAOC=S△PAB-S△BOC,
∴S四边形PAOC=12×3×2-12×1×1=52.
15.解:(1)由题意可得y=(200-150)x+(150-120)(30-x)=20x+900,
∴销售商售完这30件儿童玩具获得的总利润y(元)与x之间的函数表达式为y=20x+900.
(2)当y=1300时,即1300=20x+900,
解得x=20.
答:应购进A品牌的儿童玩具20件.
16.解:(1)由图像可知,在目前电量20%的情况下,快速充电器给该手机充满电需2 h,普通充电器给该手机充满电需6 h,
∴在目前电量20%的情况下,用充电器给该手机充满电时,快速充电器比普通充电器少用4 h.
(2)设线段AB对应的函数表达式为E1=k1t+b1.
将(0,20),(2,100)代入E1=k1t+b1,可得
b1=20,2k1+b1=100,解得k1=40,b1=20.
∴线段AB对应的函数表达式为E1=40t+20.
设线段AC对应的函数表达式为E2=k2t+b2,
将(0,20),(6,100)代入E2=k2t+b2,可得
b2=20,6k2+b2=100,解得k2=403,b2=20.
∴线段AC对应的函数表达式为E2=403t+20.
(3)根据题意,得403×(6-2-a)=10a,
解得a=167.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
