2021—2022学年苏科版八年级数学上册2.5等腰三角形的轴对称性 同步专题提升训练 (word版含答案解析)
文档属性
| 名称 | 2021—2022学年苏科版八年级数学上册2.5等腰三角形的轴对称性 同步专题提升训练 (word版含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 492.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 10:46:52 | ||
图片预览



文档简介
2021年苏科版八年级数学上册《2.5等腰三角形的轴对称性》同步专题提升训练(附答案)
1.在等边△ABC所在的平面内求一点P,使△PAB、△PBC、△PAC都是等腰三角形,具有这样性质的点P有( )
A.1个 B.4个 C.7个 D.10个
2.如图所示,△ABC是等边三角形,且BD=CE,∠1=15°,则∠2的度数为( )
A.15° B.30° C.45° D.60°
3.如图,△ABC是等边三角形,BC=BD,∠BAD=20°,则∠BCD的度数为( )
A.50° B.55° C.60° D.65°
4.下列条件不能得到等边三角形的是( )
A.有两个内角是60°的三角形 B.有一个角是60°的等腰三角形
C.腰和底相等的等腰三角形 D.有两个角相等的等腰三角形
5.如图,四边形ABCD中,CD=3,AD=5,AC的垂直平分线交AD于E,则△CDE的周长是( )
A.6 B.8 C.9 D.10
6.如图,在四边形ABCD中,∠A=∠B=60°,∠D=90°,AB=2,则CD长的取值范围是( )
A.<CD< B.CD>2 C.1<CD<2 D.0<CD<
7.如图,在正方体的两个面上画了两条对角线AB,AC,则∠BAC等于( )
A.60° B.75° C.90° D.135°
8.如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )
A.18° B.20° C.25° D.15°
9.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.其中正确的结论的个数是( )
A.2个 B.3个 C.4个 D.5个
10.如图等边三角形ABC中,AB=AC=BC=10cm,DC=4cm.点M、N都以3cm/s的速度运动,点M在线段CB上由点C向点B运动,点N在线段BA上由点B向点A运动.它们同时出发,当两点运动时间为t秒时,△BMN是一个直角三角形,则t的值( )
A. B. C.或 D.或
11.如图,点O是边长为2的等边三角形ABC内任意一点,且OD⊥AC,OE⊥AB,OF⊥BC,则OD+OE+OF= .
12.如图,在正△ABC中,点D在边AB上,点E在边AC上,将△ADE折叠,使点A落在BC边上的点F处,则∠BDF+∠CEF= .
13.如图,直线a,b过等边三角形ABC顶点A和C,且a∥b,∠1=42°,则∠2的度数为 .
14.在下列结论中:①有三个角是60°的三角形是等边三角形;②有一个外角是120°的等腰三角形是等边三角形;③有一个角是60°,且是轴对称的三角形是等边三角形;④有一腰上的高也是这腰上的中线的等腰三角形是等边三角形.其中正确的是 .
15.如图,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=9cm,DE=3cm,则BC= cm.
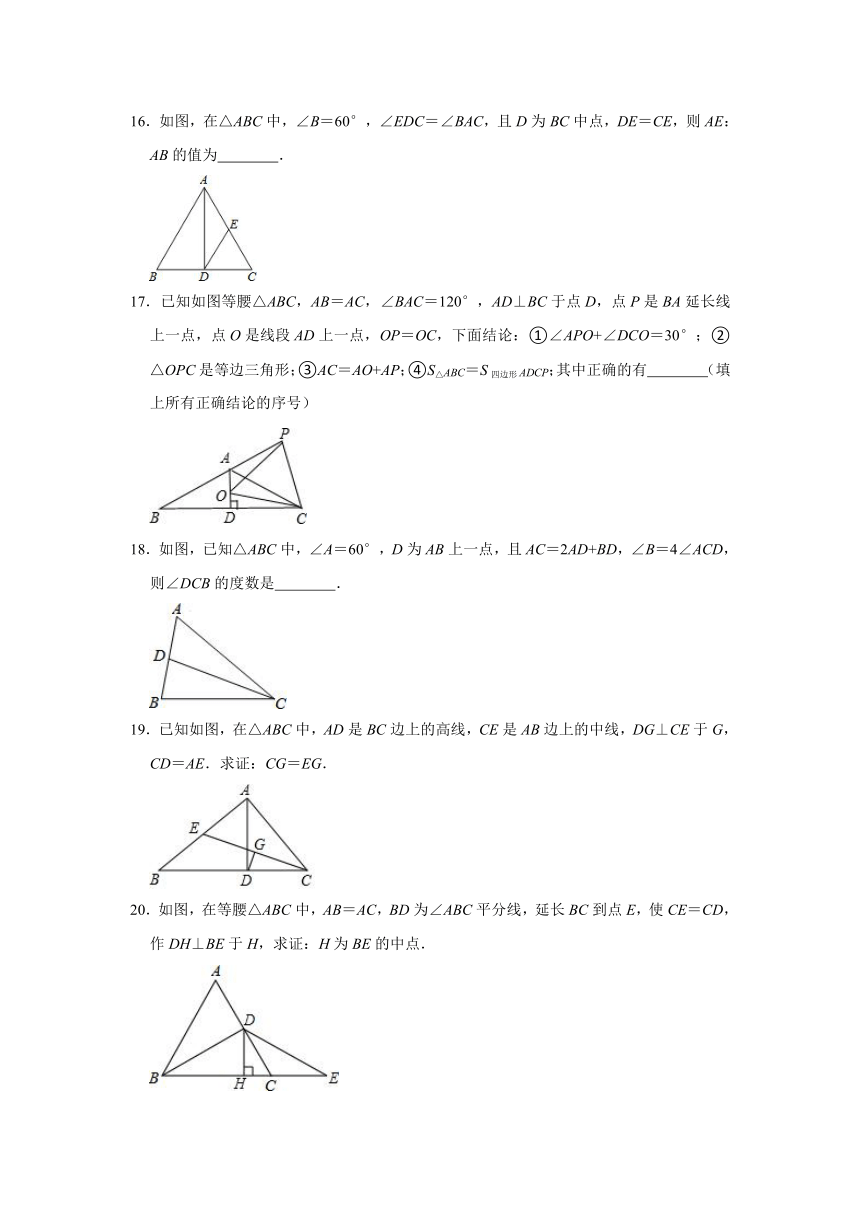
16.如图,在△ABC中,∠B=60°,∠EDC=∠BAC,且D为BC中点,DE=CE,则AE:AB的值为 .
17.已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形ADCP;其中正确的有 (填上所有正确结论的序号)
18.如图,已知△ABC中,∠A=60°,D为AB上一点,且AC=2AD+BD,∠B=4∠ACD,则∠DCB的度数是 .
19.已知如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.求证:CG=EG.
20.如图,在等腰△ABC中,AB=AC,BD为∠ABC平分线,延长BC到点E,使CE=CD,作DH⊥BE于H,求证:H为BE的中点.
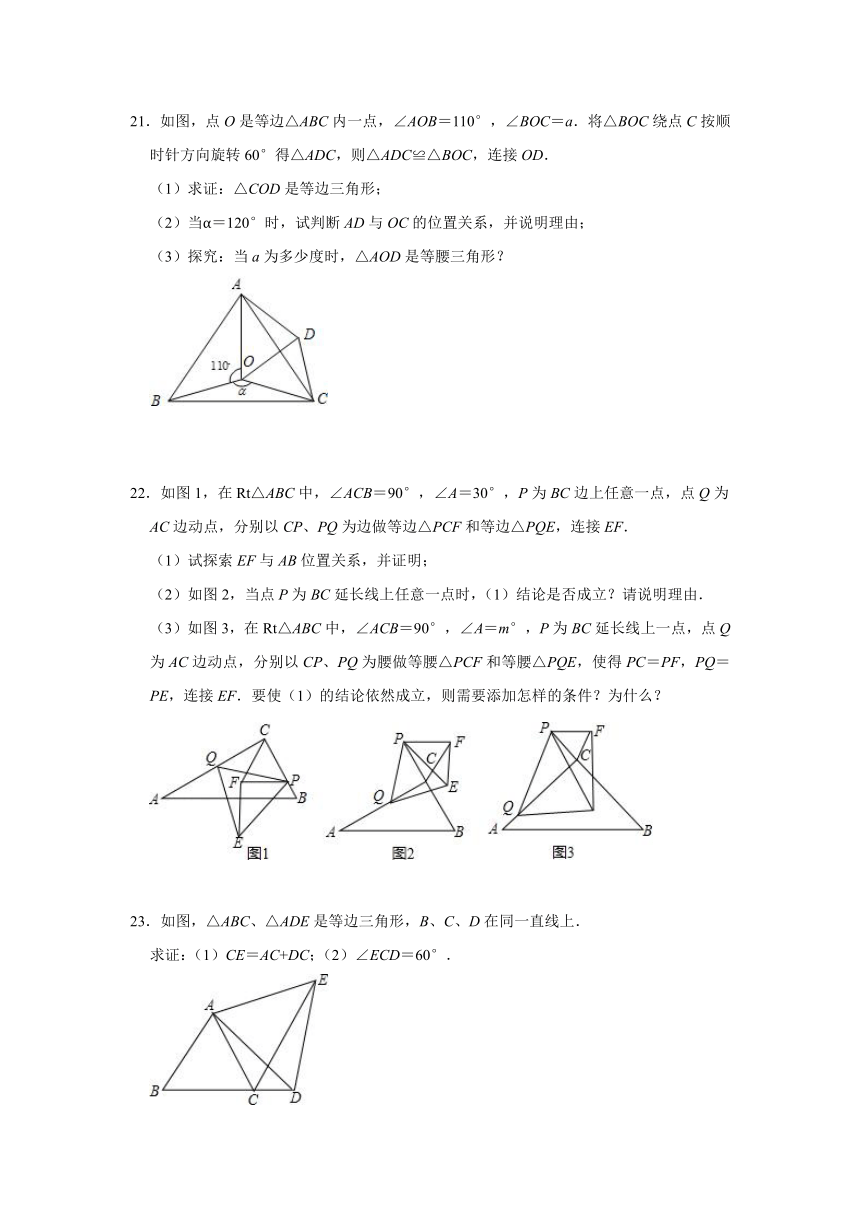
21.如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,则△ADC≌△BOC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=120°时,试判断AD与OC的位置关系,并说明理由;
(3)探究:当a为多少度时,△AOD是等腰三角形?
22.如图1,在Rt△ABC中,∠ACB=90°,∠A=30°,P为BC边上任意一点,点Q为AC边动点,分别以CP、PQ为边做等边△PCF和等边△PQE,连接EF.
(1)试探索EF与AB位置关系,并证明;
(2)如图2,当点P为BC延长线上任意一点时,(1)结论是否成立?请说明理由.
(3)如图3,在Rt△ABC中,∠ACB=90°,∠A=m°,P为BC延长线上一点,点Q为AC边动点,分别以CP、PQ为腰做等腰△PCF和等腰△PQE,使得PC=PF,PQ=PE,连接EF.要使(1)的结论依然成立,则需要添加怎样的条件?为什么?
23.如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.
求证:(1)CE=AC+DC;(2)∠ECD=60°.
24.如图1,已知线段AB的长为2a,点P是AB上的动点(P不与A,B重合),分别以AP、PB为边向线段AB的同一侧作正△APC和正△PBD.
(1)当△APC与△PBD的面积之和取最小值时,AP= ;(直接写结果)
(2)连接AD、BC,相交于点Q,设∠AQC=α,那么α的大小是否会随点P的移动而变化?请说明理由;
(3)如图2,若点P固定,将△PBD绕点P按顺时针方向旋转(旋转角小于180°),此时α的大小是否发生变化?(只需直接写出你的猜想,不必证明)
25.在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系.
(1)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是 ;此时= ;
(2)如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想(I)问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.
(3)如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.
26.学完“几何的回顾”一章后,老师布置了一道思考题:
如图,点M,N分别在正三角形ABC的BC,CA边上,且BM=CN,AM,BN交于点Q.求证:∠BQM=60度.
(1)请你完成这道思考题;
(2)做完(1)后,同学们在老师的启发下进行了反思,提出了许多问题,如:
①若将题中“BM=CN”与“∠BQM=60°”的位置交换,得到的是否仍是真命题?
②若将题中的点M,N分别移动到BC,CA的延长线上,是否仍能得到∠BQM=60°?
③若将题中的条件“点M,N分别在正三角形ABC的BC,CA边上”改为“点M,N分别在正方形ABCD的BC,CD边上”,是否仍能得到∠BQM=60°?…
请你作出判断,在下列横线上填写“是”或“否”:① ;② ;③ .并对②,③的判断,选择一个给出证明.
27.已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC的距离分别为h1,h2,h3,△ABC的高为h.
(1)若点P在一边BC上[如图①],此时h3=0,求证:h1+h2+h3=h;
(2)当点P在△ABC内[如图②],以及点P在△ABC外[如图③]这两种情况时,上述结论是否成立?若成立,请予以证明;若不成立,h1,h2,h3与h之间又有怎样的关系,请说出你的猜想,并说明理由.
参考答案
1.解:(1)点P在三角形内部时,点P是边AB、BC、CA的垂直平分线的交点,是三角形的外心;
(2)分别以三角形各顶点为圆心,边长为半径,交垂直平分线的交点就是满足要求的.每条垂直平分线上得3个交点,再加三角形的垂心,一共10个.故具有这种性质的点P共有10个.故选:D.
2.解:在△ABD和△BCE中,
,
∴△ABD≌△BCE,
∴∠1=∠CBE,
∵∠2=∠1+∠ABE,
∴∠2=∠CBE+∠ABE=∠ABC=60°.
故选:D.
3.解:∵△ABC是等边三角形,
∴∠ABC=60°,AB=BC,
∵BC=BD,
∴AB=BD,
∴∠BAD=∠BDA=20°,
∴∠ABD=180°﹣20°﹣20°=140°,
∴∠CBD=80°,
∴∠BCD=∠BDC=(180°﹣80°)=50°,故选:A.
4.解:A、有两个内角是60°的三角形是等边三角形,不符合题意;
B、有一个角是60°的等腰三角形是等边三角形,不符合题意;
C、腰和底相等的等腰三角形是等边三角形,不符合题意;
D、有两个角相等的等腰三角形可能不是等边三角形,符合题意;故选:D.
5.解:∵AC的垂直平分线交AD于E,
∴AE=CE,
∴△CDE的周长是:DE+CD+CE=DC+DE+AE=DC+AD=3+5=8.
故选:B.
6.解:延长AD,BC交于E,
∵∠A=∠B=60°,
∴△ABE是等边三角形,
过B作BF⊥AE于F,
∵AB=2,
∴BF=,
∵∠D=90°,
∴CD∥BF,
∴CD长的取值范围是0<CD<,故选:D.
7.解:连接BC,如图,
∵AB、AC和BC都是正方体的三个面的对角线,
∴AB=AC=BC,
∴△ABC为等边三角形,
∴∠BAC=60°.故选:A.
8.解:如图延长BD到M使得DM=DC,
∵∠ADB=78°,
∴∠ADM=180°﹣∠ADB=102°,
∵∠ADB=78°,∠BDC=24°,
∴∠ADC=∠ADB+∠BDC=102°,
∴∠ADM=∠ADC,
在△ADM和△ADC中,
,
∴△ADM≌△ADC,
∴AM=AC=AB,
∵∠ABD=60°,
∴△AMB是等边三角形,
∴∠M=∠DCA=60°,
∵∠DOC=∠AOB,∠DCO=∠ABO=60°,
∴∠BAO=∠ODC=24°,
∵∠CAB+∠ABC+∠ACB=180°,
∴24°+2(60°+∠CBD)=180°,
∴∠CBD=18°,故选:A.
9.解:①△ABC和△DCE均是等边三角形,点A,C,E在同一条直线上,
∴AC=BC,EC=DC,∠BCE=∠ACD=120°
∴△ACD≌△ECB
∴AD=BE,故本选项正确;
②∵△ACD≌△ECB
∴∠CBQ=∠CAP,
又∵∠PCQ=∠ACB=60°,CB=AC,
∴△BCQ≌△ACP,
∴CQ=CP,又∠PCQ=60°,
∴△PCQ为等边三角形,
∴∠QPC=60°=∠ACB,
∴PQ∥AE,故本选项正确;
③∵∠ACB=∠DCE=60°,
∴∠BCD=60°,
∴∠ACP=∠BCQ,
∵AC=BC,∠DAC=∠QBC,
∴△ACP≌△BCQ(ASA),
∴CP=CQ,AP=BQ,故本选项正确;
④已知△ABC、△DCE为正三角形,
故∠DCE=∠BCA=60°?∠DCB=60°,
又因为∠DPC=∠DAC+∠BCA,∠BCA=60°?∠DPC>60°,
故DP不等于DE,故本选项错误;
⑤∵△ABC、△DCE为正三角形,
∴∠ACB=∠DCE=60°,AC=BC,DC=EC,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
∴∠AOB=∠CAD+∠CEB=∠CBE+∠CEB,
∵∠ACB=∠CBE+∠CEB=60°,
∴∠AOB=60°,
故本选项正确.
综上所述,正确的结论是①②③⑤.故选:C.
10.解:由题意得,CM=3t,BN=3t,
则BM=10﹣3t,
当∠BMN=90°时,∠B=60°,
∴∠BNM=30°,
∴BM=BN,即10﹣3t=×3t,
解得,t=,
当∠BNM=90°时,BN=BM,即10﹣3t=2×3t,
解得,t=,
综上所述,当t=或时,△BMN是一个直角三角形,故选:D.
11.解:连接OA、OB、OC,过A作AQ⊥BC于Q,
∵△ABC是边长为2的等边三角形,
∴AB=AC=BC=2,BQ=CQ==1,
由勾股定理得:AQ===,
∵S△ABC=S△ABO+S△BCO+S△ACO,
∴=++,
∴=,
∴=×2×(OE+OF+OD),
解得:OD+OE+OF=,
故答案为:.
12.解:∵△ABC为正三角形
∴∠A=∠B=∠C=60°
∵折叠
∴△ADE≌△FDE
∴∠DFE=∠A=60°
∵∠B+∠BDF+∠BFD=180°,∠DFE+∠BFD+∠CFE=180°
∴∠BDF+∠BFD=120°,∠BFD+∠CFE=120°
∴∠BDF=∠CFE
∵∠CFE+∠CEF+∠C=180°
∴∠CFE+∠CEF=120°
∴∠BDF+∠CEF=120°
故答案为:120°.
13.解:如图,∵△ABC是等边三角形,
∴∠BAC=60°,
∵∠1=42°,a∥b,
∴∠2=∠1+∠BAC=42°+60°=102°;
故答案为:102°.
14.解:①有三个角是60°的三角形是等边三角形,正确;
②有一个外角是120°的等腰三角形是等边三角形,正确;
③有一个角是60°,且是轴对称的三角形是等边三角形,正确.
④有一腰上的高也是这腰上的中线的等腰三角形是等边三角形,正确;
故答案为①②③④.
15.解;过点E作EF⊥BC,垂足为F,延长AD到H,交BC于点H,过点D作DG⊥EF,垂足为G.
∵EF⊥BC,∠EBF=60°,
∴∠BEF=30°,
∴BF=,
∵∠BED=60°,∠BEF=30°,
∴∠DEG=30°.
又∵DG⊥EF,
∴GD=,
∵AB=AC,AD平分∠BAC,
∴AH⊥BC,且BH=CH.
∵AH⊥BC,EF⊥BC,DG⊥EF,
∴四边形DGFH是矩形.
∴FH=GD=1.5.
∴BC=2BH=2×(4.5+1.5)=12.
解法二:延长ED交BC于M,证明△BEM是等边三角形,推出BM=BE=9cm,证明HM=3cm可得结论.
故答案为:12.
16.解:∵DE=CE
∴∠EDC=∠C,
∵∠EDC=∠BAC,
∴∠EDC=∠BAC=∠C,
∵∠B=60°,
∴△ABC及△DCE是等边三角形,
∵D为BC中点,
∴DE是△ABC的中位线,
∴AE:AB=1:2.
故答案为:1:2.
17.解:如图,
①连接OB,
∵AB=AC,BD=CD,
∴AD是BC垂直平分线,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DBO=∠DCO,
∵∠ABO+∠DBO=30°,
∴∠APO+∠DCO=30°.故①正确;
②∵△OBP中,∠BOP=180°﹣∠OPB﹣∠OBP,
△BOC中,∠BOC=180°﹣∠OBC﹣∠OCB,
∴∠POC=360°﹣∠BOP﹣∠BOC=∠OPB+∠OBP+∠OBC+∠OCB,
∵∠OPB=∠OBP,∠OBC=∠OCB,
∴∠POC=2∠ABD=60°,
∵PO=OC,
∴△OPC是等边三角形,故②正确;
③在AB上找到Q点使得AQ=OA,则△AOQ为等边三角形,
则∠BQO=∠PAO=120°,
在△BQO和△PAO中,
,
∴△BQO≌△PAO(AAS),
∴PA=BQ,
∵AB=BQ+AQ,
∴AC=AO+AP,故③正确;
④作CH⊥BP,
∵∠HCB=60°,∠PCO=60°,
∴∠PCH=∠OCD,
在△CDO和△CHP中,
,
∴△CDO≌△CHP(AAS),
∴S△OCD=S△CHP
∴CH=CD,
∵CD=BD,
∴BD=CH,
在Rt△ABD和Rt△ACH中,
,
∴Rt△ABD≌Rt△ACH(HL),
∴S△ABD=S△AHC,
∵四边形OAPC面积=S△OAC+S△AHC+S△CHP,S△ABC=S△AOC+S△ABD+S△OCD
∴四边形OAPC面积=S△ABC.故④错误.
故答案为:①②③.
18.解:如图延长AB到E使BE=AD,连接CE,
∴AE=AD+DB+BE=2AD+BD,
∵AC=2AD+BD,
∴AE=AC,∵∠A=60°,
∴△AEC是等边三角形,
∴∠E=∠ACE=60°,
∵∠B=4∠ACD,
设∠ACD=x,则∠ABC=4x,
在△ADC与△EBC中,,
∴△ADC≌△EBC,
∠ACD=∠ECB=x,
∴∠ABC=∠E+∠BCE,
∴4x=60°+x,∴x=20°,
∴∠BCD=60°﹣20°﹣20°=20°,
故答案为:20°
19.证明:如图,连接DE,
∵AD是BC边上的高线,CE是AB边上的中线,
∴DE=AB=AE=CD,
∵DG⊥CE于G,
由“等腰三角形三线合一”知,CG=EG.
20.证明:∵AB=AC,
∴∠ABC=∠SCB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵CE=CD,
∴∠CDE=∠E,
∵∠ACB=∠E+∠CDE=2∠DBC,
∴∠DBC=∠E,
∴△BDE为等腰三角形,BD=ED,
∵DH垂直于BE,
∴H为BE中点(三线合一).
21.证明:(1)∵△ADC≌△BOC,
∴CO=CD,
∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴∠DCO=60°,
∴△COD是等边三角形.
(2)解:AD∥OC,
理由是:∵△DOC是等边三角形,
∴∠CDO=∠DOC=60°,
∵∠α=120°,△COB≌△CDA,
∴∠ADC=∠COB=120°,
∴∠ADO=120°﹣60°=60°,
∴∠ADO=∠DOC=60°,
∴AD∥OC.
(3)解:∠AOD=360°﹣∠AOB﹣∠α﹣∠COD=360°﹣110°﹣∠α﹣60°=190°﹣∠α,
∠ADO=∠ADC﹣∠CDO=∠α﹣60°,
∠OAD=180°﹣∠AOD﹣∠ADO=180°﹣(∠α﹣60°)﹣(190°﹣∠α)=50°,
若∠ADO=∠AOD,即∠α﹣60°=190°﹣∠α,
解得:∠α=125°;
若∠ADO=∠OAD,则∠α﹣60°=50°,
解得:∠α=110°;
若∠OAD=∠AOD,即50°=190°﹣∠α,
解得:∠α=140°;
即当a为125°或110°或140°时,△AOD是等腰三角形.
22.解:(1)EF⊥AB.
∵△PCF和△PQE都是等边三角形,
∴PF=PC,PE=PQ,
∠EPF+∠FPQ=∠QPC+∠FPQ=60°,
∴∠EPF=∠QPC,
∴△PFE≌△PCQ;
∴∠EPF=∠QPC=90°,
∴EF⊥PF;
在Rt△ABC中,∠ACB=90°,∠A=30°,
∴∠B=60°;
又∵∠FPC=60°,
∴∠B=∠FPC,
∴PF∥AB(同位角相等,两直线平行),
∴EF⊥AB;
(2)当点P为BC延长线上任意一点时,(1)结论成立.
证明:∵△PCF和△PQE都是等边三角形,
∴PF=PC,PE=PQ,
∠EPF+∠EPC=∠QPC+∠EPC=60°,
∴∠EPF=∠QPC,
∴△PFE≌△PCQ;
∴∠EFP=∠QCP=90°,
∴EF⊥PF;
在Rt△ABC中,∠ACB=90°,∠A=30°,
∴∠B=60°;
又∵∠FPC=60°,
∴∠B=∠FPC,
∴PF∥AB(内错角相等,两直线平行),
∴EF⊥AB;
(3)要使(1)的结论依然成立,则需要添加条件是:∠CPF=∠B=∠QPE.
需要证明△PFE≌△PCQ、PF∥AB(内错角相等,两直线平行),才能证明EF⊥AB.
23.证明:(1)∵△ABC、△ADE是等边三角形,
∴AE=AD,BC=AC=AB,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即:∠BAD=∠CAE,
∴△BAD≌△CAE,
∴BD=EC,
∵BD=BC+CD=AC+CD,
∴CE=BD=AC+CD;
(2)由(1)知:△BAD≌△CAE,
∴∠ACE=∠ABD=60°,
∴∠ECD=180°﹣∠ACB﹣∠ACE=60°,
∴∠ECD=60°.
24.解:(1)设AP的长是x,则BP=2a﹣x,
∴S△APC+S△PBD=x?x+(2a﹣x)?(2a﹣x)
=x2﹣ax+a2,
当x=a时△APC与△PBD的面积之和取最小值,
故答案为:a;
(2)α的大小不会随点P的移动而变化,
理由:∵△APC是等边三角形,
∴PA=PC,∠APC=60°,
∵△BDP是等边三角形,
∴PB=PD,∠BPD=60°,
∴∠APC=∠BPD,
∴∠APD=∠CPB,
∴△APD≌△CPB,
∴∠PAD=∠PCB,
∵∠QAP+∠QAC+∠ACP=120°,
∴∠QCP+∠QAC+∠ACP=120°,
∴∠AQC=180°﹣120°=60°;
(3)此时α的大小不会发生改变,始终等于60°.
理由:∵△APC是等边三角形,
∴PA=PC,∠APC=60°,
∵△BDP是等边三角形,
∴PB=PD,∠BPD=60°,
∴∠APC=∠BPD,
∴∠APD=∠CPB,
∴△APD≌△CPB,
∴∠PAD=∠PCB,
∵∠QAP+∠QAC+∠ACP=120°,
∴∠QCP+∠QAC+∠ACP=120°,
∴∠AQC=180°﹣120°=60°.
25.解:(1)如图1,BM、NC、MN之间的数量关系 BM+NC=MN,
此时 ,
理由:∵DM=DN,∠MDN=60°,
∴△MDN是等边三角形,
∵△ABC是等边三角形,
∴∠A=60°,
∵BD=CD,∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠MBD=∠NCD=90°,
∵DM=DN,BD=CD,
∴Rt△BDM≌Rt△CDN,
∴∠BDM=∠CDN=30°,BM=CN,
∴DM=2BM,DN=2CN,
∴MN=2BM=2CN=BM+CN;
∴AM=AN,
∴△AMN是等边三角形,
∵AB=AM+BM,
∴AM:AB=2:3,
∴=;
(2)猜想:结论仍然成立,
证明:在NC的延长线上截取CM1=BM,连接DM1,
∵∠MBD=∠M1CD=90°,BD=CD,
∴△DBM≌△DCM1,
∴DM=DM1,∠MBD=∠M1CD,M1C=BM,
∵∠MDN=60°,∠BDC=120°,
∴∠M1DN=∠MDN=60°,
∴△MDN≌△M1DN,
∴MN=M1N=M1C+NC=BM+NC,
∴△AMN的周长为:AM+MN+AN=AM+BM+CN+AN=AB+AC,
∴=;
(3)证明:在CN上截取CM1=BM,连接DM1,
可证△DBM≌△DCM1,
∴DM=DM1,
可证∠M1DN=∠MDN=60°,
∴△MDN≌△M1DN,
∴MN=M1N,
∴NC﹣BM=MN.
26.(1)证明:在△ABM和△BCN中,
,
∴△ABM≌△BCN(SAS),
∴∠BAM=∠CBN,
∴∠BQM=∠BAQ+∠ABQ=∠MBQ+∠ABQ=60°.
(2)①是;②是;③否.
②的证明:如图,
在△ACM和△BAN中,
,
∴△ACM≌△BAN(SAS),
∴∠AMC=∠BNA,
∴∠NQA=∠NBC+∠BMQ=∠NBC+∠BNA=180°﹣60°=120°,
∴∠BQM=60°.
③的证明:如图,
在Rt△ABM和Rt△BCN中,
,
∴Rt△ABM≌Rt△BCN(SAS),
∴∠AMB=∠BNC.
又∵∠NBM+∠BNC=90°,
∴∠QBM+∠QMB=90°,
∴∠BQM=90°,即∠BQM≠60°.
27.解:(1)如图1,连接AP,则 S△ABC=S△ABP+S△APC
∴BC?AM=AB?PD+AC?PF
即 BC?h=AB?h1+AC?h2
又∵△ABC是等边三角形
∴BC=AB=AC,
∴h=h1+h2;
(2)点P在△ABC内时,h=h1+h2+h3,理由如下:
如图2,连接AP、BP、CP,则 S△ABC=S△ABP+S△BPC+S△ACP
∴BC?AM=AB?PD+AC?PE+BC?PF
即BC?h=AB?h1+AC?h2+BC?h3
又∵△ABC是等边三角形,
∴BC=AB=AC.
∴h=h1+h2+h3;
点P在△ABC外时,h=h1+h2﹣h3.
理由如下:如图3,连接PB,PC,PA
由三角形的面积公式得:S△ABC=S△PAB+S△PAC﹣S△PBC,
即BC?AM=AB?PD+AC?PE﹣BC?PF,
∵AB=BC=AC,
∴h1+h2﹣h3=h,
即h1+h2﹣h3=h.
1.在等边△ABC所在的平面内求一点P,使△PAB、△PBC、△PAC都是等腰三角形,具有这样性质的点P有( )
A.1个 B.4个 C.7个 D.10个
2.如图所示,△ABC是等边三角形,且BD=CE,∠1=15°,则∠2的度数为( )
A.15° B.30° C.45° D.60°
3.如图,△ABC是等边三角形,BC=BD,∠BAD=20°,则∠BCD的度数为( )
A.50° B.55° C.60° D.65°
4.下列条件不能得到等边三角形的是( )
A.有两个内角是60°的三角形 B.有一个角是60°的等腰三角形
C.腰和底相等的等腰三角形 D.有两个角相等的等腰三角形
5.如图,四边形ABCD中,CD=3,AD=5,AC的垂直平分线交AD于E,则△CDE的周长是( )
A.6 B.8 C.9 D.10
6.如图,在四边形ABCD中,∠A=∠B=60°,∠D=90°,AB=2,则CD长的取值范围是( )
A.<CD< B.CD>2 C.1<CD<2 D.0<CD<
7.如图,在正方体的两个面上画了两条对角线AB,AC,则∠BAC等于( )
A.60° B.75° C.90° D.135°
8.如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )
A.18° B.20° C.25° D.15°
9.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.其中正确的结论的个数是( )
A.2个 B.3个 C.4个 D.5个
10.如图等边三角形ABC中,AB=AC=BC=10cm,DC=4cm.点M、N都以3cm/s的速度运动,点M在线段CB上由点C向点B运动,点N在线段BA上由点B向点A运动.它们同时出发,当两点运动时间为t秒时,△BMN是一个直角三角形,则t的值( )
A. B. C.或 D.或
11.如图,点O是边长为2的等边三角形ABC内任意一点,且OD⊥AC,OE⊥AB,OF⊥BC,则OD+OE+OF= .
12.如图,在正△ABC中,点D在边AB上,点E在边AC上,将△ADE折叠,使点A落在BC边上的点F处,则∠BDF+∠CEF= .
13.如图,直线a,b过等边三角形ABC顶点A和C,且a∥b,∠1=42°,则∠2的度数为 .
14.在下列结论中:①有三个角是60°的三角形是等边三角形;②有一个外角是120°的等腰三角形是等边三角形;③有一个角是60°,且是轴对称的三角形是等边三角形;④有一腰上的高也是这腰上的中线的等腰三角形是等边三角形.其中正确的是 .
15.如图,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=9cm,DE=3cm,则BC= cm.
16.如图,在△ABC中,∠B=60°,∠EDC=∠BAC,且D为BC中点,DE=CE,则AE:AB的值为 .
17.已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形ADCP;其中正确的有 (填上所有正确结论的序号)
18.如图,已知△ABC中,∠A=60°,D为AB上一点,且AC=2AD+BD,∠B=4∠ACD,则∠DCB的度数是 .
19.已知如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.求证:CG=EG.
20.如图,在等腰△ABC中,AB=AC,BD为∠ABC平分线,延长BC到点E,使CE=CD,作DH⊥BE于H,求证:H为BE的中点.
21.如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,则△ADC≌△BOC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=120°时,试判断AD与OC的位置关系,并说明理由;
(3)探究:当a为多少度时,△AOD是等腰三角形?
22.如图1,在Rt△ABC中,∠ACB=90°,∠A=30°,P为BC边上任意一点,点Q为AC边动点,分别以CP、PQ为边做等边△PCF和等边△PQE,连接EF.
(1)试探索EF与AB位置关系,并证明;
(2)如图2,当点P为BC延长线上任意一点时,(1)结论是否成立?请说明理由.
(3)如图3,在Rt△ABC中,∠ACB=90°,∠A=m°,P为BC延长线上一点,点Q为AC边动点,分别以CP、PQ为腰做等腰△PCF和等腰△PQE,使得PC=PF,PQ=PE,连接EF.要使(1)的结论依然成立,则需要添加怎样的条件?为什么?
23.如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.
求证:(1)CE=AC+DC;(2)∠ECD=60°.
24.如图1,已知线段AB的长为2a,点P是AB上的动点(P不与A,B重合),分别以AP、PB为边向线段AB的同一侧作正△APC和正△PBD.
(1)当△APC与△PBD的面积之和取最小值时,AP= ;(直接写结果)
(2)连接AD、BC,相交于点Q,设∠AQC=α,那么α的大小是否会随点P的移动而变化?请说明理由;
(3)如图2,若点P固定,将△PBD绕点P按顺时针方向旋转(旋转角小于180°),此时α的大小是否发生变化?(只需直接写出你的猜想,不必证明)
25.在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系.
(1)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是 ;此时= ;
(2)如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想(I)问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.
(3)如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.
26.学完“几何的回顾”一章后,老师布置了一道思考题:
如图,点M,N分别在正三角形ABC的BC,CA边上,且BM=CN,AM,BN交于点Q.求证:∠BQM=60度.
(1)请你完成这道思考题;
(2)做完(1)后,同学们在老师的启发下进行了反思,提出了许多问题,如:
①若将题中“BM=CN”与“∠BQM=60°”的位置交换,得到的是否仍是真命题?
②若将题中的点M,N分别移动到BC,CA的延长线上,是否仍能得到∠BQM=60°?
③若将题中的条件“点M,N分别在正三角形ABC的BC,CA边上”改为“点M,N分别在正方形ABCD的BC,CD边上”,是否仍能得到∠BQM=60°?…
请你作出判断,在下列横线上填写“是”或“否”:① ;② ;③ .并对②,③的判断,选择一个给出证明.
27.已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC的距离分别为h1,h2,h3,△ABC的高为h.
(1)若点P在一边BC上[如图①],此时h3=0,求证:h1+h2+h3=h;
(2)当点P在△ABC内[如图②],以及点P在△ABC外[如图③]这两种情况时,上述结论是否成立?若成立,请予以证明;若不成立,h1,h2,h3与h之间又有怎样的关系,请说出你的猜想,并说明理由.
参考答案
1.解:(1)点P在三角形内部时,点P是边AB、BC、CA的垂直平分线的交点,是三角形的外心;
(2)分别以三角形各顶点为圆心,边长为半径,交垂直平分线的交点就是满足要求的.每条垂直平分线上得3个交点,再加三角形的垂心,一共10个.故具有这种性质的点P共有10个.故选:D.
2.解:在△ABD和△BCE中,
,
∴△ABD≌△BCE,
∴∠1=∠CBE,
∵∠2=∠1+∠ABE,
∴∠2=∠CBE+∠ABE=∠ABC=60°.
故选:D.
3.解:∵△ABC是等边三角形,
∴∠ABC=60°,AB=BC,
∵BC=BD,
∴AB=BD,
∴∠BAD=∠BDA=20°,
∴∠ABD=180°﹣20°﹣20°=140°,
∴∠CBD=80°,
∴∠BCD=∠BDC=(180°﹣80°)=50°,故选:A.
4.解:A、有两个内角是60°的三角形是等边三角形,不符合题意;
B、有一个角是60°的等腰三角形是等边三角形,不符合题意;
C、腰和底相等的等腰三角形是等边三角形,不符合题意;
D、有两个角相等的等腰三角形可能不是等边三角形,符合题意;故选:D.
5.解:∵AC的垂直平分线交AD于E,
∴AE=CE,
∴△CDE的周长是:DE+CD+CE=DC+DE+AE=DC+AD=3+5=8.
故选:B.
6.解:延长AD,BC交于E,
∵∠A=∠B=60°,
∴△ABE是等边三角形,
过B作BF⊥AE于F,
∵AB=2,
∴BF=,
∵∠D=90°,
∴CD∥BF,
∴CD长的取值范围是0<CD<,故选:D.
7.解:连接BC,如图,
∵AB、AC和BC都是正方体的三个面的对角线,
∴AB=AC=BC,
∴△ABC为等边三角形,
∴∠BAC=60°.故选:A.
8.解:如图延长BD到M使得DM=DC,
∵∠ADB=78°,
∴∠ADM=180°﹣∠ADB=102°,
∵∠ADB=78°,∠BDC=24°,
∴∠ADC=∠ADB+∠BDC=102°,
∴∠ADM=∠ADC,
在△ADM和△ADC中,
,
∴△ADM≌△ADC,
∴AM=AC=AB,
∵∠ABD=60°,
∴△AMB是等边三角形,
∴∠M=∠DCA=60°,
∵∠DOC=∠AOB,∠DCO=∠ABO=60°,
∴∠BAO=∠ODC=24°,
∵∠CAB+∠ABC+∠ACB=180°,
∴24°+2(60°+∠CBD)=180°,
∴∠CBD=18°,故选:A.
9.解:①△ABC和△DCE均是等边三角形,点A,C,E在同一条直线上,
∴AC=BC,EC=DC,∠BCE=∠ACD=120°
∴△ACD≌△ECB
∴AD=BE,故本选项正确;
②∵△ACD≌△ECB
∴∠CBQ=∠CAP,
又∵∠PCQ=∠ACB=60°,CB=AC,
∴△BCQ≌△ACP,
∴CQ=CP,又∠PCQ=60°,
∴△PCQ为等边三角形,
∴∠QPC=60°=∠ACB,
∴PQ∥AE,故本选项正确;
③∵∠ACB=∠DCE=60°,
∴∠BCD=60°,
∴∠ACP=∠BCQ,
∵AC=BC,∠DAC=∠QBC,
∴△ACP≌△BCQ(ASA),
∴CP=CQ,AP=BQ,故本选项正确;
④已知△ABC、△DCE为正三角形,
故∠DCE=∠BCA=60°?∠DCB=60°,
又因为∠DPC=∠DAC+∠BCA,∠BCA=60°?∠DPC>60°,
故DP不等于DE,故本选项错误;
⑤∵△ABC、△DCE为正三角形,
∴∠ACB=∠DCE=60°,AC=BC,DC=EC,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
∴∠AOB=∠CAD+∠CEB=∠CBE+∠CEB,
∵∠ACB=∠CBE+∠CEB=60°,
∴∠AOB=60°,
故本选项正确.
综上所述,正确的结论是①②③⑤.故选:C.
10.解:由题意得,CM=3t,BN=3t,
则BM=10﹣3t,
当∠BMN=90°时,∠B=60°,
∴∠BNM=30°,
∴BM=BN,即10﹣3t=×3t,
解得,t=,
当∠BNM=90°时,BN=BM,即10﹣3t=2×3t,
解得,t=,
综上所述,当t=或时,△BMN是一个直角三角形,故选:D.
11.解:连接OA、OB、OC,过A作AQ⊥BC于Q,
∵△ABC是边长为2的等边三角形,
∴AB=AC=BC=2,BQ=CQ==1,
由勾股定理得:AQ===,
∵S△ABC=S△ABO+S△BCO+S△ACO,
∴=++,
∴=,
∴=×2×(OE+OF+OD),
解得:OD+OE+OF=,
故答案为:.
12.解:∵△ABC为正三角形
∴∠A=∠B=∠C=60°
∵折叠
∴△ADE≌△FDE
∴∠DFE=∠A=60°
∵∠B+∠BDF+∠BFD=180°,∠DFE+∠BFD+∠CFE=180°
∴∠BDF+∠BFD=120°,∠BFD+∠CFE=120°
∴∠BDF=∠CFE
∵∠CFE+∠CEF+∠C=180°
∴∠CFE+∠CEF=120°
∴∠BDF+∠CEF=120°
故答案为:120°.
13.解:如图,∵△ABC是等边三角形,
∴∠BAC=60°,
∵∠1=42°,a∥b,
∴∠2=∠1+∠BAC=42°+60°=102°;
故答案为:102°.
14.解:①有三个角是60°的三角形是等边三角形,正确;
②有一个外角是120°的等腰三角形是等边三角形,正确;
③有一个角是60°,且是轴对称的三角形是等边三角形,正确.
④有一腰上的高也是这腰上的中线的等腰三角形是等边三角形,正确;
故答案为①②③④.
15.解;过点E作EF⊥BC,垂足为F,延长AD到H,交BC于点H,过点D作DG⊥EF,垂足为G.
∵EF⊥BC,∠EBF=60°,
∴∠BEF=30°,
∴BF=,
∵∠BED=60°,∠BEF=30°,
∴∠DEG=30°.
又∵DG⊥EF,
∴GD=,
∵AB=AC,AD平分∠BAC,
∴AH⊥BC,且BH=CH.
∵AH⊥BC,EF⊥BC,DG⊥EF,
∴四边形DGFH是矩形.
∴FH=GD=1.5.
∴BC=2BH=2×(4.5+1.5)=12.
解法二:延长ED交BC于M,证明△BEM是等边三角形,推出BM=BE=9cm,证明HM=3cm可得结论.
故答案为:12.
16.解:∵DE=CE
∴∠EDC=∠C,
∵∠EDC=∠BAC,
∴∠EDC=∠BAC=∠C,
∵∠B=60°,
∴△ABC及△DCE是等边三角形,
∵D为BC中点,
∴DE是△ABC的中位线,
∴AE:AB=1:2.
故答案为:1:2.
17.解:如图,
①连接OB,
∵AB=AC,BD=CD,
∴AD是BC垂直平分线,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DBO=∠DCO,
∵∠ABO+∠DBO=30°,
∴∠APO+∠DCO=30°.故①正确;
②∵△OBP中,∠BOP=180°﹣∠OPB﹣∠OBP,
△BOC中,∠BOC=180°﹣∠OBC﹣∠OCB,
∴∠POC=360°﹣∠BOP﹣∠BOC=∠OPB+∠OBP+∠OBC+∠OCB,
∵∠OPB=∠OBP,∠OBC=∠OCB,
∴∠POC=2∠ABD=60°,
∵PO=OC,
∴△OPC是等边三角形,故②正确;
③在AB上找到Q点使得AQ=OA,则△AOQ为等边三角形,
则∠BQO=∠PAO=120°,
在△BQO和△PAO中,
,
∴△BQO≌△PAO(AAS),
∴PA=BQ,
∵AB=BQ+AQ,
∴AC=AO+AP,故③正确;
④作CH⊥BP,
∵∠HCB=60°,∠PCO=60°,
∴∠PCH=∠OCD,
在△CDO和△CHP中,
,
∴△CDO≌△CHP(AAS),
∴S△OCD=S△CHP
∴CH=CD,
∵CD=BD,
∴BD=CH,
在Rt△ABD和Rt△ACH中,
,
∴Rt△ABD≌Rt△ACH(HL),
∴S△ABD=S△AHC,
∵四边形OAPC面积=S△OAC+S△AHC+S△CHP,S△ABC=S△AOC+S△ABD+S△OCD
∴四边形OAPC面积=S△ABC.故④错误.
故答案为:①②③.
18.解:如图延长AB到E使BE=AD,连接CE,
∴AE=AD+DB+BE=2AD+BD,
∵AC=2AD+BD,
∴AE=AC,∵∠A=60°,
∴△AEC是等边三角形,
∴∠E=∠ACE=60°,
∵∠B=4∠ACD,
设∠ACD=x,则∠ABC=4x,
在△ADC与△EBC中,,
∴△ADC≌△EBC,
∠ACD=∠ECB=x,
∴∠ABC=∠E+∠BCE,
∴4x=60°+x,∴x=20°,
∴∠BCD=60°﹣20°﹣20°=20°,
故答案为:20°
19.证明:如图,连接DE,
∵AD是BC边上的高线,CE是AB边上的中线,
∴DE=AB=AE=CD,
∵DG⊥CE于G,
由“等腰三角形三线合一”知,CG=EG.
20.证明:∵AB=AC,
∴∠ABC=∠SCB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵CE=CD,
∴∠CDE=∠E,
∵∠ACB=∠E+∠CDE=2∠DBC,
∴∠DBC=∠E,
∴△BDE为等腰三角形,BD=ED,
∵DH垂直于BE,
∴H为BE中点(三线合一).
21.证明:(1)∵△ADC≌△BOC,
∴CO=CD,
∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴∠DCO=60°,
∴△COD是等边三角形.
(2)解:AD∥OC,
理由是:∵△DOC是等边三角形,
∴∠CDO=∠DOC=60°,
∵∠α=120°,△COB≌△CDA,
∴∠ADC=∠COB=120°,
∴∠ADO=120°﹣60°=60°,
∴∠ADO=∠DOC=60°,
∴AD∥OC.
(3)解:∠AOD=360°﹣∠AOB﹣∠α﹣∠COD=360°﹣110°﹣∠α﹣60°=190°﹣∠α,
∠ADO=∠ADC﹣∠CDO=∠α﹣60°,
∠OAD=180°﹣∠AOD﹣∠ADO=180°﹣(∠α﹣60°)﹣(190°﹣∠α)=50°,
若∠ADO=∠AOD,即∠α﹣60°=190°﹣∠α,
解得:∠α=125°;
若∠ADO=∠OAD,则∠α﹣60°=50°,
解得:∠α=110°;
若∠OAD=∠AOD,即50°=190°﹣∠α,
解得:∠α=140°;
即当a为125°或110°或140°时,△AOD是等腰三角形.
22.解:(1)EF⊥AB.
∵△PCF和△PQE都是等边三角形,
∴PF=PC,PE=PQ,
∠EPF+∠FPQ=∠QPC+∠FPQ=60°,
∴∠EPF=∠QPC,
∴△PFE≌△PCQ;
∴∠EPF=∠QPC=90°,
∴EF⊥PF;
在Rt△ABC中,∠ACB=90°,∠A=30°,
∴∠B=60°;
又∵∠FPC=60°,
∴∠B=∠FPC,
∴PF∥AB(同位角相等,两直线平行),
∴EF⊥AB;
(2)当点P为BC延长线上任意一点时,(1)结论成立.
证明:∵△PCF和△PQE都是等边三角形,
∴PF=PC,PE=PQ,
∠EPF+∠EPC=∠QPC+∠EPC=60°,
∴∠EPF=∠QPC,
∴△PFE≌△PCQ;
∴∠EFP=∠QCP=90°,
∴EF⊥PF;
在Rt△ABC中,∠ACB=90°,∠A=30°,
∴∠B=60°;
又∵∠FPC=60°,
∴∠B=∠FPC,
∴PF∥AB(内错角相等,两直线平行),
∴EF⊥AB;
(3)要使(1)的结论依然成立,则需要添加条件是:∠CPF=∠B=∠QPE.
需要证明△PFE≌△PCQ、PF∥AB(内错角相等,两直线平行),才能证明EF⊥AB.
23.证明:(1)∵△ABC、△ADE是等边三角形,
∴AE=AD,BC=AC=AB,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即:∠BAD=∠CAE,
∴△BAD≌△CAE,
∴BD=EC,
∵BD=BC+CD=AC+CD,
∴CE=BD=AC+CD;
(2)由(1)知:△BAD≌△CAE,
∴∠ACE=∠ABD=60°,
∴∠ECD=180°﹣∠ACB﹣∠ACE=60°,
∴∠ECD=60°.
24.解:(1)设AP的长是x,则BP=2a﹣x,
∴S△APC+S△PBD=x?x+(2a﹣x)?(2a﹣x)
=x2﹣ax+a2,
当x=a时△APC与△PBD的面积之和取最小值,
故答案为:a;
(2)α的大小不会随点P的移动而变化,
理由:∵△APC是等边三角形,
∴PA=PC,∠APC=60°,
∵△BDP是等边三角形,
∴PB=PD,∠BPD=60°,
∴∠APC=∠BPD,
∴∠APD=∠CPB,
∴△APD≌△CPB,
∴∠PAD=∠PCB,
∵∠QAP+∠QAC+∠ACP=120°,
∴∠QCP+∠QAC+∠ACP=120°,
∴∠AQC=180°﹣120°=60°;
(3)此时α的大小不会发生改变,始终等于60°.
理由:∵△APC是等边三角形,
∴PA=PC,∠APC=60°,
∵△BDP是等边三角形,
∴PB=PD,∠BPD=60°,
∴∠APC=∠BPD,
∴∠APD=∠CPB,
∴△APD≌△CPB,
∴∠PAD=∠PCB,
∵∠QAP+∠QAC+∠ACP=120°,
∴∠QCP+∠QAC+∠ACP=120°,
∴∠AQC=180°﹣120°=60°.
25.解:(1)如图1,BM、NC、MN之间的数量关系 BM+NC=MN,
此时 ,
理由:∵DM=DN,∠MDN=60°,
∴△MDN是等边三角形,
∵△ABC是等边三角形,
∴∠A=60°,
∵BD=CD,∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠MBD=∠NCD=90°,
∵DM=DN,BD=CD,
∴Rt△BDM≌Rt△CDN,
∴∠BDM=∠CDN=30°,BM=CN,
∴DM=2BM,DN=2CN,
∴MN=2BM=2CN=BM+CN;
∴AM=AN,
∴△AMN是等边三角形,
∵AB=AM+BM,
∴AM:AB=2:3,
∴=;
(2)猜想:结论仍然成立,
证明:在NC的延长线上截取CM1=BM,连接DM1,
∵∠MBD=∠M1CD=90°,BD=CD,
∴△DBM≌△DCM1,
∴DM=DM1,∠MBD=∠M1CD,M1C=BM,
∵∠MDN=60°,∠BDC=120°,
∴∠M1DN=∠MDN=60°,
∴△MDN≌△M1DN,
∴MN=M1N=M1C+NC=BM+NC,
∴△AMN的周长为:AM+MN+AN=AM+BM+CN+AN=AB+AC,
∴=;
(3)证明:在CN上截取CM1=BM,连接DM1,
可证△DBM≌△DCM1,
∴DM=DM1,
可证∠M1DN=∠MDN=60°,
∴△MDN≌△M1DN,
∴MN=M1N,
∴NC﹣BM=MN.
26.(1)证明:在△ABM和△BCN中,
,
∴△ABM≌△BCN(SAS),
∴∠BAM=∠CBN,
∴∠BQM=∠BAQ+∠ABQ=∠MBQ+∠ABQ=60°.
(2)①是;②是;③否.
②的证明:如图,
在△ACM和△BAN中,
,
∴△ACM≌△BAN(SAS),
∴∠AMC=∠BNA,
∴∠NQA=∠NBC+∠BMQ=∠NBC+∠BNA=180°﹣60°=120°,
∴∠BQM=60°.
③的证明:如图,
在Rt△ABM和Rt△BCN中,
,
∴Rt△ABM≌Rt△BCN(SAS),
∴∠AMB=∠BNC.
又∵∠NBM+∠BNC=90°,
∴∠QBM+∠QMB=90°,
∴∠BQM=90°,即∠BQM≠60°.
27.解:(1)如图1,连接AP,则 S△ABC=S△ABP+S△APC
∴BC?AM=AB?PD+AC?PF
即 BC?h=AB?h1+AC?h2
又∵△ABC是等边三角形
∴BC=AB=AC,
∴h=h1+h2;
(2)点P在△ABC内时,h=h1+h2+h3,理由如下:
如图2,连接AP、BP、CP,则 S△ABC=S△ABP+S△BPC+S△ACP
∴BC?AM=AB?PD+AC?PE+BC?PF
即BC?h=AB?h1+AC?h2+BC?h3
又∵△ABC是等边三角形,
∴BC=AB=AC.
∴h=h1+h2+h3;
点P在△ABC外时,h=h1+h2﹣h3.
理由如下:如图3,连接PB,PC,PA
由三角形的面积公式得:S△ABC=S△PAB+S△PAC﹣S△PBC,
即BC?AM=AB?PD+AC?PE﹣BC?PF,
∵AB=BC=AC,
∴h1+h2﹣h3=h,
即h1+h2﹣h3=h.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
