华东师大版九年级数学上册 22.2.1一元二次方程的解法——直接开平方法和因式分解法同步练习(word版含答案)
文档属性
| 名称 | 华东师大版九年级数学上册 22.2.1一元二次方程的解法——直接开平方法和因式分解法同步练习(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 387.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 00:00:00 | ||
图片预览




文档简介
22.2.1一元二次方程的解法——直接开平方法和因式分解法
一、单选题
1.方程的解为(
)
A.或
B.或
C.
D.
2.一元二次方程x2﹣9=0的两根分别是a,b,且a>b,则2a﹣b的值为(
)
A.3
B.﹣3
C.6
D.9
3.一元二次方程x2+2x=0的解是( )
A.x1=x2=﹣2
B.x1=2,x2=0
C.x1=﹣2,x2=0
D.x1=2,x2=﹣2
4.关于x的一元二次方程有一个根是0,则k的值是(
)
A.0
B.1
C.-2
D.1或-2
5.解一元二次方程的过程中,变形正确的为(
)
A.
B.
C.
D.
6.一个等腰三角形的底边长是6,腰长是一元二次方程的一个根,则此三角形的周长是(
).
A.12
B.14
C.12或14
D.9或12
7.若一元二次方程(x﹣2)2=9可转化为两个一元一次方程,一个一元一次方程是x﹣2=3,则另一个一元一次方程是( )
A.x﹣2=3
B.x﹣2=﹣3
C.x+2=3
D.x+2=﹣3
8.已知关于的一元二次方程有一个根为,则的值为(
)
A.
B.
C.
D.
9.关于的方程能直接开平方求解的条件是(
)
A.
B.
C.为任意数
D.为任意数且
10.已知一个菱形的边长是,两条对角线长的比是4:3,则这个菱形的面积是(
)
A.
B.
C.
D.
11.若实数k、b是一元二次方程的两个根,且,则一次函数的图象不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
12.将4个数a,b,c,d排成2行,2列,两边各加一条竖直线记成,定义,上述记号就叫做2阶行列式.若,则x的值为(
)
A.±2
B.
C.±4
D.2
二、填空题
13.已知三角形两边的长分别是8和6,第三边的长是一元二次方程的一个实数根,则该三角形的周长是_______.
14.一元二次方程x2+9x=0的较大的根为_____.
15.已知,那的值是________
16.如果是一元二次方程的一个根,则常数的值是__________.
17.关于x的方程(k+1)x2+(k+3)x+2=0的根为整数,则所有整数的和为____________.
三、解答题
18.解下列一元二次方程:
(1)
(2)
(3)
(4)
19.已知两个整式,.
(1)若的值是1,求和的值;
(2)若的值是0,求的值.
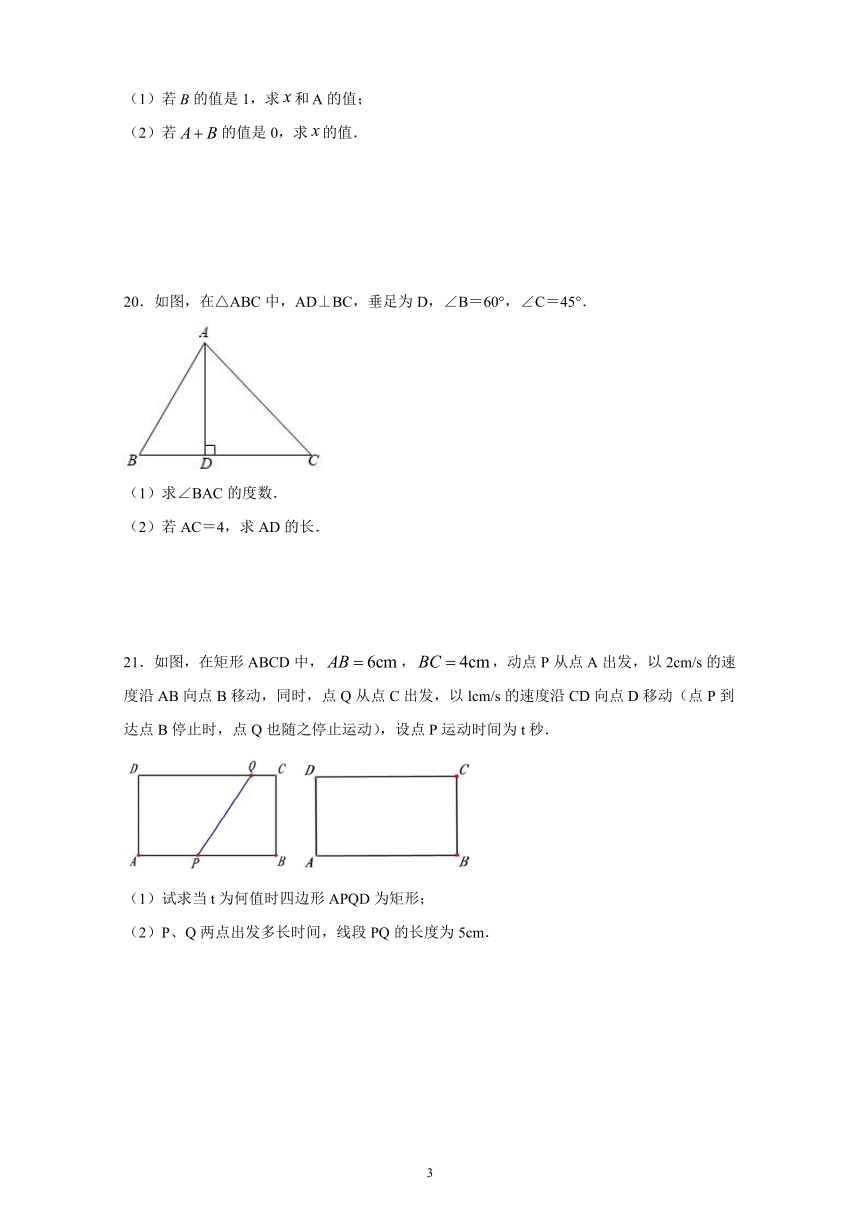
20.如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
(1)求∠BAC的度数.
(2)若AC=4,求AD的长.
21.如图,在矩形ABCD中,,,动点P从点A出发,以2cm/s的速度沿AB向点B移动,同时,点Q从点C出发,以lcm/s的速度沿CD向点D移动(点P到达点B停止时,点Q也随之停止运动),设点P运动时间为t秒.
(1)试求当t为何值时四边形APQD为矩形;
(2)P、Q两点出发多长时间,线段PQ的长度为5cm.
参考答案
1.B
解:,
开方,得x-3=±1,
解得:x=4或x=2,
故选:B.
2.D
解:解方程x2﹣9=0得a=3,b=﹣3,
所以2a﹣b=2×3﹣(﹣3)=9.
故选:D.
3.C
解:x2+2x=0,
x(x+2)=0,
x+2=0或x=0,
解得:x1=﹣2,x2=0,
故选择:C.
4.C
解:∵x的一元二次方程有一个根是0,
∴,且k-1≠0,
解得k=
-2或k=1,且k≠1,
∴k=
-2,
故选C.
5.B
解:
;
故选B.
6.B
解方程,
用因式分解法整理为:,
得,
则等腰三角形的三边为4,4,6或3,3,6(舍去),
∴等腰三角形的周长为4+4+6=14,
故选:B.
7.B
解:∵(x-2)2=9,
∴x-2=3,x-2=-3,
即另一个方程是x-2=-3,
故选:B.
8.C
解:将代入关于的一元二次方程得,
故选:C.
9.D
解:∵,
∴,为任意数,
故选:D.
10.B
解:设菱形的对角线分别为和,
菱形的面积,
已知菱形菱形的边长为,
根据菱形的性质可知,菱形的对角线互相垂直平分,即可知,
解得,
所以菱形的面积,
故选:B.
11.C
∵实数k、b是一元二次方程的两个根,且,
∴,
∴一次函数表达式为,
有图像可知,一次函数不经过第三象限.
故选:C.
12.A
解:由题意可得:,
则(x+1)2-2(x-1)=7,
解得:x=±2.
故选:A.
13.20
解:x2-12x+36=0,
因式分解得:(x-6)2=0,
解得:x1=x2=6,
当x=6时,三角形三边长为6,6,8,
则周长为20.
故答案为:20.
14.0
解:∵一元二次方程x2+9x=0,即,
∴解得:x1=0,x2=9,
∴此方程较大根是0,
故答案为:0.
15.
解:
或
或
经检验:不合题意,舍去,
故答案为:
16.
解:把代入得:8-4=a2,解得a=.
故答案为:.
17.
解:当时,原方程可化为
解得为整数;
当时,原方程是关于x的一元二次方程,可化为
根据题意根为整数,或,
解得
所有整数的和为:
故答案为:-5.
18.(1);
(2);(3);(4)
解:(1)x2-16=0,
x2=16,
x=±4,
即x1=4,x2=-4;
(2)x2-3x=0,
x(x-3)=0,
x=0或x-3=0,
解得:x1=0,x2=3;
(3)x2-4x-5=0,
(x-5)(x+1)=0,
x-5=0或x+1=0,
解得:x1=5,x2=-1;
(4)3x2+5x-2=0,
(3x-1)(x+2)=0,
3x-1=0,x+2=0,
解得:.
19.(1),A=-1;(2)或
解:(1)∵的值是1,∴,
∴;
∴;
(2)∵的值是0,
∴,
即,
,∴或.
20.(1)∠BAC=75°;(2)AD的长为.
解:(1)∵在△ABC中,∠B=60°,∠C=45°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣60°﹣45°=75°;
(2)∵AD⊥BC,∠C=45°,
∴∠CAD=45°=∠C,
∴AD=CD,
设AD=CD=x,由勾股定理得AD2+CD2=AC2,
即x2+x2=42,解得x=,
即AD的长为.
21.(1)2;(2)当出发1s或3s时,线段PQ的长度为5cm.
解:(1)四边形APQD为矩形.
,
,
,
,
当时四边形APQD为矩形;
(2)过点P作于点E,
,
四边形APED是矩形.
,
,
在中,,
,,,
答:当出发1s或3s时,线段PQ的长度为5cm.
一、单选题
1.方程的解为(
)
A.或
B.或
C.
D.
2.一元二次方程x2﹣9=0的两根分别是a,b,且a>b,则2a﹣b的值为(
)
A.3
B.﹣3
C.6
D.9
3.一元二次方程x2+2x=0的解是( )
A.x1=x2=﹣2
B.x1=2,x2=0
C.x1=﹣2,x2=0
D.x1=2,x2=﹣2
4.关于x的一元二次方程有一个根是0,则k的值是(
)
A.0
B.1
C.-2
D.1或-2
5.解一元二次方程的过程中,变形正确的为(
)
A.
B.
C.
D.
6.一个等腰三角形的底边长是6,腰长是一元二次方程的一个根,则此三角形的周长是(
).
A.12
B.14
C.12或14
D.9或12
7.若一元二次方程(x﹣2)2=9可转化为两个一元一次方程,一个一元一次方程是x﹣2=3,则另一个一元一次方程是( )
A.x﹣2=3
B.x﹣2=﹣3
C.x+2=3
D.x+2=﹣3
8.已知关于的一元二次方程有一个根为,则的值为(
)
A.
B.
C.
D.
9.关于的方程能直接开平方求解的条件是(
)
A.
B.
C.为任意数
D.为任意数且
10.已知一个菱形的边长是,两条对角线长的比是4:3,则这个菱形的面积是(
)
A.
B.
C.
D.
11.若实数k、b是一元二次方程的两个根,且,则一次函数的图象不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
12.将4个数a,b,c,d排成2行,2列,两边各加一条竖直线记成,定义,上述记号就叫做2阶行列式.若,则x的值为(
)
A.±2
B.
C.±4
D.2
二、填空题
13.已知三角形两边的长分别是8和6,第三边的长是一元二次方程的一个实数根,则该三角形的周长是_______.
14.一元二次方程x2+9x=0的较大的根为_____.
15.已知,那的值是________
16.如果是一元二次方程的一个根,则常数的值是__________.
17.关于x的方程(k+1)x2+(k+3)x+2=0的根为整数,则所有整数的和为____________.
三、解答题
18.解下列一元二次方程:
(1)
(2)
(3)
(4)
19.已知两个整式,.
(1)若的值是1,求和的值;
(2)若的值是0,求的值.
20.如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
(1)求∠BAC的度数.
(2)若AC=4,求AD的长.
21.如图,在矩形ABCD中,,,动点P从点A出发,以2cm/s的速度沿AB向点B移动,同时,点Q从点C出发,以lcm/s的速度沿CD向点D移动(点P到达点B停止时,点Q也随之停止运动),设点P运动时间为t秒.
(1)试求当t为何值时四边形APQD为矩形;
(2)P、Q两点出发多长时间,线段PQ的长度为5cm.
参考答案
1.B
解:,
开方,得x-3=±1,
解得:x=4或x=2,
故选:B.
2.D
解:解方程x2﹣9=0得a=3,b=﹣3,
所以2a﹣b=2×3﹣(﹣3)=9.
故选:D.
3.C
解:x2+2x=0,
x(x+2)=0,
x+2=0或x=0,
解得:x1=﹣2,x2=0,
故选择:C.
4.C
解:∵x的一元二次方程有一个根是0,
∴,且k-1≠0,
解得k=
-2或k=1,且k≠1,
∴k=
-2,
故选C.
5.B
解:
;
故选B.
6.B
解方程,
用因式分解法整理为:,
得,
则等腰三角形的三边为4,4,6或3,3,6(舍去),
∴等腰三角形的周长为4+4+6=14,
故选:B.
7.B
解:∵(x-2)2=9,
∴x-2=3,x-2=-3,
即另一个方程是x-2=-3,
故选:B.
8.C
解:将代入关于的一元二次方程得,
故选:C.
9.D
解:∵,
∴,为任意数,
故选:D.
10.B
解:设菱形的对角线分别为和,
菱形的面积,
已知菱形菱形的边长为,
根据菱形的性质可知,菱形的对角线互相垂直平分,即可知,
解得,
所以菱形的面积,
故选:B.
11.C
∵实数k、b是一元二次方程的两个根,且,
∴,
∴一次函数表达式为,
有图像可知,一次函数不经过第三象限.
故选:C.
12.A
解:由题意可得:,
则(x+1)2-2(x-1)=7,
解得:x=±2.
故选:A.
13.20
解:x2-12x+36=0,
因式分解得:(x-6)2=0,
解得:x1=x2=6,
当x=6时,三角形三边长为6,6,8,
则周长为20.
故答案为:20.
14.0
解:∵一元二次方程x2+9x=0,即,
∴解得:x1=0,x2=9,
∴此方程较大根是0,
故答案为:0.
15.
解:
或
或
经检验:不合题意,舍去,
故答案为:
16.
解:把代入得:8-4=a2,解得a=.
故答案为:.
17.
解:当时,原方程可化为
解得为整数;
当时,原方程是关于x的一元二次方程,可化为
根据题意根为整数,或,
解得
所有整数的和为:
故答案为:-5.
18.(1);
(2);(3);(4)
解:(1)x2-16=0,
x2=16,
x=±4,
即x1=4,x2=-4;
(2)x2-3x=0,
x(x-3)=0,
x=0或x-3=0,
解得:x1=0,x2=3;
(3)x2-4x-5=0,
(x-5)(x+1)=0,
x-5=0或x+1=0,
解得:x1=5,x2=-1;
(4)3x2+5x-2=0,
(3x-1)(x+2)=0,
3x-1=0,x+2=0,
解得:.
19.(1),A=-1;(2)或
解:(1)∵的值是1,∴,
∴;
∴;
(2)∵的值是0,
∴,
即,
,∴或.
20.(1)∠BAC=75°;(2)AD的长为.
解:(1)∵在△ABC中,∠B=60°,∠C=45°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣60°﹣45°=75°;
(2)∵AD⊥BC,∠C=45°,
∴∠CAD=45°=∠C,
∴AD=CD,
设AD=CD=x,由勾股定理得AD2+CD2=AC2,
即x2+x2=42,解得x=,
即AD的长为.
21.(1)2;(2)当出发1s或3s时,线段PQ的长度为5cm.
解:(1)四边形APQD为矩形.
,
,
,
,
当时四边形APQD为矩形;
(2)过点P作于点E,
,
四边形APED是矩形.
,
,
在中,,
,,,
答:当出发1s或3s时,线段PQ的长度为5cm.
