2021-2022学年北师大版九年级数学上册1.3正方形的性质与判定同步优生辅导训练(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册1.3正方形的性质与判定同步优生辅导训练(Word版,附答案解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 495.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 00:00:00 | ||
图片预览


文档简介
2021年北师大版九年级数学上册《1.3正方形的性质与判定》同步优生辅导训练(附答案)
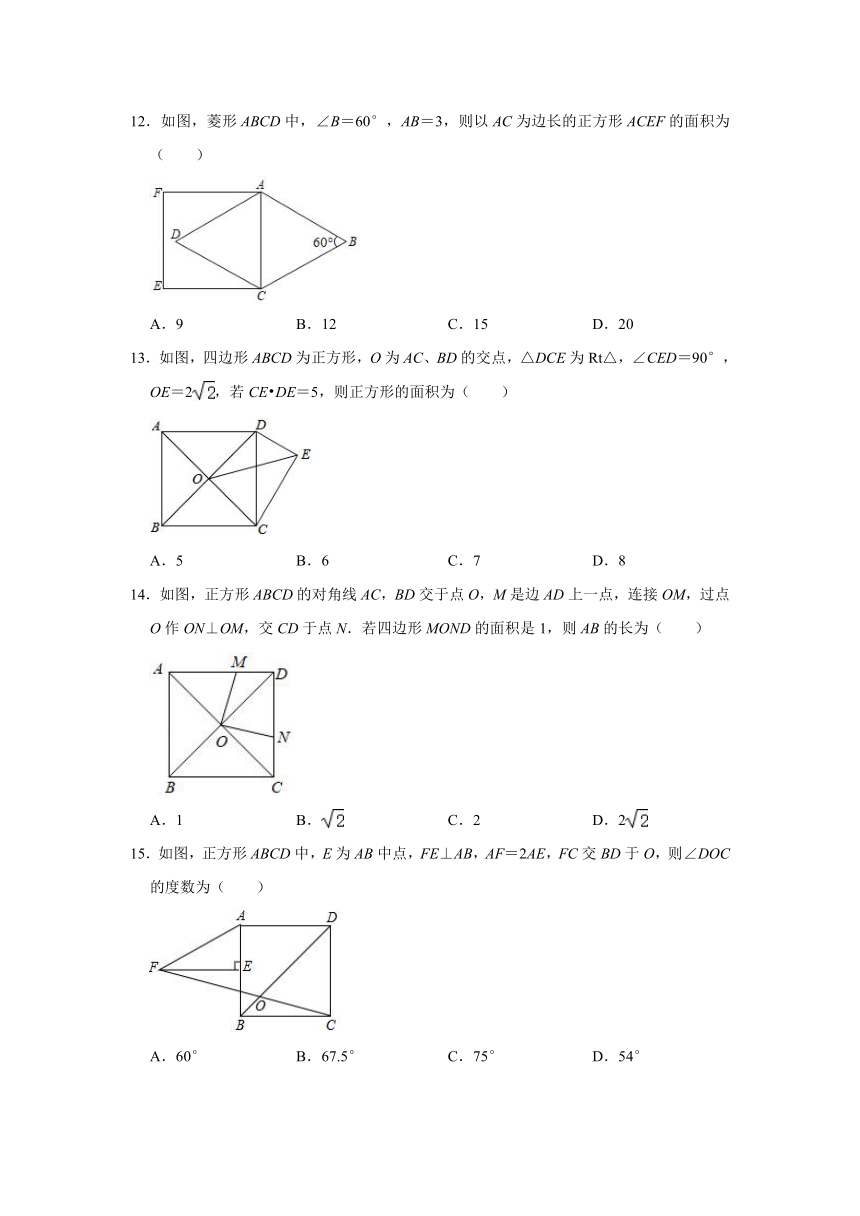
1.下列说法判断错误的是( )
A.对角线相互平分的四边形是平行四边形 B.对角线相等的四边形是矩形
C.对角线相互垂直平分的四边形是菱形D.对角线相互垂直且相等的平行四边形是正方形
2.如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E(2,3),则点F的坐标为( )
A.(﹣1,5) B.(﹣2,3) C.(5,﹣1) D.(﹣3,2)
3.如图,在正方形ABCD中,AB=1,P为其对角线BD上一点,当线段AP的长度最短时,其长度记为t,则t的值是( )
A. B.1 C. D.2
4.如图,在正方形ABCD的外侧,作等边三角形CDE,连接AE.则∠DAE的度数是( )
A.15° B.20° C.12.5° D.10°
5.如图,在正方形ABCD中,E为AB中点,过点D作DF⊥DE交BC的延长线于点F,连接EF,若AE=1,则EF的值为( )
A.3 B. C.2 D.4
6.正方形具有矩形不一定有的性质是( )
A.对角互补 B.对角线相等
C.四个角相等 D.对角线互相垂直
7.下列性质中,矩形、正方形都具有,但是菱形却不具有的性质是( )
A.对角线长度相等 B.对角线互相垂直
C.对角线互相平分 D.一组对角线平分一组对角
8.如图,点D,E,F分别是△ABC三边的中点,则下列判断:
①四边形AEDF一定是平行四边形;②若AD平分∠A,则四边形AEDF是正方形;
③若AD⊥BC,则四边形AEDF是菱形;④若∠A=90°,则四边形AEDF是矩形.
正确的个数为( )
A.1 B.2 C.3 D.4
9.下列条件中,能使菱形ABCD为正方形的是( )
A.AB=AD B.AB⊥BC C.AC⊥BD D.AC平分∠BAD
10.如图E、F在矩形ABCD的对角线BD所在的直线上,BE=DF,则四边形AECF( )
A.平行四边形 B.矩形 C.菱形 D.正方形
11.如图,在正方形ABCD中,AB=4,E为对角线AC上与A,C不重合的一个动点,过点E作EF⊥AB于点F,EG⊥BC于点G,连接DE,FG,下列结论:①DE=FG;②DE⊥FG;③∠BFG=∠ADE;④FG的最小值为3.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
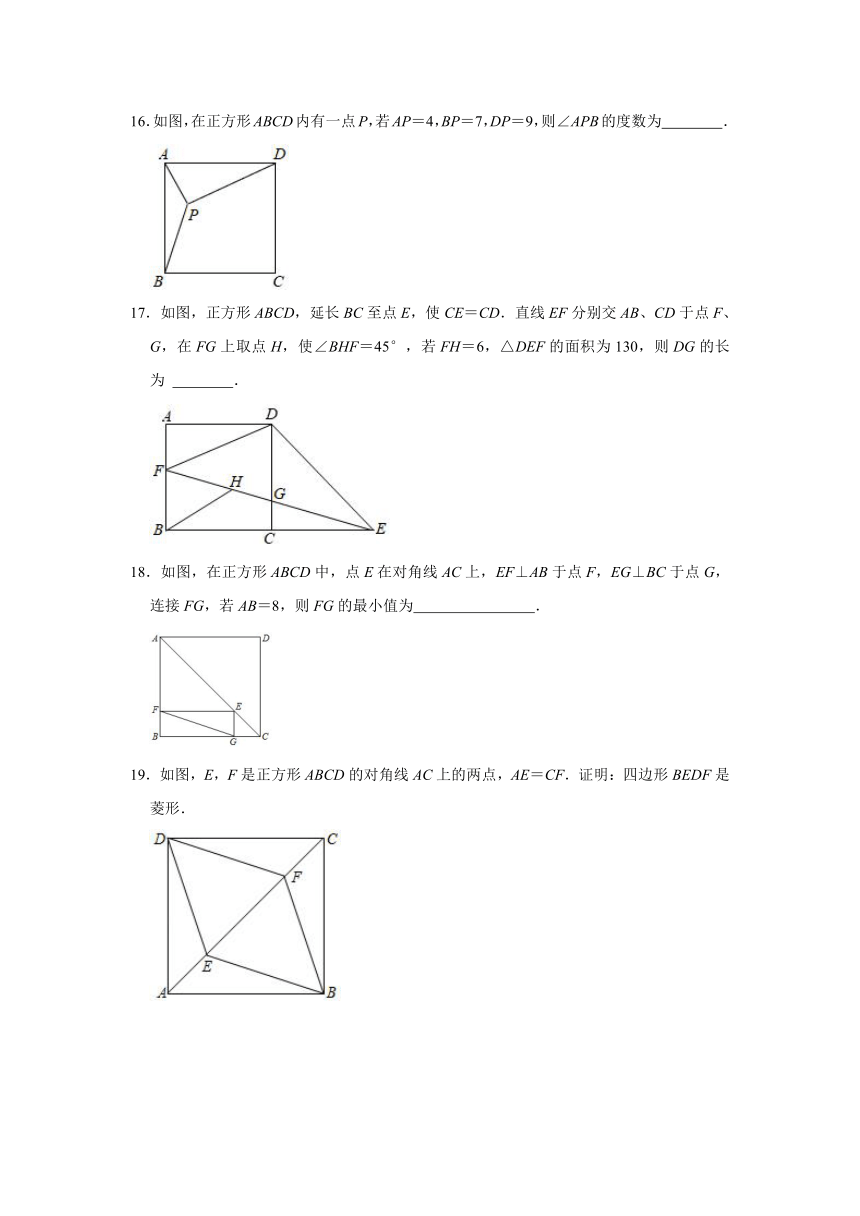
12.如图,菱形ABCD中,∠B=60°,AB=3,则以AC为边长的正方形ACEF的面积为( )
A.9 B.12 C.15 D.20
13.如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=2,若CE?DE=5,则正方形的面积为( )
A.5 B.6 C.7 D.8
14.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
15.如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )
A.60° B.67.5° C.75° D.54°
16.如图,在正方形ABCD内有一点P,若AP=4,BP=7,DP=9,则∠APB的度数为 .
17.如图,正方形ABCD,延长BC至点E,使CE=CD.直线EF分别交AB、CD于点F、G,在FG上取点H,使∠BHF=45°,若FH=6,△DEF的面积为130,则DG的长为 .
18.如图,在正方形ABCD中,点E在对角线AC上,EF⊥AB于点F,EG⊥BC于点G,连接FG,若AB=8,则FG的最小值为 .
19.如图,E,F是正方形ABCD的对角线AC上的两点,AE=CF.证明:四边形BEDF是菱形.
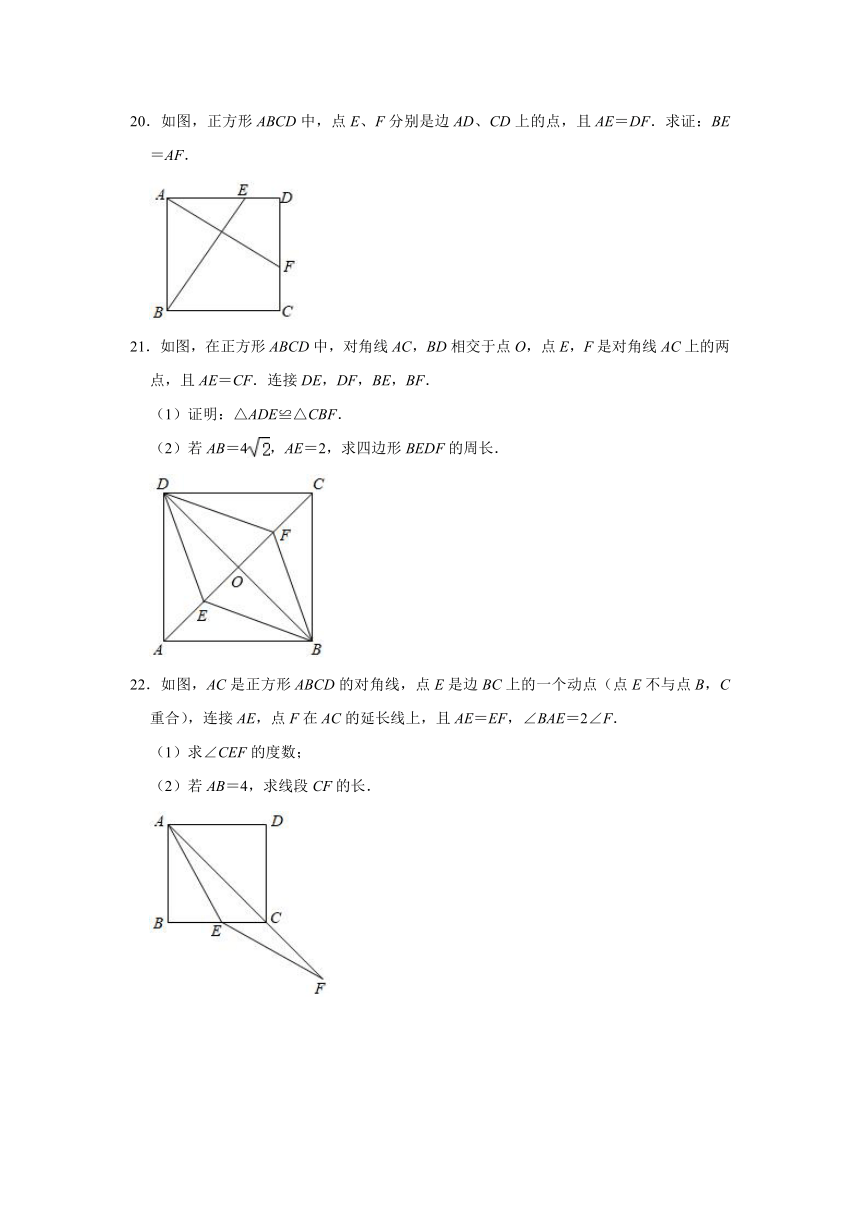
20.如图,正方形ABCD中,点E、F分别是边AD、CD上的点,且AE=DF.求证:BE=AF.
21.如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F是对角线AC上的两点,且AE=CF.连接DE,DF,BE,BF.
(1)证明:△ADE≌△CBF.
(2)若AB=4,AE=2,求四边形BEDF的周长.
22.如图,AC是正方形ABCD的对角线,点E是边BC上的一个动点(点E不与点B,C重合),连接AE,点F在AC的延长线上,且AE=EF,∠BAE=2∠F.
(1)求∠CEF的度数;
(2)若AB=4,求线段CF的长.
23.在正方形ABCD中,点E、F分别在BC边和CD上,且满足△AEF是等边三角形,连接AC交EF于点G.
(1)求证:CE=CF; (2)若等边△AEF边长为2,求AC的长.
24.如图,四边形ABCD为正方形,点E、F分别是AB、CD的中点,DG⊥CF于点G.
(1)求证:AE∥CF;
(2)求证:∠AGE=90°;
(3)若正方形的边长为2,求线段CG的长度.
25.如图,四边形ABCD是菱形,DE∥AC,CE∥BD.
(1)求证:四边形OCED是矩形.
(2)若∠ABC=60°,AB=2,求矩形OCED周长.
(3)当∠ABC= °时,四边形OCED是正方形.
26.如图,点P在正方形ABCD的对角线AC上,点E在边BC上,且PE=PB.
(1)求证:PE=PD;
(2)试探究BC2,EC2,PE2三者之间满足的等量关系,并证明你的结论.
27.如图,在正方形ABCD中,AB=,E为正方形ABCD内一点,DE=AB,∠EDC=α(0°<α<90°),连结CE,AE,过点D作DF⊥AE,垂足为点F,交CE的延长线于点G,连结AG.
(1)当α=20°时,求∠DAE的度数;
(2)判断△AEG的形状,并说明理由;
(3)当GF=1时,求CE的长.
28.如图,O是正方形ABCD对角线AC,BD的交点,AF平分∠BAC,交BD于点M,DE⊥AF于点H,分别交AB,AC于点E,G.
(1)证明△AED≌△BFA;
(2)△ADM是等腰三角形吗?请说明理由;
(3)若OG的长为1,求BE的长度.
29.已知边长为2的正方形ABCD中,P是对角线AC上的一个动点(与点A,C不重合),过点P作PE⊥PB,PE交DC于点E,过点E作EF⊥AC,垂足为点F.
(1)求证:PB=PE;
(2)在点P的运动过程中,PF的长度是否发生变化?若不变,求出这个不变的值;若变化,试说明理由.
参考答案
1.解:A、对角线相互平分的四边形是平行四边形,不符合题意;
B、对角线相等的平行四边形是矩形,符合题意;
C、对角线相互垂直平分的四边形是菱形,不符合题意;
D、对角线相互垂直且相等的平行四边形是正方形,不符合题意;
故选:B.
2.解:过点E作x轴的垂线EH,垂足为H.过点G作x轴的垂线GM,垂足为M,连接GE、FO交于点O′,
∵点E(2,3),
∴OH=2,EH=3,
∵四边形OEFG是正方形,
∴OG=EO,∠GOM=∠OEH,∠OGM=∠EOH,
在△OGM与△EOH中,
,
∴△OGM≌△EOH(ASA),
∴GM=OH=2,OM=EH=3,
∴G(﹣3,2).
∴O′(﹣,).
∵点F与点O关于点O′对称,
∴点F的坐标为 (﹣1,5).
故选:A.
3.解:∵四边形ABCD是正方形
∴AB=AD=1,∠BAD=90°,
∴BD==,
∵P为其对角线BD上一点,
∴当线段AP的长度最短时,AP⊥BD,此时PD=PB,
∴AP=BD=,即t=,
∴t=×=1.
故选:B.
4.解:∵四边形ABCD是正方形,
∴∠ADC=90°,AD=DC,
∵△CDE是等边三角形,
∴DE=DC,∠EDC=60°,
∴∠ADE=90°+60°=150°,AD=ED,
∴∠DAE=∠DEA=(180°﹣∠ADE)=15°,
故选:A.
5.解:∵四边形ABCD是正方形,
∴∠A=∠BCD=∠ADC=90°,AD=CD=AB=BC,
∴∠DCF=∠DCB=∠A=90°,
∵DF⊥DE,
∴∠EDF=90°,
∴∠CDF+∠EDC=90°,
∵∠ADE+∠EDC=90°,
∴∠CDF=∠ADE,
在△ADE与△CDF中,
,
∴△ADE≌△CDF(ASA),
∴CF=AE=1,
∵E为AB的中点,AE=1,
∴BE=AE=1,BC=AB=2AE=2,
∴BF=BC+CF=2+1=3,
在Rt△BEF中,根据勾股定理得:
EF===,
故选:B.
6.解:A、对角互补,正方形具有而矩形也具有,所以A选项不符合题意;
B、对角线相等,正方形具有而矩形也具有,所以B选项不符合题意;
C、四个角相等,正方形具有而矩形也具有,所以C选项不符合题意;
D、对角线互相垂直,正方形具有而矩形不具有,所以D选项符合题意.
故选:D.
7.解:∵菱形具有的性质是:两组对边分别平行,对角线互相平分,对角线互相垂直;
矩形具有的性质是:两组对边分别平行,对角线互相平分,对角线相等;
正方形具有菱形和矩形的性质,
∴菱形不具有的性质为:对角线长度相等,
故选:A.
8.解:①∵D是BC的中点,E是AB的中点,
∴DE∥AC.
∵D是BC的中点,F是AC的中点,
∴DF∥AB.
∴四边形AEDF是平行四边形.
∴①正确;
②如图,
由①知:AE∥DF,
∴∠EAD=∠ADF.
若AD平分∠BAC,
则∠EAD=∠FAD.
∴∠FAD=∠ADF,
∴AF=FD,
∵四边形AEDF是平行四边形,
∴四边形AEDF是菱形.
∴②不正确;
③如图,
若AD⊥BC,
∵D是BC的中点,
∴AD是BC的垂直平分线,
∴AB=AC.
∵AD⊥BC,E是AB的中点,
∴DE=AB.
同理:DF=AC,
∴DE=DF.
由①知:四边形AEDF是平行四边形,
∴四边形AEDF是菱形.
∴③正确;
④若∠A=90°,如图,
由①知:四边形AEDF是平行四边形,
∵∠A=90°,
∴四边形AEDF是矩形,
∴④正确;
综上可得,正确的结论有:①③④,
故选:C.
9.解:要使菱形成为正方形,只要菱形满足以下条件之一即可,(1)有一个内角是直角(2)对角线相等.
即∠ABC=90°或AC=BD.
故选:B.
10.解:A.∵四边形ABCD是矩形,
∴AO=CO,BO=DO,
∵BE=DF,
∴EO=FO,
∴四边形AECF是平行四边形,
故本选项符合题意;
B.∵四边形ABCD是矩形,
∴AC=BD,
∴AC≠EF,
∴四边形AECF不是矩形,
故本选项不符合题意;
C.∵四边形ABCD是矩形,
∴不能证明AC⊥BD,
∴不能证明AC⊥EF,
故本选项不符合题意;
D.∵四边形ABCD是矩形,
∴AC=BD,
∴AC≠EF,
∴四边形AECF不是正方形,
故本选项不符合题意;故选:A.
11.解:①连接BE,交FG于点O,如图,
∵EF⊥AB,EG⊥BC,
∴∠EFB=∠EGB=90°.
∵∠ABC=90°,
∴四边形EFBG为矩形.
∴FG=BE,OB=OF=OE=OG.
∵四边形ABCD为正方形,
∴AB=AD,∠BAC=∠DAC=45°.
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS).
∴BE=DE.
∴DE=FG.
∴①正确;
②∵△ABE≌△ADE,
∴∠ABE=∠ADE.
由①知:OB=OF,
∴∠OFB=∠ABE.
∴∠OFB=∠ADE.
∵∠BAD=90°,
∴∠ADE+∠AHD=90°.
∴∠OFB+∠AHD=90°.
即:∠FMH=90°,
∴DE⊥FG.
∴②正确;
③由②知:∠OFB=∠ADE.
即:∠BFG=∠ADE.
∴③正确;
④∵点E为AC上一动点,
∴根据垂线段最短,当DE⊥AC时,DE最小.
∵AD=CD=4,∠ADC=90°,
∴AC=.
∴DE=AC=2.
由①知:FG=DE,
∴FG的最小值为2,
∴④错误.
综上,正确的结论为:①②③.故选:C.
12.解:∵菱形ABCD,
∴AB=BC=3,
∵∠B=60°,
∴△ABC是等边三角形,
∴AC=AB=3,
∴正方形ACEF的边长为3,
∴正方形ACEF的面积为9,故选:A.
13.解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,
∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵∠COM+∠DOM=∠DON+∠DOM,
∴∠COM=∠DON,
∵四边形ABCD是正方形,
∴OC=OD,
在△COM和△DON中,
,
∴△COM≌△DON(AAS),
∴OM=ON,CM=DN,
∴四边形OMEN是正方形,
在Rt△OEN中,
∵OE=2,
∴2NE2=OE2=(2)2=8,
∴NE=ON=2,
∵DE+CE=DE+EM+MC=DE+EM+DN=EN+EM=2EN=4,
设DE=a,CE=b,
∴a+b=4,
∵CE?DE=5,
∴CD2=a2+b2=(a+b)2﹣2ab=42﹣2×5=6,
∴S正方形ABCD=6,
故选:B.
14.解:∵四边形ABCD是正方形,
∴∠MDO=∠NCO=45°,OD=OC,∠DOC=90°,
∴∠DON+∠CON=90°,
∵ON⊥OM,
∴∠MON=90°,
∴∠DON+∠DOM=90°,
∴∠DOM=∠CON,
在△DOM和△CON中,
,
∴△DOM≌△CON(ASA),
∵四边形MOND的面积是1,四边形MOND的面积=△DOM的面积+△DON的面积,
∴四边形MOND的面积=△CON的面积+△DON的面积=△DOC的面积,
∴△DOC的面积是1,
∴正方形ABCD的面积是4,
∵AB2=4,
∴AB=2,
故选:C.
15.解:连接BF.易知∠FCB=15°,∠DOC=∠OBC+∠FCB=45°+15°=60°
故选A.
16.解:∵四边形ABCD为正方形,
∴∠ABC=90°,BA=BC,
∴△BAP绕点A逆时针旋转90°可得△ADE,
连接PE,
由旋转的性质得,ED=BP=7,AE=AP=4,∠PBE=90°,∠AED=∠APB,
∴△APE为等腰直角三角形,
∴PE=AP=4,∠AEP=45°,
在△PED中,∵PD=9,ED=7,PE=4,
∴DE2+PE2=DP2,
∴△PED为直角三角形,∠PED=90°,
∴∠AED=90°+45°=135°,
∴∠APB=135°,
故答案为:135°.
17.解:连接DH,
∵四边形ABCD是正方形,
∴∠A=∠ABC=90°,
∴∠BFE=90°﹣∠BEF,
∵∠DFE=180°﹣∠FDE﹣∠DEF,∠AFD=180°﹣∠DFE﹣∠BFE,∠BFE=180°﹣∠FHB﹣∠FBH且∠BHF=45°,
∴∠DFH=45°=∠FHB,
∴DF∥BH,
∴∠BAF+∠FHD+∠FDH=180°,
∴∠BHF=∠FBH=45°,
∴∠DHF=90°,
∴△FHD为等腰直角三角形,
∴DH=6,
∵S△FDG=S△DGE==65(底与高相等,面积也相等),
∴FG?DH÷2=DG?AD÷2=65,
∴DG=6.5.
故答案为:6.5.
18.解:连接BE,如图:
∵四边形ABCD是正方形,
∴∠ABC=90°,
又EF⊥AB于点F,EG⊥BC,
∴四边形FBGE是矩形,
∴FG=BE,
所以当BE最小时,FG就最小,
根据垂线段最短,可知当BE⊥AC时,BE最小,
当BE⊥AC时,在正方形ABCD中,△AEB是等腰直角三角形,
在Rt△ABE中,根据勾股定理可得2BE2=AB2=64,解得BE=4,
∴FG最小为4;
故答案为4.
19.证明:连接BD交AC于点O,如图,
∵四边形ABCD为正方形,
∴BD⊥AC,OD=OB=OA=OC
∵AE=CF,
∴OA﹣AE=OC﹣CF,
即OE=OF,
∵OD=OB,
∴四边形BEDF为平行四边形,
∵BD⊥EF,
∴平行四边形BEDF为菱形.
20.证明:∵四边形ABCD是正方形,
∴∠BAE=∠ADF=90°,AB=AD,
又∵AE=DF,
在Rt△BAE和Rt△ADF中,
,
∴Rt△BAE≌Rt△ADF(HL),
∴BE=AF.
21.(1)证明:由正方形对角线平分每一组对角可知:∠DAE=∠BCF=45°,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS).
(2)解:∵AB=AD=,
∴BD===8,
由正方形对角线相等且互相垂直平分可得:AC=BD=8,DO=BO=4,OA=OC=4,
又AE=CF=2,
∴OA﹣AE=OC﹣CF,
即OE=OF=4﹣2=2,
故四边形BEDF为菱形.
∵∠DOE=90°,
∴DE===2.
∴4DE=
故四边形BEDF的周长为8.
22.解:(1)∵AC是正方形ABCD的对角线,
∴∠BAC=∠ACB=45°,
∵AE=EF,
∴∠F=∠EAF,
∵∠BAE=2∠F,
∴∠BAE=2∠F=2∠EAF,
∵∠BAC=∠BAE+∠EAF=45°,
∴∠CEF=30°.
(2)过E点作EG⊥AC于G,
∵ABCD为正方形,AC为对角线,
∴∠ACB=45°,
∴△EGC为等腰直角三角形,EG=GC,
由(1)可知∠BAE=30°,AB=4,
∴BE=AE,
∵;AB2+BE2=AE2AB2+BE2=AE2,即42+BE2=4BE2,
∴BE=,
∴EC=4﹣
∵EG2+GC2=FC2EG2+GC2=EC2,EG=GC,
∴GC=,
∵正方形ABCD中,AB=4,AC为对角线,
∴AC=,
∵AE=EF,EG⊥AF,
∴AG=GF,
∴CF=GF﹣CG=AG﹣CG=AC﹣2GC=.
23.证明:(1)∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,BC=CD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,
∴Rt△ABE≌Rt△ADF( HL),
∴BE=DF,
∴CE=CF.
(2)∵AE=AF,CE=CF,
∴AC垂直平分EF,
∴EG=FG=1.
∴,,
∴.
24.解:(1)∵AF=CE,AF=CE,
∴四边形AFCE是平行四边形,
∴AE∥CF;
(2)如图,取AE和DG交于H,
∵CF∥AE,DG⊥CF,
∴DG⊥AE于H,
∵E是CD的中点,
∴EG=ED,
∴△DGE是等腰三角形,
∴H是DG的中点,
∴AG=AD,
在△ADE和△AGE中,
,
∴△ADE≌△AGE(SSS),
∴∠AGE=∠ADE=90°;
(3)∵AG=AD=2,DE=1,
∴AE=,
又∵GH⊥AE,
∴,
解得HG=,
∴DG=,
∴,
故答案为.
25.(1)证明:∵DE∥AC,CE∥BD,
即DE∥OC,CE∥OD,
∴四边形OCED是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∴四边形OCED是矩形;
(2)∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOB=90°,∠ABO=ABC,
∵∠ABC=60°,
∴∠ABO=30°,
∵AB=2,
∴AO=AB=1,OB=AB=,
∵OD=OB=,OC=OA=1,
∴矩形OCED周长=2(OD+OC)=2+2;
(3)当∠ABC=90°时,四边形OCED是正方形,
∵∠ABC=90°,四边形ABCD是菱形,
∴四边形ABCD是正方形,
∴AC=BD,
∴OD=OC,
∵四边形OCED是矩形,
∴四边形OCED是正方形,
故答案为:90.
26.(1)证明:∵四边形ABCD是正方形,
∴BC=DC,∠ACB=∠ACD,
在△PBC和△PDC中,
,
∴△PBC≌△PDC(SAS),
∴PB=PD,
∵PE=PB,
∴PE=PD;
(2)解:BC2+EC2=2PE2,证明如下:
连接DE,如图所示:
∵四边形ABCD是正方形,
∴∠BCD=90°,BC=CD,
由(1)得:△PBC≌△PDC,
∴∠PBC=∠PDC,
∵PE=PB,
∴∠PBC=∠PEB,
∴∠PDC=∠PEB,
∵∠PEB+∠PEC=180°,
∴∠PDC+∠PEC=180°,
∴∠EPD=360°﹣(∠PDC+∠PEC)﹣∠BCD=360°﹣180°﹣90°=90°,
又∵PE=PD,
∴△PDE是等腰直角三角形,
∴DE2=PE2+PD2=2PE2,
在Rt△CDE中,由勾股定理得:CD2+EC2=DE2,
∴BC2+EC2=2PE2.
27.解:(1)∵四边形ABCD是正方形,
∴∠ADC=90°,AB=AD,
∵∠CDE=20°,
∴∠ADE=70°,
∵DE=AB,
∴DA=DE,
∴∠DAE=∠DEA=×(180°﹣70°)=55°.
(2)结论:△AEG是等腰直角三角形.
理由:∵AD=DE,DF⊥AE,
∴DG是AE的垂直平分线,
∴AG=GE,
∴∠GAE=∠GEA,
∵DE=DC=AD,
∴∠DAE=∠DEA,∠DEC=∠DCE,
∵∠DAE+∠DEA+∠DEC+∠DCE+∠ADC=360°,
∴∠DEA+∠DEC=135°,
∴∠GEA=45°,
∴∠GAE=∠GEA=45°,
∴∠AGE=90°,
∴△AEG为等腰直角三角形.
(3)如图,连接AC,
∵四边形ABCD是正方形,
∴AC=AB=,
∵△AEG为等腰直角三角形,GF⊥AE,
∴GF=AF=EF=1,
∴AG=GE=,
∵AC2=AG2+GC2,
∴10=2+(EC+)2,
∴EC=(负根已经舍弃).
28.解:(1)∵四边形ABCD为正方形,
∴∠DAE=∠ABF=90°,AD=AB,
∵DE⊥AF,
∴∠DAH+∠ADE=90°,
∵∠DAH+∠BAF=90°,
∴∠ADE=∠BAF,
在△AED和△BFA中,
,
∴△AED≌△BFA(ASA).
(2)△ADM是等腰三角形,理由如下:
∵∠BAC=45°,AF平分∠BAC,
∴∠BAF=∠CAF=∠BAC=22.5°,
∴∠DAM=∠DAC+∠CAF=67.5°,
∴∠DMA=180°﹣∠DAM﹣∠ADM=180°﹣67.5°﹣45°=67.5°,
∴∠DAM=∠DMA,
∴△ADM是等腰三角形.
(3)∵∠ADE=∠BAF=22.5°,
∴∠CDG=∠ADC﹣∠ADE=67.5°,
∴∠DGC=180°﹣∠GCD﹣∠CDG=67.5°,
∴CG=CB,
∵AE∥CD,
∴∠AEG=∠CDG=67.5°,
∴AE=AG,
如图,作FK⊥AC于点K,设AG=AE=x,
∵AO=AG+OG=x+1,
∴AB=BC=AO=(x+1),AC=2AO=2(x+1),
∵△AED≌△BFA,
∴BF=AE=x,
∵AF平分∠BAC,
∴FK=BF=x,
∵S△ABF=AB?BF,S△ACF=AC?FK,
∴==,
又∵=,
∴==,
即=,
解得x=,
∴BE=AB﹣AE=(x+1)﹣x=2.
29.(1)证明:过点P作PG⊥BC于G,过点P作PH⊥DC于H,如图1.
∵四边形ABCD是正方形,PG⊥BC,PH⊥DC,
∴∠GPC=∠ACB=∠ACD=∠HPC=45°.
∴PG=PH,∠GPH=∠PGB=∠PHE=90°.
∵PE⊥PB,即∠BPE=90°,
∴∠BPG=90°﹣∠GPE=∠EPH.
在△PGB和△PHE中,
,
∴△PGB≌△PHE(ASA),
∴PB=PE.
(2)解:PF的长度不变.
连接BD,如图2.
∵四边形ABCD是正方形,
∴∠BOP=90°,
∵PE⊥PB,即∠BPE=90°,
∴∠PBO=90°﹣∠BPO=∠EPF,
∵EF⊥PC,即∠PFE=90°,
∴∠BOP=∠PFE,
在△BOP和△PFE中,
,
∴△BOP≌△PFE(AAS),
∴BO=PF.
∵四边形ABCD是正方形,
∴OB=OC,∠BOC=90°,
∴BC=OB.
∵BC=2,
∴OB=,
∴PF=OB=.
∴点P在运动过程中,PF的长度不变,值为.
1.下列说法判断错误的是( )
A.对角线相互平分的四边形是平行四边形 B.对角线相等的四边形是矩形
C.对角线相互垂直平分的四边形是菱形D.对角线相互垂直且相等的平行四边形是正方形
2.如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E(2,3),则点F的坐标为( )
A.(﹣1,5) B.(﹣2,3) C.(5,﹣1) D.(﹣3,2)
3.如图,在正方形ABCD中,AB=1,P为其对角线BD上一点,当线段AP的长度最短时,其长度记为t,则t的值是( )
A. B.1 C. D.2
4.如图,在正方形ABCD的外侧,作等边三角形CDE,连接AE.则∠DAE的度数是( )
A.15° B.20° C.12.5° D.10°
5.如图,在正方形ABCD中,E为AB中点,过点D作DF⊥DE交BC的延长线于点F,连接EF,若AE=1,则EF的值为( )
A.3 B. C.2 D.4
6.正方形具有矩形不一定有的性质是( )
A.对角互补 B.对角线相等
C.四个角相等 D.对角线互相垂直
7.下列性质中,矩形、正方形都具有,但是菱形却不具有的性质是( )
A.对角线长度相等 B.对角线互相垂直
C.对角线互相平分 D.一组对角线平分一组对角
8.如图,点D,E,F分别是△ABC三边的中点,则下列判断:
①四边形AEDF一定是平行四边形;②若AD平分∠A,则四边形AEDF是正方形;
③若AD⊥BC,则四边形AEDF是菱形;④若∠A=90°,则四边形AEDF是矩形.
正确的个数为( )
A.1 B.2 C.3 D.4
9.下列条件中,能使菱形ABCD为正方形的是( )
A.AB=AD B.AB⊥BC C.AC⊥BD D.AC平分∠BAD
10.如图E、F在矩形ABCD的对角线BD所在的直线上,BE=DF,则四边形AECF( )
A.平行四边形 B.矩形 C.菱形 D.正方形
11.如图,在正方形ABCD中,AB=4,E为对角线AC上与A,C不重合的一个动点,过点E作EF⊥AB于点F,EG⊥BC于点G,连接DE,FG,下列结论:①DE=FG;②DE⊥FG;③∠BFG=∠ADE;④FG的最小值为3.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
12.如图,菱形ABCD中,∠B=60°,AB=3,则以AC为边长的正方形ACEF的面积为( )
A.9 B.12 C.15 D.20
13.如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=2,若CE?DE=5,则正方形的面积为( )
A.5 B.6 C.7 D.8
14.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
15.如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )
A.60° B.67.5° C.75° D.54°
16.如图,在正方形ABCD内有一点P,若AP=4,BP=7,DP=9,则∠APB的度数为 .
17.如图,正方形ABCD,延长BC至点E,使CE=CD.直线EF分别交AB、CD于点F、G,在FG上取点H,使∠BHF=45°,若FH=6,△DEF的面积为130,则DG的长为 .
18.如图,在正方形ABCD中,点E在对角线AC上,EF⊥AB于点F,EG⊥BC于点G,连接FG,若AB=8,则FG的最小值为 .
19.如图,E,F是正方形ABCD的对角线AC上的两点,AE=CF.证明:四边形BEDF是菱形.
20.如图,正方形ABCD中,点E、F分别是边AD、CD上的点,且AE=DF.求证:BE=AF.
21.如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F是对角线AC上的两点,且AE=CF.连接DE,DF,BE,BF.
(1)证明:△ADE≌△CBF.
(2)若AB=4,AE=2,求四边形BEDF的周长.
22.如图,AC是正方形ABCD的对角线,点E是边BC上的一个动点(点E不与点B,C重合),连接AE,点F在AC的延长线上,且AE=EF,∠BAE=2∠F.
(1)求∠CEF的度数;
(2)若AB=4,求线段CF的长.
23.在正方形ABCD中,点E、F分别在BC边和CD上,且满足△AEF是等边三角形,连接AC交EF于点G.
(1)求证:CE=CF; (2)若等边△AEF边长为2,求AC的长.
24.如图,四边形ABCD为正方形,点E、F分别是AB、CD的中点,DG⊥CF于点G.
(1)求证:AE∥CF;
(2)求证:∠AGE=90°;
(3)若正方形的边长为2,求线段CG的长度.
25.如图,四边形ABCD是菱形,DE∥AC,CE∥BD.
(1)求证:四边形OCED是矩形.
(2)若∠ABC=60°,AB=2,求矩形OCED周长.
(3)当∠ABC= °时,四边形OCED是正方形.
26.如图,点P在正方形ABCD的对角线AC上,点E在边BC上,且PE=PB.
(1)求证:PE=PD;
(2)试探究BC2,EC2,PE2三者之间满足的等量关系,并证明你的结论.
27.如图,在正方形ABCD中,AB=,E为正方形ABCD内一点,DE=AB,∠EDC=α(0°<α<90°),连结CE,AE,过点D作DF⊥AE,垂足为点F,交CE的延长线于点G,连结AG.
(1)当α=20°时,求∠DAE的度数;
(2)判断△AEG的形状,并说明理由;
(3)当GF=1时,求CE的长.
28.如图,O是正方形ABCD对角线AC,BD的交点,AF平分∠BAC,交BD于点M,DE⊥AF于点H,分别交AB,AC于点E,G.
(1)证明△AED≌△BFA;
(2)△ADM是等腰三角形吗?请说明理由;
(3)若OG的长为1,求BE的长度.
29.已知边长为2的正方形ABCD中,P是对角线AC上的一个动点(与点A,C不重合),过点P作PE⊥PB,PE交DC于点E,过点E作EF⊥AC,垂足为点F.
(1)求证:PB=PE;
(2)在点P的运动过程中,PF的长度是否发生变化?若不变,求出这个不变的值;若变化,试说明理由.
参考答案
1.解:A、对角线相互平分的四边形是平行四边形,不符合题意;
B、对角线相等的平行四边形是矩形,符合题意;
C、对角线相互垂直平分的四边形是菱形,不符合题意;
D、对角线相互垂直且相等的平行四边形是正方形,不符合题意;
故选:B.
2.解:过点E作x轴的垂线EH,垂足为H.过点G作x轴的垂线GM,垂足为M,连接GE、FO交于点O′,
∵点E(2,3),
∴OH=2,EH=3,
∵四边形OEFG是正方形,
∴OG=EO,∠GOM=∠OEH,∠OGM=∠EOH,
在△OGM与△EOH中,
,
∴△OGM≌△EOH(ASA),
∴GM=OH=2,OM=EH=3,
∴G(﹣3,2).
∴O′(﹣,).
∵点F与点O关于点O′对称,
∴点F的坐标为 (﹣1,5).
故选:A.
3.解:∵四边形ABCD是正方形
∴AB=AD=1,∠BAD=90°,
∴BD==,
∵P为其对角线BD上一点,
∴当线段AP的长度最短时,AP⊥BD,此时PD=PB,
∴AP=BD=,即t=,
∴t=×=1.
故选:B.
4.解:∵四边形ABCD是正方形,
∴∠ADC=90°,AD=DC,
∵△CDE是等边三角形,
∴DE=DC,∠EDC=60°,
∴∠ADE=90°+60°=150°,AD=ED,
∴∠DAE=∠DEA=(180°﹣∠ADE)=15°,
故选:A.
5.解:∵四边形ABCD是正方形,
∴∠A=∠BCD=∠ADC=90°,AD=CD=AB=BC,
∴∠DCF=∠DCB=∠A=90°,
∵DF⊥DE,
∴∠EDF=90°,
∴∠CDF+∠EDC=90°,
∵∠ADE+∠EDC=90°,
∴∠CDF=∠ADE,
在△ADE与△CDF中,
,
∴△ADE≌△CDF(ASA),
∴CF=AE=1,
∵E为AB的中点,AE=1,
∴BE=AE=1,BC=AB=2AE=2,
∴BF=BC+CF=2+1=3,
在Rt△BEF中,根据勾股定理得:
EF===,
故选:B.
6.解:A、对角互补,正方形具有而矩形也具有,所以A选项不符合题意;
B、对角线相等,正方形具有而矩形也具有,所以B选项不符合题意;
C、四个角相等,正方形具有而矩形也具有,所以C选项不符合题意;
D、对角线互相垂直,正方形具有而矩形不具有,所以D选项符合题意.
故选:D.
7.解:∵菱形具有的性质是:两组对边分别平行,对角线互相平分,对角线互相垂直;
矩形具有的性质是:两组对边分别平行,对角线互相平分,对角线相等;
正方形具有菱形和矩形的性质,
∴菱形不具有的性质为:对角线长度相等,
故选:A.
8.解:①∵D是BC的中点,E是AB的中点,
∴DE∥AC.
∵D是BC的中点,F是AC的中点,
∴DF∥AB.
∴四边形AEDF是平行四边形.
∴①正确;
②如图,
由①知:AE∥DF,
∴∠EAD=∠ADF.
若AD平分∠BAC,
则∠EAD=∠FAD.
∴∠FAD=∠ADF,
∴AF=FD,
∵四边形AEDF是平行四边形,
∴四边形AEDF是菱形.
∴②不正确;
③如图,
若AD⊥BC,
∵D是BC的中点,
∴AD是BC的垂直平分线,
∴AB=AC.
∵AD⊥BC,E是AB的中点,
∴DE=AB.
同理:DF=AC,
∴DE=DF.
由①知:四边形AEDF是平行四边形,
∴四边形AEDF是菱形.
∴③正确;
④若∠A=90°,如图,
由①知:四边形AEDF是平行四边形,
∵∠A=90°,
∴四边形AEDF是矩形,
∴④正确;
综上可得,正确的结论有:①③④,
故选:C.
9.解:要使菱形成为正方形,只要菱形满足以下条件之一即可,(1)有一个内角是直角(2)对角线相等.
即∠ABC=90°或AC=BD.
故选:B.
10.解:A.∵四边形ABCD是矩形,
∴AO=CO,BO=DO,
∵BE=DF,
∴EO=FO,
∴四边形AECF是平行四边形,
故本选项符合题意;
B.∵四边形ABCD是矩形,
∴AC=BD,
∴AC≠EF,
∴四边形AECF不是矩形,
故本选项不符合题意;
C.∵四边形ABCD是矩形,
∴不能证明AC⊥BD,
∴不能证明AC⊥EF,
故本选项不符合题意;
D.∵四边形ABCD是矩形,
∴AC=BD,
∴AC≠EF,
∴四边形AECF不是正方形,
故本选项不符合题意;故选:A.
11.解:①连接BE,交FG于点O,如图,
∵EF⊥AB,EG⊥BC,
∴∠EFB=∠EGB=90°.
∵∠ABC=90°,
∴四边形EFBG为矩形.
∴FG=BE,OB=OF=OE=OG.
∵四边形ABCD为正方形,
∴AB=AD,∠BAC=∠DAC=45°.
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS).
∴BE=DE.
∴DE=FG.
∴①正确;
②∵△ABE≌△ADE,
∴∠ABE=∠ADE.
由①知:OB=OF,
∴∠OFB=∠ABE.
∴∠OFB=∠ADE.
∵∠BAD=90°,
∴∠ADE+∠AHD=90°.
∴∠OFB+∠AHD=90°.
即:∠FMH=90°,
∴DE⊥FG.
∴②正确;
③由②知:∠OFB=∠ADE.
即:∠BFG=∠ADE.
∴③正确;
④∵点E为AC上一动点,
∴根据垂线段最短,当DE⊥AC时,DE最小.
∵AD=CD=4,∠ADC=90°,
∴AC=.
∴DE=AC=2.
由①知:FG=DE,
∴FG的最小值为2,
∴④错误.
综上,正确的结论为:①②③.故选:C.
12.解:∵菱形ABCD,
∴AB=BC=3,
∵∠B=60°,
∴△ABC是等边三角形,
∴AC=AB=3,
∴正方形ACEF的边长为3,
∴正方形ACEF的面积为9,故选:A.
13.解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,
∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵∠COM+∠DOM=∠DON+∠DOM,
∴∠COM=∠DON,
∵四边形ABCD是正方形,
∴OC=OD,
在△COM和△DON中,
,
∴△COM≌△DON(AAS),
∴OM=ON,CM=DN,
∴四边形OMEN是正方形,
在Rt△OEN中,
∵OE=2,
∴2NE2=OE2=(2)2=8,
∴NE=ON=2,
∵DE+CE=DE+EM+MC=DE+EM+DN=EN+EM=2EN=4,
设DE=a,CE=b,
∴a+b=4,
∵CE?DE=5,
∴CD2=a2+b2=(a+b)2﹣2ab=42﹣2×5=6,
∴S正方形ABCD=6,
故选:B.
14.解:∵四边形ABCD是正方形,
∴∠MDO=∠NCO=45°,OD=OC,∠DOC=90°,
∴∠DON+∠CON=90°,
∵ON⊥OM,
∴∠MON=90°,
∴∠DON+∠DOM=90°,
∴∠DOM=∠CON,
在△DOM和△CON中,
,
∴△DOM≌△CON(ASA),
∵四边形MOND的面积是1,四边形MOND的面积=△DOM的面积+△DON的面积,
∴四边形MOND的面积=△CON的面积+△DON的面积=△DOC的面积,
∴△DOC的面积是1,
∴正方形ABCD的面积是4,
∵AB2=4,
∴AB=2,
故选:C.
15.解:连接BF.易知∠FCB=15°,∠DOC=∠OBC+∠FCB=45°+15°=60°
故选A.
16.解:∵四边形ABCD为正方形,
∴∠ABC=90°,BA=BC,
∴△BAP绕点A逆时针旋转90°可得△ADE,
连接PE,
由旋转的性质得,ED=BP=7,AE=AP=4,∠PBE=90°,∠AED=∠APB,
∴△APE为等腰直角三角形,
∴PE=AP=4,∠AEP=45°,
在△PED中,∵PD=9,ED=7,PE=4,
∴DE2+PE2=DP2,
∴△PED为直角三角形,∠PED=90°,
∴∠AED=90°+45°=135°,
∴∠APB=135°,
故答案为:135°.
17.解:连接DH,
∵四边形ABCD是正方形,
∴∠A=∠ABC=90°,
∴∠BFE=90°﹣∠BEF,
∵∠DFE=180°﹣∠FDE﹣∠DEF,∠AFD=180°﹣∠DFE﹣∠BFE,∠BFE=180°﹣∠FHB﹣∠FBH且∠BHF=45°,
∴∠DFH=45°=∠FHB,
∴DF∥BH,
∴∠BAF+∠FHD+∠FDH=180°,
∴∠BHF=∠FBH=45°,
∴∠DHF=90°,
∴△FHD为等腰直角三角形,
∴DH=6,
∵S△FDG=S△DGE==65(底与高相等,面积也相等),
∴FG?DH÷2=DG?AD÷2=65,
∴DG=6.5.
故答案为:6.5.
18.解:连接BE,如图:
∵四边形ABCD是正方形,
∴∠ABC=90°,
又EF⊥AB于点F,EG⊥BC,
∴四边形FBGE是矩形,
∴FG=BE,
所以当BE最小时,FG就最小,
根据垂线段最短,可知当BE⊥AC时,BE最小,
当BE⊥AC时,在正方形ABCD中,△AEB是等腰直角三角形,
在Rt△ABE中,根据勾股定理可得2BE2=AB2=64,解得BE=4,
∴FG最小为4;
故答案为4.
19.证明:连接BD交AC于点O,如图,
∵四边形ABCD为正方形,
∴BD⊥AC,OD=OB=OA=OC
∵AE=CF,
∴OA﹣AE=OC﹣CF,
即OE=OF,
∵OD=OB,
∴四边形BEDF为平行四边形,
∵BD⊥EF,
∴平行四边形BEDF为菱形.
20.证明:∵四边形ABCD是正方形,
∴∠BAE=∠ADF=90°,AB=AD,
又∵AE=DF,
在Rt△BAE和Rt△ADF中,
,
∴Rt△BAE≌Rt△ADF(HL),
∴BE=AF.
21.(1)证明:由正方形对角线平分每一组对角可知:∠DAE=∠BCF=45°,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS).
(2)解:∵AB=AD=,
∴BD===8,
由正方形对角线相等且互相垂直平分可得:AC=BD=8,DO=BO=4,OA=OC=4,
又AE=CF=2,
∴OA﹣AE=OC﹣CF,
即OE=OF=4﹣2=2,
故四边形BEDF为菱形.
∵∠DOE=90°,
∴DE===2.
∴4DE=
故四边形BEDF的周长为8.
22.解:(1)∵AC是正方形ABCD的对角线,
∴∠BAC=∠ACB=45°,
∵AE=EF,
∴∠F=∠EAF,
∵∠BAE=2∠F,
∴∠BAE=2∠F=2∠EAF,
∵∠BAC=∠BAE+∠EAF=45°,
∴∠CEF=30°.
(2)过E点作EG⊥AC于G,
∵ABCD为正方形,AC为对角线,
∴∠ACB=45°,
∴△EGC为等腰直角三角形,EG=GC,
由(1)可知∠BAE=30°,AB=4,
∴BE=AE,
∵;AB2+BE2=AE2AB2+BE2=AE2,即42+BE2=4BE2,
∴BE=,
∴EC=4﹣
∵EG2+GC2=FC2EG2+GC2=EC2,EG=GC,
∴GC=,
∵正方形ABCD中,AB=4,AC为对角线,
∴AC=,
∵AE=EF,EG⊥AF,
∴AG=GF,
∴CF=GF﹣CG=AG﹣CG=AC﹣2GC=.
23.证明:(1)∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,BC=CD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,
∴Rt△ABE≌Rt△ADF( HL),
∴BE=DF,
∴CE=CF.
(2)∵AE=AF,CE=CF,
∴AC垂直平分EF,
∴EG=FG=1.
∴,,
∴.
24.解:(1)∵AF=CE,AF=CE,
∴四边形AFCE是平行四边形,
∴AE∥CF;
(2)如图,取AE和DG交于H,
∵CF∥AE,DG⊥CF,
∴DG⊥AE于H,
∵E是CD的中点,
∴EG=ED,
∴△DGE是等腰三角形,
∴H是DG的中点,
∴AG=AD,
在△ADE和△AGE中,
,
∴△ADE≌△AGE(SSS),
∴∠AGE=∠ADE=90°;
(3)∵AG=AD=2,DE=1,
∴AE=,
又∵GH⊥AE,
∴,
解得HG=,
∴DG=,
∴,
故答案为.
25.(1)证明:∵DE∥AC,CE∥BD,
即DE∥OC,CE∥OD,
∴四边形OCED是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∴四边形OCED是矩形;
(2)∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOB=90°,∠ABO=ABC,
∵∠ABC=60°,
∴∠ABO=30°,
∵AB=2,
∴AO=AB=1,OB=AB=,
∵OD=OB=,OC=OA=1,
∴矩形OCED周长=2(OD+OC)=2+2;
(3)当∠ABC=90°时,四边形OCED是正方形,
∵∠ABC=90°,四边形ABCD是菱形,
∴四边形ABCD是正方形,
∴AC=BD,
∴OD=OC,
∵四边形OCED是矩形,
∴四边形OCED是正方形,
故答案为:90.
26.(1)证明:∵四边形ABCD是正方形,
∴BC=DC,∠ACB=∠ACD,
在△PBC和△PDC中,
,
∴△PBC≌△PDC(SAS),
∴PB=PD,
∵PE=PB,
∴PE=PD;
(2)解:BC2+EC2=2PE2,证明如下:
连接DE,如图所示:
∵四边形ABCD是正方形,
∴∠BCD=90°,BC=CD,
由(1)得:△PBC≌△PDC,
∴∠PBC=∠PDC,
∵PE=PB,
∴∠PBC=∠PEB,
∴∠PDC=∠PEB,
∵∠PEB+∠PEC=180°,
∴∠PDC+∠PEC=180°,
∴∠EPD=360°﹣(∠PDC+∠PEC)﹣∠BCD=360°﹣180°﹣90°=90°,
又∵PE=PD,
∴△PDE是等腰直角三角形,
∴DE2=PE2+PD2=2PE2,
在Rt△CDE中,由勾股定理得:CD2+EC2=DE2,
∴BC2+EC2=2PE2.
27.解:(1)∵四边形ABCD是正方形,
∴∠ADC=90°,AB=AD,
∵∠CDE=20°,
∴∠ADE=70°,
∵DE=AB,
∴DA=DE,
∴∠DAE=∠DEA=×(180°﹣70°)=55°.
(2)结论:△AEG是等腰直角三角形.
理由:∵AD=DE,DF⊥AE,
∴DG是AE的垂直平分线,
∴AG=GE,
∴∠GAE=∠GEA,
∵DE=DC=AD,
∴∠DAE=∠DEA,∠DEC=∠DCE,
∵∠DAE+∠DEA+∠DEC+∠DCE+∠ADC=360°,
∴∠DEA+∠DEC=135°,
∴∠GEA=45°,
∴∠GAE=∠GEA=45°,
∴∠AGE=90°,
∴△AEG为等腰直角三角形.
(3)如图,连接AC,
∵四边形ABCD是正方形,
∴AC=AB=,
∵△AEG为等腰直角三角形,GF⊥AE,
∴GF=AF=EF=1,
∴AG=GE=,
∵AC2=AG2+GC2,
∴10=2+(EC+)2,
∴EC=(负根已经舍弃).
28.解:(1)∵四边形ABCD为正方形,
∴∠DAE=∠ABF=90°,AD=AB,
∵DE⊥AF,
∴∠DAH+∠ADE=90°,
∵∠DAH+∠BAF=90°,
∴∠ADE=∠BAF,
在△AED和△BFA中,
,
∴△AED≌△BFA(ASA).
(2)△ADM是等腰三角形,理由如下:
∵∠BAC=45°,AF平分∠BAC,
∴∠BAF=∠CAF=∠BAC=22.5°,
∴∠DAM=∠DAC+∠CAF=67.5°,
∴∠DMA=180°﹣∠DAM﹣∠ADM=180°﹣67.5°﹣45°=67.5°,
∴∠DAM=∠DMA,
∴△ADM是等腰三角形.
(3)∵∠ADE=∠BAF=22.5°,
∴∠CDG=∠ADC﹣∠ADE=67.5°,
∴∠DGC=180°﹣∠GCD﹣∠CDG=67.5°,
∴CG=CB,
∵AE∥CD,
∴∠AEG=∠CDG=67.5°,
∴AE=AG,
如图,作FK⊥AC于点K,设AG=AE=x,
∵AO=AG+OG=x+1,
∴AB=BC=AO=(x+1),AC=2AO=2(x+1),
∵△AED≌△BFA,
∴BF=AE=x,
∵AF平分∠BAC,
∴FK=BF=x,
∵S△ABF=AB?BF,S△ACF=AC?FK,
∴==,
又∵=,
∴==,
即=,
解得x=,
∴BE=AB﹣AE=(x+1)﹣x=2.
29.(1)证明:过点P作PG⊥BC于G,过点P作PH⊥DC于H,如图1.
∵四边形ABCD是正方形,PG⊥BC,PH⊥DC,
∴∠GPC=∠ACB=∠ACD=∠HPC=45°.
∴PG=PH,∠GPH=∠PGB=∠PHE=90°.
∵PE⊥PB,即∠BPE=90°,
∴∠BPG=90°﹣∠GPE=∠EPH.
在△PGB和△PHE中,
,
∴△PGB≌△PHE(ASA),
∴PB=PE.
(2)解:PF的长度不变.
连接BD,如图2.
∵四边形ABCD是正方形,
∴∠BOP=90°,
∵PE⊥PB,即∠BPE=90°,
∴∠PBO=90°﹣∠BPO=∠EPF,
∵EF⊥PC,即∠PFE=90°,
∴∠BOP=∠PFE,
在△BOP和△PFE中,
,
∴△BOP≌△PFE(AAS),
∴BO=PF.
∵四边形ABCD是正方形,
∴OB=OC,∠BOC=90°,
∴BC=OB.
∵BC=2,
∴OB=,
∴PF=OB=.
∴点P在运动过程中,PF的长度不变,值为.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
