北师大版数学九年级下册第三章圆9.弧长及扇形的面积课后练习(word版含答案)
文档属性
| 名称 | 北师大版数学九年级下册第三章圆9.弧长及扇形的面积课后练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 274.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 14:09:49 | ||
图片预览



文档简介
1141730011798300
第三章圆9.弧长及扇形的面积课后练习2020-2021学年下学期九年级下册初中数学北师大版
一、单选题(共12题 )
1.如图所示,点A,B,C对应的刻度分别为1,3,5,将线段 CA 绕点C按顺时针方向旋转,当点A首次落在矩形 BCDE 的边 BE 上时,记为点 A′ ,则此时线段 CA 扫过的图形的面积为(?? )
A.?43???????????????????????????????????????B.?6???????????????????????????????????????C.?43π???????????????????????????????????????D.?83π
2.如图,公园内有一个半径为18米的圆形草坪,从 A 地走到 B 地有观赏路(劣弧 AB )和便民路(线段 AB ).已知 A 、 B 是圆上的点, O 为圆心, ∠AOB=120° ,小强从 A 走到 B ,走便民路比走观赏路少走(?? )米.
A.?6π?63????????????????????????B.?6π?93????????????????????????C.?12π?93????????????????????????D.?12π?183
3.沪苏湖高铁在紧张施工中,现在南浔站已开始隧道挖掘作业,如图1,圆弧形混凝土管片是构成圆形隧道的重要部件,如图2,有一圆弧形混凝土管片放置在水平地面上,底部用两个完全相同的长方体木块固定,为估计隧洞开挖面的大小,甲、乙、丙三个小组对相关数据进行测量方案如下表,利用数据能够估算隧道外径大小的小组有(?? )
小组
测量内容
甲
HG , GN 的长
乙
AB , AD , BC 的长
丙
AB 的长,点 A 、 D 间距离,点 B 、 C 间的距离
A.?三组测量数据都不足???????????????????B.?一个小组???????????????????C.?两个小组???????????????????D.?三个组都可以
4.若圆锥的轴截面为等边三角形,则称此圆锥为正圆锥,则正圆锥侧面展开图的圆心角是(?? )
A.?90°?????????????????????????????????????B.?120°?????????????????????????????????????C.?150°?????????????????????????????????????D.?180°
5.如图,在扇形纸片 OAB 中, OA=10,∠AOB=36°,OB 在桌面内的直线l上.现将此扇形在直线l上按顺时针方向旋转(旋转过程中无滑动),当 OA 落在l上时,停止旋转.则点O所经过的路线长为(?? )
A.?13π??????????????????????????????????????B.?12π??????????????????????????????????????C.?11π??????????????????????????????????????D.?10π
6.如图,从一块半径为 8cm 的圆形铁皮上剪出一个圆心角是 60° 的扇形 ABC ,则此扇形围成的圆锥底面圆的半径为(??? )
A.?83???????????????????????????????????????B.?43???????????????????????????????????????C.?833???????????????????????????????????????D.?433
7.如图,将⊙O沿弦 AB 折叠, AB 恰好经过圆心O , 若⊙O的半径为6,则 AB 的长为(??? )
A.?4π?????????????????????????????????????????B.?π?????????????????????????????????????????C.?2π?????????????????????????????????????????D.?6π
8.半径为 2cm ,圆心角为 90° 的扇形的面积等于( ??)
A.?1cm2?????????????????????????????????B.?πcm2?????????????????????????????????C.?2πcm2?????????????????????????????????D.?4πcm2
9.一个扇形的半径为3cm,面积为 π?cm2 ,则此扇形的圆心角为(????? )
A.?30°???????????????????????????????????B.?40°???????????????????????????????????C.?80°???????????????????????????????????D.?120°
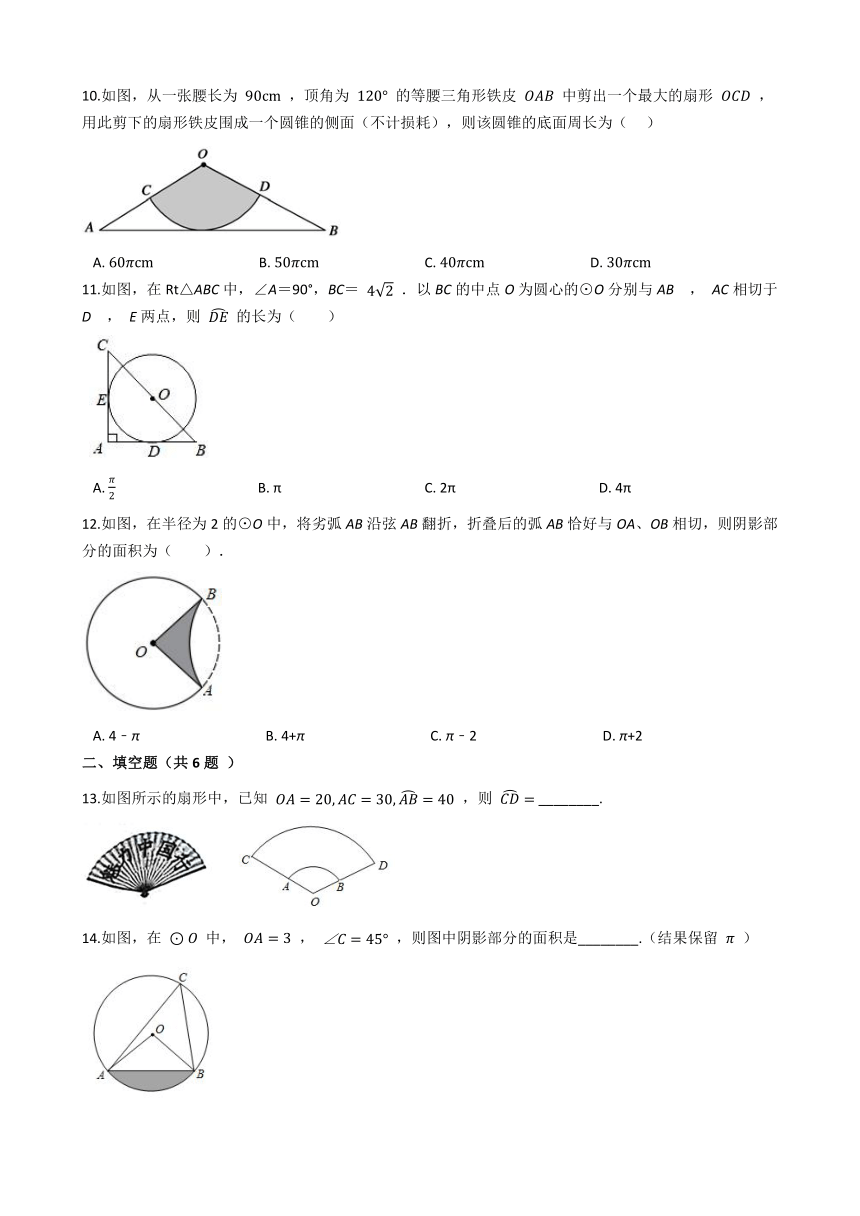
10.如图,从一张腰长为 90cm ,顶角为 120° 的等腰三角形铁皮 OAB 中剪出一个最大的扇形 OCD ,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面周长为(??? )
A.?60πcm??????????????????????????????B.?50πcm??????????????????????????????C.?40πcm??????????????????????????????D.?30πcm
11.如图,在Rt△ABC中,∠A=90°,BC= 42 .以BC的中点O为圆心的⊙O分别与AB , AC相切于D , E两点,则 DE 的长为( )
A.?π2?????????????????????????????????????????B.?π?????????????????????????????????????????C.?2π?????????????????????????????????????????D.?4π
12.如图,在半径为2的⊙O中,将劣弧AB沿弦AB翻折,折叠后的弧AB恰好与OA、OB相切,则阴影部分的面积为( ).
A.?4﹣π????????????????????????????????????B.?4+π????????????????????????????????????C.?π﹣2????????????????????????????????????D.?π+2
二、填空题(共6题 )
13.如图所示的扇形中,已知 OA=20,AC=30,AB=40 ,则 CD= ________.
14.如图,在 ⊙O 中, OA=3 , ∠C=45° ,则图中阴影部分的面积是________.(结果保留 π )
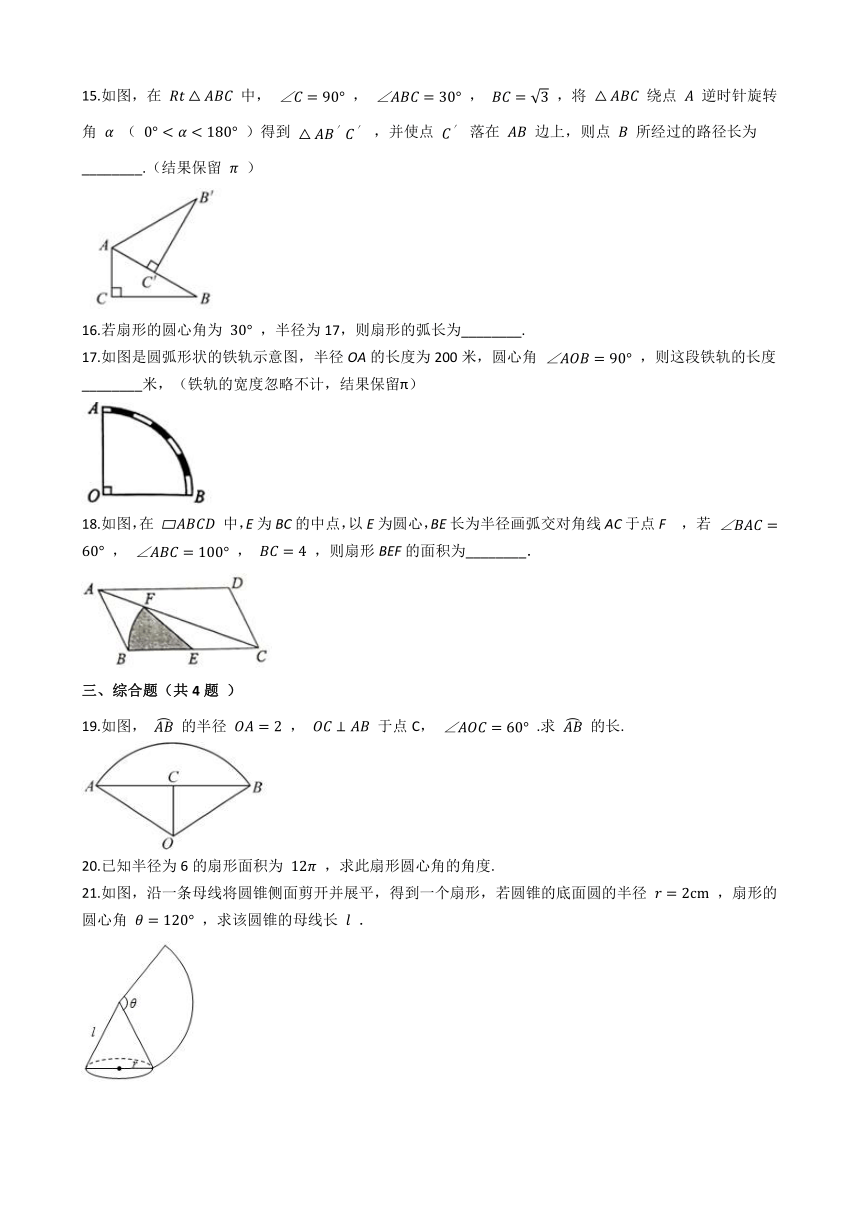
15.如图,在 Rt△ABC 中, ∠C=90° , ∠ABC=30° , BC=3 ,将 △ABC 绕点 A 逆时针旋转角 α ( 0°<α<180° )得到 △AB′C′ ,并使点 C′ 落在 AB 边上,则点 B 所经过的路径长为________.(结果保留 π )
16.若扇形的圆心角为 30° ,半径为17,则扇形的弧长为________.
17.如图是圆弧形状的铁轨示意图,半径OA的长度为200米,圆心角 ∠AOB=90° ,则这段铁轨的长度________米,(铁轨的宽度忽略不计,结果保留π)
18.如图,在 ?ABCD 中,E为BC的中点,以E为圆心,BE长为半径画弧交对角线AC于点F , 若 ∠BAC=60° , ∠ABC=100° , BC=4 ,则扇形BEF的面积为________.
三、综合题(共4题 )
19.如图, AB 的半径 OA=2 , OC⊥AB 于点C, ∠AOC=60° .求 AB 的长.
20.已知半径为6的扇形面积为 12π ,求此扇形圆心角的角度.
21.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 r=2cm ,扇形的圆心角 θ=120° ,求该圆锥的母线长 l .
22.如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,图中的三个扇形(即三个阴影部分)的面积之和是多少?弧长的和为多少?
答案解析部分
一、单选题
1.【答案】 D
【解析】【解答】解:由图可知:AC=A’C=4,BC=2,
∴ sin∠BA'C=BCA'C=24=12 ,
∴ ∠BA'C=30?,∠BCA'=60? ,
线段 CA 扫过的图形为扇形,此扇形的半径为 CA=4 ,
∴ S扇形ACA'=60?360?π×42=83π ,
故答案为:D.
【分析】由图可知:AC=A′C=4,BC=2,然后根据三角函数的概念可得tan∠BA′C的值,进而得到∠BA′C的度数,最后根据扇形面积公式进行计算.
2.【答案】 D
【解析】【解答】解:作OC⊥AB于C,如图,
则AC=BC,
∵OA=OB,
∴∠A=∠B= 12 (180°-∠AOB)=30°,
在Rt△AOC中,OC= 12 OA=9,
AC= 182?92=93 ,
∴AB=2AC= 183 ,
又∵ AB=120×π×18180 = 12π ,
∴走便民路比走观赏路少走 12π?183 米,
故答案为:D.
【分析】作OC⊥AB于C,由垂径定理可得AC=BC,由等边对等角和三角形内角和定理可得∠A=∠B=12(180°-∠AOB),在Rt△AOC中,用勾股定理可求得AC的值,再根据AB=2AC可求得AB的值,用弧长公式l=nπR180可求得弧AB的值,再求差即可求解.
3.【答案】 D
【解析】【解答】解:连接HM,则四边形HGNM是矩形,过点O作OK⊥GN,垂足为K,则OK⊥HM,垂足为 O′ ,如图,
∴四边形 HGKO′ 是矩形,
∴ KO′=HG
对于甲:可直接测量出HG,GN,
设外径为R,
则在 RtΔOO′M 中, OM2=OO′2+MO′2
∴ R2=(R?KO′)2+MO′2
∴ R2=(R?HG)2+(12GN)2
∵HG,GN已知,
∴ R2 可求,故甲组能够估算隧道外径大小;
对于乙:设外径为R,则内径为(R-AB)
设圆心角 ∠AOC=α ,则:
AD=πα(R?AB)180 ?, BC=παR180
∴ ADBC=R?ABR
∵ AD,BC,AB 已知
∴R可求,故乙组能够估算隧道外径大小;
对于丙:连接AD,BC,过点O作OK⊥BC,垂足为K,则OK⊥AD,垂足为 O′ ,如图,
设外径为R,则内径为(R-AB)
设圆心角 ∠AOC=α ,则: ∠BOK=∠AOO′=12∠α
∴ sinα2=AO′AO=BKBO
∴ 12ADOA=12BCBO ,即: 12ADR?AB=12BCR
∵AB,AD,BC已知,
∴R可求,故丙组能够估算隧道外径大小;
∴三个组都能够估算隧道外径大小.
故答案为:D.
【分析】根据垂径定理和勾股定理即可判断出甲;运用弧长公式可判断出乙;根据锐角的正弦值相等可判断丙.
4.【答案】 D
【解析】【解答】设正圆锥的底面半径是r,则母线长是2r,底面周长是2πr,
设正圆锥的侧面展开图的圆心角是n°,
则 2r?πr180 =2πr,
解得:n=180°.
故答案为:D.
【分析】本题要求学生理清圆锥底面半径、母线以及侧面展开图的圆心角之间的对应关系。
5.【答案】 B
【解析】【解答】解:点O经过的路线长
= 90π×10180+36π×10180+90π×10180
= 216×π×10180
=12π
?故答案为:B
【分析】点O所经过的路线是三段弧,一段是以点B为圆心,10为半径,圆心角为90°的弧,另一段是一条线段,和弧AB一样长的线段,最后一段是以点A为圆心,10为半径,圆心角为90°的弧,从而得出答案.
6.【答案】 D
【解析】【解答】解:如图,连接 BC ,并作 OD⊥BC 于点D .
∵ ∠BAC=60° ,
∴ ∠BOC=120° ,
∵OB=OC ,
∴ ∠OBD=30° , BD=CD=12BC ,
∴ BD=32OB=32×8=43 .
∴ BC=2BD=83 .
∵AB=AC ,
∴ △ABC 是等边三角形,
∴ AB=BC=83 ,
∴ BC=60π×2AB360=60π×2×83360=833π ,
∴设此扇形围成的圆锥底面圆的半径为r,
∴ 2πr=833π ,
∴ r=433 .
故答案为:D.
【分析】根据题意,由同弧所对的圆周角和圆心角的性质,结合题意,证明△ABC为等边三角形,继而由等边三角形的性质,结合弧长公式,求出半径r。
7.【答案】 A
【解析】【解答】解:连接OA、OB , 作OC⊥AB于C ,
由题意得,OC= 12 OA ,
∴sin∠OAC= OCOA = 12 ,
∴∠OAC=30°,
∵OA=OB ,
∴∠OBA=∠OAC=30°,
∴∠AOB=120°,
∴ AB=nπr180=120π×6180=4π ,
故答案为:A.
【分析】连接OA、OB , 作OC⊥AB于C , 由题意得,OC= 12 OA , 根据锐角三角函数求得∠OAC=30°,再根据等腰三角形的性质,三角形内角和定理求出∠AOB=120°,最后利用弧长公式计算即可。
8.【答案】 B
【解析】【解答】扇形的面积为: 90×π×22360=90×π×4360=π(cm2)
故答案为:B
【分析】假设出扇形半径,再表示出半圆面积,以及扇形面积,进而即可表示出两部分P、Q面积相等,连接AB、OD,根据两半圆的直径相等可知∠AOD=∠BOD=45? , 故可得出绿色部分的面积,利用阴影部分的面积=扇形面积-半圆-绿色面积即可。
9.【答案】 B
【解析】【解答】设扇形的圆心角为x°,根据题意可得:
S=xπ32360=π ,
解得 x=40 ,即扇形的圆心角为40°.
故答案为:B.
【分析】利用扇形的面积公式列出方程求解即可。
10.【答案】 D
【解析】【解答】解:过 O 作 OE⊥AB 于E ,
∵ OA=OB=90cm , ∠AOB=120° ,
∴ ∠A=∠B=30° ,
∴ OE=OA=45cm ,
∴弧CD的长 =120×π×45180=30π ,
故答案为:D.
【分析】根据等腰三角形的性质得到OE的长,再利用弧长公式计算出弧CD的长,根据圆锥的侧面展开图为扇形,这个扇形的弧长等于圆锥的底面的周长即可得出。
11.【答案】 B
【解析】【解答】解:连接OD、OE、OA , 如图,
∵⊙O分别与AB , AC相切于D , E两点,
∴OD⊥AB , OE⊥AC ,
而∠A=90°,OD=OE ,
∴四边形ADOE为正方形,
∴∠DOE=90°,
∵O点为BC的中点,
∴OA= 12 BC= 12 ×4 2 =2 2 ,
∴OD= 22 OA= 22 ×2 2 =2,
∴ DE 的长= 90π×2180 =π.
故答案为:B .
【分析】连接OD、OE、OA , 如图,根据切线的性质得OD⊥AB , OE⊥AC , 则可判断四边形ADOE为正方形,所以∠DOE=90°,在根据斜边上的中线性质得到OA= 12 BC= 12 ×4 2 =2 2 ,接着根据正方形的性质计算出OD的长,在根据弧长公式计算即可。
12.【答案】 A
【解析】【解答】解:如图,作O点关于AB的对称点O′,连接O′A、O′B ,
∵OA=OB=O′A=O′B ,
∴四边形OAO′B为菱形,
∵折叠后的 AB 与OA、OB相切,
∴O′A⊥OA , O′B⊥OB ,
∴四边形OAO′B为正方形,
∴∠AOB=∠A O′B=90°,
∴阴影部分的面积=正方形OAO′B面积-扇形AO′B面积=22- 14 π×22=4-π
故答案为:A.
【分析】作O点关于AB的对称点O′,连接O′A、O′B,可证明四边形OAO′B为正方形,可得∠AOB=∠A O′B=90°,根据阴影部分的面积=正方形OAO′B面积-扇形AO′B面积,利用正方形的面积、扇形的面积公式计算即可.
二、填空题
13.【答案】 100
【解析】【解答】解:设扇形圆心角度数为n°,
∵ OA=20,AB=40 ,
∴在扇形 AOB 中, AB=2π·OA·n360 ,
解得: n=360π ,
∴在扇形 COD 中, OC=OA+AC=20+30=50 ,
CD=2π·OC·n360=2π×50×360π360=100
故答案为:100.
【分析】先求出扇形圆心角度数360π , 再求出OC=OA+AC=50,利用弧长公式计算即可.
14.【答案】 9π4?92
【解析】【解答】解:∵ ∠C=45° ,
∴ ∠AOB=90° ,
∴S阴影=S扇形AOB- S△AOB
=90×π×32360?12×3×3
=9π4?92 ,
故答案为: 9π4?92 .
【分析】利用圆周角定理求出∠AOB的度数,再根据S阴影=S扇形AOB-S△AOB , 利用扇形的面积公式和三角形的面积公式可求解.
?
15.【答案】 23π
【解析】【解答】解:∵ ∠C=90° , ∠ABC=30° , BC=3 ,
∴AB=2AC,
设AC=x,则AB=2x,由勾股定理得:
x2+(3)2=(2x)2 ,
解得:x=1,
则:AC=1,AB=2,
∵将 △ABC 绕点 A 逆时针旋转角 α ( 0°<α<180° )得到 △AB′C' ,且点 C′ 落在 AB 边上,
∴旋转角为60°,
∴∠ BAB' =60°,
∴点 B 所经过的路径长为: nπr180=60π180×AB=π3×2=2π3 ,
故答案为: 23π .
【分析】利用已知条件可证得AB=2AC,设AC=x,则AB=2x,利用勾股定理建立关于x的方程,解方程求出x的值,可得到AC,AB的长;再利用旋转的性质可求出∠BAB'的度数;然后利用弧长公式可求解.
16.【答案】 176π
【解析】【解答】∵扇形的圆心角为 30° ,半径为17,
∴扇形的弧长= 30π×17180 = 176π .
故答案为: 176π
【分析】把数据直接代入扇形的弧长公式l=nπr180计算即可.
17.【答案】 100π
【解析】【解答】解:由题意可知,铁轨的长度为劣弧AB的长度 =nπr180?=90?180?×π×200=100π ,
故答案为: 100π .
【分析】利用弧长公式计算求解即可。
18.【答案】 4π9
【解析】【解答】解:∵ ∠BAC=60° , ∠ABC=100° ,
∴ ∠ACB=20° ,
∵E为BC的中点,EB、EF为半径,
∴ ∠EFC=∠ECF=20° ,
∴ ∠BEF=40° ,
∵ BC=4 ,
∴ BE=2 ,
∴扇形BEF的面积 =40π×22360=4π9 .
【分析】根据三角形内角和定理求出∠ACB=20° , 根据三角形的外角的性质求出∠BEF=40° , 根据扇形面积公式计算出来即可。
三、解答题
19.【答案】 解:∵OC⊥AB,∠AOC=60°,
∴∠AOB=120°.
∵OA=2,
∴ AB 的长为:120π×2180=4π3.
【解析】【分析】首先由垂径定理结合已知条件可得∠AOB=120°,然后根据弧长公式:nπr180计算即可.
20.【答案】 解:∵ r=6 , S扇形=12π ,
∴ S扇形=nπr2360=12π ,
解得: n=120 ,
∴ 扇形圆心角的角度为 120° .
【解析】【分析】直接根据扇形的面积公式列等式即可扇形圆心角的角度.
21.【答案】 解:圆锥的底面周长 =2π×2=4π(cm) ,
由题意可得 120?π?l180=4π ,解得 l=6 ,
所以该圆锥的母线长为 6cm
【解析】【分析】根据题意求出 ,最后计算求解即可。
22.【答案】 解:三个扇形的半径都是2cm,根据扇形的面积公式S= nπr2360 ,
因而三个扇形的面积的和就是:三个圆心角的和× πr2360 ,
而三个圆心角的和是180°,
∴图中的三个扇形(即三个阴影部分)的面积之和为180× 22π360 =2πcm2.
弧长之和即为圆心角为180°,半径为2cm半圆的弧长,即 180×2π180=2π cm.
【解析】【分析】观察图形可知三角形的内角和为180°,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,三个阴影部分拼在一起,就是求圆心角为180°,半径为2cm的扇形的面积和扇形的弧长,然后利用扇形的弧长和面积公式可求解.
第三章圆9.弧长及扇形的面积课后练习2020-2021学年下学期九年级下册初中数学北师大版
一、单选题(共12题 )
1.如图所示,点A,B,C对应的刻度分别为1,3,5,将线段 CA 绕点C按顺时针方向旋转,当点A首次落在矩形 BCDE 的边 BE 上时,记为点 A′ ,则此时线段 CA 扫过的图形的面积为(?? )
A.?43???????????????????????????????????????B.?6???????????????????????????????????????C.?43π???????????????????????????????????????D.?83π
2.如图,公园内有一个半径为18米的圆形草坪,从 A 地走到 B 地有观赏路(劣弧 AB )和便民路(线段 AB ).已知 A 、 B 是圆上的点, O 为圆心, ∠AOB=120° ,小强从 A 走到 B ,走便民路比走观赏路少走(?? )米.
A.?6π?63????????????????????????B.?6π?93????????????????????????C.?12π?93????????????????????????D.?12π?183
3.沪苏湖高铁在紧张施工中,现在南浔站已开始隧道挖掘作业,如图1,圆弧形混凝土管片是构成圆形隧道的重要部件,如图2,有一圆弧形混凝土管片放置在水平地面上,底部用两个完全相同的长方体木块固定,为估计隧洞开挖面的大小,甲、乙、丙三个小组对相关数据进行测量方案如下表,利用数据能够估算隧道外径大小的小组有(?? )
小组
测量内容
甲
HG , GN 的长
乙
AB , AD , BC 的长
丙
AB 的长,点 A 、 D 间距离,点 B 、 C 间的距离
A.?三组测量数据都不足???????????????????B.?一个小组???????????????????C.?两个小组???????????????????D.?三个组都可以
4.若圆锥的轴截面为等边三角形,则称此圆锥为正圆锥,则正圆锥侧面展开图的圆心角是(?? )
A.?90°?????????????????????????????????????B.?120°?????????????????????????????????????C.?150°?????????????????????????????????????D.?180°
5.如图,在扇形纸片 OAB 中, OA=10,∠AOB=36°,OB 在桌面内的直线l上.现将此扇形在直线l上按顺时针方向旋转(旋转过程中无滑动),当 OA 落在l上时,停止旋转.则点O所经过的路线长为(?? )
A.?13π??????????????????????????????????????B.?12π??????????????????????????????????????C.?11π??????????????????????????????????????D.?10π
6.如图,从一块半径为 8cm 的圆形铁皮上剪出一个圆心角是 60° 的扇形 ABC ,则此扇形围成的圆锥底面圆的半径为(??? )
A.?83???????????????????????????????????????B.?43???????????????????????????????????????C.?833???????????????????????????????????????D.?433
7.如图,将⊙O沿弦 AB 折叠, AB 恰好经过圆心O , 若⊙O的半径为6,则 AB 的长为(??? )
A.?4π?????????????????????????????????????????B.?π?????????????????????????????????????????C.?2π?????????????????????????????????????????D.?6π
8.半径为 2cm ,圆心角为 90° 的扇形的面积等于( ??)
A.?1cm2?????????????????????????????????B.?πcm2?????????????????????????????????C.?2πcm2?????????????????????????????????D.?4πcm2
9.一个扇形的半径为3cm,面积为 π?cm2 ,则此扇形的圆心角为(????? )
A.?30°???????????????????????????????????B.?40°???????????????????????????????????C.?80°???????????????????????????????????D.?120°
10.如图,从一张腰长为 90cm ,顶角为 120° 的等腰三角形铁皮 OAB 中剪出一个最大的扇形 OCD ,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面周长为(??? )
A.?60πcm??????????????????????????????B.?50πcm??????????????????????????????C.?40πcm??????????????????????????????D.?30πcm
11.如图,在Rt△ABC中,∠A=90°,BC= 42 .以BC的中点O为圆心的⊙O分别与AB , AC相切于D , E两点,则 DE 的长为( )
A.?π2?????????????????????????????????????????B.?π?????????????????????????????????????????C.?2π?????????????????????????????????????????D.?4π
12.如图,在半径为2的⊙O中,将劣弧AB沿弦AB翻折,折叠后的弧AB恰好与OA、OB相切,则阴影部分的面积为( ).
A.?4﹣π????????????????????????????????????B.?4+π????????????????????????????????????C.?π﹣2????????????????????????????????????D.?π+2
二、填空题(共6题 )
13.如图所示的扇形中,已知 OA=20,AC=30,AB=40 ,则 CD= ________.
14.如图,在 ⊙O 中, OA=3 , ∠C=45° ,则图中阴影部分的面积是________.(结果保留 π )
15.如图,在 Rt△ABC 中, ∠C=90° , ∠ABC=30° , BC=3 ,将 △ABC 绕点 A 逆时针旋转角 α ( 0°<α<180° )得到 △AB′C′ ,并使点 C′ 落在 AB 边上,则点 B 所经过的路径长为________.(结果保留 π )
16.若扇形的圆心角为 30° ,半径为17,则扇形的弧长为________.
17.如图是圆弧形状的铁轨示意图,半径OA的长度为200米,圆心角 ∠AOB=90° ,则这段铁轨的长度________米,(铁轨的宽度忽略不计,结果保留π)
18.如图,在 ?ABCD 中,E为BC的中点,以E为圆心,BE长为半径画弧交对角线AC于点F , 若 ∠BAC=60° , ∠ABC=100° , BC=4 ,则扇形BEF的面积为________.
三、综合题(共4题 )
19.如图, AB 的半径 OA=2 , OC⊥AB 于点C, ∠AOC=60° .求 AB 的长.
20.已知半径为6的扇形面积为 12π ,求此扇形圆心角的角度.
21.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 r=2cm ,扇形的圆心角 θ=120° ,求该圆锥的母线长 l .
22.如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,图中的三个扇形(即三个阴影部分)的面积之和是多少?弧长的和为多少?
答案解析部分
一、单选题
1.【答案】 D
【解析】【解答】解:由图可知:AC=A’C=4,BC=2,
∴ sin∠BA'C=BCA'C=24=12 ,
∴ ∠BA'C=30?,∠BCA'=60? ,
线段 CA 扫过的图形为扇形,此扇形的半径为 CA=4 ,
∴ S扇形ACA'=60?360?π×42=83π ,
故答案为:D.
【分析】由图可知:AC=A′C=4,BC=2,然后根据三角函数的概念可得tan∠BA′C的值,进而得到∠BA′C的度数,最后根据扇形面积公式进行计算.
2.【答案】 D
【解析】【解答】解:作OC⊥AB于C,如图,
则AC=BC,
∵OA=OB,
∴∠A=∠B= 12 (180°-∠AOB)=30°,
在Rt△AOC中,OC= 12 OA=9,
AC= 182?92=93 ,
∴AB=2AC= 183 ,
又∵ AB=120×π×18180 = 12π ,
∴走便民路比走观赏路少走 12π?183 米,
故答案为:D.
【分析】作OC⊥AB于C,由垂径定理可得AC=BC,由等边对等角和三角形内角和定理可得∠A=∠B=12(180°-∠AOB),在Rt△AOC中,用勾股定理可求得AC的值,再根据AB=2AC可求得AB的值,用弧长公式l=nπR180可求得弧AB的值,再求差即可求解.
3.【答案】 D
【解析】【解答】解:连接HM,则四边形HGNM是矩形,过点O作OK⊥GN,垂足为K,则OK⊥HM,垂足为 O′ ,如图,
∴四边形 HGKO′ 是矩形,
∴ KO′=HG
对于甲:可直接测量出HG,GN,
设外径为R,
则在 RtΔOO′M 中, OM2=OO′2+MO′2
∴ R2=(R?KO′)2+MO′2
∴ R2=(R?HG)2+(12GN)2
∵HG,GN已知,
∴ R2 可求,故甲组能够估算隧道外径大小;
对于乙:设外径为R,则内径为(R-AB)
设圆心角 ∠AOC=α ,则:
AD=πα(R?AB)180 ?, BC=παR180
∴ ADBC=R?ABR
∵ AD,BC,AB 已知
∴R可求,故乙组能够估算隧道外径大小;
对于丙:连接AD,BC,过点O作OK⊥BC,垂足为K,则OK⊥AD,垂足为 O′ ,如图,
设外径为R,则内径为(R-AB)
设圆心角 ∠AOC=α ,则: ∠BOK=∠AOO′=12∠α
∴ sinα2=AO′AO=BKBO
∴ 12ADOA=12BCBO ,即: 12ADR?AB=12BCR
∵AB,AD,BC已知,
∴R可求,故丙组能够估算隧道外径大小;
∴三个组都能够估算隧道外径大小.
故答案为:D.
【分析】根据垂径定理和勾股定理即可判断出甲;运用弧长公式可判断出乙;根据锐角的正弦值相等可判断丙.
4.【答案】 D
【解析】【解答】设正圆锥的底面半径是r,则母线长是2r,底面周长是2πr,
设正圆锥的侧面展开图的圆心角是n°,
则 2r?πr180 =2πr,
解得:n=180°.
故答案为:D.
【分析】本题要求学生理清圆锥底面半径、母线以及侧面展开图的圆心角之间的对应关系。
5.【答案】 B
【解析】【解答】解:点O经过的路线长
= 90π×10180+36π×10180+90π×10180
= 216×π×10180
=12π
?故答案为:B
【分析】点O所经过的路线是三段弧,一段是以点B为圆心,10为半径,圆心角为90°的弧,另一段是一条线段,和弧AB一样长的线段,最后一段是以点A为圆心,10为半径,圆心角为90°的弧,从而得出答案.
6.【答案】 D
【解析】【解答】解:如图,连接 BC ,并作 OD⊥BC 于点D .
∵ ∠BAC=60° ,
∴ ∠BOC=120° ,
∵OB=OC ,
∴ ∠OBD=30° , BD=CD=12BC ,
∴ BD=32OB=32×8=43 .
∴ BC=2BD=83 .
∵AB=AC ,
∴ △ABC 是等边三角形,
∴ AB=BC=83 ,
∴ BC=60π×2AB360=60π×2×83360=833π ,
∴设此扇形围成的圆锥底面圆的半径为r,
∴ 2πr=833π ,
∴ r=433 .
故答案为:D.
【分析】根据题意,由同弧所对的圆周角和圆心角的性质,结合题意,证明△ABC为等边三角形,继而由等边三角形的性质,结合弧长公式,求出半径r。
7.【答案】 A
【解析】【解答】解:连接OA、OB , 作OC⊥AB于C ,
由题意得,OC= 12 OA ,
∴sin∠OAC= OCOA = 12 ,
∴∠OAC=30°,
∵OA=OB ,
∴∠OBA=∠OAC=30°,
∴∠AOB=120°,
∴ AB=nπr180=120π×6180=4π ,
故答案为:A.
【分析】连接OA、OB , 作OC⊥AB于C , 由题意得,OC= 12 OA , 根据锐角三角函数求得∠OAC=30°,再根据等腰三角形的性质,三角形内角和定理求出∠AOB=120°,最后利用弧长公式计算即可。
8.【答案】 B
【解析】【解答】扇形的面积为: 90×π×22360=90×π×4360=π(cm2)
故答案为:B
【分析】假设出扇形半径,再表示出半圆面积,以及扇形面积,进而即可表示出两部分P、Q面积相等,连接AB、OD,根据两半圆的直径相等可知∠AOD=∠BOD=45? , 故可得出绿色部分的面积,利用阴影部分的面积=扇形面积-半圆-绿色面积即可。
9.【答案】 B
【解析】【解答】设扇形的圆心角为x°,根据题意可得:
S=xπ32360=π ,
解得 x=40 ,即扇形的圆心角为40°.
故答案为:B.
【分析】利用扇形的面积公式列出方程求解即可。
10.【答案】 D
【解析】【解答】解:过 O 作 OE⊥AB 于E ,
∵ OA=OB=90cm , ∠AOB=120° ,
∴ ∠A=∠B=30° ,
∴ OE=OA=45cm ,
∴弧CD的长 =120×π×45180=30π ,
故答案为:D.
【分析】根据等腰三角形的性质得到OE的长,再利用弧长公式计算出弧CD的长,根据圆锥的侧面展开图为扇形,这个扇形的弧长等于圆锥的底面的周长即可得出。
11.【答案】 B
【解析】【解答】解:连接OD、OE、OA , 如图,
∵⊙O分别与AB , AC相切于D , E两点,
∴OD⊥AB , OE⊥AC ,
而∠A=90°,OD=OE ,
∴四边形ADOE为正方形,
∴∠DOE=90°,
∵O点为BC的中点,
∴OA= 12 BC= 12 ×4 2 =2 2 ,
∴OD= 22 OA= 22 ×2 2 =2,
∴ DE 的长= 90π×2180 =π.
故答案为:B .
【分析】连接OD、OE、OA , 如图,根据切线的性质得OD⊥AB , OE⊥AC , 则可判断四边形ADOE为正方形,所以∠DOE=90°,在根据斜边上的中线性质得到OA= 12 BC= 12 ×4 2 =2 2 ,接着根据正方形的性质计算出OD的长,在根据弧长公式计算即可。
12.【答案】 A
【解析】【解答】解:如图,作O点关于AB的对称点O′,连接O′A、O′B ,
∵OA=OB=O′A=O′B ,
∴四边形OAO′B为菱形,
∵折叠后的 AB 与OA、OB相切,
∴O′A⊥OA , O′B⊥OB ,
∴四边形OAO′B为正方形,
∴∠AOB=∠A O′B=90°,
∴阴影部分的面积=正方形OAO′B面积-扇形AO′B面积=22- 14 π×22=4-π
故答案为:A.
【分析】作O点关于AB的对称点O′,连接O′A、O′B,可证明四边形OAO′B为正方形,可得∠AOB=∠A O′B=90°,根据阴影部分的面积=正方形OAO′B面积-扇形AO′B面积,利用正方形的面积、扇形的面积公式计算即可.
二、填空题
13.【答案】 100
【解析】【解答】解:设扇形圆心角度数为n°,
∵ OA=20,AB=40 ,
∴在扇形 AOB 中, AB=2π·OA·n360 ,
解得: n=360π ,
∴在扇形 COD 中, OC=OA+AC=20+30=50 ,
CD=2π·OC·n360=2π×50×360π360=100
故答案为:100.
【分析】先求出扇形圆心角度数360π , 再求出OC=OA+AC=50,利用弧长公式计算即可.
14.【答案】 9π4?92
【解析】【解答】解:∵ ∠C=45° ,
∴ ∠AOB=90° ,
∴S阴影=S扇形AOB- S△AOB
=90×π×32360?12×3×3
=9π4?92 ,
故答案为: 9π4?92 .
【分析】利用圆周角定理求出∠AOB的度数,再根据S阴影=S扇形AOB-S△AOB , 利用扇形的面积公式和三角形的面积公式可求解.
?
15.【答案】 23π
【解析】【解答】解:∵ ∠C=90° , ∠ABC=30° , BC=3 ,
∴AB=2AC,
设AC=x,则AB=2x,由勾股定理得:
x2+(3)2=(2x)2 ,
解得:x=1,
则:AC=1,AB=2,
∵将 △ABC 绕点 A 逆时针旋转角 α ( 0°<α<180° )得到 △AB′C' ,且点 C′ 落在 AB 边上,
∴旋转角为60°,
∴∠ BAB' =60°,
∴点 B 所经过的路径长为: nπr180=60π180×AB=π3×2=2π3 ,
故答案为: 23π .
【分析】利用已知条件可证得AB=2AC,设AC=x,则AB=2x,利用勾股定理建立关于x的方程,解方程求出x的值,可得到AC,AB的长;再利用旋转的性质可求出∠BAB'的度数;然后利用弧长公式可求解.
16.【答案】 176π
【解析】【解答】∵扇形的圆心角为 30° ,半径为17,
∴扇形的弧长= 30π×17180 = 176π .
故答案为: 176π
【分析】把数据直接代入扇形的弧长公式l=nπr180计算即可.
17.【答案】 100π
【解析】【解答】解:由题意可知,铁轨的长度为劣弧AB的长度 =nπr180?=90?180?×π×200=100π ,
故答案为: 100π .
【分析】利用弧长公式计算求解即可。
18.【答案】 4π9
【解析】【解答】解:∵ ∠BAC=60° , ∠ABC=100° ,
∴ ∠ACB=20° ,
∵E为BC的中点,EB、EF为半径,
∴ ∠EFC=∠ECF=20° ,
∴ ∠BEF=40° ,
∵ BC=4 ,
∴ BE=2 ,
∴扇形BEF的面积 =40π×22360=4π9 .
【分析】根据三角形内角和定理求出∠ACB=20° , 根据三角形的外角的性质求出∠BEF=40° , 根据扇形面积公式计算出来即可。
三、解答题
19.【答案】 解:∵OC⊥AB,∠AOC=60°,
∴∠AOB=120°.
∵OA=2,
∴ AB 的长为:120π×2180=4π3.
【解析】【分析】首先由垂径定理结合已知条件可得∠AOB=120°,然后根据弧长公式:nπr180计算即可.
20.【答案】 解:∵ r=6 , S扇形=12π ,
∴ S扇形=nπr2360=12π ,
解得: n=120 ,
∴ 扇形圆心角的角度为 120° .
【解析】【分析】直接根据扇形的面积公式列等式即可扇形圆心角的角度.
21.【答案】 解:圆锥的底面周长 =2π×2=4π(cm) ,
由题意可得 120?π?l180=4π ,解得 l=6 ,
所以该圆锥的母线长为 6cm
【解析】【分析】根据题意求出 ,最后计算求解即可。
22.【答案】 解:三个扇形的半径都是2cm,根据扇形的面积公式S= nπr2360 ,
因而三个扇形的面积的和就是:三个圆心角的和× πr2360 ,
而三个圆心角的和是180°,
∴图中的三个扇形(即三个阴影部分)的面积之和为180× 22π360 =2πcm2.
弧长之和即为圆心角为180°,半径为2cm半圆的弧长,即 180×2π180=2π cm.
【解析】【分析】观察图形可知三角形的内角和为180°,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,三个阴影部分拼在一起,就是求圆心角为180°,半径为2cm的扇形的面积和扇形的弧长,然后利用扇形的弧长和面积公式可求解.
