北师大版九年级数学上册第一章特殊平行四边形1.2.1矩形的判定同步练习(word版含答案)
文档属性
| 名称 | 北师大版九年级数学上册第一章特殊平行四边形1.2.1矩形的判定同步练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 269.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 00:00:00 | ||
图片预览



文档简介
1.2.1矩形的判定同步练习
一.选择题(共7小题)
1.如图,D、E、F分别是△ABC各边中点,则以下说法错误的是( )
397764068580A.△BDE和△DCF的面积相等
B.四边形AEDF是平行四边形
C.若AB=BC,则四边形AEDF是菱形
D.若∠A=90°,则四边形AEDF是矩形
2.下列说法正确的是( )
A.有一组对角是直角的四边形一定是矩形
B.一条对角线被另一条对角线垂直平分的四边形是菱形
C.对角互补的平行四边形是矩形
D.对角线相等的四边形是矩形
3.如图,在△ABC中,AB=AC,AD⊥BC于点D,AE是∠BAC的外角的平分线,DE∥AB交AE于点E,则四边形ADCE的形状是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
4.如图,在平行四边形ABCD中,M、N是BD上两点,BM=DN,连接AM、MC、CN、NA,添加一个条件,使四边形AMCN是矩形,这个条件是( )
A.OM=AC B.MB=MO C.BD⊥AC D.∠AMB=∠CND
31623007620099060076200
第3题 第4题
5.在?ABCD中,AC,BD交于点O,设∠DBC=α°,∠BOC=β°,若β关于α的函数解析式是β=180﹣2α(0<α<90),则下列说法正确的是( )
A.BO=BC B.OC=BC
C.四边形ABCD是菱形 D.四边形ABCD是矩形
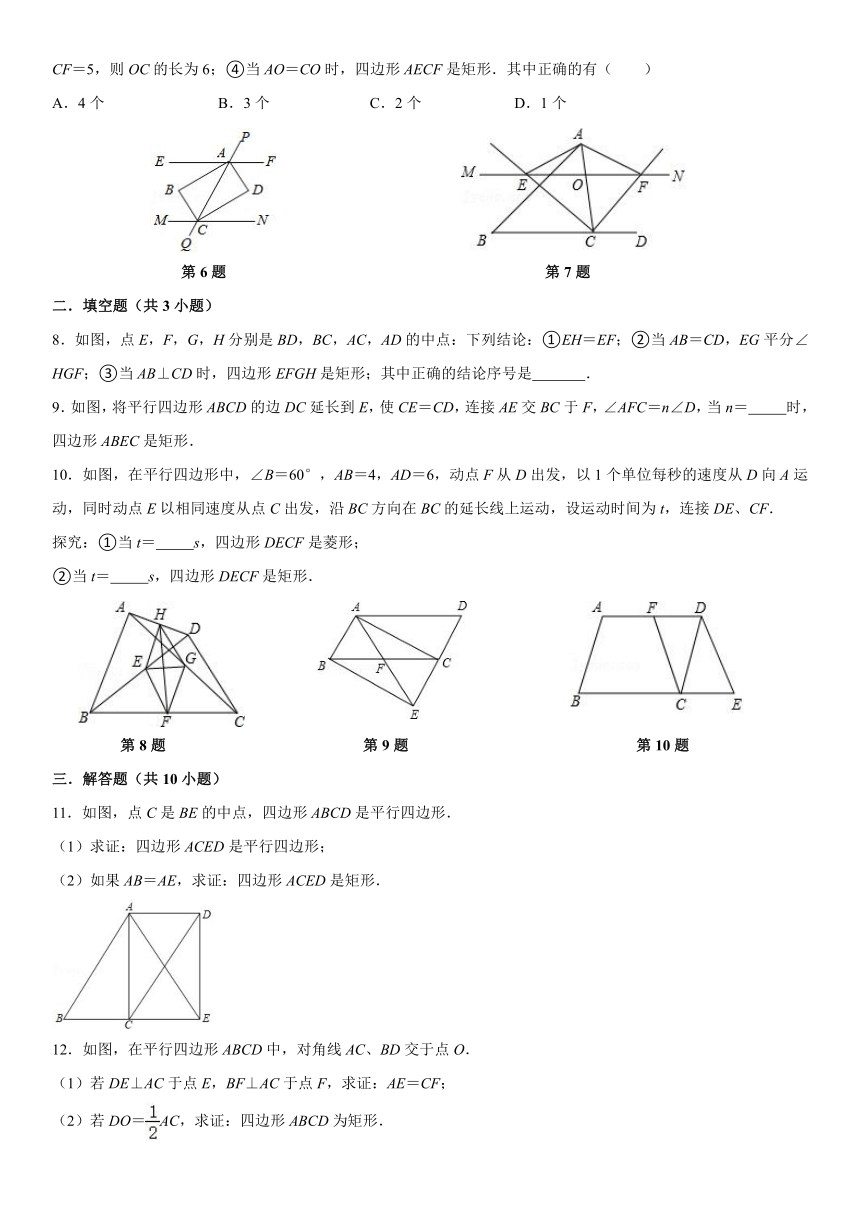
6.如图,直线EF∥MN,PQ交EF,MN于A,C两点,AB,CB,CD,AD分别是∠EAC,∠MCA,∠ACN,∠CAF的角平分线,则四边形ABCD是( )
A.菱形 B.平行四边形 C.矩形 D.不能确定
7.如图,在锐角△ABC中,延长BC到点D,点O是AC边上的一个动点,过点O作直线MN∥BC,MN分别交∠ACB、∠ACD的平分线于E,F两点,连接AE、AF,在下列结论中:①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
86868076200359664076200
第6题 第7题
二.填空题(共3小题)
8.如图,点E,F,G,H分别是BD,BC,AC,AD的中点:下列结论:①EH=EF;②当AB=CD,EG平分∠HGF;③当AB⊥CD时,四边形EFGH是矩形;其中正确的结论序号是 .
9.如图,将平行四边形ABCD的边DC延长到E,使CE=CD,连接AE交BC于F,∠AFC=n∠D,当n= 时,四边形ABEC是矩形.
10.如图,在平行四边形中,∠B=60°,AB=4,AD=6,动点F从D出发,以1个单位每秒的速度从D向A运动,同时动点E以相同速度从点C出发,沿BC方向在BC的延长线上运动,设运动时间为t,连接DE、CF.
探究:①当t= s,四边形DECF是菱形;
②当t= s,四边形DECF是矩形.
23317207620023622076200455676076200
第8题 第9题 第10题
三.解答题(共10小题)
11.如图,点C是BE的中点,四边形ABCD是平行四边形.
(1)求证:四边形ACED是平行四边形;
(2)如果AB=AE,求证:四边形ACED是矩形.
12.如图,在平行四边形ABCD中,对角线AC、BD交于点O.
(1)若DE⊥AC于点E,BF⊥AC于点F,求证:AE=CF;
(2)若DO=AC,求证:四边形ABCD为矩形.
13.如图,在△ABC中,∠ACB=90°,D点是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.
(1)求∠CFD的度数;
(2)求证:四边形FDEC是矩形.
14.如图,在等边△ABC中,点D是AC的中点,点F是BC的中点,以BD为边作等边△BDE,连接点A、E.求证:四边形AEBF为矩形.
15.如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.
(1)求证:△AFE≌△DFB;
(2)求证:四边形ADCE是平行四边形;
(3)当AB、AC之间满足什么条件时,四边形ADCE是矩形.
16.如图,在?ABCD中,点E是AD的中点,连接BE,BE、CD的延长线相交于点F,连接AF、BD.
(1)求证:四边形ABDF是平行四边形;
(2)当∠C与∠BED满足条件 时,四边形ABDF是矩形.
17.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当线段AB与线段AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
18.如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;
19.如图,△ABC的中线AD、BE、CF相交于点G,H、I分别是BG、CG的中点.
(1) 是△ABC的中位线,EF与BC位置关系是 、数量关系是 ; 是△GBC的中位线,HI与BC位置关系是 、数量关系是 ;
(2)求证:四边形EFHI是平行四边形;
(3)当AD与BC满足条件 时,四边形EFHI是矩形.(直接写出结论)当AD与BC满足条件 时,四边形EFHI是菱形.(直接写出结论)
20.已知:如图,AC、BD相交于点O,且点O是AC、BD的中点,点E在四边形ABCD的形外,且∠AEC=∠BED=90°.求证:四边形ABCD是矩形.
1.2.1矩形的判定同步练习
参考答案与试题解析
一.选择题(共7小题)
1.如图,D、E、F分别是△ABC各边中点,则以下说法错误的是( )
A.△BDE和△DCF的面积相等
B.四边形AEDF是平行四边形
C.若AB=BC,则四边形AEDF是菱形
D.若∠A=90°,则四边形AEDF是矩形
【解答】解:A.连接EF,
∵D、E、F分别是△ABC各边中点,
∴EF∥BC,BD=CD,
设EF和BC间的距离为h,
∴S△BDE=BD?h,S△DCE=CD?h,
∴S△BDE=S△DCE,
故本选项不符合题意;
B.∵D、E、F分别是△ABC各边中点,
∴DE∥AC,DF∥AB,
∴DE∥AF,DF∥AE,
∴四边形AEDF是平行四边形,
故本选项不符合题意;
C.∵D、E、F分别是△ABC各边中点,
∴EF=BC,DF=AB,
若AB=BC,则FE=DF,
∴四边形AEDF不一定是菱形,
故本选项符合题意;
D.∵四边形AEDF是平行四边形,
∴若∠A=90°,则四边形AEDF是矩形,
故本选项不符合题意;
故选:C.
2.下列说法正确的是( )
A.有一组对角是直角的四边形一定是矩形
B.一条对角线被另一条对角线垂直平分的四边形是菱形
C.对角互补的平行四边形是矩形
D.对角线相等的四边形是矩形
【解答】解:∵有一组对角是直角的四边形不一定是矩形,
∴选项A不正确;
∵两条对角线互相垂直平分的四边形是菱形,
∴选项B不正确;
∵对角互补的平行四边形一定是矩形,
∴选项C正确;
∵对角线相等的平行四边形是矩形,
∴选项D错误;
故选:C.
3.如图,在△ABC中,AB=AC,AD⊥BC于点D,AE是∠BAC的外角的平分线,DE∥AB交AE于点E,则四边形ADCE的形状是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
【解答】解:如图,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠HAE=∠ABC+∠ACB=2∠ABC,
∵AE是∠HAC的平分线,
∴∠HAE=∠CAE=∠HAC,
∴∠HAE=∠ABC,
∴AE∥BC,
又∵AB∥DE,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵AB=AC,AD⊥BC,
∴BD=DC,
∴AE=CD,
又∵AE∥DC,
∴四边形ADCE是平行四边形,
又∵AD⊥CD,
∴四边形ADCE是矩形,
故选:B.
4.如图,在平行四边形ABCD中,M、N是BD上两点,BM=DN,连接AM、MC、CN、NA,添加一个条件,使四边形AMCN是矩形,这个条件是( )
A.OM=AC B.MB=MO C.BD⊥AC D.∠AMB=∠CND
【解答】证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD
∵对角线BD上的两点M、N满足BM=DN,
∴OB﹣BM=OD﹣DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵OM=AC,
∴MN=AC,
∴四边形AMCN是矩形.
故选:A.
5.在?ABCD中,AC,BD交于点O,设∠DBC=α°,∠BOC=β°,若β关于α的函数解析式是β=180﹣2α(0<α<90),则下列说法正确的是( )
A.BO=BC B.OC=BC
C.四边形ABCD是菱形 D.四边形ABCD是矩形
【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵∠DBC=α°,∠BOC=β°,β=180﹣2α,
∴2α°+β°=180°,
∵∠DBC+∠BOC+∠OCB=180°,
即α°+β°+∠OCB=180°,
∴∠OCB=α°,
∴∠DBC=∠OCB,
∴OB=OC,
∴AC=BD,
∴?ABCD是矩形,
故选:D.
6.如图,直线EF∥MN,PQ交EF,MN于A,C两点,AB,CB,CD,AD分别是∠EAC,∠MCA,∠ACN,∠CAF的角平分线,则四边形ABCD是( )
A.菱形 B.平行四边形 C.矩形 D.不能确定
【解答】解:∵EF∥MN,
∴∠EAC+∠MCA=180°,
∵AB,CB,CD,AD分别是∠EAC,∠MCA,∠ACN,∠CAF的角平分线,∠EAF=180°,
∴∠BAC+∠BCA=90°,∠BAD=90°,
∴∠B=90°,
同理可得,∠D=90°,∠BCD=90°,
∴四边形ABCD是矩形,
故选:C.
7.如图,在锐角△ABC中,延长BC到点D,点O是AC边上的一个动点,过点O作直线MN∥BC,MN分别交∠ACB、∠ACD的平分线于E,F两点,连接AE、AF,在下列结论中:①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
【解答】解:∵MN∥CB,
∴∠OEC=∠BCE,∠OFC=∠ACF
∵∠ACE=∠BCE,∠ACF=∠DCF,
∴∠OEC=∠OCE,∠OFC=∠OCF,
∴OC=OE=OF,故①正确,
∵∠BCD=180°,
∴∠ECF=90°,
若EC=CF,则∠OFC=45°,显然不可能,故②错误,
∵∠ECF=90°,EC=12,CF=5,
∴EF==13,
∴OC=EF=6.5,故③错误,
∴OE=OF,OA=OC,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴四边形AECF是矩形.
故选:C.
二.填空题(共3小题)
8.如图,点E,F,G,H分别是BD,BC,AC,AD的中点:下列结论:①EH=EF;②当AB=CD,EG平分∠HGF;③当AB⊥CD时,四边形EFGH是矩形;其中正确的结论序号是 ②③ .
【解答】解:∵点E,F,G,H分别是BD,BC,AC,AD的中点,
∴EF∥CD,HG∥CD,EF=CD,HG=CD,HE=AB,AB∥HE,
∴EF=HG,EF∥HG,
∴四边形EFGH是平行四边形,
∵AB不一定等于CD,
∴EH不一定等于EF,故①错误,
∵AB=CD,
∴EH=EF,
∴平行四边形HEFG是菱形,
∴EG平分∠HGF,故②正确,
③∵AB⊥CD,
∴∠ABC+∠BCD=90°,
∵四边形HEFG是平行四边形,
∴GF∥HE∥AB,
∴∠GFC=∠ABC,
∵EF∥CD,
∴∠BFE=∠BCD,
∴∠GFC+∠EFB=90°,
∴∠EFG=90°,
∴平行四边形HEFG是矩形,故③正确,
故答案为:②③.
9.如图,将平行四边形ABCD的边DC延长到E,使CE=CD,连接AE交BC于F,∠AFC=n∠D,当n= 2 时,四边形ABEC是矩形.
【解答】解:当∠AFC=2∠D时,四边形ABEC是矩形.
∵四边形ABCD是平行四边形,
∴BC∥AD,∠BCE=∠D,
由题意易得AB∥EC,AB=EC,
∴四边形ABEC是平行四边形.
∵∠AFC=∠FEC+∠BCE,
∴当∠AFC=2∠D时,则有∠FEC=∠FCE,
∴FC=FE,
∴四边形ABEC是矩形,
故答案为:2.
10.如图,在平行四边形中,∠B=60°,AB=4,AD=6,动点F从D出发,以1个单位每秒的速度从D向A运动,同时动点E以相同速度从点C出发,沿BC方向在BC的延长线上运动,设运动时间为t,连接DE、CF.
探究:①当t= 4 s,四边形DECF是菱形;
②当t= 2 s,四边形DECF是矩形.
【解答】解:∵四边形ABCD为平行四边形,
∴AD∥BC,∠ADC=∠B=60°,CD=AB=4,
∴DF∥CE.
∵运动时间为t秒时,DF=t,CE=t,
∴DF=CE,
∴四边形DECF为平行四边形.
①当DF=CF时,可得出平行四边形DECF为菱形,
∵∠ADC=60°,DF=CF,
∴△CDF为等边三角形,
∴DF=CD=4,
∴t=4;
②当∠CFD=90°时,可得出平行四边形DECF为矩形,
∵∠ADC=60°,
∴∠DCF=30°,
∴DF=CD=2,
∴t=2.
故答案为:①4;②2.
三.解答题(共10小题)
11.如图,点C是BE的中点,四边形ABCD是平行四边形.
(1)求证:四边形ACED是平行四边形;
(2)如果AB=AE,求证:四边形ACED是矩形.
【解答】解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC.
∵点C是BE的中点,
∴BC=CE,
∴AD=CE,
∵AD∥CE,
∴四边形ACED是平行四边形;
(2)证明:∵四边形ABCD是平行四边形,
∴AB=DC,
∵AB=AE,
∴DC=AE,
∵四边形ACED是平行四边形,
∴四边形ACED是矩形.
12.如图,在平行四边形ABCD中,对角线AC、BD交于点O.
(1)若DE⊥AC于点E,BF⊥AC于点F,求证:AE=CF;
(2)若DO=AC,求证:四边形ABCD为矩形.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,
∴∠DAE=∠BCF,
∵DE⊥AC,BF⊥AC,
∴∠DEA=∠BFC=90°,
在△DEA与△BFC中,
,
∴△DEA≌△BFC(AAS),
∴AE=CF;
(2)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=BD,
∴OA=OC=OB=OD,
∴AC=BD,
∴平行四边形ABCD是矩形.
13.如图,在△ABC中,∠ACB=90°,D点是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.
(1)求∠CFD的度数;
(2)求证:四边形FDEC是矩形.
【解答】解:(1)∵∠ACB=90°,D是AB的中点,
∴AD=CD,
∵DF是∠ADC的角平分线,
∴DF⊥AC.
∴∠CFD=90°;
(2)证明:如图,
∵∠ACB=90°,D是AB的中点,
∴AD=CD,
∵DE是∠BDC的角平分线,
∴DE⊥AC.
∴∠DEC=90°,
∵∠CFD=90°,
∵∠ACB=90°,
∴四边形DECF是矩形.
14.如图,在等边△ABC中,点D是AC的中点,点F是BC的中点,以BD为边作等边△BDE,连接点A、E.求证:四边形AEBF为矩形.
【解答】证明:连接EF,
∵等边△ABC中,点D是AC的中点,F是BC的中点,
∴AF=BD,∠CBD=30°,
∵△BDE是等边三角形,
∴BE=BD,∠DBE=60°,
∴AF=BD=BE,∠EBF=∠AFB=90°,
在△ABF和△EFB中,
,
∴△ABF≌△EFB(SAS),
∴AB=EF,
∵∠AFB=∠EBF=90°,
∴AF∥BE,
又∵AF=BE,
∴四边形AEBF是平行四边形,
∵AB=EF,
∴四边形AEBF是矩形,
15.如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.
(1)求证:△AFE≌△DFB;
(2)求证:四边形ADCE是平行四边形;
(3)当AB、AC之间满足什么条件时,四边形ADCE是矩形.
【解答】证明:(1)∵AE∥BC,
∴∠AEF=∠DBF,且∠AFE=∠DFB,AF=DF
∴△AFE≌△DFB(AAS)
(2)∵△AFE≌△DFB,
∴AE=BD,
∵AD是△ABC的中线,
∴BD=CD
∴AE=CD
∵AE∥BC
∴四边形ADCE是平行四边形;
(3)当AB=AC时,四边形ADCE是矩形;
∵AB=AC,AD是△ABC的中线,
∴AD⊥BC,
∴∠ADC=90°
∵四边形ADCE是平行四边形
∴四边形ADCE是矩形
∴当AB=AC时,四边形ADCE是矩形.
16.如图,在?ABCD中,点E是AD的中点,连接BE,BE、CD的延长线相交于点F,连接AF、BD.
(1)求证:四边形ABDF是平行四边形;
(2)当∠C与∠BED满足条件 ∠BED=2∠C 时,四边形ABDF是矩形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴BA∥CD,
∴∠BAE=∠FDE,
∵点E是AD的中点,
∴AE=DE,
在△BEA和△FED中,
,
∴△BEA≌△FED(ASA),
∴AB=DF,
又∵AB∥DF,
∴四边形ABDF是平行四边形;
(2)∠BED=2∠C时,四边形ABDF是矩形,
证明:∵四边形ABCD是平行四边形,
∴∠BAE=∠C,
∵∠BED=2∠C,
∴∠BED=2∠BAE,
∵∠BED=∠BAE+∠ABE,
∴∠BAE=∠ABE,
∴EB=EA,
由(1)知四边形ABDF是平行四边形,
∴BE=EF,
∴EA=EF,
∴∠EAF=∠EFA,
∵∠BAE+∠ABE+∠EAF+∠EFA=180°,
∴∠BAE+∠EAF=90°,
∴四边形ABDF是矩形.
17.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当线段AB与线段AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,OA=OC,
∴∠ABE=∠CDF,
∵点E,F分别为OB,OD的中点,
∴BE=OB,DF=OD,
∴BE=DF,
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS);
(2)解:当AC=2AB时,四边形EGCF是矩形;理由如下:
∵AC=2OA,AC=2AB,
∴AB=OA,
∵E是OB的中点,
∴AG⊥OB,
∴∠OEG=90°,
同理:CF⊥OD,
∴AG∥CF,
∴EG∥CF,
∵EG=AE,OA=OC,
∴OE是△ACG的中位线,
∴OE∥CG,
∴EF∥CG,
∴四边形EGCF是平行四边形,
∵∠OEG=90°,
∴四边形EGCF是矩形.
18.如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;
【解答】解:(1)OE=OF,理由如下:
∵MN∥BC,
∴∠OEC=∠ECB,
∵CE平分∠ACB,
∴∠ACE=∠ECB,
∴∠OEC=∠ACE,
∴OE=OC,
同理可得:OC=OF,
∴OE=OF;
(2)当O为AC中点时,四边形AECF是矩形;
理由如下:
∵OA=OC,OE=OF(已证),
∴四边形AECF是平行四边形,
∵EC平分∠ACB,CF平分∠ACG,
∴∠ACE=∠ACB,∠ACF=∠ACG,
∴∠ACE+∠ACF=(∠ACB+∠ACG)=×180°=90°,
即∠ECF=90°,
∴四边形AECF是矩形.
19.如图,△ABC的中线AD、BE、CF相交于点G,H、I分别是BG、CG的中点.
(1) EF 是△ABC的中位线,EF与BC位置关系是 EF∥BC 、数量关系是 EF=BC ; HI 是△GBC的中位线,HI与BC位置关系是 HI∥BC 、数量关系是 HI=BC ;
(2)求证:四边形EFHI是平行四边形;
(3)当AD与BC满足条件 AD⊥BC 时,四边形EFHI是矩形.(直接写出结论)当AD与BC满足条件 BC=AD 时,四边形EFHI是菱形.(直接写出结论)
【解答】(1)解:∵BE、CF是△ABC的中线,
∴AE=CE,AF=BF,
∴EF是△ABC的中位线,
∴EF∥BC,EF=BC,
∵H、I分别是BG、CG的中点,
∴HI是△GBC的中位线,
∴HI∥BC,HI=BC,
故答案为:EF,EF∥BC、EF=BC;HI,HI∥BC、HI=BC;
(2)证明:由(1)得:EF∥BC,EF=BC,HI∥BC,HI=BC,
∴EF∥HI,EF=HI,
∴四边形EFHI是平行四边形;
(3)当AD与BC满足条件AD⊥BC时,四边形EFHI是矩形;理由如下:
同(1)得:FH是△ABG的中位线,
∴FH∥AG,FH=AG,
∴FH∥AD,
∵EF∥BC,AD⊥BC,
∴EF⊥FH,
∴∠EFH=90°,
∵四边形EFHI是平行四边形,
∴四边形EFHI是矩形;
当AD与BC满足条件BC=AD时,四边形EFHI是菱形;理由如下:
∵△ABC的中线AD、BE、CF相交于点G,
∴AG=AD,
∵BC=AD,
∴AG=BC,
∵FH=AG,EF=BC,
∴FH=EF,
又∵四边形EFHI是平行四边形,
∴四边形EFHI是菱形;
故答案为:AD⊥BC,BC=AD.
20.已知:如图,AC、BD相交于点O,且点O是AC、BD的中点,点E在四边形ABCD的形外,且∠AEC=∠BED=90°.求证:四边形ABCD是矩形.
【解答】证明:连接EO,如图所示:
∵O是AC、BD的中点,
∴AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
在Rt△EBD中,
∵O为BD中点,
∴EO=BD,
在Rt△AEC中,∵O为AC的中点,
∴EO=AC,
∴AC=BD,
又∵四边形ABCD是平行四边形,
∴平行四边形ABCD是矩形.
一.选择题(共7小题)
1.如图,D、E、F分别是△ABC各边中点,则以下说法错误的是( )
397764068580A.△BDE和△DCF的面积相等
B.四边形AEDF是平行四边形
C.若AB=BC,则四边形AEDF是菱形
D.若∠A=90°,则四边形AEDF是矩形
2.下列说法正确的是( )
A.有一组对角是直角的四边形一定是矩形
B.一条对角线被另一条对角线垂直平分的四边形是菱形
C.对角互补的平行四边形是矩形
D.对角线相等的四边形是矩形
3.如图,在△ABC中,AB=AC,AD⊥BC于点D,AE是∠BAC的外角的平分线,DE∥AB交AE于点E,则四边形ADCE的形状是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
4.如图,在平行四边形ABCD中,M、N是BD上两点,BM=DN,连接AM、MC、CN、NA,添加一个条件,使四边形AMCN是矩形,这个条件是( )
A.OM=AC B.MB=MO C.BD⊥AC D.∠AMB=∠CND
31623007620099060076200
第3题 第4题
5.在?ABCD中,AC,BD交于点O,设∠DBC=α°,∠BOC=β°,若β关于α的函数解析式是β=180﹣2α(0<α<90),则下列说法正确的是( )
A.BO=BC B.OC=BC
C.四边形ABCD是菱形 D.四边形ABCD是矩形
6.如图,直线EF∥MN,PQ交EF,MN于A,C两点,AB,CB,CD,AD分别是∠EAC,∠MCA,∠ACN,∠CAF的角平分线,则四边形ABCD是( )
A.菱形 B.平行四边形 C.矩形 D.不能确定
7.如图,在锐角△ABC中,延长BC到点D,点O是AC边上的一个动点,过点O作直线MN∥BC,MN分别交∠ACB、∠ACD的平分线于E,F两点,连接AE、AF,在下列结论中:①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
86868076200359664076200
第6题 第7题
二.填空题(共3小题)
8.如图,点E,F,G,H分别是BD,BC,AC,AD的中点:下列结论:①EH=EF;②当AB=CD,EG平分∠HGF;③当AB⊥CD时,四边形EFGH是矩形;其中正确的结论序号是 .
9.如图,将平行四边形ABCD的边DC延长到E,使CE=CD,连接AE交BC于F,∠AFC=n∠D,当n= 时,四边形ABEC是矩形.
10.如图,在平行四边形中,∠B=60°,AB=4,AD=6,动点F从D出发,以1个单位每秒的速度从D向A运动,同时动点E以相同速度从点C出发,沿BC方向在BC的延长线上运动,设运动时间为t,连接DE、CF.
探究:①当t= s,四边形DECF是菱形;
②当t= s,四边形DECF是矩形.
23317207620023622076200455676076200
第8题 第9题 第10题
三.解答题(共10小题)
11.如图,点C是BE的中点,四边形ABCD是平行四边形.
(1)求证:四边形ACED是平行四边形;
(2)如果AB=AE,求证:四边形ACED是矩形.
12.如图,在平行四边形ABCD中,对角线AC、BD交于点O.
(1)若DE⊥AC于点E,BF⊥AC于点F,求证:AE=CF;
(2)若DO=AC,求证:四边形ABCD为矩形.
13.如图,在△ABC中,∠ACB=90°,D点是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.
(1)求∠CFD的度数;
(2)求证:四边形FDEC是矩形.
14.如图,在等边△ABC中,点D是AC的中点,点F是BC的中点,以BD为边作等边△BDE,连接点A、E.求证:四边形AEBF为矩形.
15.如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.
(1)求证:△AFE≌△DFB;
(2)求证:四边形ADCE是平行四边形;
(3)当AB、AC之间满足什么条件时,四边形ADCE是矩形.
16.如图,在?ABCD中,点E是AD的中点,连接BE,BE、CD的延长线相交于点F,连接AF、BD.
(1)求证:四边形ABDF是平行四边形;
(2)当∠C与∠BED满足条件 时,四边形ABDF是矩形.
17.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当线段AB与线段AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
18.如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;
19.如图,△ABC的中线AD、BE、CF相交于点G,H、I分别是BG、CG的中点.
(1) 是△ABC的中位线,EF与BC位置关系是 、数量关系是 ; 是△GBC的中位线,HI与BC位置关系是 、数量关系是 ;
(2)求证:四边形EFHI是平行四边形;
(3)当AD与BC满足条件 时,四边形EFHI是矩形.(直接写出结论)当AD与BC满足条件 时,四边形EFHI是菱形.(直接写出结论)
20.已知:如图,AC、BD相交于点O,且点O是AC、BD的中点,点E在四边形ABCD的形外,且∠AEC=∠BED=90°.求证:四边形ABCD是矩形.
1.2.1矩形的判定同步练习
参考答案与试题解析
一.选择题(共7小题)
1.如图,D、E、F分别是△ABC各边中点,则以下说法错误的是( )
A.△BDE和△DCF的面积相等
B.四边形AEDF是平行四边形
C.若AB=BC,则四边形AEDF是菱形
D.若∠A=90°,则四边形AEDF是矩形
【解答】解:A.连接EF,
∵D、E、F分别是△ABC各边中点,
∴EF∥BC,BD=CD,
设EF和BC间的距离为h,
∴S△BDE=BD?h,S△DCE=CD?h,
∴S△BDE=S△DCE,
故本选项不符合题意;
B.∵D、E、F分别是△ABC各边中点,
∴DE∥AC,DF∥AB,
∴DE∥AF,DF∥AE,
∴四边形AEDF是平行四边形,
故本选项不符合题意;
C.∵D、E、F分别是△ABC各边中点,
∴EF=BC,DF=AB,
若AB=BC,则FE=DF,
∴四边形AEDF不一定是菱形,
故本选项符合题意;
D.∵四边形AEDF是平行四边形,
∴若∠A=90°,则四边形AEDF是矩形,
故本选项不符合题意;
故选:C.
2.下列说法正确的是( )
A.有一组对角是直角的四边形一定是矩形
B.一条对角线被另一条对角线垂直平分的四边形是菱形
C.对角互补的平行四边形是矩形
D.对角线相等的四边形是矩形
【解答】解:∵有一组对角是直角的四边形不一定是矩形,
∴选项A不正确;
∵两条对角线互相垂直平分的四边形是菱形,
∴选项B不正确;
∵对角互补的平行四边形一定是矩形,
∴选项C正确;
∵对角线相等的平行四边形是矩形,
∴选项D错误;
故选:C.
3.如图,在△ABC中,AB=AC,AD⊥BC于点D,AE是∠BAC的外角的平分线,DE∥AB交AE于点E,则四边形ADCE的形状是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
【解答】解:如图,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠HAE=∠ABC+∠ACB=2∠ABC,
∵AE是∠HAC的平分线,
∴∠HAE=∠CAE=∠HAC,
∴∠HAE=∠ABC,
∴AE∥BC,
又∵AB∥DE,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵AB=AC,AD⊥BC,
∴BD=DC,
∴AE=CD,
又∵AE∥DC,
∴四边形ADCE是平行四边形,
又∵AD⊥CD,
∴四边形ADCE是矩形,
故选:B.
4.如图,在平行四边形ABCD中,M、N是BD上两点,BM=DN,连接AM、MC、CN、NA,添加一个条件,使四边形AMCN是矩形,这个条件是( )
A.OM=AC B.MB=MO C.BD⊥AC D.∠AMB=∠CND
【解答】证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD
∵对角线BD上的两点M、N满足BM=DN,
∴OB﹣BM=OD﹣DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵OM=AC,
∴MN=AC,
∴四边形AMCN是矩形.
故选:A.
5.在?ABCD中,AC,BD交于点O,设∠DBC=α°,∠BOC=β°,若β关于α的函数解析式是β=180﹣2α(0<α<90),则下列说法正确的是( )
A.BO=BC B.OC=BC
C.四边形ABCD是菱形 D.四边形ABCD是矩形
【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵∠DBC=α°,∠BOC=β°,β=180﹣2α,
∴2α°+β°=180°,
∵∠DBC+∠BOC+∠OCB=180°,
即α°+β°+∠OCB=180°,
∴∠OCB=α°,
∴∠DBC=∠OCB,
∴OB=OC,
∴AC=BD,
∴?ABCD是矩形,
故选:D.
6.如图,直线EF∥MN,PQ交EF,MN于A,C两点,AB,CB,CD,AD分别是∠EAC,∠MCA,∠ACN,∠CAF的角平分线,则四边形ABCD是( )
A.菱形 B.平行四边形 C.矩形 D.不能确定
【解答】解:∵EF∥MN,
∴∠EAC+∠MCA=180°,
∵AB,CB,CD,AD分别是∠EAC,∠MCA,∠ACN,∠CAF的角平分线,∠EAF=180°,
∴∠BAC+∠BCA=90°,∠BAD=90°,
∴∠B=90°,
同理可得,∠D=90°,∠BCD=90°,
∴四边形ABCD是矩形,
故选:C.
7.如图,在锐角△ABC中,延长BC到点D,点O是AC边上的一个动点,过点O作直线MN∥BC,MN分别交∠ACB、∠ACD的平分线于E,F两点,连接AE、AF,在下列结论中:①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
【解答】解:∵MN∥CB,
∴∠OEC=∠BCE,∠OFC=∠ACF
∵∠ACE=∠BCE,∠ACF=∠DCF,
∴∠OEC=∠OCE,∠OFC=∠OCF,
∴OC=OE=OF,故①正确,
∵∠BCD=180°,
∴∠ECF=90°,
若EC=CF,则∠OFC=45°,显然不可能,故②错误,
∵∠ECF=90°,EC=12,CF=5,
∴EF==13,
∴OC=EF=6.5,故③错误,
∴OE=OF,OA=OC,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴四边形AECF是矩形.
故选:C.
二.填空题(共3小题)
8.如图,点E,F,G,H分别是BD,BC,AC,AD的中点:下列结论:①EH=EF;②当AB=CD,EG平分∠HGF;③当AB⊥CD时,四边形EFGH是矩形;其中正确的结论序号是 ②③ .
【解答】解:∵点E,F,G,H分别是BD,BC,AC,AD的中点,
∴EF∥CD,HG∥CD,EF=CD,HG=CD,HE=AB,AB∥HE,
∴EF=HG,EF∥HG,
∴四边形EFGH是平行四边形,
∵AB不一定等于CD,
∴EH不一定等于EF,故①错误,
∵AB=CD,
∴EH=EF,
∴平行四边形HEFG是菱形,
∴EG平分∠HGF,故②正确,
③∵AB⊥CD,
∴∠ABC+∠BCD=90°,
∵四边形HEFG是平行四边形,
∴GF∥HE∥AB,
∴∠GFC=∠ABC,
∵EF∥CD,
∴∠BFE=∠BCD,
∴∠GFC+∠EFB=90°,
∴∠EFG=90°,
∴平行四边形HEFG是矩形,故③正确,
故答案为:②③.
9.如图,将平行四边形ABCD的边DC延长到E,使CE=CD,连接AE交BC于F,∠AFC=n∠D,当n= 2 时,四边形ABEC是矩形.
【解答】解:当∠AFC=2∠D时,四边形ABEC是矩形.
∵四边形ABCD是平行四边形,
∴BC∥AD,∠BCE=∠D,
由题意易得AB∥EC,AB=EC,
∴四边形ABEC是平行四边形.
∵∠AFC=∠FEC+∠BCE,
∴当∠AFC=2∠D时,则有∠FEC=∠FCE,
∴FC=FE,
∴四边形ABEC是矩形,
故答案为:2.
10.如图,在平行四边形中,∠B=60°,AB=4,AD=6,动点F从D出发,以1个单位每秒的速度从D向A运动,同时动点E以相同速度从点C出发,沿BC方向在BC的延长线上运动,设运动时间为t,连接DE、CF.
探究:①当t= 4 s,四边形DECF是菱形;
②当t= 2 s,四边形DECF是矩形.
【解答】解:∵四边形ABCD为平行四边形,
∴AD∥BC,∠ADC=∠B=60°,CD=AB=4,
∴DF∥CE.
∵运动时间为t秒时,DF=t,CE=t,
∴DF=CE,
∴四边形DECF为平行四边形.
①当DF=CF时,可得出平行四边形DECF为菱形,
∵∠ADC=60°,DF=CF,
∴△CDF为等边三角形,
∴DF=CD=4,
∴t=4;
②当∠CFD=90°时,可得出平行四边形DECF为矩形,
∵∠ADC=60°,
∴∠DCF=30°,
∴DF=CD=2,
∴t=2.
故答案为:①4;②2.
三.解答题(共10小题)
11.如图,点C是BE的中点,四边形ABCD是平行四边形.
(1)求证:四边形ACED是平行四边形;
(2)如果AB=AE,求证:四边形ACED是矩形.
【解答】解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC.
∵点C是BE的中点,
∴BC=CE,
∴AD=CE,
∵AD∥CE,
∴四边形ACED是平行四边形;
(2)证明:∵四边形ABCD是平行四边形,
∴AB=DC,
∵AB=AE,
∴DC=AE,
∵四边形ACED是平行四边形,
∴四边形ACED是矩形.
12.如图,在平行四边形ABCD中,对角线AC、BD交于点O.
(1)若DE⊥AC于点E,BF⊥AC于点F,求证:AE=CF;
(2)若DO=AC,求证:四边形ABCD为矩形.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,
∴∠DAE=∠BCF,
∵DE⊥AC,BF⊥AC,
∴∠DEA=∠BFC=90°,
在△DEA与△BFC中,
,
∴△DEA≌△BFC(AAS),
∴AE=CF;
(2)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=BD,
∴OA=OC=OB=OD,
∴AC=BD,
∴平行四边形ABCD是矩形.
13.如图,在△ABC中,∠ACB=90°,D点是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.
(1)求∠CFD的度数;
(2)求证:四边形FDEC是矩形.
【解答】解:(1)∵∠ACB=90°,D是AB的中点,
∴AD=CD,
∵DF是∠ADC的角平分线,
∴DF⊥AC.
∴∠CFD=90°;
(2)证明:如图,
∵∠ACB=90°,D是AB的中点,
∴AD=CD,
∵DE是∠BDC的角平分线,
∴DE⊥AC.
∴∠DEC=90°,
∵∠CFD=90°,
∵∠ACB=90°,
∴四边形DECF是矩形.
14.如图,在等边△ABC中,点D是AC的中点,点F是BC的中点,以BD为边作等边△BDE,连接点A、E.求证:四边形AEBF为矩形.
【解答】证明:连接EF,
∵等边△ABC中,点D是AC的中点,F是BC的中点,
∴AF=BD,∠CBD=30°,
∵△BDE是等边三角形,
∴BE=BD,∠DBE=60°,
∴AF=BD=BE,∠EBF=∠AFB=90°,
在△ABF和△EFB中,
,
∴△ABF≌△EFB(SAS),
∴AB=EF,
∵∠AFB=∠EBF=90°,
∴AF∥BE,
又∵AF=BE,
∴四边形AEBF是平行四边形,
∵AB=EF,
∴四边形AEBF是矩形,
15.如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.
(1)求证:△AFE≌△DFB;
(2)求证:四边形ADCE是平行四边形;
(3)当AB、AC之间满足什么条件时,四边形ADCE是矩形.
【解答】证明:(1)∵AE∥BC,
∴∠AEF=∠DBF,且∠AFE=∠DFB,AF=DF
∴△AFE≌△DFB(AAS)
(2)∵△AFE≌△DFB,
∴AE=BD,
∵AD是△ABC的中线,
∴BD=CD
∴AE=CD
∵AE∥BC
∴四边形ADCE是平行四边形;
(3)当AB=AC时,四边形ADCE是矩形;
∵AB=AC,AD是△ABC的中线,
∴AD⊥BC,
∴∠ADC=90°
∵四边形ADCE是平行四边形
∴四边形ADCE是矩形
∴当AB=AC时,四边形ADCE是矩形.
16.如图,在?ABCD中,点E是AD的中点,连接BE,BE、CD的延长线相交于点F,连接AF、BD.
(1)求证:四边形ABDF是平行四边形;
(2)当∠C与∠BED满足条件 ∠BED=2∠C 时,四边形ABDF是矩形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴BA∥CD,
∴∠BAE=∠FDE,
∵点E是AD的中点,
∴AE=DE,
在△BEA和△FED中,
,
∴△BEA≌△FED(ASA),
∴AB=DF,
又∵AB∥DF,
∴四边形ABDF是平行四边形;
(2)∠BED=2∠C时,四边形ABDF是矩形,
证明:∵四边形ABCD是平行四边形,
∴∠BAE=∠C,
∵∠BED=2∠C,
∴∠BED=2∠BAE,
∵∠BED=∠BAE+∠ABE,
∴∠BAE=∠ABE,
∴EB=EA,
由(1)知四边形ABDF是平行四边形,
∴BE=EF,
∴EA=EF,
∴∠EAF=∠EFA,
∵∠BAE+∠ABE+∠EAF+∠EFA=180°,
∴∠BAE+∠EAF=90°,
∴四边形ABDF是矩形.
17.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当线段AB与线段AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,OA=OC,
∴∠ABE=∠CDF,
∵点E,F分别为OB,OD的中点,
∴BE=OB,DF=OD,
∴BE=DF,
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS);
(2)解:当AC=2AB时,四边形EGCF是矩形;理由如下:
∵AC=2OA,AC=2AB,
∴AB=OA,
∵E是OB的中点,
∴AG⊥OB,
∴∠OEG=90°,
同理:CF⊥OD,
∴AG∥CF,
∴EG∥CF,
∵EG=AE,OA=OC,
∴OE是△ACG的中位线,
∴OE∥CG,
∴EF∥CG,
∴四边形EGCF是平行四边形,
∵∠OEG=90°,
∴四边形EGCF是矩形.
18.如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;
【解答】解:(1)OE=OF,理由如下:
∵MN∥BC,
∴∠OEC=∠ECB,
∵CE平分∠ACB,
∴∠ACE=∠ECB,
∴∠OEC=∠ACE,
∴OE=OC,
同理可得:OC=OF,
∴OE=OF;
(2)当O为AC中点时,四边形AECF是矩形;
理由如下:
∵OA=OC,OE=OF(已证),
∴四边形AECF是平行四边形,
∵EC平分∠ACB,CF平分∠ACG,
∴∠ACE=∠ACB,∠ACF=∠ACG,
∴∠ACE+∠ACF=(∠ACB+∠ACG)=×180°=90°,
即∠ECF=90°,
∴四边形AECF是矩形.
19.如图,△ABC的中线AD、BE、CF相交于点G,H、I分别是BG、CG的中点.
(1) EF 是△ABC的中位线,EF与BC位置关系是 EF∥BC 、数量关系是 EF=BC ; HI 是△GBC的中位线,HI与BC位置关系是 HI∥BC 、数量关系是 HI=BC ;
(2)求证:四边形EFHI是平行四边形;
(3)当AD与BC满足条件 AD⊥BC 时,四边形EFHI是矩形.(直接写出结论)当AD与BC满足条件 BC=AD 时,四边形EFHI是菱形.(直接写出结论)
【解答】(1)解:∵BE、CF是△ABC的中线,
∴AE=CE,AF=BF,
∴EF是△ABC的中位线,
∴EF∥BC,EF=BC,
∵H、I分别是BG、CG的中点,
∴HI是△GBC的中位线,
∴HI∥BC,HI=BC,
故答案为:EF,EF∥BC、EF=BC;HI,HI∥BC、HI=BC;
(2)证明:由(1)得:EF∥BC,EF=BC,HI∥BC,HI=BC,
∴EF∥HI,EF=HI,
∴四边形EFHI是平行四边形;
(3)当AD与BC满足条件AD⊥BC时,四边形EFHI是矩形;理由如下:
同(1)得:FH是△ABG的中位线,
∴FH∥AG,FH=AG,
∴FH∥AD,
∵EF∥BC,AD⊥BC,
∴EF⊥FH,
∴∠EFH=90°,
∵四边形EFHI是平行四边形,
∴四边形EFHI是矩形;
当AD与BC满足条件BC=AD时,四边形EFHI是菱形;理由如下:
∵△ABC的中线AD、BE、CF相交于点G,
∴AG=AD,
∵BC=AD,
∴AG=BC,
∵FH=AG,EF=BC,
∴FH=EF,
又∵四边形EFHI是平行四边形,
∴四边形EFHI是菱形;
故答案为:AD⊥BC,BC=AD.
20.已知:如图,AC、BD相交于点O,且点O是AC、BD的中点,点E在四边形ABCD的形外,且∠AEC=∠BED=90°.求证:四边形ABCD是矩形.
【解答】证明:连接EO,如图所示:
∵O是AC、BD的中点,
∴AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
在Rt△EBD中,
∵O为BD中点,
∴EO=BD,
在Rt△AEC中,∵O为AC的中点,
∴EO=AC,
∴AC=BD,
又∵四边形ABCD是平行四边形,
∴平行四边形ABCD是矩形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
