人教新课标版七下实际问题与二元一次方程(第2课标)一案三单设计
文档属性
| 名称 | 人教新课标版七下实际问题与二元一次方程(第2课标)一案三单设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 98.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-18 00:00:00 | ||
图片预览



文档简介
【教材地位分析】
本节内容是在学生掌握了二元一次方程组的解法,能列二元一次方程组解较简单的应用题的基础上安排的,其中的“牛饲料问题”“种植计划问题”“成本与产出问题”是具有一定综合性的问题,涉及到估算与精确计算的比较、开放地探索设计方案、根据图表信息列方程组等问题形式.
分析数量关系列出方程组是学习的难点,能正确规范的解决各种各样的实际问题是学习的重点,其中列出方程组如何解是容易忽视的环节,要加强运算速度、准确度的训练,努力做到会的题目保证做对.
【重点、难点】
教学重点:正确理解题目中关键语句的含义,找出等量关系,列二元一次方程组
教学难点:设辅助未知量,用式子正确表示题目中的等量关系
【教学目标】
知识与技能目标:
1、会根据具体问题中的数量关系,经过自主探索、互相交流,列出二元一次方程组并求解,养成对所得结果进行检验的意识;
2、能熟练地列二元一次方程组解决简单的实际问题;
3、通过将实际问题中的数量关系转化为二元一次方程组,体会数学化的过程,提高用数学分析和解决问题的能力。
过程与方法目标:
经历探索、研究、交流的过程,将实际情景中的数量关系抽象出来。
情感与态度目标:
通过实际问题,感受二元一次方程组的广泛应用,加深对数学模型的认识,增强数学的应用意识。
【学生分析】
由于本节需要探究的问题比较复杂,所以学生感到学习难度较大,所以引导学生分析问题就成了重中之重,限于学生的年龄特点和知识积累的量太少,应循序渐进,由易到难,由简单到复杂,避免是学生产生厌学心理。
【设计理念】
1.尊重学生的心里发展的特点,利用情境教学,来调动学生的学习积极性。
2.加强同学之间的合作,通过学生的交流、合作,培养学生的团结意识。
【教学方法】
引导学生课前用好《问题导读---评价单》,对所学知识进行提前预习,找出难理解的问题,以便上课更有针对性。
通过创设情境,将复杂的问题适当分解,用问题引导学生积极思考、努力探索.教学过程实际上就是系列问题探究、解决的过程,学生在教师指导下以问题解决为中心,通过自主探索、合作交流完成各项教学任务,在探索中获得新知,发展能力.引导学生充分利用《问题生成---评价单》。
然后辅之《问题训练---评价单》进行课堂知识的巩固和验证。
【教师课前准备】
《问题导读---评价单》、《问题生成---评价单》、《问题训练---评价单》
【教学过程设计】
问题与情境 师生行为 设计意图
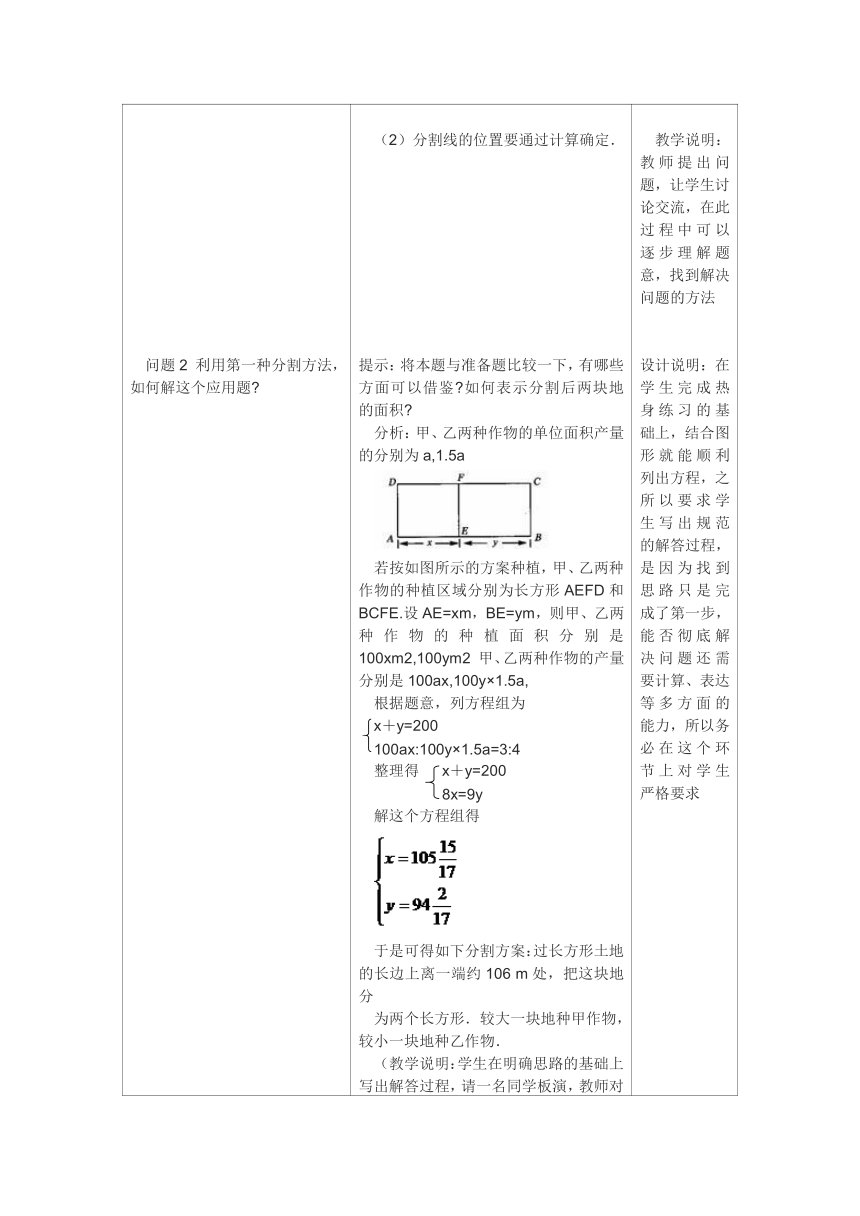
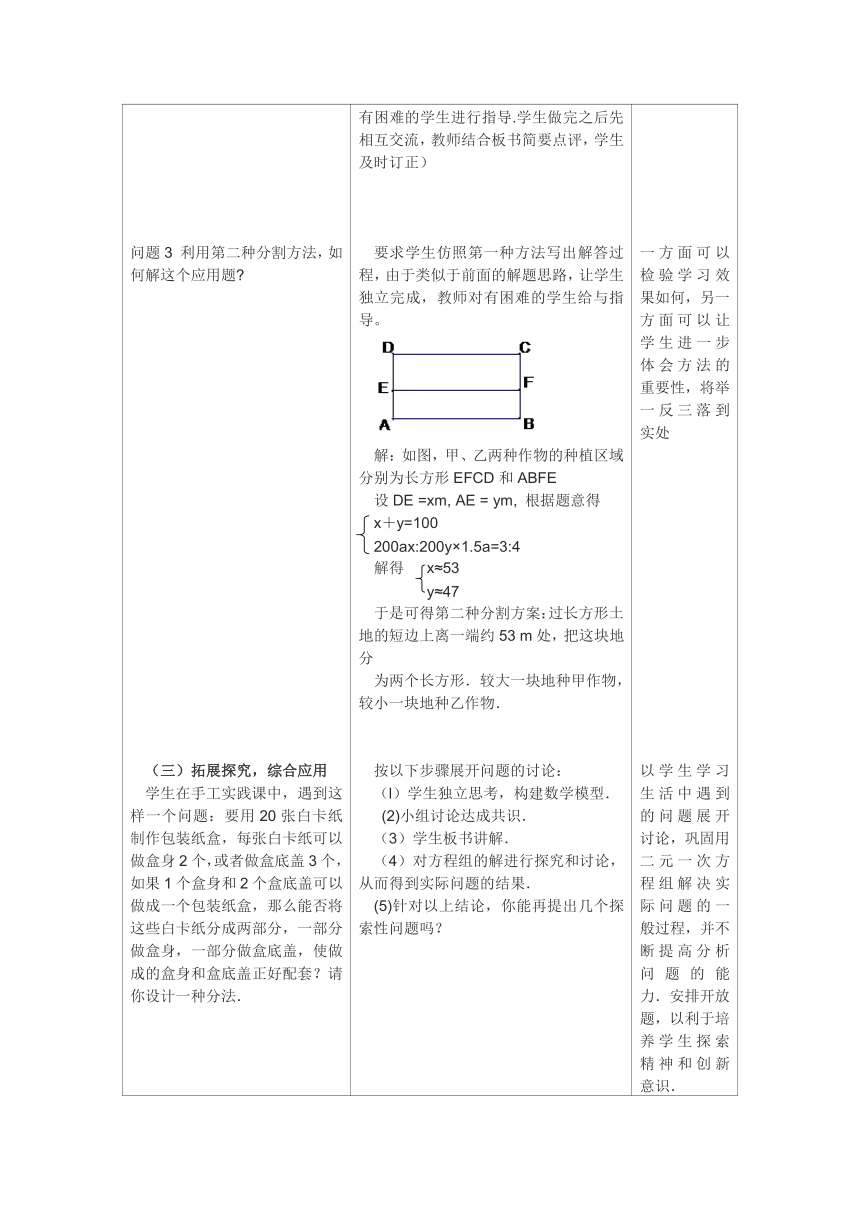
(一)创设情境前面我们初步体验了用方程组解决实际问题的全过程,其实生产、生活中还有许多问题也能用方程组解决.甲、乙两种作物的单位面积产量的比是2:3,现有一块面积17公顷的土地,要在这块土地上种植这两种作物,且使甲、乙两种作物的总产量的比是3:4,甲、乙两种作物的种植面积分别是多少 (二)、探索新知,讲授新课教材106页探究2据统计资料,甲、乙两种作物的单位面积产量的比是1:1.5,现要在一块长200 m,宽100 m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是3:4(结果取整数) 问题1:动手画一画,可能有哪些划分方案 分割线的位置有哪些条件决定 问题2 利用第一种分割方法,如何解这个应用题 问题3 利用第二种分割方法,如何解这个应用题 (三)拓展探究,综合应用学生在手工实践课中,遇到这样一个问题:要用20张白卡纸制作包装纸盒,每张白卡纸可以做盒身2个,或者做盒底盖3个,如果1个盒身和2个盒底盖可以做成一个包装纸盒,那么能否将这些白卡纸分成两部分,一部分做盒身,一部分做盒底盖,使做成的盒身和盒底盖正好配套?请你设计一种分法.(四)、接受考验发放《问题训练---评价单》,学生独立完成上面的练习题(五)反思回顾问题1:本节课你学习了什么 问题2:本节课你有哪些收获 问题3:通过今天的学习,你想进一步探究的问题是什么 课前让学生利用《问题导读---评价单》进行预习,以便对本节课有一个更清晰的认识。解:设甲种作物的单位面积产量为2a,种植面积为x公顷,乙种作物的单位面积产量为3a,种植面积分别为y公顷,根据题意得x+y=172ax:3ay=3:4解得 x=9y=8答:甲、乙两种作物的种植面积分别是9公顷,8公顷教学说明:教师提出问题,学生尝试解答,两名学生板演,结合板演订正,提醒学生注意准确理解关键词语“甲、乙两种作物的单位面积产量的比是2:3”“甲、乙两种作物的总产量的比是3:4”的含义发放《问题生成---评价单》,然后分组讨论上面教师出示的问题,并进行归纳和整理,得出结论,然后请小组代表发言。然后学生整理方程写出规范的解题过程多角度分析问题,多策略解决问题,提高思维的发散性。学生通过动手操作、动脑思考、讨论交流,初步明确了以下问题(1)有两种方法分割长方形(2)分割线的位置要通过计算确定.提示:将本题与准备题比较一下,有哪些方面可以借鉴 如何表示分割后两块地的面积 分析:甲、乙两种作物的单位面积产量的分别为a,1.5a若按如图所示的方案种植,甲、乙两种作物的种植区域分别为长方形AEFD和BCFE.设AE=xm,BE=ym,则甲、乙两种作物的种植面积分别是100xm2,100ym2 甲、乙两种作物的产量分别是100ax,100y×1.5a,根据题意,列方程组为 x+y=200100ax:100y×1.5a=3:4整理得 x+y=2008x=9y解这个方程组得于是可得如下分割方案:过长方形土地的长边上离一端约106 m处,把这块地分为两个长方形.较大一块地种甲作物,较小一块地种乙作物.(教学说明:学生在明确思路的基础上写出解答过程,请一名同学板演,教师对有困难的学生进行指导.学生做完之后先相互交流,教师结合板书简要点评,学生及时订正)要求学生仿照第一种方法写出解答过程,由于类似于前面的解题思路,让学生独立完成,教师对有困难的学生给与指导。解:如图,甲、乙两种作物的种植区域分别为长方形EFCD和ABFE设DE =xm, AE = ym, 根据题意得x+y=100200ax:200y×1.5a=3:4解得 x≈53y≈47于是可得第二种分割方案:过长方形土地的短边上离一端约53 m处,把这块地分为两个长方形.较大一块地种甲作物,较小一块地种乙作物.按以下步骤展开问题的讨论:(l)学生独立思考,构建数学模型. (2)小组讨论达成共识.(3)学生板书讲解.(4)对方程组的解进行探究和讨论,从而得到实际问题的结果.(5)针对以上结论,你能再提出几个探索性问题吗?从不同角度设计练习,巩固学生所学,然后教师给予评价,把出现问题多的题目,给予重点讲解。学生口述本节课所学的内容。师生共同回顾小结。要求学生课后规范作业。 由于探究2种的问题学生较陌生,并且难度较大,所以先设计一个较简单的题目作铺垫,一方面让学生熟悉常用的数量关系,另一方面熟悉列方程解应用题的一般步骤,同时分散探究2的难点引导学生用画图的方式探寻解题思路,使学生先从总体上明确要做什么,然后考虑怎样做的问题教学说明:教师提出问题,让学生讨论交流,在此过程中可以逐步理解题意,找到解决问题的方法设计说明:在学生完成热身练习的基础上,结合图形就能顺利列出方程,之所以要求学生写出规范的解答过程,是因为找到思路只是完成了第一步,能否彻底解决问题还需要计算、表达等多方面的能力,所以务必在这个环节上对学生严格要求一方面可以检验学习效果如何,另一方面可以让学生进一步体会方法的重要性,将举一反三落到实处以学生学习生活中遇到的问题展开讨论,巩固用二元一次方程组解决实际问题的一般过程,并不断提高分析问题的能力.安排开放题,以利于培养学生探索精神和创新意识.通过练习题的练习可以规范解题步骤,培养学生有条理地思考、表达的习惯。以上设计再次通过对三个问题的思考引导学生回顾自己的学习过程,畅所欲言,加强反思、提炼及知识的归纳,纳入自己的知识结构
教学反思
1.本节主要学习用画图的方法分析数量关系,通过列二元一次方程组设计方案.2.主要用到的思想方法是方程思想:将实际问题转化成二元一次方程组解决3.注意的问题:(1)认真审题,准确理解关键语句的含义.(2)解出方程组时要选择适当的方法,提高运算速度、准确度..(3)从多角度寻求解决问题的途径.
《实际问题和二元一次方程(2)问题导读——评价单》
设计者: 班级: 姓名:
知识与技能目标:
1、会根据具体问题中的数量关系,经过自主探索、互相交流,列出二元一次方程组并求解,养成对所得结果进行检验的意识;
2、能熟练地列二元一次方程组解决简单的实际问题;
3、通过将实际问题中的数量关系转化为二元一次方程组,体会数学化的过程,提高用数学分析和解决问题的能力。
过程与方法目标:
经历探索、研究、交流的过程,将实际情景中的数量关系抽象出来。
情感与态度目标:
通过实际问题,感受二元一次方程组的广泛应用,加深对数学模型的认识,增强数学的应用意识。
为你导航
1.某市现有42万人口,计划一年后城镇人口增加0.8%,农村人口增加1.1%,这样全市人口将增加1%,求这个市现在的城镇人口与农村人口?
设城镇人口是x万,农村人口是y万,根据题意填写下表,并列出方程组求x、y的值。
城镇 农村 全市
现有人数(万人) x y 42
一年后增加人口(万人)
2.某汽车制造厂接受了在预定期限内生产一批汽车的任务,如果每天生产35辆,则差10辆才能完成任务;如果每天生产40辆,则可超额生产20辆。试求预定期限是多少天?计划生产多少辆汽车?
若设预定期限为x天,计划生产y辆汽车,请你根据题意填空,并列出方程组求x与y的值。
(1)若每天生产35辆,在预定期限x天内可生产__________辆,比计划产量y辆汽车__________(“多”或“少”)生产10辆,则可得二元一次方程______________________。
(2)若每天生产40辆,在预定期限x天内可生产__________辆,比计划产量y__________(填“多”或“少”)生产20辆,则可列二元一次方程_________________________。
(3)列方程组_________________________,并解得________。
通过预习本节内容你未解决的问题有:
.
自我评价: 小组评价: 教师评价:
《实际问题和二元一次方程(1)问题生成——评价单》
请同学们在预习的基础上,将生成的问题充分交流后,在单位时间内完成下列题目,并准备多元化展示.
带着问题走进丰富多彩的数学世界
问题一
甲、乙两种作物的单位面积产量的比是2:3,现有一块面积17公顷的土地,要在这块土地上种植这两种作物,且使甲、乙两种作物的总产量的比是3:4,甲、乙两种作物的种植面积分别是多少
问题二:
据统计资料,甲、乙两种作物的单位面积产量的比是1:1.5,现要在一块长200 m,宽100 m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是3:4(结果取整数)
问题1:动手画一画,可能有哪些划分方案 分割线的位置有哪些条件决定
问题2 利用第一种分割方法,如何解这个应用题
问题3 利用第二种分割方法,如何解这个应用题
问题三:
学生在手工实践课中,遇到这样一个问题:要用20张白卡纸制作包装纸盒,每张白卡纸可以做盒身2个,或者做盒底盖3个,如果1个盒身和2个盒底盖可以做成一个包装纸盒,那么能否将这些白卡纸分成两部分,一部分做盒身,一部分做盒底盖,使做成的盒身和盒底盖正好配套?请你设计一种分法.
小组评价: 教师评价:
《实际问题和二元一次方程(2)问题训练——评价单》
设计者: 班级: 姓名:
我要飞得更高
【基础达标】
1、某纸品厂要制作如图1所示的甲、乙两种无盖的长方体小盒,该厂利用边角料裁出了长方形和正方形两种纸片,其中长方形纸片的宽与正方形纸片的边长相等,现将150张正方形纸片和300个长方形纸片用来制作这两种小盒(不计连结部分)可以做甲、乙两种小盒各多少个?
2、去年甲、乙两人总收入之比是8∶7,总支出之比是18∶17,已知在这一年里甲结余了1200元,乙结余了800元,求甲、乙两人去年的总收入各是多少?
3、一个长方形,它的长减少4cm,宽增加2cm,所得的是一个正方形,它的面积与长方形的面积相等,求原长方形的长与宽。
解:设长方形的长为xcm,宽为ycm,由题意得:
【拓展提升】
4、小龙在拼图时,发现8个一样大的小长方形,恰好可以拼成一个大长方形,如图甲所示,
陈晔看见了说“我来试一试”,结果陈晔七拼八凑,拼成一个如图乙的正方形,中间留下一个洞,恰好是边长2mm的小正方形,你能算出小长方形的长和宽吗?
《实际问题和二元一次方程(2)问题导读——评价单》答案
1.,解得 填表略
2.(1)35x 少 35x+10=y
(2)40x 多 40x-20=y
(3),
《实际问题和二元一次方程(2)问题训练——评价单》答案
1、解:设可制作甲种小盒x个,乙种小盒y个.因为一个甲种小盒需一张正方形纸片,4张长方形纸片;一个乙种纸盒需2张正方形纸片和3张长方形纸片,从而寻找相等关系列出方程组解之.
由题意可知:解得
答:可制作甲种小盒30个,乙种小盒60个.
2、4800 4200
3、解:设长方形的长为xcm,宽为ycm,由题意得:
解得
答:长方形的长为8cm,宽为2cm,由题意得:
4、解:设小长方形的长为xcm,宽为ycm.
解得
答:设小长方形的长为10cm,宽为6cm.
本节内容是在学生掌握了二元一次方程组的解法,能列二元一次方程组解较简单的应用题的基础上安排的,其中的“牛饲料问题”“种植计划问题”“成本与产出问题”是具有一定综合性的问题,涉及到估算与精确计算的比较、开放地探索设计方案、根据图表信息列方程组等问题形式.
分析数量关系列出方程组是学习的难点,能正确规范的解决各种各样的实际问题是学习的重点,其中列出方程组如何解是容易忽视的环节,要加强运算速度、准确度的训练,努力做到会的题目保证做对.
【重点、难点】
教学重点:正确理解题目中关键语句的含义,找出等量关系,列二元一次方程组
教学难点:设辅助未知量,用式子正确表示题目中的等量关系
【教学目标】
知识与技能目标:
1、会根据具体问题中的数量关系,经过自主探索、互相交流,列出二元一次方程组并求解,养成对所得结果进行检验的意识;
2、能熟练地列二元一次方程组解决简单的实际问题;
3、通过将实际问题中的数量关系转化为二元一次方程组,体会数学化的过程,提高用数学分析和解决问题的能力。
过程与方法目标:
经历探索、研究、交流的过程,将实际情景中的数量关系抽象出来。
情感与态度目标:
通过实际问题,感受二元一次方程组的广泛应用,加深对数学模型的认识,增强数学的应用意识。
【学生分析】
由于本节需要探究的问题比较复杂,所以学生感到学习难度较大,所以引导学生分析问题就成了重中之重,限于学生的年龄特点和知识积累的量太少,应循序渐进,由易到难,由简单到复杂,避免是学生产生厌学心理。
【设计理念】
1.尊重学生的心里发展的特点,利用情境教学,来调动学生的学习积极性。
2.加强同学之间的合作,通过学生的交流、合作,培养学生的团结意识。
【教学方法】
引导学生课前用好《问题导读---评价单》,对所学知识进行提前预习,找出难理解的问题,以便上课更有针对性。
通过创设情境,将复杂的问题适当分解,用问题引导学生积极思考、努力探索.教学过程实际上就是系列问题探究、解决的过程,学生在教师指导下以问题解决为中心,通过自主探索、合作交流完成各项教学任务,在探索中获得新知,发展能力.引导学生充分利用《问题生成---评价单》。
然后辅之《问题训练---评价单》进行课堂知识的巩固和验证。
【教师课前准备】
《问题导读---评价单》、《问题生成---评价单》、《问题训练---评价单》
【教学过程设计】
问题与情境 师生行为 设计意图
(一)创设情境前面我们初步体验了用方程组解决实际问题的全过程,其实生产、生活中还有许多问题也能用方程组解决.甲、乙两种作物的单位面积产量的比是2:3,现有一块面积17公顷的土地,要在这块土地上种植这两种作物,且使甲、乙两种作物的总产量的比是3:4,甲、乙两种作物的种植面积分别是多少 (二)、探索新知,讲授新课教材106页探究2据统计资料,甲、乙两种作物的单位面积产量的比是1:1.5,现要在一块长200 m,宽100 m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是3:4(结果取整数) 问题1:动手画一画,可能有哪些划分方案 分割线的位置有哪些条件决定 问题2 利用第一种分割方法,如何解这个应用题 问题3 利用第二种分割方法,如何解这个应用题 (三)拓展探究,综合应用学生在手工实践课中,遇到这样一个问题:要用20张白卡纸制作包装纸盒,每张白卡纸可以做盒身2个,或者做盒底盖3个,如果1个盒身和2个盒底盖可以做成一个包装纸盒,那么能否将这些白卡纸分成两部分,一部分做盒身,一部分做盒底盖,使做成的盒身和盒底盖正好配套?请你设计一种分法.(四)、接受考验发放《问题训练---评价单》,学生独立完成上面的练习题(五)反思回顾问题1:本节课你学习了什么 问题2:本节课你有哪些收获 问题3:通过今天的学习,你想进一步探究的问题是什么 课前让学生利用《问题导读---评价单》进行预习,以便对本节课有一个更清晰的认识。解:设甲种作物的单位面积产量为2a,种植面积为x公顷,乙种作物的单位面积产量为3a,种植面积分别为y公顷,根据题意得x+y=172ax:3ay=3:4解得 x=9y=8答:甲、乙两种作物的种植面积分别是9公顷,8公顷教学说明:教师提出问题,学生尝试解答,两名学生板演,结合板演订正,提醒学生注意准确理解关键词语“甲、乙两种作物的单位面积产量的比是2:3”“甲、乙两种作物的总产量的比是3:4”的含义发放《问题生成---评价单》,然后分组讨论上面教师出示的问题,并进行归纳和整理,得出结论,然后请小组代表发言。然后学生整理方程写出规范的解题过程多角度分析问题,多策略解决问题,提高思维的发散性。学生通过动手操作、动脑思考、讨论交流,初步明确了以下问题(1)有两种方法分割长方形(2)分割线的位置要通过计算确定.提示:将本题与准备题比较一下,有哪些方面可以借鉴 如何表示分割后两块地的面积 分析:甲、乙两种作物的单位面积产量的分别为a,1.5a若按如图所示的方案种植,甲、乙两种作物的种植区域分别为长方形AEFD和BCFE.设AE=xm,BE=ym,则甲、乙两种作物的种植面积分别是100xm2,100ym2 甲、乙两种作物的产量分别是100ax,100y×1.5a,根据题意,列方程组为 x+y=200100ax:100y×1.5a=3:4整理得 x+y=2008x=9y解这个方程组得于是可得如下分割方案:过长方形土地的长边上离一端约106 m处,把这块地分为两个长方形.较大一块地种甲作物,较小一块地种乙作物.(教学说明:学生在明确思路的基础上写出解答过程,请一名同学板演,教师对有困难的学生进行指导.学生做完之后先相互交流,教师结合板书简要点评,学生及时订正)要求学生仿照第一种方法写出解答过程,由于类似于前面的解题思路,让学生独立完成,教师对有困难的学生给与指导。解:如图,甲、乙两种作物的种植区域分别为长方形EFCD和ABFE设DE =xm, AE = ym, 根据题意得x+y=100200ax:200y×1.5a=3:4解得 x≈53y≈47于是可得第二种分割方案:过长方形土地的短边上离一端约53 m处,把这块地分为两个长方形.较大一块地种甲作物,较小一块地种乙作物.按以下步骤展开问题的讨论:(l)学生独立思考,构建数学模型. (2)小组讨论达成共识.(3)学生板书讲解.(4)对方程组的解进行探究和讨论,从而得到实际问题的结果.(5)针对以上结论,你能再提出几个探索性问题吗?从不同角度设计练习,巩固学生所学,然后教师给予评价,把出现问题多的题目,给予重点讲解。学生口述本节课所学的内容。师生共同回顾小结。要求学生课后规范作业。 由于探究2种的问题学生较陌生,并且难度较大,所以先设计一个较简单的题目作铺垫,一方面让学生熟悉常用的数量关系,另一方面熟悉列方程解应用题的一般步骤,同时分散探究2的难点引导学生用画图的方式探寻解题思路,使学生先从总体上明确要做什么,然后考虑怎样做的问题教学说明:教师提出问题,让学生讨论交流,在此过程中可以逐步理解题意,找到解决问题的方法设计说明:在学生完成热身练习的基础上,结合图形就能顺利列出方程,之所以要求学生写出规范的解答过程,是因为找到思路只是完成了第一步,能否彻底解决问题还需要计算、表达等多方面的能力,所以务必在这个环节上对学生严格要求一方面可以检验学习效果如何,另一方面可以让学生进一步体会方法的重要性,将举一反三落到实处以学生学习生活中遇到的问题展开讨论,巩固用二元一次方程组解决实际问题的一般过程,并不断提高分析问题的能力.安排开放题,以利于培养学生探索精神和创新意识.通过练习题的练习可以规范解题步骤,培养学生有条理地思考、表达的习惯。以上设计再次通过对三个问题的思考引导学生回顾自己的学习过程,畅所欲言,加强反思、提炼及知识的归纳,纳入自己的知识结构
教学反思
1.本节主要学习用画图的方法分析数量关系,通过列二元一次方程组设计方案.2.主要用到的思想方法是方程思想:将实际问题转化成二元一次方程组解决3.注意的问题:(1)认真审题,准确理解关键语句的含义.(2)解出方程组时要选择适当的方法,提高运算速度、准确度..(3)从多角度寻求解决问题的途径.
《实际问题和二元一次方程(2)问题导读——评价单》
设计者: 班级: 姓名:
知识与技能目标:
1、会根据具体问题中的数量关系,经过自主探索、互相交流,列出二元一次方程组并求解,养成对所得结果进行检验的意识;
2、能熟练地列二元一次方程组解决简单的实际问题;
3、通过将实际问题中的数量关系转化为二元一次方程组,体会数学化的过程,提高用数学分析和解决问题的能力。
过程与方法目标:
经历探索、研究、交流的过程,将实际情景中的数量关系抽象出来。
情感与态度目标:
通过实际问题,感受二元一次方程组的广泛应用,加深对数学模型的认识,增强数学的应用意识。
为你导航
1.某市现有42万人口,计划一年后城镇人口增加0.8%,农村人口增加1.1%,这样全市人口将增加1%,求这个市现在的城镇人口与农村人口?
设城镇人口是x万,农村人口是y万,根据题意填写下表,并列出方程组求x、y的值。
城镇 农村 全市
现有人数(万人) x y 42
一年后增加人口(万人)
2.某汽车制造厂接受了在预定期限内生产一批汽车的任务,如果每天生产35辆,则差10辆才能完成任务;如果每天生产40辆,则可超额生产20辆。试求预定期限是多少天?计划生产多少辆汽车?
若设预定期限为x天,计划生产y辆汽车,请你根据题意填空,并列出方程组求x与y的值。
(1)若每天生产35辆,在预定期限x天内可生产__________辆,比计划产量y辆汽车__________(“多”或“少”)生产10辆,则可得二元一次方程______________________。
(2)若每天生产40辆,在预定期限x天内可生产__________辆,比计划产量y__________(填“多”或“少”)生产20辆,则可列二元一次方程_________________________。
(3)列方程组_________________________,并解得________。
通过预习本节内容你未解决的问题有:
.
自我评价: 小组评价: 教师评价:
《实际问题和二元一次方程(1)问题生成——评价单》
请同学们在预习的基础上,将生成的问题充分交流后,在单位时间内完成下列题目,并准备多元化展示.
带着问题走进丰富多彩的数学世界
问题一
甲、乙两种作物的单位面积产量的比是2:3,现有一块面积17公顷的土地,要在这块土地上种植这两种作物,且使甲、乙两种作物的总产量的比是3:4,甲、乙两种作物的种植面积分别是多少
问题二:
据统计资料,甲、乙两种作物的单位面积产量的比是1:1.5,现要在一块长200 m,宽100 m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是3:4(结果取整数)
问题1:动手画一画,可能有哪些划分方案 分割线的位置有哪些条件决定
问题2 利用第一种分割方法,如何解这个应用题
问题3 利用第二种分割方法,如何解这个应用题
问题三:
学生在手工实践课中,遇到这样一个问题:要用20张白卡纸制作包装纸盒,每张白卡纸可以做盒身2个,或者做盒底盖3个,如果1个盒身和2个盒底盖可以做成一个包装纸盒,那么能否将这些白卡纸分成两部分,一部分做盒身,一部分做盒底盖,使做成的盒身和盒底盖正好配套?请你设计一种分法.
小组评价: 教师评价:
《实际问题和二元一次方程(2)问题训练——评价单》
设计者: 班级: 姓名:
我要飞得更高
【基础达标】
1、某纸品厂要制作如图1所示的甲、乙两种无盖的长方体小盒,该厂利用边角料裁出了长方形和正方形两种纸片,其中长方形纸片的宽与正方形纸片的边长相等,现将150张正方形纸片和300个长方形纸片用来制作这两种小盒(不计连结部分)可以做甲、乙两种小盒各多少个?
2、去年甲、乙两人总收入之比是8∶7,总支出之比是18∶17,已知在这一年里甲结余了1200元,乙结余了800元,求甲、乙两人去年的总收入各是多少?
3、一个长方形,它的长减少4cm,宽增加2cm,所得的是一个正方形,它的面积与长方形的面积相等,求原长方形的长与宽。
解:设长方形的长为xcm,宽为ycm,由题意得:
【拓展提升】
4、小龙在拼图时,发现8个一样大的小长方形,恰好可以拼成一个大长方形,如图甲所示,
陈晔看见了说“我来试一试”,结果陈晔七拼八凑,拼成一个如图乙的正方形,中间留下一个洞,恰好是边长2mm的小正方形,你能算出小长方形的长和宽吗?
《实际问题和二元一次方程(2)问题导读——评价单》答案
1.,解得 填表略
2.(1)35x 少 35x+10=y
(2)40x 多 40x-20=y
(3),
《实际问题和二元一次方程(2)问题训练——评价单》答案
1、解:设可制作甲种小盒x个,乙种小盒y个.因为一个甲种小盒需一张正方形纸片,4张长方形纸片;一个乙种纸盒需2张正方形纸片和3张长方形纸片,从而寻找相等关系列出方程组解之.
由题意可知:解得
答:可制作甲种小盒30个,乙种小盒60个.
2、4800 4200
3、解:设长方形的长为xcm,宽为ycm,由题意得:
解得
答:长方形的长为8cm,宽为2cm,由题意得:
4、解:设小长方形的长为xcm,宽为ycm.
解得
答:设小长方形的长为10cm,宽为6cm.
