人教新课标版七下多边形基础一案三单设计
文档属性
| 名称 | 人教新课标版七下多边形基础一案三单设计 |  | |
| 格式 | zip | ||
| 文件大小 | 46.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-18 20:10:56 | ||
图片预览


文档简介
多边形教案
【教材分析】
多边形是以三角形为基础,利用类比和化归思想探索多边形的有关概念,多边形的内角和与外角和公式,使学生体会类比与化归思想在数学中的应用.
多边形的探索在三角形的基础上进行,学生以前所学的正方形、长方形等也都是多边形,探索这些图形的性质都可以分割成几个三角形进行解决.所以不仅要类比探索三角形的方法来探索多边形,还要将多边形分解成三角形进行研究,这就是本节课所涉及的类比思想与化归思想,进而培养学生发现问题和解决问题的能力,学会将新知识转化为已学的旧知识进行解决问题的方法.
【教学目标】
知识目标
以三角形为基础,了解多边形的定义及相关概念(多边形的内角、外角、对角线 等);了解多边形的对角线与边数之间的关系;了解凸四边形的定义;了解正多边形的概念;
过程与方法
1、通过把多边形转化成三角形体会转化思想在几何中的运用,体会从特殊到一般的认识问题的方法;
2、尝试从不同的角度寻求解决问题的方法并能有效地解决问题;
情感目标
通过猜想、推理等数学活动,感受数学活动充满着探索以及数学结论的确定,提高学习热情。
【教学重点】
多边形和正多边形的概念
【教学难点】
对多边形和正多边形的概念的正确理解;多边形的对角线与边数之间的关系
【教学方法】
课前布置学生根据问题导读评价单进行预习,找出难以理解的问题,以增强课上的听课效率。课堂中利用问题生成评价单进行分组讨论,培养学生的合作技能和合作意识,提高学生独立解决问题的能力。最后利用问题训练评价单对所学的知识进行考核,查漏补缺。
【学生分析】
1、学生的认知水平有限,需要给学生呈现一些感性的图片和材料等
2、大部分学生还存在着依赖性,不愿意自己探究知识,没有好的学习习惯,还要教师在今后的学习中进行渗透。
【设计理念】
创设情境,从生活中常见的图形出发,激发学生兴趣,引导学生发现并解决问题.教学环节的设计与展开,都要关注学生的交流与思想活动,引导学生利用类比和化归的方法解决问题,体会数学思想的重要性.建议本节课使用多媒体进行辅助教学.
【教师课前准备】
《问题导读---评价单》、《问题生成---评价单》、《问题训练---评价单》
【教学过程设计】
问题与情境 师生活动 设计意图
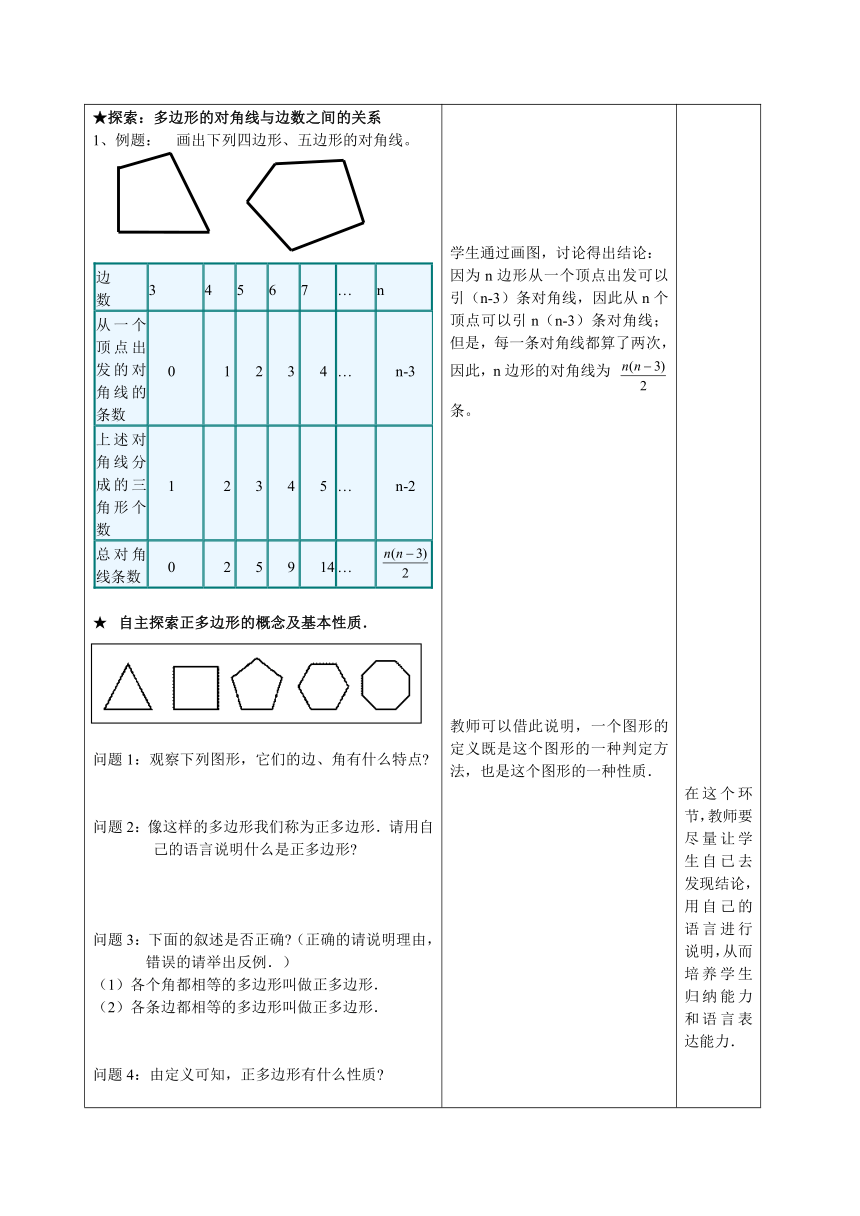
创设情景,引入新课问题1:观察下面的图片,你能找到哪些我们熟悉的图形 问题2:这些图形我们要给出一个统一的名称,称它们为多边形.那么到底什么是多边形呢 合作交流,探索新知★观察多边形的构成,类比三角形的有关概念探索多边形的有关概念问题1:观察画多边形的过程,类比三角形的概念,你能说出什么是多边形吗 问题2:根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角和对角线.问题3:三角形有对角线吗 为什么 问题4:回想三角形的表示方法,这个多边形应如何表示 问题5:如图所示,观察两个图形,找出相同点和不同点.★探索:多边形的对角线与边数之间的关系1、例题: 画出下列四边形、五边形的对角线。边 数34567…n从一个顶点出发的对角线的条数 0 1 2 3 4… n-3上述对角线分成的三角形个数 1 2 3 4 5… n-2总对角线条数 0 2 5 9 14… 自主探索正多边形的概念及基本性质.问题1:观察下列图形,它们的边、角有什么特点 问题2:像这样的多边形我们称为正多边形.请用自己的语言说明什么是正多边形 问题3:下面的叙述是否正确 (正确的请说明理由,错误的请举出反例.)(1)各个角都相等的多边形叫做正多边形.(2)各条边都相等的多边形叫做正多边形.问题4:由定义可知,正多边形有什么性质 轻松过关发放《问题训练评价单》,让学生独立完成其练习题归纳总结,形成体系 问题1:本节课你学习了什么 问题2:本节课你有哪些收获 问题3:通过今天的学习,你想进一步探究的问题是什么 上课之前先检查学生对《问题导读评价单》的完成情况学生回答:三角形、长方形、正方形、梯形、平行四边形、五边形、六边形、八边形等.发放《问题生成评价单》,然后小组根据其提出的问题进行讨论,交流各组的意见,向老师请求帮助。发现问题的思考方法。学生交流多边形概念并进行总结教师讲解:如果一个多边形有n条边,我们就叫它n边形.但要注意,n所代表的数字必须是汉字中的数字,如三角形、六边形、十边形、十七边形等.但当问题问这个n边形有几条边时,我们可以用阿拉伯数字说明这个n边形有3条边、6条边等.学生讨论回答:组成多边形的线段叫多边形的边;相邻两边的交点叫做它的顶点;相邻两边的夹角叫做它的内角;多边形的边与它邻边的延长线组成的角叫做多边形的外角;连接多边形不相邻的两个顶点的线段叫做多边形的对角线.学生回答:三角形没有对角线,因为三角形只有三个顶点,而这三个顶点是两两相邻的,它没有不相邻的顶点,所以没有对角线.学生回答:首先给每一个顶点标上一个大写字母,然后写出这个图形是几边形,最后再以一个字母为起点,沿顺时针或逆时针方向将字母按顺序写出.如:四边形ABCD,五边形ABCDE,n边形A1A2A3…An等.学生回答:相同点是这两个图形都有五条边,都是五边形.不同点是,左边图形有一个内角大于180°,而右边图形的每个内角都小于180°.教师讲解:如图,画出多边形一边所在直线,我们发现左边的图形分布在直线两侧,而右边图形都在直线的同侧.那么,像这样,画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形;如果整个图形不在这条直线的同一侧,那么这个多边形就是凹多边形.而在本节我们只讨论凸多边形学生通过画图,讨论得出结论:因为n边形从一个顶点出发可以引(n-3)条对角线,因此从n个顶点可以引n(n-3)条对角线;但是,每一条对角线都算了两次,因此,n边形的对角线为 条。教师可以借此说明,一个图形的定义既是这个图形的一种判定方法,也是这个图形的一种性质.围绕三个问题,师生以谈话交流的形式,共同总结本节课的学习收获。 通过展示现实生活的各种图片,让学生从常见图形入手,降低知识难度,激发学生自主学习的兴趣和积极性,并引入新课.设计说明:三角形是多边形中最简单的一个图形,所以要类比三角形的有关概念探索多边形的有关概念.本环节充分体现了类比思想在数学中的应用.所以在教学时,教师要让学生类比着三角形的有关概念来总结多边形的有关概念.在这个环节,教师要尽量让学生自已去发现结论,用自己的语言进行说明,从而培养学生归纳能力和语言表达能力.通过基础练习,加深对新知识的理解和运用,形成初步技能.以上设计再次通过对三个问题的思考引导学生回顾自己的学习过程,畅所欲言,加强反思、提炼及知识的归纳,纳入自己的知识结构
《多边形问题导读——评价单》
设计者: 班级: 姓名:
【教学目标】
知识目标
以三角形为基础,了解多边形的定义及相关概念(多边形的内角、外角、对角线 等);了解多边形的对角线与边数之间的关系;了解凸四边形的定义;了解正多边形的概念;
过程与方法
1、通过把多边形转化成三角形体会转化思想在几何中的运用,体会从特殊到一般的认识问题的方法;
2、尝试从不同的角度寻求解决问题的方法并能有效地解决问题;
情感目标
通过猜想、推理等数学活动,感受数学活动充满着探索以及数学结论的确定,提高学习热情。
【教学重点】
多边形和正多边形的概念
【教学难点】
对多边形和正多边形的概念的正确理解;多边形的对角线与边数之间的关系
为你导航
1、在平面内,由一些线段________________相接组成的________叫做多边形。
2、多边形_________组成的角叫做多边形的内角。
3、多边形的边与它的的邻边的__________组成的角叫做多边形的外角。
4、连接多边形_________的两个顶点的线段叫做多边形的对角线。
5、多边形用表示它的各顶点的大写字母来表示,表示多边形必须按 书写,可按顺时针或逆时针顺序。
6、_________都相等,_________都相等的多边形叫做正多边形。
7、画出多边形的任何一条边所在的直线,如果整个图形都在这条直线的同一侧,那么这样的多边形称为
8从n边形的一个顶点出发可以画_____条对角线,把n边形分成了____个三角形;n边形共有_____条对角线。
9、过m边形的一个顶点有7条对角线,n边形没有对角线,k边形有2条对角线,则(m-n-k)=________.
10、过十边形的一个顶点可作出____条对角线,把十边形分成了___个三角形。
通过预习本节内容你未解决的问题有:
.
自我评价: 小组评价: 教师评价:
《多边形问题生成——评价单》
设计者: 班级: 姓名:
请同学们在预习的基础上,将生成的问题充分交流后,在单位时间内完成下列题目,并准备多元化展示.
带着问题走进丰富多彩的数学世界
问题一:
问题1:观察画多边形的过程,类比三角形的概念,你能说出什么是多边形吗
问题2:根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角和对角线.
问题3:三角形有对角线吗 为什么
问题4:回想三角形的表示方法,这个多边形应如何表示
问题5:如图所示,观察两个图形,找出相同点和不同点.
问题二:
问题1:例题: 画出下列四边形、五边形的对角线。
问题2:因为n边形从一个顶点出发可以引 条对角线,因此从n个顶点可以引 条对角线;但是,每一条对角线都算了两次,因此,n边形的对角线为 条。
问题三:
问题1:观察下列图形,它们的边、角有什么特点
问题2:像这样的多边形我们称为正多边形.请用自己的语言说明什么是正多边形
问题3:下面的叙述是否正确 (正确的请说明理由,错误的请举出反例.)
(1)各个角都相等的多边形叫做正多边形.
(2)各条边都相等的多边形叫做正多边形.
问题4:由定义可知,正多边形有什么性质
自我评价: 小组评价: 教师评价:
《多边形问题训练——评价单》
设计者: 班级: 姓名:
我要飞得更高
基础达标
1、下列图形中,是正多边形的是( )
A直角三角形 B等腰三角形 C长方形 D正方形
2、九边形的对角线有( )
A 25条 B 31条 C 27条 D 30条
3、右图中四边形共有( )
A.3个 B.4个 C.5个 D.6个
4、在有对角线的多边形中,边数最少的是____边形,它共有____条对角线.
5、三十边形共有____条对角线。
6、一个多边形的对角线的条数等于它的边数的4倍,求这个多边形的边数。
能力拓展:
7、从8边形的一个顶点可以引____条对角线,它们将8边形分成 _____个三角形。利用三角形内角和1800,推出8边形内角和。写出推理过程。
自我评价: 小组评价: 教师评价:
《多边形问题导读——评价单》答案
首位顺次相接 2、相邻两边 3、延长线 4、不相邻 5、顺序
6、各个角、各条边 7、凸多边形 8、n-3 n-2
9、2 10、7 8
《多边形问题训练——评价单》答案
基础达标
1、D 2、C 3、D 4、四边形 两条5、27 6、11
能力拓展
5 6
因为从8边形的一个顶点可以引5条条对角线,这五条对角线将8边形分成5个三角形。利又因为三角形内角和1800,
所以这五个三角形的内角和为180°*6=1080°
而这五个三角形的内角和即为八边形的内角和。
【教材分析】
多边形是以三角形为基础,利用类比和化归思想探索多边形的有关概念,多边形的内角和与外角和公式,使学生体会类比与化归思想在数学中的应用.
多边形的探索在三角形的基础上进行,学生以前所学的正方形、长方形等也都是多边形,探索这些图形的性质都可以分割成几个三角形进行解决.所以不仅要类比探索三角形的方法来探索多边形,还要将多边形分解成三角形进行研究,这就是本节课所涉及的类比思想与化归思想,进而培养学生发现问题和解决问题的能力,学会将新知识转化为已学的旧知识进行解决问题的方法.
【教学目标】
知识目标
以三角形为基础,了解多边形的定义及相关概念(多边形的内角、外角、对角线 等);了解多边形的对角线与边数之间的关系;了解凸四边形的定义;了解正多边形的概念;
过程与方法
1、通过把多边形转化成三角形体会转化思想在几何中的运用,体会从特殊到一般的认识问题的方法;
2、尝试从不同的角度寻求解决问题的方法并能有效地解决问题;
情感目标
通过猜想、推理等数学活动,感受数学活动充满着探索以及数学结论的确定,提高学习热情。
【教学重点】
多边形和正多边形的概念
【教学难点】
对多边形和正多边形的概念的正确理解;多边形的对角线与边数之间的关系
【教学方法】
课前布置学生根据问题导读评价单进行预习,找出难以理解的问题,以增强课上的听课效率。课堂中利用问题生成评价单进行分组讨论,培养学生的合作技能和合作意识,提高学生独立解决问题的能力。最后利用问题训练评价单对所学的知识进行考核,查漏补缺。
【学生分析】
1、学生的认知水平有限,需要给学生呈现一些感性的图片和材料等
2、大部分学生还存在着依赖性,不愿意自己探究知识,没有好的学习习惯,还要教师在今后的学习中进行渗透。
【设计理念】
创设情境,从生活中常见的图形出发,激发学生兴趣,引导学生发现并解决问题.教学环节的设计与展开,都要关注学生的交流与思想活动,引导学生利用类比和化归的方法解决问题,体会数学思想的重要性.建议本节课使用多媒体进行辅助教学.
【教师课前准备】
《问题导读---评价单》、《问题生成---评价单》、《问题训练---评价单》
【教学过程设计】
问题与情境 师生活动 设计意图
创设情景,引入新课问题1:观察下面的图片,你能找到哪些我们熟悉的图形 问题2:这些图形我们要给出一个统一的名称,称它们为多边形.那么到底什么是多边形呢 合作交流,探索新知★观察多边形的构成,类比三角形的有关概念探索多边形的有关概念问题1:观察画多边形的过程,类比三角形的概念,你能说出什么是多边形吗 问题2:根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角和对角线.问题3:三角形有对角线吗 为什么 问题4:回想三角形的表示方法,这个多边形应如何表示 问题5:如图所示,观察两个图形,找出相同点和不同点.★探索:多边形的对角线与边数之间的关系1、例题: 画出下列四边形、五边形的对角线。边 数34567…n从一个顶点出发的对角线的条数 0 1 2 3 4… n-3上述对角线分成的三角形个数 1 2 3 4 5… n-2总对角线条数 0 2 5 9 14… 自主探索正多边形的概念及基本性质.问题1:观察下列图形,它们的边、角有什么特点 问题2:像这样的多边形我们称为正多边形.请用自己的语言说明什么是正多边形 问题3:下面的叙述是否正确 (正确的请说明理由,错误的请举出反例.)(1)各个角都相等的多边形叫做正多边形.(2)各条边都相等的多边形叫做正多边形.问题4:由定义可知,正多边形有什么性质 轻松过关发放《问题训练评价单》,让学生独立完成其练习题归纳总结,形成体系 问题1:本节课你学习了什么 问题2:本节课你有哪些收获 问题3:通过今天的学习,你想进一步探究的问题是什么 上课之前先检查学生对《问题导读评价单》的完成情况学生回答:三角形、长方形、正方形、梯形、平行四边形、五边形、六边形、八边形等.发放《问题生成评价单》,然后小组根据其提出的问题进行讨论,交流各组的意见,向老师请求帮助。发现问题的思考方法。学生交流多边形概念并进行总结教师讲解:如果一个多边形有n条边,我们就叫它n边形.但要注意,n所代表的数字必须是汉字中的数字,如三角形、六边形、十边形、十七边形等.但当问题问这个n边形有几条边时,我们可以用阿拉伯数字说明这个n边形有3条边、6条边等.学生讨论回答:组成多边形的线段叫多边形的边;相邻两边的交点叫做它的顶点;相邻两边的夹角叫做它的内角;多边形的边与它邻边的延长线组成的角叫做多边形的外角;连接多边形不相邻的两个顶点的线段叫做多边形的对角线.学生回答:三角形没有对角线,因为三角形只有三个顶点,而这三个顶点是两两相邻的,它没有不相邻的顶点,所以没有对角线.学生回答:首先给每一个顶点标上一个大写字母,然后写出这个图形是几边形,最后再以一个字母为起点,沿顺时针或逆时针方向将字母按顺序写出.如:四边形ABCD,五边形ABCDE,n边形A1A2A3…An等.学生回答:相同点是这两个图形都有五条边,都是五边形.不同点是,左边图形有一个内角大于180°,而右边图形的每个内角都小于180°.教师讲解:如图,画出多边形一边所在直线,我们发现左边的图形分布在直线两侧,而右边图形都在直线的同侧.那么,像这样,画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形;如果整个图形不在这条直线的同一侧,那么这个多边形就是凹多边形.而在本节我们只讨论凸多边形学生通过画图,讨论得出结论:因为n边形从一个顶点出发可以引(n-3)条对角线,因此从n个顶点可以引n(n-3)条对角线;但是,每一条对角线都算了两次,因此,n边形的对角线为 条。教师可以借此说明,一个图形的定义既是这个图形的一种判定方法,也是这个图形的一种性质.围绕三个问题,师生以谈话交流的形式,共同总结本节课的学习收获。 通过展示现实生活的各种图片,让学生从常见图形入手,降低知识难度,激发学生自主学习的兴趣和积极性,并引入新课.设计说明:三角形是多边形中最简单的一个图形,所以要类比三角形的有关概念探索多边形的有关概念.本环节充分体现了类比思想在数学中的应用.所以在教学时,教师要让学生类比着三角形的有关概念来总结多边形的有关概念.在这个环节,教师要尽量让学生自已去发现结论,用自己的语言进行说明,从而培养学生归纳能力和语言表达能力.通过基础练习,加深对新知识的理解和运用,形成初步技能.以上设计再次通过对三个问题的思考引导学生回顾自己的学习过程,畅所欲言,加强反思、提炼及知识的归纳,纳入自己的知识结构
《多边形问题导读——评价单》
设计者: 班级: 姓名:
【教学目标】
知识目标
以三角形为基础,了解多边形的定义及相关概念(多边形的内角、外角、对角线 等);了解多边形的对角线与边数之间的关系;了解凸四边形的定义;了解正多边形的概念;
过程与方法
1、通过把多边形转化成三角形体会转化思想在几何中的运用,体会从特殊到一般的认识问题的方法;
2、尝试从不同的角度寻求解决问题的方法并能有效地解决问题;
情感目标
通过猜想、推理等数学活动,感受数学活动充满着探索以及数学结论的确定,提高学习热情。
【教学重点】
多边形和正多边形的概念
【教学难点】
对多边形和正多边形的概念的正确理解;多边形的对角线与边数之间的关系
为你导航
1、在平面内,由一些线段________________相接组成的________叫做多边形。
2、多边形_________组成的角叫做多边形的内角。
3、多边形的边与它的的邻边的__________组成的角叫做多边形的外角。
4、连接多边形_________的两个顶点的线段叫做多边形的对角线。
5、多边形用表示它的各顶点的大写字母来表示,表示多边形必须按 书写,可按顺时针或逆时针顺序。
6、_________都相等,_________都相等的多边形叫做正多边形。
7、画出多边形的任何一条边所在的直线,如果整个图形都在这条直线的同一侧,那么这样的多边形称为
8从n边形的一个顶点出发可以画_____条对角线,把n边形分成了____个三角形;n边形共有_____条对角线。
9、过m边形的一个顶点有7条对角线,n边形没有对角线,k边形有2条对角线,则(m-n-k)=________.
10、过十边形的一个顶点可作出____条对角线,把十边形分成了___个三角形。
通过预习本节内容你未解决的问题有:
.
自我评价: 小组评价: 教师评价:
《多边形问题生成——评价单》
设计者: 班级: 姓名:
请同学们在预习的基础上,将生成的问题充分交流后,在单位时间内完成下列题目,并准备多元化展示.
带着问题走进丰富多彩的数学世界
问题一:
问题1:观察画多边形的过程,类比三角形的概念,你能说出什么是多边形吗
问题2:根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角和对角线.
问题3:三角形有对角线吗 为什么
问题4:回想三角形的表示方法,这个多边形应如何表示
问题5:如图所示,观察两个图形,找出相同点和不同点.
问题二:
问题1:例题: 画出下列四边形、五边形的对角线。
问题2:因为n边形从一个顶点出发可以引 条对角线,因此从n个顶点可以引 条对角线;但是,每一条对角线都算了两次,因此,n边形的对角线为 条。
问题三:
问题1:观察下列图形,它们的边、角有什么特点
问题2:像这样的多边形我们称为正多边形.请用自己的语言说明什么是正多边形
问题3:下面的叙述是否正确 (正确的请说明理由,错误的请举出反例.)
(1)各个角都相等的多边形叫做正多边形.
(2)各条边都相等的多边形叫做正多边形.
问题4:由定义可知,正多边形有什么性质
自我评价: 小组评价: 教师评价:
《多边形问题训练——评价单》
设计者: 班级: 姓名:
我要飞得更高
基础达标
1、下列图形中,是正多边形的是( )
A直角三角形 B等腰三角形 C长方形 D正方形
2、九边形的对角线有( )
A 25条 B 31条 C 27条 D 30条
3、右图中四边形共有( )
A.3个 B.4个 C.5个 D.6个
4、在有对角线的多边形中,边数最少的是____边形,它共有____条对角线.
5、三十边形共有____条对角线。
6、一个多边形的对角线的条数等于它的边数的4倍,求这个多边形的边数。
能力拓展:
7、从8边形的一个顶点可以引____条对角线,它们将8边形分成 _____个三角形。利用三角形内角和1800,推出8边形内角和。写出推理过程。
自我评价: 小组评价: 教师评价:
《多边形问题导读——评价单》答案
首位顺次相接 2、相邻两边 3、延长线 4、不相邻 5、顺序
6、各个角、各条边 7、凸多边形 8、n-3 n-2
9、2 10、7 8
《多边形问题训练——评价单》答案
基础达标
1、D 2、C 3、D 4、四边形 两条5、27 6、11
能力拓展
5 6
因为从8边形的一个顶点可以引5条条对角线,这五条对角线将8边形分成5个三角形。利又因为三角形内角和1800,
所以这五个三角形的内角和为180°*6=1080°
而这五个三角形的内角和即为八边形的内角和。
