人教新课标版七下多边形的内角和一案三单设计
文档属性
| 名称 | 人教新课标版七下多边形的内角和一案三单设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 81.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-18 00:00:00 | ||
图片预览



文档简介
多边形内角和教案
【教材分析】
本章及本节的地位与作用是本节课“多边形的内角和”作为本章的一个重点,是三角形有关知识的拓展,学习四边形的基础, 公式的运用还充分地体现了图形与客观世界的密切联系。本节课作为第七章第三节,起着承上启下的作用。在内容上,从三角形内角和到多边形内角和,环环相扣,层层递进,这样编排易于激发学生的学习兴趣,很适合学生的认知特点。通过这节课的学习,可以培养学习探索与归纳能力,体会到从简单到复杂,从特殊到一般和转化等重要的思想方法。
【教学目标】
根据新课程标准的要求,课改应体现学生身心发展特点;应有利于引导学生主动探索和发现;有利于进行创造性的教学。因此,我把本节课的教学目标确定为以下三个方面:
知识目标:
①理解多边形内角和公式的推导过程;
②掌握多边形内角和公式的内涵及其运用。
能力目标:
① 培养学生类比归纳、转化的能力;
②培养学生观察分析、猜想和概括的能力。
思想情感目标:
通过体会数学图形的美感,提高审美能力, 树立认识数学来源于生活,又服务于实践的观点。
【重点与难点】
多边形内角和的公式及公式的推导和运用是本节课的重点;
难点是如何引导学生通过自主学习, 探索多边形内角和的公式。
【学生分析】
初中生作为过程的主体,需要通过积极主动的学习,获取丰富的知识技能和行为经验完成学习过程。初中生的一般特征有初中生的年龄、性别、心理发展水平、学习动机、人格因素、生活经验以及社会背景等方面。
【教学方法】
课前布置学生进行预习,根据自己的学习,完成《问题导读评价单》,从而发现本节课存在的难点问题
课上树立以学生为本的思想,通过创设问题情境,利用《问题生成评价单》,启发引导学生观察----分析----猜想----概括,培养学生积极思考,勇于探索的精神,充分发挥其自主能动性。
最后通过问题训练评价单对学生本节课所学的知识点进行验证,做到查漏补缺
【设计理念】
培养学生学习能力的是教学中的关键,所以在教学中注重针对学生的认知规律,指导他们动手操作、交流合作,是学生独立的去发现问题、探索问题和解决问题。
【教师准备】
《问题导读---评价单》、《问题生成---评价单》、《问题训练---评价单》
【教学过程的设计】
问题与情境 师生活动 设计意图
创设情景,引入新课 三角形的内角和等于180°,正方形,长方形的内角和都等于360°,而其他的四边形的内角和是否也等于360度呢?你能利用三角形内角和定理证明四边形的内角和等于360度 吗?合作交流,探索新知1、动手试一试任意画一个四边形,量出它的四个内角,计算它的内角和。并在小组内交流,猜想四边形的内角和。 能否根据已经学过的三角形内角和知识来解决四边形的内角和?然后在小组内交流,找出简单的方法。2、若任意给出一个多边形,如二十边形,要求它的内角和,如果采用上述的度量法,就得量出二十个内角的度数,再计算。这样很麻烦。所以请同学们思考这样一个问题:能不能利用学过的三角形的内角和来解决这个问题?自主探索,得出结论 问题1:对比上面探究四边形内角和的过程,你能得出五边形的内角和?六边形的内角和?问题2:能否采用不同的分割方法来解决问题问题3:n边形的内角和是多少? 轻松过关发放《问题训练评价单》,让学生独立完成其练习题归纳总结,形成体系 1、归纳本节课学习了以下主要内容:(1)探索了n边形的内角和公式(2)学会转化思想 上课之前先检查学生对《问题导读评价单》的完成情况教师给出问题,带领学生进入到思考的情境中.让学生亲身体验数学发现的过程。在教师的引导下得出结论。深入各组,倾听他们的意见。提问个别学生答案。任意画一个四边形四个内角和为360度。如图,画出任意一个四边形的一条对角线,都能将这个四边形分为两个三角形。所以四边形的内角和为360度。发放《问题生成评价单》,然后小组根据其提出的问题进行讨论,交流各组的意见,向老师请求帮助。发现问题的思考方法。引导学生根据问题评价单中的问题进一步探讨五边形、六边形和n边形的内角和的度数。(1)从五边形的一个顶点出发,可以引 条对角线,它们将五边形分为 个三角形,五边形的内角和等于180 °× .(2)从六边形的一个顶点出发,可以引 条对角线,它们将六边形分为 个三角形,六边形的内角和等于180 °× .由此我们可以看出,求多边形的内角和,可以把多边形用对角线分成若开个三角形。利用三角形的内角和求解,而分得的三角形的个数又与从一个顶点引出的对角线的条数有关。利用刚才的思路大家猜想一下,还有其他的方法吗?小组讨论,交流各组的意见,向老师请求帮助。发现问题,思考方法。180°×5-360° =(5-2)×180°=3 ×180°180°×4-180°=(4-1)×180°=3 ×180°从n边形的一个顶点出发,可以引 条对角线,它们将n边形分为 个三角形,n边形的内角和等于180 °× .180°n-360°=(n-2)×180°教师根据学生的回答,给予评价,并在此过程中规范学生的言语表达。训练学生的逻辑表达能力。学生通过比较,订正自己的错误的过程。提问,引导学生进一步巩固对这一节的认识。学生总结不完整,在教师的指导下完成。 依据新课程的理念,从原有的知识下手,提出问题,引出学生思考。通过学生自己动手,让他们积极参加数学活动,主动思考,合作交流。经过交流,教师向学生提供必要的帮助。体现教师是学生学习的,组织者、合作者、参与者。在得出任意四边形的内角和的求法后,再让学生思考五边形、六边形的内角和的求法,旨在让学生能从中找到规律,为后面求N边形的内角和打下基础通过比较,学生的思维得到进一步扩展,以达到举一反三的作用。培养学生的一个重要的思想:转化思想。从特殊到一般的思想。通过练习,学生加深对所学的知识应用。利用多边形的内角和解答,为这一章节的重难点在练习中起到一个突破的作用。让学生在课堂上有时间进行思考,把时间给学生,体现课堂上学生是教学的主体
《多边形内角和问题导读——评价单》
设计者: 班级: 姓名:
教学目标
知识目标:
①理解多边形内角和公式的推导过程;
②掌握多边形内角和公式的内涵及其运用。
能力目标:
① 培养学生类比归纳、转化的能力;
②培养学生观察分析、猜想和概括的能力。
思想情感目标:
通过体会数学图形的美感,提高审美能力, 树立认识数学来源于生活,又服务于实践的观点。
重点与难点
多边形内角和的公式及公式的推导和运用是本节课的重点;
难点是如何引导学生通过自主学习, 探索多边形内角和的公式。
为你导航
1、四边形的内角和为( )
A.180° B.360° C.540° D.720°
2、一个多边形的内角和是720°,这个多边形的边数是( )
A.4 B.5 C.6 D.7
3、在五边形ABCDE中,若∠A=100°,且其余四个内角度数相等,则∠C=( )
A.65° B.100° C.108° D.110°
4、多边形的内角和不可能为( )
A.180° B.680° C.1080° D.1980°
通过预习本节内容你未解决的问题有:
.
自我评价: 小组评价: 教师评价:
《多边形内角和问题生成——评价单》
设计者: 班级: 姓名:
请同学们在预习的基础上,将生成的问题充分交流后,在单位时间内完成下列题目,并准备多元化展示.
带着问题走进丰富多彩的数学世界
问题一:
1、任意画一个四边形,量出它的四个内角,计算它的内角和。并在小组内交流,猜想四边形的内角和。
2、若任意给出一个多边形,如二十边形,要求它的内角和,如果采用上述的度量法,就得量出二十个内角的度数,再计算。这样很麻烦。所以请同学们思考这样一个问题:能不能利用学过的三角形的内角和来解决这个问题?
问题二:
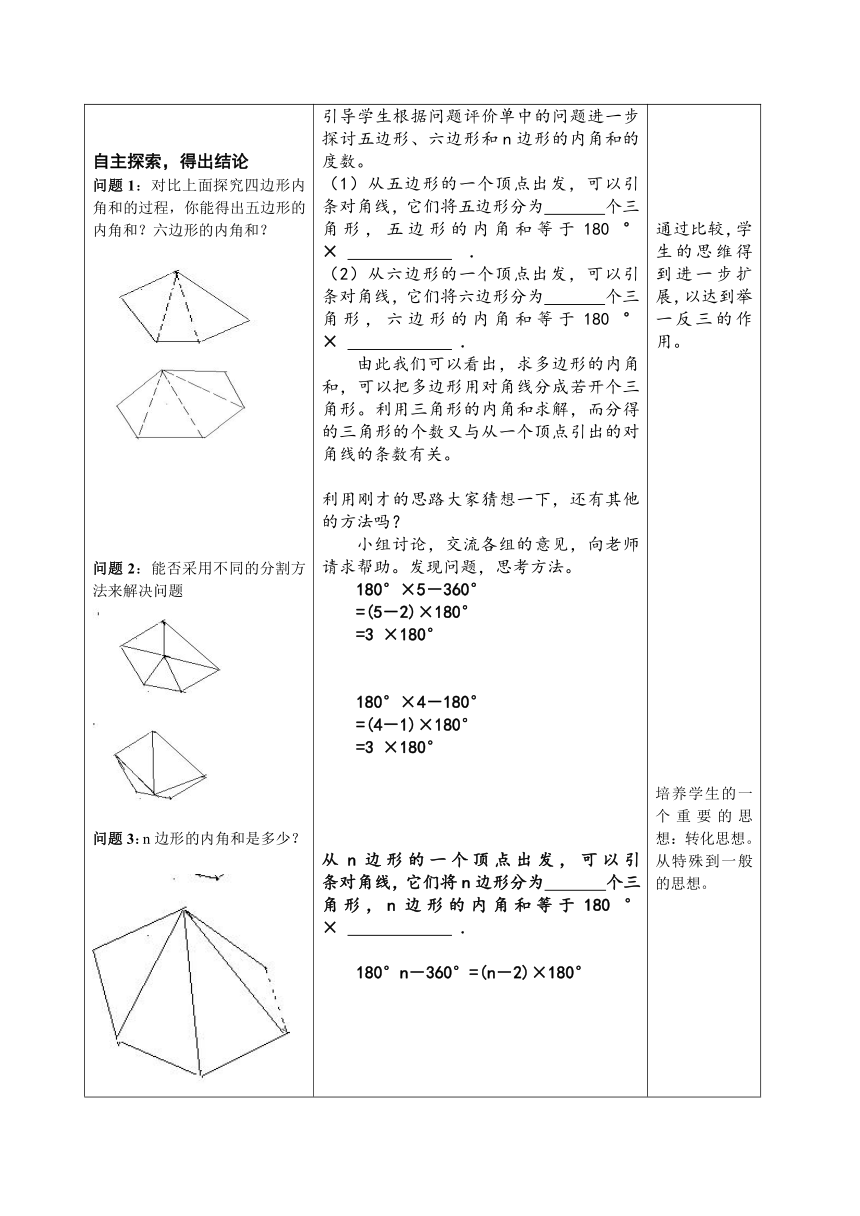
1、对比上面探究四边形内角和的过程,你能得出五边形的内角和?六边形的内角和?
2、能否采用不同的分割方法来解决问题
3、n边形的内角和是多少?
从n边形的一个顶点出发,可以引 条对角线,它们将n边形分为 个三角形,n边形的内角和等于180 °× .
小组评价: 教师评价:
《多边形内角和问题训练——评价单》
设计者: 班级: 姓名:
我要飞得更高
牛刀小试
1、七边形的内角和是( )
A.360° B.720° C.900° D.1260°
2、若一个正多边形的每一个内角都等于120°,则它是( )
A.正八边形 B.正六边形 C.正五边形 D.正方形
3、四边形ABCD中,∠A,∠B,∠C,∠D的度数比为2:3:4:3,则∠D=( )
A.60° B.75° C.90° D.120°
4、如图所示,将多边形分割成三角形、图(1)中可分割出2个三角形;图(2)中可分割出3个三角形;图(3)中可分割出4个三角形;由此你能猜测出,n边形可以分割出( )
个三角形.
能力拓展
5、下图是由10把相同的折扇组成的“蝶恋花”(图1)和梅花图案(图2)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为( )
A.36° B.42° C.45° D.48°
《多边形内角和问题导读——评价单》答案
分析:根据多边形的内角和公式即可得出结果.
解答:解:四边形的内角和=(4-2) 180°=360°.
故选B.
点评:本题主要考查了多边形的内角和定理:n边形的内角和为(n-2) 180°.
分析:根据内角和定理180° (n-2)即可求得.
解答:解:∵多边形的内角和公式为(n-2) 180°,
∴(n-2)×180°=720°,
解得n=6,
∴这个多边形的边数是6.故选C.
点评:本题主要考查了多边形的内角和定理即180° (n-2),难度适中.
3、分析:因为五边形的内角和是(5-2)180°=540度,∠A=100°,则其它各角的度数的和是440°.其余四个内角度数相等,则每个角是440÷4=110度.
解答:解:(5-2)180°=540°,
(540-100)÷4=110°.故选D.
点评:本题主要考查了多边形的内角和定理.
分析:多边形的内角和可以表示成(n-2) 180°(n≥3且n是整数),则多边形的内角
和是180度的度数,由此即可求出答案.
解答:解:因为在这四个选项中不是180°的倍数的只有第二个680°.故选B.
点评:本题主要考查了多边形的内角和定理,是需要识记的内容.
《多边形内角和问题训练——评价单》答案
牛刀小试
1、分析:利用多边形的内角和公式即可解决问题.
解答:解:根据多边形的内角和公式可得:(7-2) 180°=900°.故选C.
点评:本题比较容易,考查了多边形的内角
2、分析:利用多边形内角和公式,根据性质列出方程即可.
解答:解:设此多边形变数为x,根据题意,得
(x-2)×180=120 x,解之,得x=6,所以此图形是正六边形.故选B.
点评:掌握好多边形内角和公式:(n-2)×180.
分析:先设∠A=2X,则∠B=3X,∠C=4X,∠D=3X,再根据四边形的内角和为360°
列方程求解未知数,则可得∠D的值.
解答:解:设∠A=2X,则∠B=3X,∠=4X,∠D=3X,根据四边形的内角和为360°,得∠A+∠B+∠C+∠D=360°,即2X+3X+4X+3X=360°,∴X=30°∠D=3X=90°.故选C.
点评:本题通过设适当的参数,根据四边形的内角和为360°建立方程,求出X的值后再求∠D的值.
4、.分析:(1)三角形分割成了两个三角形;
(2)四边形分割成了三个三角形;
(3)以此类推,n边形分割成了(n-1)个三角形.
解答:解:n边形可以分割出(n-1)个三角形.
点评:此题注意观察:是连接n边形的其中一边上的点.根据具体数值进行分析找规律.n边形分割成了(n-1)个三角形.
能力拓展
5、分析:连接A、B、C、D、E,组成正五边形,求出正五边形的内角度数,减去五角星两旁锐角度数即可得五个锐角的度数.
解答:解:连接图内五点成正五边形内角度数为=108°,∵扇形中心角度为120°∴另外两个角α、β度数是=30°,
∴剩下顶角为108°-2×30°=48°.故选D.
点评:此题考查了等腰三角形的性质和正五边形的性质,将原题转化为正五边形的内角减去相邻两个锐角的度数即可.
【教材分析】
本章及本节的地位与作用是本节课“多边形的内角和”作为本章的一个重点,是三角形有关知识的拓展,学习四边形的基础, 公式的运用还充分地体现了图形与客观世界的密切联系。本节课作为第七章第三节,起着承上启下的作用。在内容上,从三角形内角和到多边形内角和,环环相扣,层层递进,这样编排易于激发学生的学习兴趣,很适合学生的认知特点。通过这节课的学习,可以培养学习探索与归纳能力,体会到从简单到复杂,从特殊到一般和转化等重要的思想方法。
【教学目标】
根据新课程标准的要求,课改应体现学生身心发展特点;应有利于引导学生主动探索和发现;有利于进行创造性的教学。因此,我把本节课的教学目标确定为以下三个方面:
知识目标:
①理解多边形内角和公式的推导过程;
②掌握多边形内角和公式的内涵及其运用。
能力目标:
① 培养学生类比归纳、转化的能力;
②培养学生观察分析、猜想和概括的能力。
思想情感目标:
通过体会数学图形的美感,提高审美能力, 树立认识数学来源于生活,又服务于实践的观点。
【重点与难点】
多边形内角和的公式及公式的推导和运用是本节课的重点;
难点是如何引导学生通过自主学习, 探索多边形内角和的公式。
【学生分析】
初中生作为过程的主体,需要通过积极主动的学习,获取丰富的知识技能和行为经验完成学习过程。初中生的一般特征有初中生的年龄、性别、心理发展水平、学习动机、人格因素、生活经验以及社会背景等方面。
【教学方法】
课前布置学生进行预习,根据自己的学习,完成《问题导读评价单》,从而发现本节课存在的难点问题
课上树立以学生为本的思想,通过创设问题情境,利用《问题生成评价单》,启发引导学生观察----分析----猜想----概括,培养学生积极思考,勇于探索的精神,充分发挥其自主能动性。
最后通过问题训练评价单对学生本节课所学的知识点进行验证,做到查漏补缺
【设计理念】
培养学生学习能力的是教学中的关键,所以在教学中注重针对学生的认知规律,指导他们动手操作、交流合作,是学生独立的去发现问题、探索问题和解决问题。
【教师准备】
《问题导读---评价单》、《问题生成---评价单》、《问题训练---评价单》
【教学过程的设计】
问题与情境 师生活动 设计意图
创设情景,引入新课 三角形的内角和等于180°,正方形,长方形的内角和都等于360°,而其他的四边形的内角和是否也等于360度呢?你能利用三角形内角和定理证明四边形的内角和等于360度 吗?合作交流,探索新知1、动手试一试任意画一个四边形,量出它的四个内角,计算它的内角和。并在小组内交流,猜想四边形的内角和。 能否根据已经学过的三角形内角和知识来解决四边形的内角和?然后在小组内交流,找出简单的方法。2、若任意给出一个多边形,如二十边形,要求它的内角和,如果采用上述的度量法,就得量出二十个内角的度数,再计算。这样很麻烦。所以请同学们思考这样一个问题:能不能利用学过的三角形的内角和来解决这个问题?自主探索,得出结论 问题1:对比上面探究四边形内角和的过程,你能得出五边形的内角和?六边形的内角和?问题2:能否采用不同的分割方法来解决问题问题3:n边形的内角和是多少? 轻松过关发放《问题训练评价单》,让学生独立完成其练习题归纳总结,形成体系 1、归纳本节课学习了以下主要内容:(1)探索了n边形的内角和公式(2)学会转化思想 上课之前先检查学生对《问题导读评价单》的完成情况教师给出问题,带领学生进入到思考的情境中.让学生亲身体验数学发现的过程。在教师的引导下得出结论。深入各组,倾听他们的意见。提问个别学生答案。任意画一个四边形四个内角和为360度。如图,画出任意一个四边形的一条对角线,都能将这个四边形分为两个三角形。所以四边形的内角和为360度。发放《问题生成评价单》,然后小组根据其提出的问题进行讨论,交流各组的意见,向老师请求帮助。发现问题的思考方法。引导学生根据问题评价单中的问题进一步探讨五边形、六边形和n边形的内角和的度数。(1)从五边形的一个顶点出发,可以引 条对角线,它们将五边形分为 个三角形,五边形的内角和等于180 °× .(2)从六边形的一个顶点出发,可以引 条对角线,它们将六边形分为 个三角形,六边形的内角和等于180 °× .由此我们可以看出,求多边形的内角和,可以把多边形用对角线分成若开个三角形。利用三角形的内角和求解,而分得的三角形的个数又与从一个顶点引出的对角线的条数有关。利用刚才的思路大家猜想一下,还有其他的方法吗?小组讨论,交流各组的意见,向老师请求帮助。发现问题,思考方法。180°×5-360° =(5-2)×180°=3 ×180°180°×4-180°=(4-1)×180°=3 ×180°从n边形的一个顶点出发,可以引 条对角线,它们将n边形分为 个三角形,n边形的内角和等于180 °× .180°n-360°=(n-2)×180°教师根据学生的回答,给予评价,并在此过程中规范学生的言语表达。训练学生的逻辑表达能力。学生通过比较,订正自己的错误的过程。提问,引导学生进一步巩固对这一节的认识。学生总结不完整,在教师的指导下完成。 依据新课程的理念,从原有的知识下手,提出问题,引出学生思考。通过学生自己动手,让他们积极参加数学活动,主动思考,合作交流。经过交流,教师向学生提供必要的帮助。体现教师是学生学习的,组织者、合作者、参与者。在得出任意四边形的内角和的求法后,再让学生思考五边形、六边形的内角和的求法,旨在让学生能从中找到规律,为后面求N边形的内角和打下基础通过比较,学生的思维得到进一步扩展,以达到举一反三的作用。培养学生的一个重要的思想:转化思想。从特殊到一般的思想。通过练习,学生加深对所学的知识应用。利用多边形的内角和解答,为这一章节的重难点在练习中起到一个突破的作用。让学生在课堂上有时间进行思考,把时间给学生,体现课堂上学生是教学的主体
《多边形内角和问题导读——评价单》
设计者: 班级: 姓名:
教学目标
知识目标:
①理解多边形内角和公式的推导过程;
②掌握多边形内角和公式的内涵及其运用。
能力目标:
① 培养学生类比归纳、转化的能力;
②培养学生观察分析、猜想和概括的能力。
思想情感目标:
通过体会数学图形的美感,提高审美能力, 树立认识数学来源于生活,又服务于实践的观点。
重点与难点
多边形内角和的公式及公式的推导和运用是本节课的重点;
难点是如何引导学生通过自主学习, 探索多边形内角和的公式。
为你导航
1、四边形的内角和为( )
A.180° B.360° C.540° D.720°
2、一个多边形的内角和是720°,这个多边形的边数是( )
A.4 B.5 C.6 D.7
3、在五边形ABCDE中,若∠A=100°,且其余四个内角度数相等,则∠C=( )
A.65° B.100° C.108° D.110°
4、多边形的内角和不可能为( )
A.180° B.680° C.1080° D.1980°
通过预习本节内容你未解决的问题有:
.
自我评价: 小组评价: 教师评价:
《多边形内角和问题生成——评价单》
设计者: 班级: 姓名:
请同学们在预习的基础上,将生成的问题充分交流后,在单位时间内完成下列题目,并准备多元化展示.
带着问题走进丰富多彩的数学世界
问题一:
1、任意画一个四边形,量出它的四个内角,计算它的内角和。并在小组内交流,猜想四边形的内角和。
2、若任意给出一个多边形,如二十边形,要求它的内角和,如果采用上述的度量法,就得量出二十个内角的度数,再计算。这样很麻烦。所以请同学们思考这样一个问题:能不能利用学过的三角形的内角和来解决这个问题?
问题二:
1、对比上面探究四边形内角和的过程,你能得出五边形的内角和?六边形的内角和?
2、能否采用不同的分割方法来解决问题
3、n边形的内角和是多少?
从n边形的一个顶点出发,可以引 条对角线,它们将n边形分为 个三角形,n边形的内角和等于180 °× .
小组评价: 教师评价:
《多边形内角和问题训练——评价单》
设计者: 班级: 姓名:
我要飞得更高
牛刀小试
1、七边形的内角和是( )
A.360° B.720° C.900° D.1260°
2、若一个正多边形的每一个内角都等于120°,则它是( )
A.正八边形 B.正六边形 C.正五边形 D.正方形
3、四边形ABCD中,∠A,∠B,∠C,∠D的度数比为2:3:4:3,则∠D=( )
A.60° B.75° C.90° D.120°
4、如图所示,将多边形分割成三角形、图(1)中可分割出2个三角形;图(2)中可分割出3个三角形;图(3)中可分割出4个三角形;由此你能猜测出,n边形可以分割出( )
个三角形.
能力拓展
5、下图是由10把相同的折扇组成的“蝶恋花”(图1)和梅花图案(图2)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为( )
A.36° B.42° C.45° D.48°
《多边形内角和问题导读——评价单》答案
分析:根据多边形的内角和公式即可得出结果.
解答:解:四边形的内角和=(4-2) 180°=360°.
故选B.
点评:本题主要考查了多边形的内角和定理:n边形的内角和为(n-2) 180°.
分析:根据内角和定理180° (n-2)即可求得.
解答:解:∵多边形的内角和公式为(n-2) 180°,
∴(n-2)×180°=720°,
解得n=6,
∴这个多边形的边数是6.故选C.
点评:本题主要考查了多边形的内角和定理即180° (n-2),难度适中.
3、分析:因为五边形的内角和是(5-2)180°=540度,∠A=100°,则其它各角的度数的和是440°.其余四个内角度数相等,则每个角是440÷4=110度.
解答:解:(5-2)180°=540°,
(540-100)÷4=110°.故选D.
点评:本题主要考查了多边形的内角和定理.
分析:多边形的内角和可以表示成(n-2) 180°(n≥3且n是整数),则多边形的内角
和是180度的度数,由此即可求出答案.
解答:解:因为在这四个选项中不是180°的倍数的只有第二个680°.故选B.
点评:本题主要考查了多边形的内角和定理,是需要识记的内容.
《多边形内角和问题训练——评价单》答案
牛刀小试
1、分析:利用多边形的内角和公式即可解决问题.
解答:解:根据多边形的内角和公式可得:(7-2) 180°=900°.故选C.
点评:本题比较容易,考查了多边形的内角
2、分析:利用多边形内角和公式,根据性质列出方程即可.
解答:解:设此多边形变数为x,根据题意,得
(x-2)×180=120 x,解之,得x=6,所以此图形是正六边形.故选B.
点评:掌握好多边形内角和公式:(n-2)×180.
分析:先设∠A=2X,则∠B=3X,∠C=4X,∠D=3X,再根据四边形的内角和为360°
列方程求解未知数,则可得∠D的值.
解答:解:设∠A=2X,则∠B=3X,∠=4X,∠D=3X,根据四边形的内角和为360°,得∠A+∠B+∠C+∠D=360°,即2X+3X+4X+3X=360°,∴X=30°∠D=3X=90°.故选C.
点评:本题通过设适当的参数,根据四边形的内角和为360°建立方程,求出X的值后再求∠D的值.
4、.分析:(1)三角形分割成了两个三角形;
(2)四边形分割成了三个三角形;
(3)以此类推,n边形分割成了(n-1)个三角形.
解答:解:n边形可以分割出(n-1)个三角形.
点评:此题注意观察:是连接n边形的其中一边上的点.根据具体数值进行分析找规律.n边形分割成了(n-1)个三角形.
能力拓展
5、分析:连接A、B、C、D、E,组成正五边形,求出正五边形的内角度数,减去五角星两旁锐角度数即可得五个锐角的度数.
解答:解:连接图内五点成正五边形内角度数为=108°,∵扇形中心角度为120°∴另外两个角α、β度数是=30°,
∴剩下顶角为108°-2×30°=48°.故选D.
点评:此题考查了等腰三角形的性质和正五边形的性质,将原题转化为正五边形的内角减去相邻两个锐角的度数即可.
