3.1.2椭圆的几何性质(第一课时)课件(共17张PPT)——2020-2021学年高二上学期数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 3.1.2椭圆的几何性质(第一课时)课件(共17张PPT)——2020-2021学年高二上学期数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 00:00:00 | ||
图片预览



文档简介
3.1.2椭圆的几何性质
第一课时
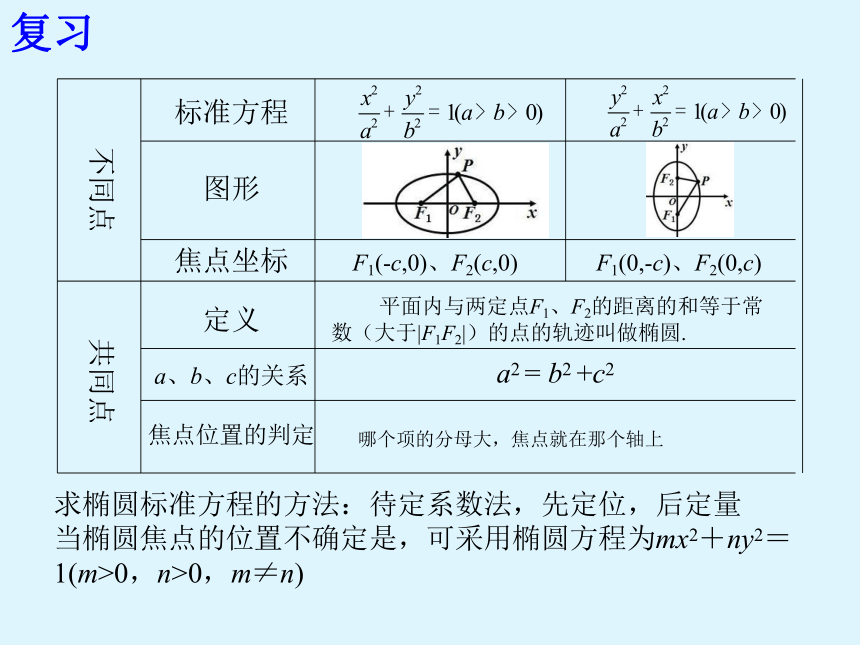
标准方程
图形
焦点坐标
定义
a、b、c的关系
焦点位置的判定
共同点
不同点
F1(-c,0)、F2(c,0)
F1(0,-c)、F2(0,c)
平面内与两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
a2 = b2 +c2
哪个项的分母大,焦点就在那个轴上
复习
求椭圆标准方程的方法:待定系数法,先定位,后定量
当椭圆焦点的位置不确定是,可采用椭圆方程为mx2+ny2=1(m>0,n>0,m≠n)
o
y
B2
B1
A1
A2
F1
F2
c
a
b
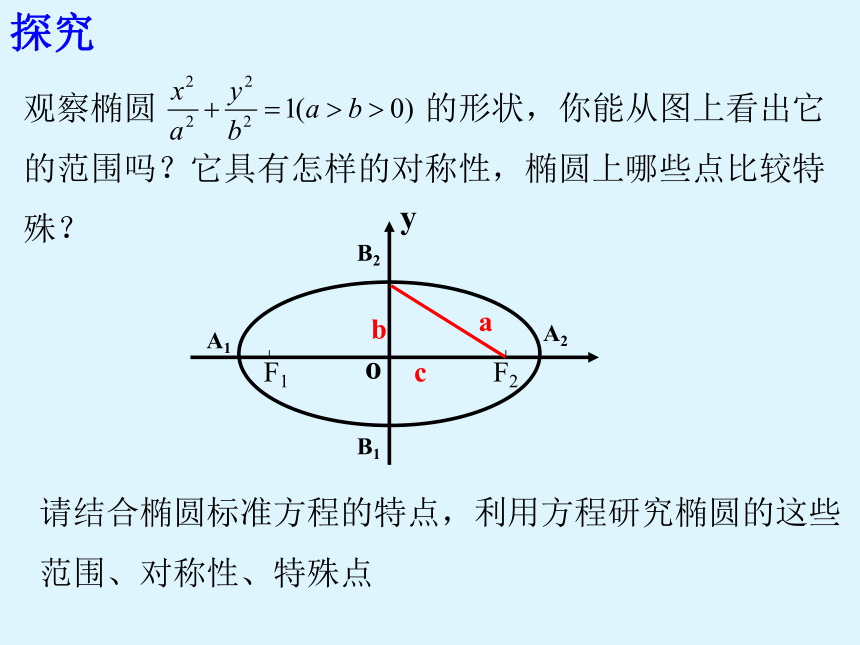
观察椭圆 的形状,你能从图上看出它的范围吗?它具有怎样的对称性,椭圆上哪些点比较特殊?
探究
请结合椭圆标准方程的特点,利用方程研究椭圆的这些范围、对称性、特殊点
1.范围
说明:椭圆落在x =±a,y =±b围成的矩形中
o
y
B2
B1
A1
A2
F1
F2
c
a
b
x
新知
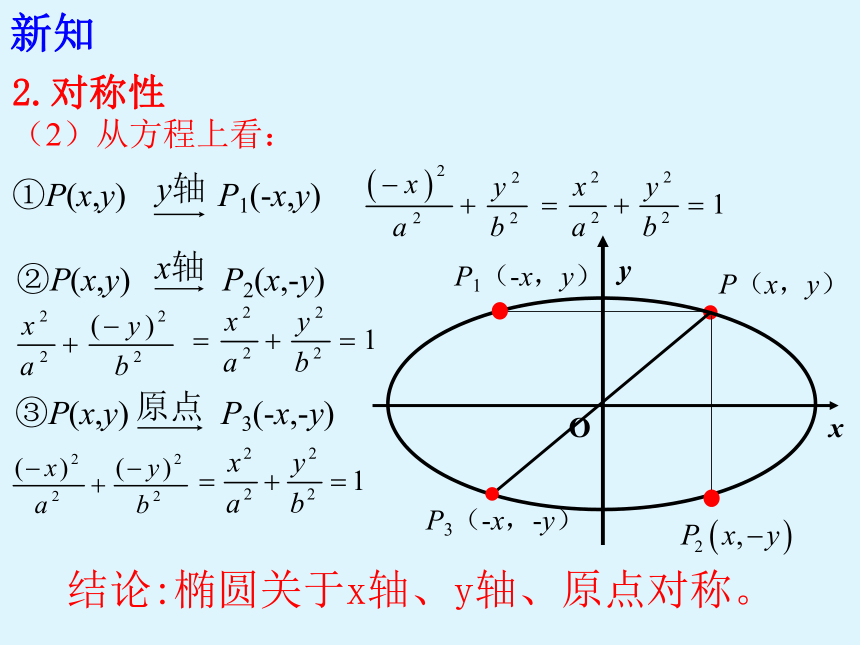
2.对称性
y
x
O
P(x,y)
P1(-x,y)
P3(-x,-y)
从图形上看:椭圆关于x轴、y轴的轴对称图形,又是中心对称图形;坐标原点为对称中心(椭圆的中心)
新知
(2)从方程上看:
①P(x,y) P1(x1,y1)
2.对称性
新知
(2)从方程上看:
①P(x,y) P1(-x,y)
②P(x,y) P2(x,-y)
③P(x,y) P3(-x,-y)
结论:椭圆关于x轴、y轴、原点对称。
y
x
O
P(x,y)
P1(-x,y)
P3(-x,-y)
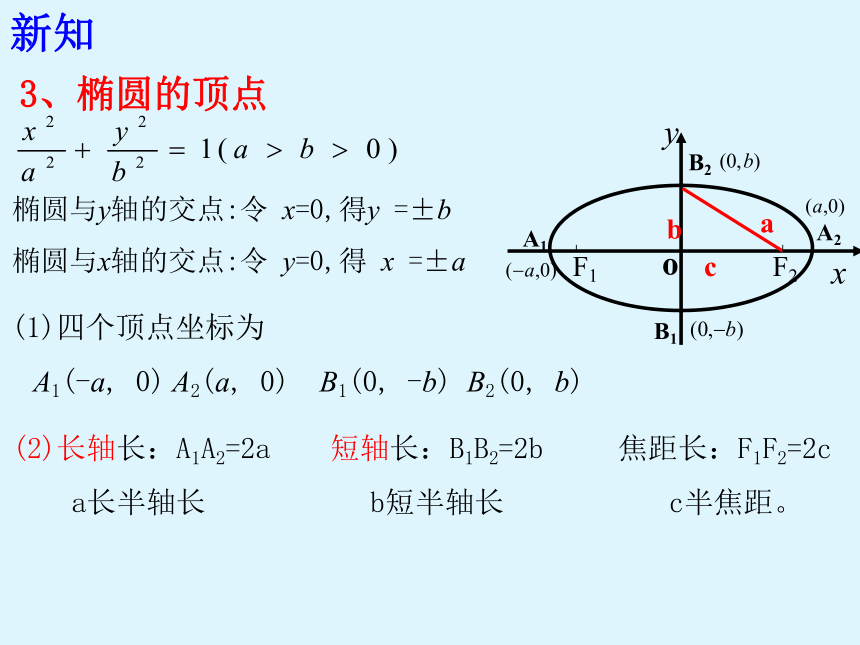
3、椭圆的顶点
椭圆与y轴的交点:令 x=0,得y =±b
椭圆与x轴的交点:令 y=0,得 x =±a
o
y
B2
B1
A1
A2
F1
F2
c
a
b
(1)四个顶点坐标为
A1(-a, 0) A2(a, 0) B1(0, -b) B2(0, b)
x
新知
(2)长轴长:A1A2=2a 短轴长:B1B2=2b 焦距长:F1F2=2c
a长半轴长 b短半轴长 c半焦距。
1
2
3
-1
-2
-3
-4
4
y
1
2
3
-1
-2
-3
-4
4
y
1
2
3
4
5
-1
-5
-2
-3
-4
x
1
2
3
4
5
-1
-5
-2
-3
-4
x
根据前面所学有关知识画出下列图形
(1)
(2)
A1
B1
A2
B2
B2
A2
B1
A1
练习
x
y
x
4.离心率
椭圆的焦距与长轴长的比叫做椭圆的离心率。
刻画椭圆的扁圆程度:
离心率
思考
1.椭圆的离心率在什么范围内?
2.椭圆的离心率在范围内变化时椭圆形状如何变化?
新知
离心率的取值范围
因为 a > c > 0,所以0e 越大越扁
e 越接近1,椭圆就越扁
e 越接近 0,椭圆就越圆
③特例:e =0,椭圆变为圆,方程变为
例4.求椭圆16x2+25y2=400的长轴和短轴的长、离心率、焦点和顶点的坐标
解:把原方程化为标准方程得
于是a=5,b=4,c=3
因此长轴长为10;短轴长为8;焦距为6;
离心率为 ;
焦点坐标为(3,0)、(-3,0),
顶点坐标为(5,0)、(-5,0)、(0,4)、(0,-4);
例题
已知椭圆方程为6x2+y2=6
它的长轴长是: 。短轴长是: 。
焦距是: .离心率等于: 。
焦点坐标是: 顶点坐标是: 。
外切矩形的面积等于: 。
2
练习
用标准方程研究几何性质的步骤
(1)将椭圆方程化为标准形式.
(2)确定焦点位置.
(3)求出a,b,c.
(4)写出椭圆的几何性质.
归纳
求适合下列条件的椭圆的标准方程
(1) 焦点在y轴上,c = 3 ,e=
(2)经过P(-3,0),Q(0,-2)两点
(3)长轴长等于20,离心率等于
(4)长轴长是短轴长的2倍,且经过点P(3,0)
练习
(4)长轴长是短轴长的2倍,且经过点P(3,0)
练习
解:①当焦点在x轴上时,a=3
则6=2×2b 所以b=
所以椭圆的标准方程为
②当焦点在y轴上时,b=3
则2a=12 所以a=6
所以椭圆的标准方程为
故椭圆的标准方程为
根据椭圆的几何性质求标准方程
此类问题通常采用待定系数法,
其步骤仍然是“先定型,后计算”,
即首先确定焦点位置,
其次根据已知条件构造关于参数的关系式,
利用方程(组)求得参数.
归纳
标准方程
图象
范围
对称性
顶点坐标
焦点坐标
半轴长
焦距
a,b,c关系
离心率
|x|≤ a,|y|≤ b
|x|≤ b,|y|≤ a
关于x轴、y轴成轴对称;关于原点成中心对称
长半轴长为a,短半轴长为b.
焦距为2c;
a2=b2+c2
(a,0)、(-a,0)、(0,b)、(0,-b)
(b,0)、(-b,0)、(0,a)、(0,-a)
(c,0)、(-c,0)
(0 , c)、(0, -c)
(0小结
作业
课本P112练习 3、4
第一课时
标准方程
图形
焦点坐标
定义
a、b、c的关系
焦点位置的判定
共同点
不同点
F1(-c,0)、F2(c,0)
F1(0,-c)、F2(0,c)
平面内与两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
a2 = b2 +c2
哪个项的分母大,焦点就在那个轴上
复习
求椭圆标准方程的方法:待定系数法,先定位,后定量
当椭圆焦点的位置不确定是,可采用椭圆方程为mx2+ny2=1(m>0,n>0,m≠n)
o
y
B2
B1
A1
A2
F1
F2
c
a
b
观察椭圆 的形状,你能从图上看出它的范围吗?它具有怎样的对称性,椭圆上哪些点比较特殊?
探究
请结合椭圆标准方程的特点,利用方程研究椭圆的这些范围、对称性、特殊点
1.范围
说明:椭圆落在x =±a,y =±b围成的矩形中
o
y
B2
B1
A1
A2
F1
F2
c
a
b
x
新知
2.对称性
y
x
O
P(x,y)
P1(-x,y)
P3(-x,-y)
从图形上看:椭圆关于x轴、y轴的轴对称图形,又是中心对称图形;坐标原点为对称中心(椭圆的中心)
新知
(2)从方程上看:
①P(x,y) P1(x1,y1)
2.对称性
新知
(2)从方程上看:
①P(x,y) P1(-x,y)
②P(x,y) P2(x,-y)
③P(x,y) P3(-x,-y)
结论:椭圆关于x轴、y轴、原点对称。
y
x
O
P(x,y)
P1(-x,y)
P3(-x,-y)
3、椭圆的顶点
椭圆与y轴的交点:令 x=0,得y =±b
椭圆与x轴的交点:令 y=0,得 x =±a
o
y
B2
B1
A1
A2
F1
F2
c
a
b
(1)四个顶点坐标为
A1(-a, 0) A2(a, 0) B1(0, -b) B2(0, b)
x
新知
(2)长轴长:A1A2=2a 短轴长:B1B2=2b 焦距长:F1F2=2c
a长半轴长 b短半轴长 c半焦距。
1
2
3
-1
-2
-3
-4
4
y
1
2
3
-1
-2
-3
-4
4
y
1
2
3
4
5
-1
-5
-2
-3
-4
x
1
2
3
4
5
-1
-5
-2
-3
-4
x
根据前面所学有关知识画出下列图形
(1)
(2)
A1
B1
A2
B2
B2
A2
B1
A1
练习
x
y
x
4.离心率
椭圆的焦距与长轴长的比叫做椭圆的离心率。
刻画椭圆的扁圆程度:
离心率
思考
1.椭圆的离心率在什么范围内?
2.椭圆的离心率在范围内变化时椭圆形状如何变化?
新知
离心率的取值范围
因为 a > c > 0,所以0
e 越接近1,椭圆就越扁
e 越接近 0,椭圆就越圆
③特例:e =0,椭圆变为圆,方程变为
例4.求椭圆16x2+25y2=400的长轴和短轴的长、离心率、焦点和顶点的坐标
解:把原方程化为标准方程得
于是a=5,b=4,c=3
因此长轴长为10;短轴长为8;焦距为6;
离心率为 ;
焦点坐标为(3,0)、(-3,0),
顶点坐标为(5,0)、(-5,0)、(0,4)、(0,-4);
例题
已知椭圆方程为6x2+y2=6
它的长轴长是: 。短轴长是: 。
焦距是: .离心率等于: 。
焦点坐标是: 顶点坐标是: 。
外切矩形的面积等于: 。
2
练习
用标准方程研究几何性质的步骤
(1)将椭圆方程化为标准形式.
(2)确定焦点位置.
(3)求出a,b,c.
(4)写出椭圆的几何性质.
归纳
求适合下列条件的椭圆的标准方程
(1) 焦点在y轴上,c = 3 ,e=
(2)经过P(-3,0),Q(0,-2)两点
(3)长轴长等于20,离心率等于
(4)长轴长是短轴长的2倍,且经过点P(3,0)
练习
(4)长轴长是短轴长的2倍,且经过点P(3,0)
练习
解:①当焦点在x轴上时,a=3
则6=2×2b 所以b=
所以椭圆的标准方程为
②当焦点在y轴上时,b=3
则2a=12 所以a=6
所以椭圆的标准方程为
故椭圆的标准方程为
根据椭圆的几何性质求标准方程
此类问题通常采用待定系数法,
其步骤仍然是“先定型,后计算”,
即首先确定焦点位置,
其次根据已知条件构造关于参数的关系式,
利用方程(组)求得参数.
归纳
标准方程
图象
范围
对称性
顶点坐标
焦点坐标
半轴长
焦距
a,b,c关系
离心率
|x|≤ a,|y|≤ b
|x|≤ b,|y|≤ a
关于x轴、y轴成轴对称;关于原点成中心对称
长半轴长为a,短半轴长为b.
焦距为2c;
a2=b2+c2
(a,0)、(-a,0)、(0,b)、(0,-b)
(b,0)、(-b,0)、(0,a)、(0,-a)
(c,0)、(-c,0)
(0 , c)、(0, -c)
(0
作业
课本P112练习 3、4
