3.3 幂函数教学课件(共32张PPT)——2021-2022学年高一上学期数学人教 A版 (2019)必修第一册
文档属性
| 名称 | 3.3 幂函数教学课件(共32张PPT)——2021-2022学年高一上学期数学人教 A版 (2019)必修第一册 |  | |
| 格式 | zip | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 12:25:57 | ||
图片预览







文档简介
(共32张PPT)
3.3
幂函数
主讲人:
1、掌握幂函数的概念。
熟悉
时,幂函数 的
图像和性质。
2、能利用幂函数的性质来解决一些实际问题
,例如比较大小
3、通过对情景的观察、思考、归纳、总结形成结论,培养发现问题、解决
问题的能力。
从五个具体幂函数中认识幂函数的一些性质
重点
难点
画五个幂函数的图象并由图象概括其性质
学习目标
问题1:
如果热烧饼售价为
1
元一张,购买
x
张,需要支付的钱数y=?
问题2:如果一个正方形的烧饼仓库边长为x,那么仓库的面积y=?
问题3:如果正方体的烧饼包装盒棱长为x,那么包装盒的体积y=?
问题4:如果正方形烧饼仓库的面积为x,那么仓库的边长y=?
问题5:
如果小明去买烧饼,x
秒内骑车行进
1千米,那么他骑车的平均速度y=?
创设情境,导入课题
周村烧饼闻名天下,请同学们阅读回答问题。
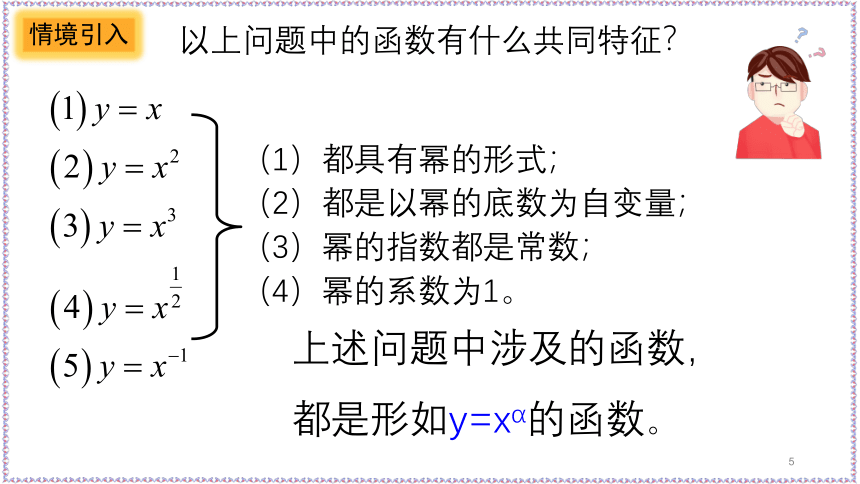
以上问题中的函数有什么共同特征?
(1)都具有幂的形式;
(2)都是以幂的底数为自变量;
(3)幂的指数都是常数;
(4)幂的系数为1。
上述问题中涉及的函数,
都是形如y=xα的函数。
情境引入
5
一般地,函数 叫做幂函数(power
function)
,
几点说明:
幂函数定义
判断下列函数是否为幂函数.
(1)
y=x4
(3)
y=
-xe
(5)
y=2x2
(6)
y=x3+2
判一判
1
2
-1
-2
1
2
-1
-2
-1
1
2
3
1
-1
x
y
x
y
1
2
-2
-1
-1
2
1
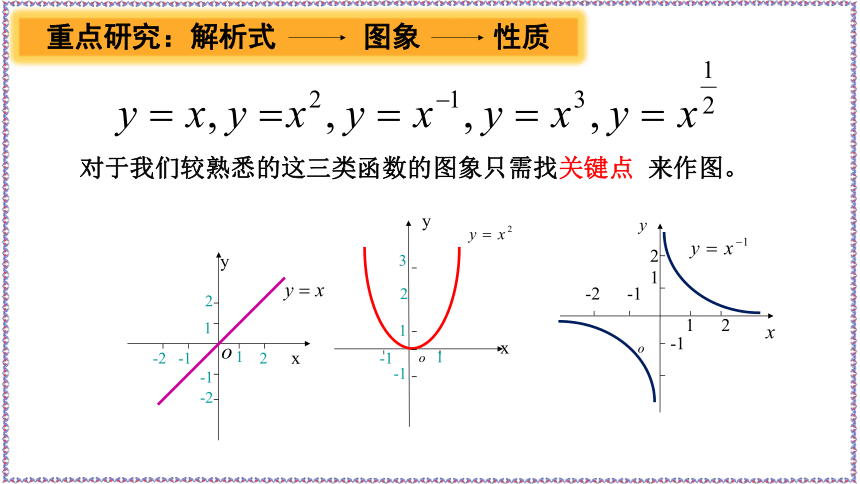
对于我们较熟悉的这三类函数的图象只需找关键点
来作图。
重点研究:解析式
图象
性质
o
1
2
-1
-2
1
o
1
1
-1
-1
-2
-2
-1
2
3
4
6
1
0
1
2
0
-1
-1
0
1
0
1
描点法作图
1.5
x
y
O
y=x
1
1
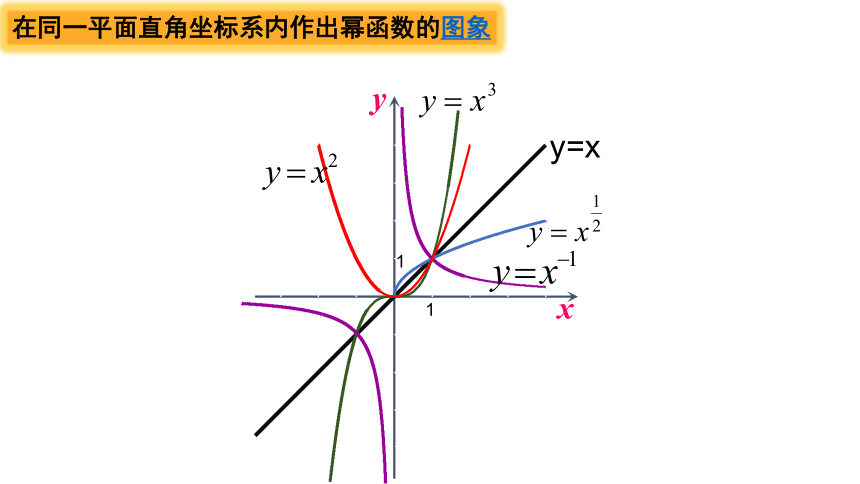
在同一平面直角坐标系内作出幂函数的图象
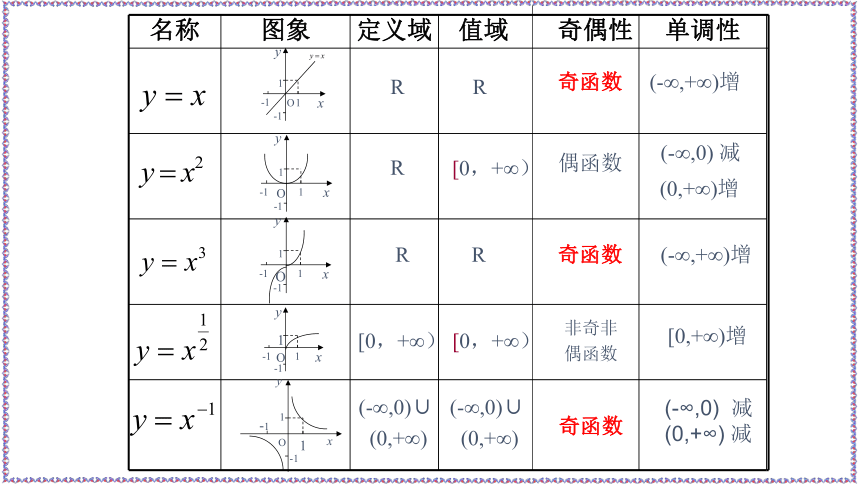
名称
图象
定义域
值域
奇偶性
单调性
O
x
y
1
1
-1
-1
O
x
y
1
1
-1
-1
O
x
y
1
1
-1
-1
O
x
y
1
1
-1
-1
R
R
R
[0,+∞)
奇函数
偶函数
奇函数
非奇非
偶函数
奇函数
(0,+∞)增
(-∞,0)
减
(-∞,+∞)增
(-∞,+∞)增
[0,+∞)增
(-∞,0)
减
(0,+∞)
减
O
x
y
1
1
-1
-1
(-∞,0)∪
(0,+∞)
R
[0,+∞)
[0,+∞)
(-∞,0)∪
(0,+∞)
R
动画演示
在同一平面直角坐标系内作出以下幂函数的图像
x
y
O
y=x
1
1
幂函数图象在第一象限的分布情况:
y
=1
1
1
0
x
13
归纳
合作探究:小组合作讨论
问题
1
:
从图象的位置分布规律上看,它们有什么
特点?
问题
2
:
从公共点上看,
它们有什么特点?
问题
3
:
从奇偶性上看,
它们有什么共同点?
(提示,
当α为整数时)
问题
4
:
单调性上看,
它们有什么共同点?
合作探究:小组合作讨论
问题
1
:
从图象的位置分布规律
上看,它们有什么特点?
回答:图象都过第一象限,图象不过第四象
限,二三象限看奇偶
合作探究:小组合作讨论
问题
2
:
从公共点上看,
它们有什么特点?
回答(1)所有图象都通过点
(1,1)
;
(2)α>0,则图像都过点(0,0)和(1,1)(3)α<0,则图像都过点(1,1)
合作探究:小组合作讨论
问题
3
:
从奇偶性上看,
它们有什么共同点?(提示,
当α为整数时)
回答:当
α为奇数时,幂函数为奇函数;
当α为偶数时,幂函数为偶函数。
合作探究:小组合作讨论
问题
4
:
单调性上看,
它们有什么共同点?
回答:当α>0,在第一象限内递增;
若
α<0,在第一象限内递减且图象向上与y轴无限接近,向右与x轴无限接近。
一象限,图都有;
四象限,都没有;
二和三,看奇偶;
都过1
,正过0;
单调性,正递增,负递减
奇偶性,看指数;指奇奇,指偶偶;
19
三字经:幂函数的图象与性质
例1:判断幂函数
的单调性,并证明.
用定义证明函数的单调性的步骤:
(1).
取值:设x1,
x2是某个区间上任意二值,且x1<x2;
(2).
作差:
f(x1)-f(x2),
(3)
变形
:
(4).
判断
f(x1)-f(x2)
的符号;
(5).
下结论.
例题讲解1
证明:函数的定义域是
[0,+∞),任取x1,x2∈
[0,+∞),且x1<x2,则
注意:若给出的函数是有根号的式子,往往
采用有理化的方式。
.
)
,
0
[
)
(
上是增函数
在
所以幂函数
+?
=
x
x
f
)
(
)
(
,
0
,
0
2
1
2
1
2
1
x
f
x
f
x
x
x
x
<
>
+
<
-
所以
因为
解:由幂函数的定义知b=1
所以f(x)=xα,将
代入,得
总结:
理解并掌握形如y=xα的形式就是幂函数。
例2:已知幂函数
的图象过点
,
试求出此函数的解析式.
例题讲解2
例3:
比较下列各题中两数值的大小
①
1.73,1.83
②
0.8-1
,0.9-1
解:
①
∵幂函数y=x
3
在R上是单调增函数。
又∵1.7<1.8
∴1.73<1.83
又∵0.8<0.9
∴0.8-1
>
0.9-1
例题讲解3
②
∵幂函数y=
x-1在(0,+∞)上是单调减函数.
课堂检测1
课堂检测2
3、如果函数f
(x)
=
(m2-m-1)
xm是幂函数,且在区间(0,+∞)上是减函数,求满足条件的实数m的值。
课堂检测3
课堂检测4
小结
(1)
幂函数的定义;
(2)
幂函数的分布规律;
(3)
幂函数的简单应用:利用单调性判别大小
(4)一个方法:研究函数的一般方法。
两个思想:数形结合的数学思想,由特殊到一般的归纳思想
积跬步以致千里,积怠惰以致深渊
每天比你努力多一点的人,一年后已经甩你很远了
励志数学
“人生在勤,勤则不匮”
幸福不会从天降,美好生活靠劳动创造。
——2016年4月26日,习近平在知识分子、劳动模范、青年代表座谈会上的讲话
平语近人
课本91页习题3.3
课后作业
感谢您的聆听
谢谢大家
3.3
幂函数
主讲人:
1、掌握幂函数的概念。
熟悉
时,幂函数 的
图像和性质。
2、能利用幂函数的性质来解决一些实际问题
,例如比较大小
3、通过对情景的观察、思考、归纳、总结形成结论,培养发现问题、解决
问题的能力。
从五个具体幂函数中认识幂函数的一些性质
重点
难点
画五个幂函数的图象并由图象概括其性质
学习目标
问题1:
如果热烧饼售价为
1
元一张,购买
x
张,需要支付的钱数y=?
问题2:如果一个正方形的烧饼仓库边长为x,那么仓库的面积y=?
问题3:如果正方体的烧饼包装盒棱长为x,那么包装盒的体积y=?
问题4:如果正方形烧饼仓库的面积为x,那么仓库的边长y=?
问题5:
如果小明去买烧饼,x
秒内骑车行进
1千米,那么他骑车的平均速度y=?
创设情境,导入课题
周村烧饼闻名天下,请同学们阅读回答问题。
以上问题中的函数有什么共同特征?
(1)都具有幂的形式;
(2)都是以幂的底数为自变量;
(3)幂的指数都是常数;
(4)幂的系数为1。
上述问题中涉及的函数,
都是形如y=xα的函数。
情境引入
5
一般地,函数 叫做幂函数(power
function)
,
几点说明:
幂函数定义
判断下列函数是否为幂函数.
(1)
y=x4
(3)
y=
-xe
(5)
y=2x2
(6)
y=x3+2
判一判
1
2
-1
-2
1
2
-1
-2
-1
1
2
3
1
-1
x
y
x
y
1
2
-2
-1
-1
2
1
对于我们较熟悉的这三类函数的图象只需找关键点
来作图。
重点研究:解析式
图象
性质
o
1
2
-1
-2
1
o
1
1
-1
-1
-2
-2
-1
2
3
4
6
1
0
1
2
0
-1
-1
0
1
0
1
描点法作图
1.5
x
y
O
y=x
1
1
在同一平面直角坐标系内作出幂函数的图象
名称
图象
定义域
值域
奇偶性
单调性
O
x
y
1
1
-1
-1
O
x
y
1
1
-1
-1
O
x
y
1
1
-1
-1
O
x
y
1
1
-1
-1
R
R
R
[0,+∞)
奇函数
偶函数
奇函数
非奇非
偶函数
奇函数
(0,+∞)增
(-∞,0)
减
(-∞,+∞)增
(-∞,+∞)增
[0,+∞)增
(-∞,0)
减
(0,+∞)
减
O
x
y
1
1
-1
-1
(-∞,0)∪
(0,+∞)
R
[0,+∞)
[0,+∞)
(-∞,0)∪
(0,+∞)
R
动画演示
在同一平面直角坐标系内作出以下幂函数的图像
x
y
O
y=x
1
1
幂函数图象在第一象限的分布情况:
y
=1
1
1
0
x
13
归纳
合作探究:小组合作讨论
问题
1
:
从图象的位置分布规律上看,它们有什么
特点?
问题
2
:
从公共点上看,
它们有什么特点?
问题
3
:
从奇偶性上看,
它们有什么共同点?
(提示,
当α为整数时)
问题
4
:
单调性上看,
它们有什么共同点?
合作探究:小组合作讨论
问题
1
:
从图象的位置分布规律
上看,它们有什么特点?
回答:图象都过第一象限,图象不过第四象
限,二三象限看奇偶
合作探究:小组合作讨论
问题
2
:
从公共点上看,
它们有什么特点?
回答(1)所有图象都通过点
(1,1)
;
(2)α>0,则图像都过点(0,0)和(1,1)(3)α<0,则图像都过点(1,1)
合作探究:小组合作讨论
问题
3
:
从奇偶性上看,
它们有什么共同点?(提示,
当α为整数时)
回答:当
α为奇数时,幂函数为奇函数;
当α为偶数时,幂函数为偶函数。
合作探究:小组合作讨论
问题
4
:
单调性上看,
它们有什么共同点?
回答:当α>0,在第一象限内递增;
若
α<0,在第一象限内递减且图象向上与y轴无限接近,向右与x轴无限接近。
一象限,图都有;
四象限,都没有;
二和三,看奇偶;
都过1
,正过0;
单调性,正递增,负递减
奇偶性,看指数;指奇奇,指偶偶;
19
三字经:幂函数的图象与性质
例1:判断幂函数
的单调性,并证明.
用定义证明函数的单调性的步骤:
(1).
取值:设x1,
x2是某个区间上任意二值,且x1<x2;
(2).
作差:
f(x1)-f(x2),
(3)
变形
:
(4).
判断
f(x1)-f(x2)
的符号;
(5).
下结论.
例题讲解1
证明:函数的定义域是
[0,+∞),任取x1,x2∈
[0,+∞),且x1<x2,则
注意:若给出的函数是有根号的式子,往往
采用有理化的方式。
.
)
,
0
[
)
(
上是增函数
在
所以幂函数
+?
=
x
x
f
)
(
)
(
,
0
,
0
2
1
2
1
2
1
x
f
x
f
x
x
x
x
<
>
+
<
-
所以
因为
解:由幂函数的定义知b=1
所以f(x)=xα,将
代入,得
总结:
理解并掌握形如y=xα的形式就是幂函数。
例2:已知幂函数
的图象过点
,
试求出此函数的解析式.
例题讲解2
例3:
比较下列各题中两数值的大小
①
1.73,1.83
②
0.8-1
,0.9-1
解:
①
∵幂函数y=x
3
在R上是单调增函数。
又∵1.7<1.8
∴1.73<1.83
又∵0.8<0.9
∴0.8-1
>
0.9-1
例题讲解3
②
∵幂函数y=
x-1在(0,+∞)上是单调减函数.
课堂检测1
课堂检测2
3、如果函数f
(x)
=
(m2-m-1)
xm是幂函数,且在区间(0,+∞)上是减函数,求满足条件的实数m的值。
课堂检测3
课堂检测4
小结
(1)
幂函数的定义;
(2)
幂函数的分布规律;
(3)
幂函数的简单应用:利用单调性判别大小
(4)一个方法:研究函数的一般方法。
两个思想:数形结合的数学思想,由特殊到一般的归纳思想
积跬步以致千里,积怠惰以致深渊
每天比你努力多一点的人,一年后已经甩你很远了
励志数学
“人生在勤,勤则不匮”
幸福不会从天降,美好生活靠劳动创造。
——2016年4月26日,习近平在知识分子、劳动模范、青年代表座谈会上的讲话
平语近人
课本91页习题3.3
课后作业
感谢您的聆听
谢谢大家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
