黑龙江省双鸭山市高中2020-2021学年高一下学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 黑龙江省双鸭山市高中2020-2021学年高一下学期期末考试数学试题 Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 574.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 11:31:57 | ||
图片预览



文档简介
双鸭山市高中2020-2021学年度下学期高(一)
数学期末试题
第Ⅰ卷(选择题)
一、单选题(每小题5分,共60分)
1.设false,则false( )
A.false B.false C.false D.false
2.电影《我和我的家乡》于2020年10月11日在中国内地上映,到2020年10月14日已累计票房22.33亿,创造了多个票房记录,某新闻机构想了解全国人民对《我和我的家乡》的评价,决定从某市3个区按人口数用分层抽样的方法抽取一个样本.若3个区人口数之比为false,且人口最多的一个区抽出100人,则这个样本的容量等于( )
A.100 B.160 C.200 D.240
3.一个圆锥的侧面展开图是圆心角为false,弧长为false的扇形,则该圆锥轴截面的面积false( )
A.false B.false C.false D.false
4.在普通高中新课程改革中,某地实施“false”选课方案.该方案中“2”指的是从政治、地理、化学、生物4门中任选2门作为选考科目,假设每门科目被选中的可能性相等,那么化学和生物至多有一门被选中的概率是( )
A.false B.false C.false D.false
5.已知在正四面体false中,点E为棱false的中点,则异面直线false与false成角的余弦值为( )
A.false B.false C.false D.false
6.天气预报说,在今后的三天中,每一天下雨的概率均为40%,用数字0,1,2,3表示下雨,数字4,5,6,7,8,9表示不下雨,由计算机产生如下20组随机数:
977,864,191,925,271,932,812,458,569,683,
431,257,394,027,556,488,730,113,537,908.
由此估计今后三天中至少有一天下雨的概率为( )
A.0.6 B.0.7 C.0.75 D.0.8
7.已知false,则false等于( )
A.false B.97 C.false D.61
8.已知在false中,a,b,c分别为内角A,B,C的对边,false,且false,则false( )
A.6 B.10 C.12 D.16
9.2021年是中国共产党建党100周年,为全面贯彻党的教育方针,提高学生的审美水平和人文素养,促进学生全面发展.某学校高一年级举办了班级合唱活动.现从全校学生中随机抽取部分学生,并邀请他们为此次活动评分(单位:分,满分100分),对评分进行整理,得到如图所示的频率分布直方图,则下列结论不正确的是( )
A.false
B.若该学校有3000名学生参与了评分,则估计评分超过90分的学生人数为600
C.学生评分的众数的估计值为85
D.学生评分的中位数的估计值为83
10.设false的内角A、B、C的对边分别是a,b,c,false,且B为钝角.false的取值范围( )
A.false B.false C.false D.false
11.在三棱锥false中,false,则该三棱锥的外接球的表面积为( )
A.false B.false C.false D.false
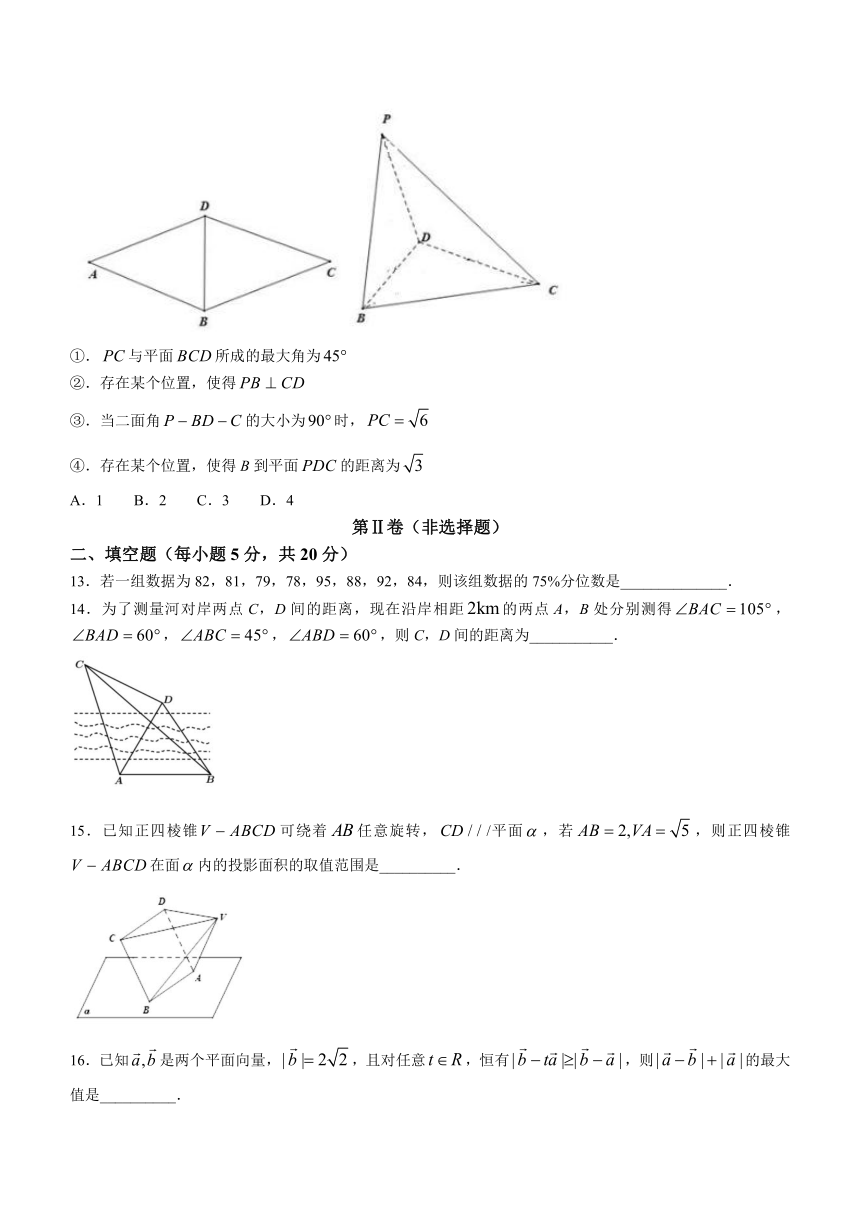
12.如图,在菱形false中,false,将false沿对角线false翻折到false位置,连结false,则在翻折过程中,下列说法正确的( )个
①.false与平面false所成的最大角为false
②.存在某个位置,使得false
③.当二面角false的大小为false时,false
④.存在某个位置,使得B到平面false的距离为false
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题)
二、填空题(每小题5分,共20分)
13.若一组数据为82,81,79,78,95,88,92,84,则该组数据的75%分位数是______________.
14.为了测量河对岸两点C,D间的距离,现在沿岸相距false的两点A,B处分别测得false,false,false,false,则C,D间的距离为___________.
15.已知正四棱锥false可绕着false任意旋转,false/平面false,若false,则正四棱锥false在面false内的投影面积的取值范围是__________.
16.已知false是两个平面向量,false,且对任意false,恒有false,则false的最大值是__________.
三、解答题(第17题10分,18-22题每题12分,共70分)
17.如图,在平行六面体false中,以顶点A为端点的三条棱长度都为2,且两两夹角为false.
(1)求false的长;(2)求false与false所成角的余弦值.
18.A,B两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
A组:10,11,12,13,14,15,16
B组:12,13,15,16,17,14,a
假设所有病人的康复时间互相独立,从A,B两组随机各选1人,A组选出的人记为甲,B组选出的人记为乙.
(1)求甲的康复时间不少于14天的概率;
(2)如果false,求甲的康复时间比乙的康复时间长的概率;
(3)当a为何值时,A,B两组病人康复时间的方差相等?(结论不要求证明,只写出结果)
19.如图,在四棱锥false中,平面false平面false,四边形false为矩形,false,false,M为false的中点.
(1)求证:平面false平面false;
(2)求二面角false的余弦值.
20.已知false的三个内角A,B,C的对边分别为a,b,c且满足false.
(1)求b的值;
(2)若false平分false交false于点D,求false的面积.
21.如图所示的几何体是由三棱柱false和四棱锥false组合而成的,已知false,线段false与false交于点E,E,F分别为线段false的中点,平面false平面false平面false.
(1)求证:四边形false为平行四边形;
(2)若false是边长为2的等边三角形,false,求直线false与平面false所成角的正弦值.
22.某医学科研单位有甲,乙两个专门从事病毒治愈的研发小组,为了比较他们的研发水平,现随机抽取了这两个小组在过去一年里其中经过15次各自研发的新药结果如下:falsefalse其中false分别表示甲组研发新药成功和失败;false分别表示乙组研发新药成功与失败.(1)根据上面这组数据,计算恰有一组研发新药成功的条件下,甲,乙两组同时都研发新药成功的概率.(2)若某组成功研发一种新药,则该组可直接为本单位创造经济价值为5万余元,并且单位奖励给该组1千元,否则就亏损1万余元,奖励0元,试计算甲,乙两组研发新药的经济效益的平均数;
(3)根据(2)的条件分别计算甲乙两组的奖金的方差,并且比较甲乙两组的研发水平;
高一期末数学答案
一、选择题:本题共12小题,每小题5分,共60分.
CCBDAB CBDAAB
二、填空题(每题5分,共20分)
13.90 14.2 15.false 16.4
三、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤
17.(1)false;(2)false
18.【答案】(1)false,(2)false,(3)false或18
【解析】
试题分析:针对甲有7种情况,康复时间不少于14天有3种情况,概率为false;如果false,甲、乙随机各取一人有49种情况,用列举法列出甲的康复时间比乙的康复时间长的情况有10种,概率为false,由于A组数据为10,11,12,13,14,15,16;B组数据调整为a,12,13,14,15,16,17,或12,13,14,15,16,17,a,由于A,B两组病人康复时间的方差相等,即波动相同,所以false或18.
试题解析:(1)甲有7种取法,康复时间不少于14天的有3种取法,所以概率false;
(2)如果false,从A,B两组随机各选1人,A组选出的人记为甲,B组选出的人记为乙共有49种取法,甲的康复时间比乙的康复时间长的列举如下:falsefalsefalsefalse有10种取法,所以概率false.
(3)把B组数据调整为a,12,13,14,15,16,17,或12,13,14,15,16,17,a,可见当false或false时,与A组数据方差相等(可利用方差公式加以证明,但本题不需要)
考点:1、古典概型;2、样本的方差
19.【详解】(1)证明:因为平面false平面false,且平面false平面false.
又false,所以false平面false,所以false.
又false,所以false面false.
又false平面false,所以false.
又因为M为false中点,false,所以false,且false.
所以false平面false,又false平面false,
所以平面false面false.
(2)false 可证false为所求的二面角的平面角
20.解(1)由false,得false,又false,
所以false,解得false(负值舍去).
(2)由(1)知,false,在false中,false,在false中,false,又false,所以false,即false.
在false中,false,所以false,
所以false.
21.【答案】(1)证明见解析;(2)false.
【分析】
(1)由线面平行性质得false,再根据对角线互相平分可证;
(2)连接false,通过证明false平面false,可得false为直线false与平面false所成的角,即可得证.
【详解】
(1)连接false,因为false平面false,平面false平面false,false平面false,所以false,
由F为线段false的中点,可知E为线段false的中点,
又E为线段false的中点,所以四边形false为平行四边形.
(2)如图,连接false,
由(1)及false是边长为2的等边三角形可知,平行四边形false为菱形,且false.
易知四边形false为菱形,又false,所以false.
又false,所以false平面false,所以false.
因为false,所以false.
因为false,平面false平面false,平面false平面false,所以false平面false,
所以false,又E为false的中点,false,
所以false,false,
又false,所以false平面false,
故false为直线false与平面false所成的角.
易知false,故false.
故直线false与平面false所成角的正弦值为false.
【点睛】
关键点睛:解决本题的关键是正确理解线面角的定义,作出恰当的辅助角,找到正确的线面角.
22.【答案】
(1)false
(2)甲组研发新药的贡献效益依次为5,5,5,false,false,5,5,5,false,5,false,5,5,false,5.
则甲组贡献经济效益金的平均值false(万元).
乙组研发新药的贡献效益依次为5,false,5,5,false,5,5,false,5,false,false,5,false,5,5.
则乙组贡献经济效益金的平均值false(万元).
(3)甲组获得奖金额依次为1,1,1,0,0,1,1,1,0,1,0,1,1,0,1(千元),
甲组获得资金的平均值false(千元),甲组获得资金的方差
false.
乙组获得奖金额依次为1,0,1,1,0,1,1,0,1,0,0,1,0,1,1(千元)
乙组获得奖金的平均值false(千元),乙组获得奖金的方差
false.
从而可以确定false;但false,
综上所述,从所得数据看,甲组的研发水平应高于乙组研发水平.
数学期末试题
第Ⅰ卷(选择题)
一、单选题(每小题5分,共60分)
1.设false,则false( )
A.false B.false C.false D.false
2.电影《我和我的家乡》于2020年10月11日在中国内地上映,到2020年10月14日已累计票房22.33亿,创造了多个票房记录,某新闻机构想了解全国人民对《我和我的家乡》的评价,决定从某市3个区按人口数用分层抽样的方法抽取一个样本.若3个区人口数之比为false,且人口最多的一个区抽出100人,则这个样本的容量等于( )
A.100 B.160 C.200 D.240
3.一个圆锥的侧面展开图是圆心角为false,弧长为false的扇形,则该圆锥轴截面的面积false( )
A.false B.false C.false D.false
4.在普通高中新课程改革中,某地实施“false”选课方案.该方案中“2”指的是从政治、地理、化学、生物4门中任选2门作为选考科目,假设每门科目被选中的可能性相等,那么化学和生物至多有一门被选中的概率是( )
A.false B.false C.false D.false
5.已知在正四面体false中,点E为棱false的中点,则异面直线false与false成角的余弦值为( )
A.false B.false C.false D.false
6.天气预报说,在今后的三天中,每一天下雨的概率均为40%,用数字0,1,2,3表示下雨,数字4,5,6,7,8,9表示不下雨,由计算机产生如下20组随机数:
977,864,191,925,271,932,812,458,569,683,
431,257,394,027,556,488,730,113,537,908.
由此估计今后三天中至少有一天下雨的概率为( )
A.0.6 B.0.7 C.0.75 D.0.8
7.已知false,则false等于( )
A.false B.97 C.false D.61
8.已知在false中,a,b,c分别为内角A,B,C的对边,false,且false,则false( )
A.6 B.10 C.12 D.16
9.2021年是中国共产党建党100周年,为全面贯彻党的教育方针,提高学生的审美水平和人文素养,促进学生全面发展.某学校高一年级举办了班级合唱活动.现从全校学生中随机抽取部分学生,并邀请他们为此次活动评分(单位:分,满分100分),对评分进行整理,得到如图所示的频率分布直方图,则下列结论不正确的是( )
A.false
B.若该学校有3000名学生参与了评分,则估计评分超过90分的学生人数为600
C.学生评分的众数的估计值为85
D.学生评分的中位数的估计值为83
10.设false的内角A、B、C的对边分别是a,b,c,false,且B为钝角.false的取值范围( )
A.false B.false C.false D.false
11.在三棱锥false中,false,则该三棱锥的外接球的表面积为( )
A.false B.false C.false D.false
12.如图,在菱形false中,false,将false沿对角线false翻折到false位置,连结false,则在翻折过程中,下列说法正确的( )个
①.false与平面false所成的最大角为false
②.存在某个位置,使得false
③.当二面角false的大小为false时,false
④.存在某个位置,使得B到平面false的距离为false
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题)
二、填空题(每小题5分,共20分)
13.若一组数据为82,81,79,78,95,88,92,84,则该组数据的75%分位数是______________.
14.为了测量河对岸两点C,D间的距离,现在沿岸相距false的两点A,B处分别测得false,false,false,false,则C,D间的距离为___________.
15.已知正四棱锥false可绕着false任意旋转,false/平面false,若false,则正四棱锥false在面false内的投影面积的取值范围是__________.
16.已知false是两个平面向量,false,且对任意false,恒有false,则false的最大值是__________.
三、解答题(第17题10分,18-22题每题12分,共70分)
17.如图,在平行六面体false中,以顶点A为端点的三条棱长度都为2,且两两夹角为false.
(1)求false的长;(2)求false与false所成角的余弦值.
18.A,B两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
A组:10,11,12,13,14,15,16
B组:12,13,15,16,17,14,a
假设所有病人的康复时间互相独立,从A,B两组随机各选1人,A组选出的人记为甲,B组选出的人记为乙.
(1)求甲的康复时间不少于14天的概率;
(2)如果false,求甲的康复时间比乙的康复时间长的概率;
(3)当a为何值时,A,B两组病人康复时间的方差相等?(结论不要求证明,只写出结果)
19.如图,在四棱锥false中,平面false平面false,四边形false为矩形,false,false,M为false的中点.
(1)求证:平面false平面false;
(2)求二面角false的余弦值.
20.已知false的三个内角A,B,C的对边分别为a,b,c且满足false.
(1)求b的值;
(2)若false平分false交false于点D,求false的面积.
21.如图所示的几何体是由三棱柱false和四棱锥false组合而成的,已知false,线段false与false交于点E,E,F分别为线段false的中点,平面false平面false平面false.
(1)求证:四边形false为平行四边形;
(2)若false是边长为2的等边三角形,false,求直线false与平面false所成角的正弦值.
22.某医学科研单位有甲,乙两个专门从事病毒治愈的研发小组,为了比较他们的研发水平,现随机抽取了这两个小组在过去一年里其中经过15次各自研发的新药结果如下:falsefalse其中false分别表示甲组研发新药成功和失败;false分别表示乙组研发新药成功与失败.(1)根据上面这组数据,计算恰有一组研发新药成功的条件下,甲,乙两组同时都研发新药成功的概率.(2)若某组成功研发一种新药,则该组可直接为本单位创造经济价值为5万余元,并且单位奖励给该组1千元,否则就亏损1万余元,奖励0元,试计算甲,乙两组研发新药的经济效益的平均数;
(3)根据(2)的条件分别计算甲乙两组的奖金的方差,并且比较甲乙两组的研发水平;
高一期末数学答案
一、选择题:本题共12小题,每小题5分,共60分.
CCBDAB CBDAAB
二、填空题(每题5分,共20分)
13.90 14.2 15.false 16.4
三、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤
17.(1)false;(2)false
18.【答案】(1)false,(2)false,(3)false或18
【解析】
试题分析:针对甲有7种情况,康复时间不少于14天有3种情况,概率为false;如果false,甲、乙随机各取一人有49种情况,用列举法列出甲的康复时间比乙的康复时间长的情况有10种,概率为false,由于A组数据为10,11,12,13,14,15,16;B组数据调整为a,12,13,14,15,16,17,或12,13,14,15,16,17,a,由于A,B两组病人康复时间的方差相等,即波动相同,所以false或18.
试题解析:(1)甲有7种取法,康复时间不少于14天的有3种取法,所以概率false;
(2)如果false,从A,B两组随机各选1人,A组选出的人记为甲,B组选出的人记为乙共有49种取法,甲的康复时间比乙的康复时间长的列举如下:falsefalsefalsefalse有10种取法,所以概率false.
(3)把B组数据调整为a,12,13,14,15,16,17,或12,13,14,15,16,17,a,可见当false或false时,与A组数据方差相等(可利用方差公式加以证明,但本题不需要)
考点:1、古典概型;2、样本的方差
19.【详解】(1)证明:因为平面false平面false,且平面false平面false.
又false,所以false平面false,所以false.
又false,所以false面false.
又false平面false,所以false.
又因为M为false中点,false,所以false,且false.
所以false平面false,又false平面false,
所以平面false面false.
(2)false 可证false为所求的二面角的平面角
20.解(1)由false,得false,又false,
所以false,解得false(负值舍去).
(2)由(1)知,false,在false中,false,在false中,false,又false,所以false,即false.
在false中,false,所以false,
所以false.
21.【答案】(1)证明见解析;(2)false.
【分析】
(1)由线面平行性质得false,再根据对角线互相平分可证;
(2)连接false,通过证明false平面false,可得false为直线false与平面false所成的角,即可得证.
【详解】
(1)连接false,因为false平面false,平面false平面false,false平面false,所以false,
由F为线段false的中点,可知E为线段false的中点,
又E为线段false的中点,所以四边形false为平行四边形.
(2)如图,连接false,
由(1)及false是边长为2的等边三角形可知,平行四边形false为菱形,且false.
易知四边形false为菱形,又false,所以false.
又false,所以false平面false,所以false.
因为false,所以false.
因为false,平面false平面false,平面false平面false,所以false平面false,
所以false,又E为false的中点,false,
所以false,false,
又false,所以false平面false,
故false为直线false与平面false所成的角.
易知false,故false.
故直线false与平面false所成角的正弦值为false.
【点睛】
关键点睛:解决本题的关键是正确理解线面角的定义,作出恰当的辅助角,找到正确的线面角.
22.【答案】
(1)false
(2)甲组研发新药的贡献效益依次为5,5,5,false,false,5,5,5,false,5,false,5,5,false,5.
则甲组贡献经济效益金的平均值false(万元).
乙组研发新药的贡献效益依次为5,false,5,5,false,5,5,false,5,false,false,5,false,5,5.
则乙组贡献经济效益金的平均值false(万元).
(3)甲组获得奖金额依次为1,1,1,0,0,1,1,1,0,1,0,1,1,0,1(千元),
甲组获得资金的平均值false(千元),甲组获得资金的方差
false.
乙组获得奖金额依次为1,0,1,1,0,1,1,0,1,0,0,1,0,1,1(千元)
乙组获得奖金的平均值false(千元),乙组获得奖金的方差
false.
从而可以确定false;但false,
综上所述,从所得数据看,甲组的研发水平应高于乙组研发水平.
同课章节目录
