江苏省南京市秦淮区高中2020-2021学年高二下学期6月月考数学试题 Word版含答案解析
文档属性
| 名称 | 江苏省南京市秦淮区高中2020-2021学年高二下学期6月月考数学试题 Word版含答案解析 |  | |
| 格式 | docx | ||
| 文件大小 | 113.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 11:30:28 | ||
图片预览




文档简介
秦淮区高中2020-2021学年高二下学期6月月考
数学试卷
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案填涂在答题卡相应位置上.
1.已知i为虚数单位,则i2021等于(? ? ?)
A. i B. 1 C. -i D. -1
2.在平面直角坐标系xOy中,椭圆+=1的焦点坐标是(? ? ?)
A. (±1,0) B. (±3,0) C. (0,±1) D. (0,±3)
3.若函数y=x2ex在区间(1-a,a+1)上存在极值点,则实数a的取值范围是( )
A.(3,+∞) B.(1,+∞) C.(-1,+∞) D.(-3,+∞)
4.为参加校园文化节,某班推荐2名男生3名女生参加文艺技能培训,培训项目及人数分别为:乐器1人,舞蹈2人,演唱2人.若每人只参加1个项目,并且舞蹈和演唱项目必须有女生参加,则不同推荐方案的种数为( )
A. 12 B. 24 C. 36 D. 48
5.函数y=xcosx-sinx在下面哪个区间内是增函数(???? )
A. (,) B. (π,2π) C.(,) D. (2π,3π)
6.已知某人射击一次命中目标的概率为,且每次射击相互独立,则此人射击7次,有4次命中且恰有3次连续命中的概率为( )
A. C()7 B.C()7 C.C()7 D. A()7
7.已知函数f(x)=x-sinx,则不等式f(x+1)+f(2-2x)>0的解集是( )
A. (-∞,-) B.(3,+∞) C. (-,+∞) D. (-∞,3)
8.法国的数学家费马(Pierrede Fermat)曾在一本数学书的空白处写下一个看起来很简单的猜想:当整数n>2时,找不到满足xn+yn=zn的正整数解.该定理史称费马最后定理,也被称为费马大定理.现任取x,y,z,n∈{1,2,3,4,5},则等式xn+yn=zn成立的概率为(??? )
A. B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,请把答案填涂在答题卡相应位置上.全部选对得5分,部分选对得2分,不选或有错选的得0分.
9.在一个袋中装有质地大小一样的6黑球,4个白球,现从中任取4个小球,设取出的4个小球中白球的个数为X,则下列结论正确的是( )
A. P(X=2)= B. 随机变量X服从二项分布
C. 随机变量X服从超几何分布 D.E(X)=
10.已知三个数1,a,9成等比数列,则圆锥曲线+=1的离心率为( )??
A. B. C. D.
11.某校高二年级进行选课走班,已知语文?数学?英语是必选学科,另外需要从物理?化学?生物?政治?历史?地理6门学科中任选3门进行学习.现有甲?乙?丙三人,若同学甲必选物理,则下列结论正确的是(? ? )
A. 甲选课的不同的选法种数为10
B. 甲?乙?丙三人至少一人选化学与这三人全选化学是对立事件
C. 乙同学在选物理的条件下选化学的概率是
D. 乙?丙两名同学都选物理的概率是
12.已知函数f(x)=ln|x|-x+,给出下列四个结论,其中正确的是(??? )
A. 曲线y=f(x)在x=1处的切线方程为x+y+1=0
B. f(x)恰有2个零点
C. f(x)既有最大值,又有最小值
D. 若x1x2>0且f(x1)+f(x2)=0,则x1x2=1
三、填空题:本大题共4小题,每小题5分,共20分.请把答案填写在答题卡相应位置上.
13.若曲线y=ax2在点(1,a)处的切线与直线x+2y-6=0垂直,则实数a的值为______.
14.若z∈C,且|z+3+4i|≤2,则|z|的取值范围为____________.
15.若对任意实数x,y都有(x-2y)5=a0(x+2y)5+a1(x+2y)4y+a2(x+2y)3y2+
a3(x+2y)2y3+a4(x+2y)y4+a5y5,则a0+a1+a2+a3+a4+a5的值为______.
16.已知函数f(x)=(x+1)sinx+cosx,若对于任意的x1,x2∈[0,](x1≠x2),均有
|f(x1)-f(x2)|<a|e-e|成立,则实数a的取值范围为________.
四、解答题:本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出必要的文字说明,证明过程或演算步骤.
17.(本小题共10分)
为了普及安全教育,某市组织了一次学生安全知识竞赛,规定每队3人,每人回答一个问题,答对得1分,答错得0分.在竞赛中,甲?乙两个中学代表队狭路相逢,假设甲队每人回答问题正确的概率均为,乙队每人回答问题正确的概率分别为,,,且两队各人回答问题正确与否相互之间没有影响.
(1)分别求甲队总得分为3分与1分的概率;
(2)求乙队总得分为1分的概率.
18.(本小题共12分)
若(+)n的二项式展开式中前三项的系数和为163,求:
(1)该二项式展开式中所有的有理项;
(2)该二项式展开式中系数最大的项.
19.(本小题共12分)
403415518415如图,在正四棱柱ABCD-A1 B1 C1 D1中,AA1=2,AB=1,点N是BC的中点,点M在线段CC1上(不含端点).设二面角A1-DN-M的大小为θ.
(1)当θ=90°时,求AM的长;
(2)当cos θ=时,求CM的长.
20.(本小题共12分)
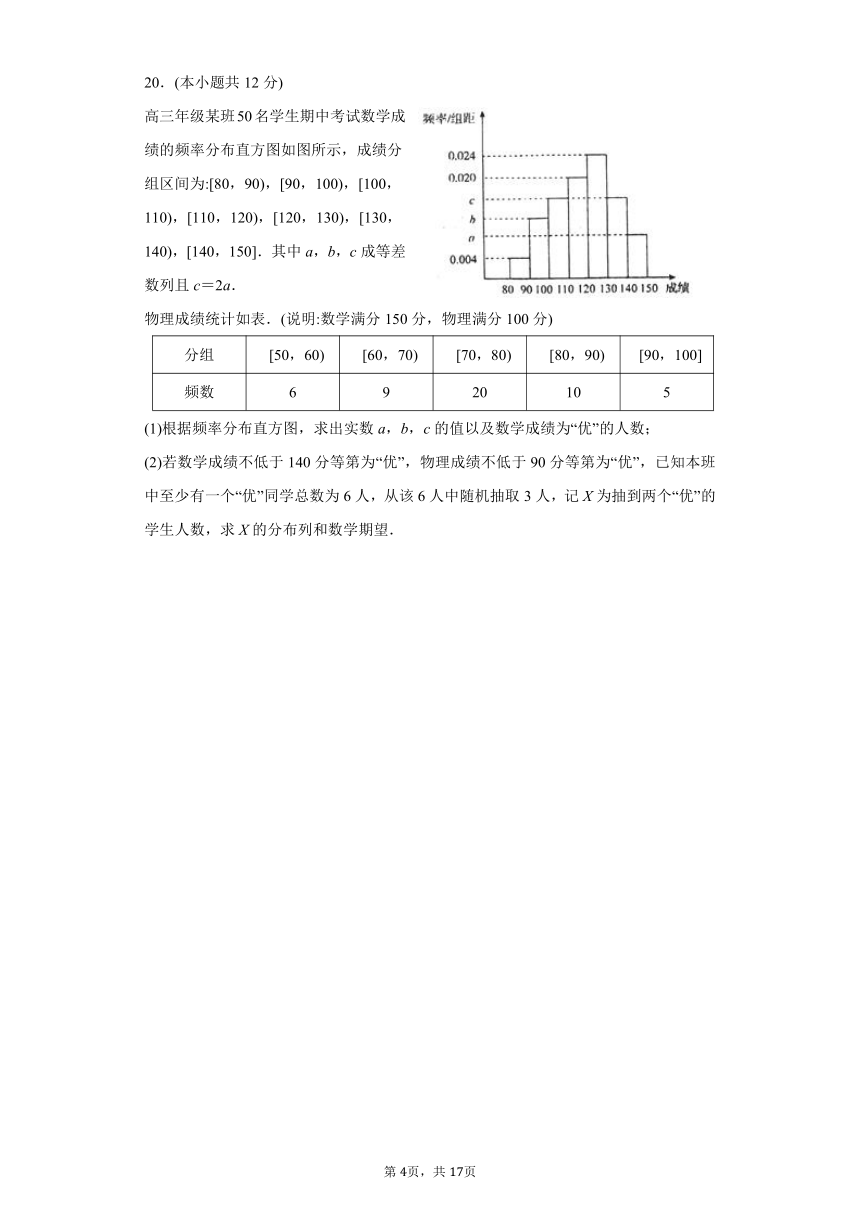
241490573025高三年级某班50名学生期中考试数学成绩的频率分布直方图如图所示,成绩分组区间为:[80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150].其中a,b,c成等差数列且c=2a.
物理成绩统计如表.(说明:数学满分150分,物理满分100分)
分组
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
频数
6
9
20
10
5
(1)根据频率分布直方图,求出实数a,b,c的值以及数学成绩为“优”的人数;
(2)若数学成绩不低于140分等第为“优”,物理成绩不低于90分等第为“优”,已知本班中至少有一个“优”同学总数为6人,从该6人中随机抽取3人,记X为抽到两个“优”的学生人数,求X的分布列和数学期望.
21.(本小题共12分)
已知函数f(x)=2x3-ax2+1(a∈R).
(1)若a=3,求函数f(x)的单调区间;
(2)当a>0时,若函数f(x)在[-1,1]上的最大值和最小值的和为1,求实数a的值.
22.(本小题共12分)
已知函数f(x)=ax--lnx(a∈R).
(1)若f(x)是定义域上的增函数,求a的取值范围;
(2)当a>时,若函数f(x)有两个极值点x1,x2(x1<x2),求f(x1)-f(x2)的取值范围.
秦淮区高中2020-2021学年高二下学期6月月考
数学试卷
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案填涂在答题卡相应位置上.
1.已知i为虚数单位,则i2021等于(? ? ?)
A. i B. 1 C. -i D. -1
【答案】A
【解析】i2021=(i4)505·i=i.
故选A.
2.在平面直角坐标系xOy中,椭圆+=1的焦点坐标是(? ? ?)
A. (±1,0) B. (±3,0) C. (0,±1) D. (0,±3)
【答案】C
【解析】由已知:a2=5,b2=4,
∴c2=1,c=1,且焦点在y轴上,
所以焦点为(0,±1),
故选C.
3.若函数y=x2ex在区间(1-a,a+1)上存在极值点,则实数a的取值范围是( )
A.(3,+∞) B.(1,+∞) C.(-1,+∞) D.(-3,+∞)
【答案】B
【解析】函数y=x2ex的导数为y′=2xex+x2ex=xex(x+2),
令y′=0,则x=0或x=-2,
当x∈(-2,0)时,f(x)单调递减,
当x∈(-∞,-2)和x∈(0,+∞)时,f(x)单调递增,
所以0和-2是函数f(x)的极值点,
因为函数f(x)=x2ex在区间(1-a,a+1)上存在极值点,
所以1-a<-2<a+1或1-a<0<a+1,
解得a>1,
故选B.
4.为参加校园文化节,某班推荐2名男生3名女生参加文艺技能培训,培训项目及人数分别为:乐器1人,舞蹈2人,演唱2人.若每人只参加1个项目,并且舞蹈和演唱项目必须有女生参加,则不同推荐方案的种数为( )
A. 12 B. 24 C. 36 D. 48
【答案】B
【解析】第一类:3名女生各参加1项,2名男生在舞蹈?演唱中各参加1项,有AA=12种方案;
第二类:有2名女生参加同一项,有CAA=12种方案.
所以共有12+12=24种方案.
故选B.
5.函数y=xcosx-sinx在下面哪个区间内是增函数(???? )
A. (,) B. (π,2π) C.(,) D. (2π,3π)
【答案】B
【解析】令f(x)=xcosx-sinx,则f'(x)=cosx-xsinx-cosx=-xsinx,
可得x∈(2kπ+π,2kπ+2π),k∈N,
结合选项可知B正确,
故选B.
6.已知某人射击一次命中目标的概率为,且每次射击相互独立,则此人射击7次,有4次命中且恰有3次连续命中的概率为( )
A. C()7 B.C()7 C.C()7 D. A()7
【答案】D
【解析】先排3次不中的有C=1种排法,其中3次不中有4个空,
在这4个空中分别插入3次连中和1次中的有A中排法,
∵射击一次命中目标的概率为,且每次射击相互独立,则此人射击7次,
∴此人射击7次,有4次命中且恰有3次连续命中的概率为P=A()7.
故选D.
7.已知函数f(x)=x-sinx,则不等式f(x+1)+f(2-2x)>0的解集是( )
A. (-∞,-) B.(3,+∞) C. (-,+∞) D. (-∞,3)
【答案】D
【解析】∵f(x)=x-sinx,
∴f(-x)=-x+sinx=-f(x),即函数f(x)为奇函数,
函数的导数f'(x)=1-cosx≥0恒成立,
则函数f(x)在R上是增函数,
则不等式f(x+1)+f(2-2x)>0等价为f(x+1)>-f(2-2x)=f(2x-2),
即x+1>2x-2,
解得x<3,
故不等式的解集为(-∞,3).
故选D.
8.法国的数学家费马(Pierrede Fermat)曾在一本数学书的空白处写下一个看起来很简单的猜想:当整数n>2时,找不到满足xn+yn=zn的正整数解.该定理史称费马最后定理,也被称为费马大定理.现任取x,y,z,n∈{1,2,3,4,5},则等式xn+yn=zn成立的概率为(??? )
A. B. C. D.
【答案】C
【解析】x,y,z,n∈{1,2,3,4,5},则基本事件的总数为54=625,
当n>2时,由费马大定理知等式xn+yn=zn不成立;
当n=2时,(x,y,z)可取(3,4,5),(4,3,5),共2种情况;
当n=1时,(x,y,z)可取(1,1,2),(1,2,3),(2,1,3),(2,2,4),(1,3,4),(3,1,4),(1,4,5),(4,1,5),(2,3,5),(3,2,5)总10种情况,
∴使等式成立的基本事件个数为12,故等式成立的概率为.
故选C.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,请把答案填涂在答题卡相应位置上.全部选对得5分,部分选对得2分,不选或有错选的得0分.
9.在一个袋中装有质地大小一样的6黑球,4个白球,现从中任取4个小球,设取出的4个小球中白球的个数为X,则下列结论正确的是( )
A. P(X=2)= B. 随机变量X服从二项分布
C. 随机变量X服从超几何分布 D.E(X)=
【答案】ACD
【解析】由题意知:随机变量X服从超几何分布,因此B错误,C正确;
随机变量X的所有可能取值为0,1,2,3,4,
P(X=0)==,P(X=1)==,
P(X=2)==,P(X=3)==,
P(X=4)==,
X
0
1
2
3
4
p
E(X)==,所以A与D都正确.
故选ACD.
10.已知三个数1,a,9成等比数列,则圆锥曲线+=1的离心率为( )??
A. B. C. D.
【答案】BC
【解析】∵三个数1,a,9成等比数列,
∴a2=9,则a=±3,
当a=3时,曲线方程为+=1,表示椭圆,
则长半轴长为,半焦距为1,
离心率为;
当a=-3时,曲线方程为-=1,表示双曲线,
则实半轴长为,半焦距为,
离心率为=.
故选BC.
11.某校高二年级进行选课走班,已知语文?数学?英语是必选学科,另外需要从物理?化学?生物?政治?历史?地理6门学科中任选3门进行学习.现有甲?乙?丙三人,若同学甲必选物理,则下列结论正确的是(? ? )
A. 甲选课的不同的选法种数为10
B. 甲?乙?丙三人至少一人选化学与这三人全选化学是对立事件
C. 乙同学在选物理的条件下选化学的概率是
D. 乙?丙两名同学都选物理的概率是
【答案】AD
【解析】A项:由于甲必选物理,故只需从剩下5门课中选两门即可,即C=10种选法,故A正确;
B项:甲?乙?丙三人至少一人选化学与全不选化学是对立事件,故B错误;
C项:由于乙同学选了物理,乙同学选化学的概率是=,故C错误;
D项:因为乙?丙两名同学各自选物理的概率为=,
所以乙?丙两名同学都选物理的概率是×=,故D正确,
故选AD.
12.已知函数f(x)=ln|x|-x+,给出下列四个结论,其中正确的是(??? )
A. 曲线y=f(x)在x=1处的切线方程为x+y+1=0
B. f(x)恰有2个零点
C. f(x)既有最大值,又有最小值
D. 若x1x2>0且f(x1)+f(x2)=0,则x1x2=1
【答案】BD
【解析】
对于A,当x>0时,
由于函数f(x)=lnx-x+,所以f'(x)=--1,
所以f(1)=0,f'(1)=--1=-1,
所以曲线y=f(x)在x=1处的切线方程为y=-1(x-1),即x+y-1=0,故A错误;
对于B?C,因为x>0时,f'(x)=<0,
所以f(x)在区间(0,+∞)上单调递减.
同理可求f(x)在区间(-∞,0)上单调递减,所以C错误;
又f(-1)=0,f(1)=0,
所以f(x)恰有2个零点,所以B正确;
对于D,若x1>0,x2>0,由f(x1)+f(x2)=0,
得f(x1)=-f(x2)=-(lnx2-x2+)=ln+-=f(),
即f(x1)=f().
因为f(x)在(0,+∞)上单调递减,所以x1=,即x1x2=1.
同理可证当x1<0,x2<0时,命题也成立.故D正确.
故选BD.
三、填空题:本大题共4小题,每小题5分,共20分.请把答案填写在答题卡相应位置上.
13.若曲线y=ax2在点(1,a)处的切线与直线x+2y-6=0垂直,则实数a的值为______.
【答案】1
【解析】由y=ax2,得y'=2ax,y'|x=1=2a,
∵曲线y=ax2在点(1,a)处的切线与直线x+2y-6=0垂直,
∴2a=2,a=1.
故答案为:1.
14.若z∈C,且|z+3+4i|≤2,则|z|的取值范围为____________.
【答案】[3,7]
【解析】设z=x+yi,(x,y∈R),
则|z+3+4i|=|(x+3)+(y+4)i|=≤2,
所以点z是复平面内以(-3,-4)为圆心,2为半径的圆上或圆内的点;
|z|=表示点z到原点的距离,|OC|==5,
OA=5-2=3为最小值,OB=5+2=7最大值,故取值范围为[3,7].
故答案为[3,7].
15.若对任意实数x,y都有(x-2y)5=a0(x+2y)5+a1(x+2y)4y+a2(x+2y)3y2+
a3(x+2y)2y3+a4(x+2y)y4+a5y5,则a0+a1+a2+a3+a4+a5的值为______.
【答案】-243
【解析】根据系数之间的关系,令x+2y=1,y=1,∴x=-1,y=1,∴a0+a1+a2+a3+a4+a5=(-3)5=-243,故答案为-243.
16.已知函数f(x)=(x+1)sinx+cosx,若对于任意的x1,x2∈[0,](x1≠x2),均有
|f(x1)-f(x2)|<a|e-e|成立,则实数a的取值范围为________.
【答案】[1,+∞)
【解析】由题意,函数f(x)=xsinx+sinx+cosx,
求导得f'(x)=xcosx+cosx=(x+1)cosx,
则由x∈[0,]可知f'(x)≥0恒成立,故f(x)在x∈[0,]单调递增,
不妨设x1<x2,则|f(x1)-f(x2)|=f(x2)-f(x1),|e-e|=e-e,
从而有f(x2)-f(x1)<a(e-e)恒成立,
即f(x2)-ae<f(x1)-ae恒成立,
设g(x)=f(x)-aex,则g(x)在x∈[0,]单调递减,
所以g'(x)=(x+1)cosx-aex≤0恒成立,
整理得a≥恒成立,设h(x)=,求导得,h'(x)=≤0,,所以h(x)=单调递减,则要a≥()max恒成立,
只要a≥h(0)=1,故答案为[1,+∞).
四、解答题:本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出必要的文字说明,证明过程或演算步骤.
17.(本小题共10分)
为了普及安全教育,某市组织了一次学生安全知识竞赛,规定每队3人,每人回答一个问题,答对得1分,答错得0分.在竞赛中,甲?乙两个中学代表队狭路相逢,假设甲队每人回答问题正确的概率均为,乙队每人回答问题正确的概率分别为,,,且两队各人回答问题正确与否相互之间没有影响.
(1)分别求甲队总得分为3分与1分的概率;
(2)求乙队总得分为1分的概率.
【答案】(1)记“甲队总得分为3分”为事件A,记“甲队总得分为1分”为事件B.
甲队得3分,即三人都回答正确,其概率P(A)=××=. 3分
甲队得1分,即三人中只有1人答对,其余两人都答错,
其概率P(B)=×(1-)×(1-)+(1-)××(1-)+(1-)×(1-)×
=C××()2=. 6分
答:甲队总得分为3分的概率为,甲队总得分为1分的概率为.
(2)记“乙队总得分为1分”为事件C.
事件C即乙队3人中只有1人答对,其余2人答错,
则P(C)=×(1-)×(1-)+(1-)××(1-)+(1-)×(1-)×=. 10分
答:乙队总得分为1分的概率为.
18.(本小题共12分)
若(+)n的二项式展开式中前三项的系数和为163,求:
(1)该二项式展开式中所有的有理项;
(2)该二项式展开式中系数最大的项.
【答案】展开式前三项的系数为1,2C,4C.
由题意得1+2C+4C=163,整理得n2=81,所以n=9. 2分
(1)设展开式中的有理项为Tk+1,
由Tk+1=C()9-k()k=2kCx,
又∵0≤k≤9,∴k=2或6.
故有理项为T3=22C·x=144x3,T7=26·C·x=5376. 6分
(2)设展开式中Tk+1项的系数最大,
则
∴≤k≤,又∵k∈N,∴k=6,
故展开式中系数最大的项为T7=5376. 12分
19.(本小题共12分)
403415518415如图,在正四棱柱ABCD-A1 B1 C1 D1中,AA1=2,AB=1,点N是BC的中点,点M在线段CC1上(不含端点).设二面角A1-DN-M的大小为θ.
(1)当θ=90°时,求AM的长;
(2)当cos θ=时,求CM的长.
解:建立如图所示的空间直角坐标系D-xyz.设CM=t(0 398018090805则各点的坐标为A(1,0,0),A1(1,0,2),N(,1,0),M(0,1,t).
所以=(,1,0),=(0,1,t),=(1,0,2).
设平面DMN的法向量为n1=(x1,y1,z1),则n1·=0,n1·=0.
即x1+2 y1=0,y1+ tz1=0,令z1=1,则y1=- t,x1=2 t.
所以n1=(2t,-t,1)是平面DMN的一个法向量. 3分
设平面A1 DN的法向量为n2=(x2,y2,z2),则
n2·=0,n2·=0.即x2+2 z2=0,x2+2 y2=0.
令z2=1,则x2=-2,y2=1.
所以n2=(-2,1,1)是平面A1 DN的一个法向量. 6分
从而n1·n2=-5 t+1.
(1)因为θ=90°,所以n1·n2=-5 t+1=0,解得t=.从而M(0,1,).
所以AM==. 8分
(2)因为|n1|=,|n2|=,
所以cos<n1,n2>==.
因为<n1,n2>=θ或π-θ,所以||=,解得t=0或t=.
所以t=,从而CM的长为. 12分
20.(本小题共12分)
241490573025高三年级某班50名学生期中考试数学成绩的频率分布直方图如图所示,成绩分组区间为:[80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150].其中a,b,c成等差数列且c=2a.
物理成绩统计如表.(说明:数学满分150分,物理满分100分)
分组
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
频数
6
9
20
10
5
(1)根据频率分布直方图,求出实数a,b,c的值以及数学成绩为“优”的人数;
(2)若数学成绩不低于140分等第为“优”,物理成绩不低于90分等第为“优”,已知本班中至少有一个“优”同学总数为6人,从该6人中随机抽取3人,记X为抽到两个“优”的学生人数,求X的分布列和数学期望.
【答案】解:(1)由于a+b+2c=0.052,a+c=2b,c=2a,
解得a=0.008,b=0.012,c=0.016,
数学成绩为“优”的人数:50×a×10=4(人) 4分
(2)数学成绩为“优”的同学有4人,物理成绩为“优”有5人,
因为至少有一个“优”的同学总数为6名同学,
故两科均为“优”的人数为3人, 6分
故X的取值为0?1?2?3.
P(X=0)==,P(x=1)==,
P(X=2)==,P(X=3)==.
X
0
1
2
3
P
?
?
?
E(X)=0×+1×+2×+3×=. 12分
21.(本小题共12分)
已知函数f(x)=2x3-ax2+1(a∈R).
(1)若a=3,求函数f(x)的单调区间;
(2)当a>0时,若函数f(x)在[-1,1]上的最大值和最小值的和为1,求实数a的值.
【答案】解:(1) f(x)=2x3-ax2+1,令f'(x)=6x2-2ax=2x(3x-a)=0,得x1=0,x2=1,
当a=3时,由f'(x)>0得x<0或x>1,即函数f(x)在(-∞,0)和(1,+∞)上单调递增,
由f'(x)<0得0<x<1,即函数f(x)在(0,1)上单调递减,
所以函数f(x)的单调递增区间为(-∞,0),(1,+∞),单调递减区间为(0,1). 4分
(2)当a>0时,函数f(x)在(-∞,0),(,+∞)上单调递增,在(0,)上单调递减,
此时函数f(x)有两个极值点,极大值为f(0)=1,极小值为f()=1-,
且f(-1)=-a-1,f(1)=3-a.
1若≥1,即a≥3时,f(x)max=f(0)=1,此时f(-1)<f(1),所以f(x)min=f(-1)=-a-1,
由f(x)max+f(x)min=1可得1+(-a-1)=1,即a=-1,不符合题意,舍去. 6分
2若0<<1,即0<a<3时,比较f(1)与f(0)的大小.
①若f(1)≥f(0),即3-a≥1,也即0<a≤2时,此时f(x)max=f(1)=3-a,
又因为f()=1->0,f(-1)=-a-1<0,所以f(x)min=f(-1)=-1-a,
由f(x)max+f(x)min=1可得(3-a)+(-1-a)=1,即a=,符合题意. 9分
②若f(1)<f(0),即3-a<1,即2<a<3时,此时f(x)max=f(0)=1.
又因为f()=1->0,f(-1)=-a-1<0,所以f(x)min=f(-1)=-1-a,
由f(x)max+f(x)min=1可得1+(-1-a)=1,即a=-1,不符合题意.
综上所述,所求实数a的值为. 12分
22.(本小题共12分)
已知函数f(x)=ax--lnx(a∈R).
(1)若f(x)是定义域上的增函数,求a的取值范围;
(2)当a>时,若函数f(x)有两个极值点x1,x2(x1<x2),求f(x1)-f(x2)的取值范围.
【答案】解:(1)f(x)的定义域为(0,+∞),f'(x)=a+-=,
∵f(x)在定义域内单调递增,
∴f'(x)≥0,即ax2-x+a≥0对x>0恒成立,
则a≥恒成立,∴a≥()max,
∵=≤=,
当且仅当x=1时上式取等,∴a≥,
所以,a的取值范围是[,+∞). 3分
(2)设方程f'(x)=0,即ax2-x+a=0的两根为x1,x2,且0<x1<x2,
由Δ=1-4a2>0且a>,得<a<,
∵x1x2=1,x1+x2=, 5分
∴2<x1+=<,∴<x1<1,
f(x1)-f(x2)=ax1--lnx1-(ax2--lnx2)
=ax1--lnx1-(-ax1+lnx1)=2(ax1--lnx1),
∵ax12-x1+a=0,
∴a=代入得f(x1)-f(x2)=2(-lnx1)=2(-lnx12), 8分
令x12=t,则<t<1,
令g(t)=-lnt,<t<1,g'(t)=<0,
∴g(t)在(,1)上递减,从而g(1)<g(t)<g(),
即0<g(t)<-+ln2,所以f(x1)-f(x2)的取值范围为(0,-+2ln2). 12分
数学试卷
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案填涂在答题卡相应位置上.
1.已知i为虚数单位,则i2021等于(? ? ?)
A. i B. 1 C. -i D. -1
2.在平面直角坐标系xOy中,椭圆+=1的焦点坐标是(? ? ?)
A. (±1,0) B. (±3,0) C. (0,±1) D. (0,±3)
3.若函数y=x2ex在区间(1-a,a+1)上存在极值点,则实数a的取值范围是( )
A.(3,+∞) B.(1,+∞) C.(-1,+∞) D.(-3,+∞)
4.为参加校园文化节,某班推荐2名男生3名女生参加文艺技能培训,培训项目及人数分别为:乐器1人,舞蹈2人,演唱2人.若每人只参加1个项目,并且舞蹈和演唱项目必须有女生参加,则不同推荐方案的种数为( )
A. 12 B. 24 C. 36 D. 48
5.函数y=xcosx-sinx在下面哪个区间内是增函数(???? )
A. (,) B. (π,2π) C.(,) D. (2π,3π)
6.已知某人射击一次命中目标的概率为,且每次射击相互独立,则此人射击7次,有4次命中且恰有3次连续命中的概率为( )
A. C()7 B.C()7 C.C()7 D. A()7
7.已知函数f(x)=x-sinx,则不等式f(x+1)+f(2-2x)>0的解集是( )
A. (-∞,-) B.(3,+∞) C. (-,+∞) D. (-∞,3)
8.法国的数学家费马(Pierrede Fermat)曾在一本数学书的空白处写下一个看起来很简单的猜想:当整数n>2时,找不到满足xn+yn=zn的正整数解.该定理史称费马最后定理,也被称为费马大定理.现任取x,y,z,n∈{1,2,3,4,5},则等式xn+yn=zn成立的概率为(??? )
A. B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,请把答案填涂在答题卡相应位置上.全部选对得5分,部分选对得2分,不选或有错选的得0分.
9.在一个袋中装有质地大小一样的6黑球,4个白球,现从中任取4个小球,设取出的4个小球中白球的个数为X,则下列结论正确的是( )
A. P(X=2)= B. 随机变量X服从二项分布
C. 随机变量X服从超几何分布 D.E(X)=
10.已知三个数1,a,9成等比数列,则圆锥曲线+=1的离心率为( )??
A. B. C. D.
11.某校高二年级进行选课走班,已知语文?数学?英语是必选学科,另外需要从物理?化学?生物?政治?历史?地理6门学科中任选3门进行学习.现有甲?乙?丙三人,若同学甲必选物理,则下列结论正确的是(? ? )
A. 甲选课的不同的选法种数为10
B. 甲?乙?丙三人至少一人选化学与这三人全选化学是对立事件
C. 乙同学在选物理的条件下选化学的概率是
D. 乙?丙两名同学都选物理的概率是
12.已知函数f(x)=ln|x|-x+,给出下列四个结论,其中正确的是(??? )
A. 曲线y=f(x)在x=1处的切线方程为x+y+1=0
B. f(x)恰有2个零点
C. f(x)既有最大值,又有最小值
D. 若x1x2>0且f(x1)+f(x2)=0,则x1x2=1
三、填空题:本大题共4小题,每小题5分,共20分.请把答案填写在答题卡相应位置上.
13.若曲线y=ax2在点(1,a)处的切线与直线x+2y-6=0垂直,则实数a的值为______.
14.若z∈C,且|z+3+4i|≤2,则|z|的取值范围为____________.
15.若对任意实数x,y都有(x-2y)5=a0(x+2y)5+a1(x+2y)4y+a2(x+2y)3y2+
a3(x+2y)2y3+a4(x+2y)y4+a5y5,则a0+a1+a2+a3+a4+a5的值为______.
16.已知函数f(x)=(x+1)sinx+cosx,若对于任意的x1,x2∈[0,](x1≠x2),均有
|f(x1)-f(x2)|<a|e-e|成立,则实数a的取值范围为________.
四、解答题:本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出必要的文字说明,证明过程或演算步骤.
17.(本小题共10分)
为了普及安全教育,某市组织了一次学生安全知识竞赛,规定每队3人,每人回答一个问题,答对得1分,答错得0分.在竞赛中,甲?乙两个中学代表队狭路相逢,假设甲队每人回答问题正确的概率均为,乙队每人回答问题正确的概率分别为,,,且两队各人回答问题正确与否相互之间没有影响.
(1)分别求甲队总得分为3分与1分的概率;
(2)求乙队总得分为1分的概率.
18.(本小题共12分)
若(+)n的二项式展开式中前三项的系数和为163,求:
(1)该二项式展开式中所有的有理项;
(2)该二项式展开式中系数最大的项.
19.(本小题共12分)
403415518415如图,在正四棱柱ABCD-A1 B1 C1 D1中,AA1=2,AB=1,点N是BC的中点,点M在线段CC1上(不含端点).设二面角A1-DN-M的大小为θ.
(1)当θ=90°时,求AM的长;
(2)当cos θ=时,求CM的长.
20.(本小题共12分)
241490573025高三年级某班50名学生期中考试数学成绩的频率分布直方图如图所示,成绩分组区间为:[80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150].其中a,b,c成等差数列且c=2a.
物理成绩统计如表.(说明:数学满分150分,物理满分100分)
分组
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
频数
6
9
20
10
5
(1)根据频率分布直方图,求出实数a,b,c的值以及数学成绩为“优”的人数;
(2)若数学成绩不低于140分等第为“优”,物理成绩不低于90分等第为“优”,已知本班中至少有一个“优”同学总数为6人,从该6人中随机抽取3人,记X为抽到两个“优”的学生人数,求X的分布列和数学期望.
21.(本小题共12分)
已知函数f(x)=2x3-ax2+1(a∈R).
(1)若a=3,求函数f(x)的单调区间;
(2)当a>0时,若函数f(x)在[-1,1]上的最大值和最小值的和为1,求实数a的值.
22.(本小题共12分)
已知函数f(x)=ax--lnx(a∈R).
(1)若f(x)是定义域上的增函数,求a的取值范围;
(2)当a>时,若函数f(x)有两个极值点x1,x2(x1<x2),求f(x1)-f(x2)的取值范围.
秦淮区高中2020-2021学年高二下学期6月月考
数学试卷
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案填涂在答题卡相应位置上.
1.已知i为虚数单位,则i2021等于(? ? ?)
A. i B. 1 C. -i D. -1
【答案】A
【解析】i2021=(i4)505·i=i.
故选A.
2.在平面直角坐标系xOy中,椭圆+=1的焦点坐标是(? ? ?)
A. (±1,0) B. (±3,0) C. (0,±1) D. (0,±3)
【答案】C
【解析】由已知:a2=5,b2=4,
∴c2=1,c=1,且焦点在y轴上,
所以焦点为(0,±1),
故选C.
3.若函数y=x2ex在区间(1-a,a+1)上存在极值点,则实数a的取值范围是( )
A.(3,+∞) B.(1,+∞) C.(-1,+∞) D.(-3,+∞)
【答案】B
【解析】函数y=x2ex的导数为y′=2xex+x2ex=xex(x+2),
令y′=0,则x=0或x=-2,
当x∈(-2,0)时,f(x)单调递减,
当x∈(-∞,-2)和x∈(0,+∞)时,f(x)单调递增,
所以0和-2是函数f(x)的极值点,
因为函数f(x)=x2ex在区间(1-a,a+1)上存在极值点,
所以1-a<-2<a+1或1-a<0<a+1,
解得a>1,
故选B.
4.为参加校园文化节,某班推荐2名男生3名女生参加文艺技能培训,培训项目及人数分别为:乐器1人,舞蹈2人,演唱2人.若每人只参加1个项目,并且舞蹈和演唱项目必须有女生参加,则不同推荐方案的种数为( )
A. 12 B. 24 C. 36 D. 48
【答案】B
【解析】第一类:3名女生各参加1项,2名男生在舞蹈?演唱中各参加1项,有AA=12种方案;
第二类:有2名女生参加同一项,有CAA=12种方案.
所以共有12+12=24种方案.
故选B.
5.函数y=xcosx-sinx在下面哪个区间内是增函数(???? )
A. (,) B. (π,2π) C.(,) D. (2π,3π)
【答案】B
【解析】令f(x)=xcosx-sinx,则f'(x)=cosx-xsinx-cosx=-xsinx,
可得x∈(2kπ+π,2kπ+2π),k∈N,
结合选项可知B正确,
故选B.
6.已知某人射击一次命中目标的概率为,且每次射击相互独立,则此人射击7次,有4次命中且恰有3次连续命中的概率为( )
A. C()7 B.C()7 C.C()7 D. A()7
【答案】D
【解析】先排3次不中的有C=1种排法,其中3次不中有4个空,
在这4个空中分别插入3次连中和1次中的有A中排法,
∵射击一次命中目标的概率为,且每次射击相互独立,则此人射击7次,
∴此人射击7次,有4次命中且恰有3次连续命中的概率为P=A()7.
故选D.
7.已知函数f(x)=x-sinx,则不等式f(x+1)+f(2-2x)>0的解集是( )
A. (-∞,-) B.(3,+∞) C. (-,+∞) D. (-∞,3)
【答案】D
【解析】∵f(x)=x-sinx,
∴f(-x)=-x+sinx=-f(x),即函数f(x)为奇函数,
函数的导数f'(x)=1-cosx≥0恒成立,
则函数f(x)在R上是增函数,
则不等式f(x+1)+f(2-2x)>0等价为f(x+1)>-f(2-2x)=f(2x-2),
即x+1>2x-2,
解得x<3,
故不等式的解集为(-∞,3).
故选D.
8.法国的数学家费马(Pierrede Fermat)曾在一本数学书的空白处写下一个看起来很简单的猜想:当整数n>2时,找不到满足xn+yn=zn的正整数解.该定理史称费马最后定理,也被称为费马大定理.现任取x,y,z,n∈{1,2,3,4,5},则等式xn+yn=zn成立的概率为(??? )
A. B. C. D.
【答案】C
【解析】x,y,z,n∈{1,2,3,4,5},则基本事件的总数为54=625,
当n>2时,由费马大定理知等式xn+yn=zn不成立;
当n=2时,(x,y,z)可取(3,4,5),(4,3,5),共2种情况;
当n=1时,(x,y,z)可取(1,1,2),(1,2,3),(2,1,3),(2,2,4),(1,3,4),(3,1,4),(1,4,5),(4,1,5),(2,3,5),(3,2,5)总10种情况,
∴使等式成立的基本事件个数为12,故等式成立的概率为.
故选C.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,请把答案填涂在答题卡相应位置上.全部选对得5分,部分选对得2分,不选或有错选的得0分.
9.在一个袋中装有质地大小一样的6黑球,4个白球,现从中任取4个小球,设取出的4个小球中白球的个数为X,则下列结论正确的是( )
A. P(X=2)= B. 随机变量X服从二项分布
C. 随机变量X服从超几何分布 D.E(X)=
【答案】ACD
【解析】由题意知:随机变量X服从超几何分布,因此B错误,C正确;
随机变量X的所有可能取值为0,1,2,3,4,
P(X=0)==,P(X=1)==,
P(X=2)==,P(X=3)==,
P(X=4)==,
X
0
1
2
3
4
p
E(X)==,所以A与D都正确.
故选ACD.
10.已知三个数1,a,9成等比数列,则圆锥曲线+=1的离心率为( )??
A. B. C. D.
【答案】BC
【解析】∵三个数1,a,9成等比数列,
∴a2=9,则a=±3,
当a=3时,曲线方程为+=1,表示椭圆,
则长半轴长为,半焦距为1,
离心率为;
当a=-3时,曲线方程为-=1,表示双曲线,
则实半轴长为,半焦距为,
离心率为=.
故选BC.
11.某校高二年级进行选课走班,已知语文?数学?英语是必选学科,另外需要从物理?化学?生物?政治?历史?地理6门学科中任选3门进行学习.现有甲?乙?丙三人,若同学甲必选物理,则下列结论正确的是(? ? )
A. 甲选课的不同的选法种数为10
B. 甲?乙?丙三人至少一人选化学与这三人全选化学是对立事件
C. 乙同学在选物理的条件下选化学的概率是
D. 乙?丙两名同学都选物理的概率是
【答案】AD
【解析】A项:由于甲必选物理,故只需从剩下5门课中选两门即可,即C=10种选法,故A正确;
B项:甲?乙?丙三人至少一人选化学与全不选化学是对立事件,故B错误;
C项:由于乙同学选了物理,乙同学选化学的概率是=,故C错误;
D项:因为乙?丙两名同学各自选物理的概率为=,
所以乙?丙两名同学都选物理的概率是×=,故D正确,
故选AD.
12.已知函数f(x)=ln|x|-x+,给出下列四个结论,其中正确的是(??? )
A. 曲线y=f(x)在x=1处的切线方程为x+y+1=0
B. f(x)恰有2个零点
C. f(x)既有最大值,又有最小值
D. 若x1x2>0且f(x1)+f(x2)=0,则x1x2=1
【答案】BD
【解析】
对于A,当x>0时,
由于函数f(x)=lnx-x+,所以f'(x)=--1,
所以f(1)=0,f'(1)=--1=-1,
所以曲线y=f(x)在x=1处的切线方程为y=-1(x-1),即x+y-1=0,故A错误;
对于B?C,因为x>0时,f'(x)=<0,
所以f(x)在区间(0,+∞)上单调递减.
同理可求f(x)在区间(-∞,0)上单调递减,所以C错误;
又f(-1)=0,f(1)=0,
所以f(x)恰有2个零点,所以B正确;
对于D,若x1>0,x2>0,由f(x1)+f(x2)=0,
得f(x1)=-f(x2)=-(lnx2-x2+)=ln+-=f(),
即f(x1)=f().
因为f(x)在(0,+∞)上单调递减,所以x1=,即x1x2=1.
同理可证当x1<0,x2<0时,命题也成立.故D正确.
故选BD.
三、填空题:本大题共4小题,每小题5分,共20分.请把答案填写在答题卡相应位置上.
13.若曲线y=ax2在点(1,a)处的切线与直线x+2y-6=0垂直,则实数a的值为______.
【答案】1
【解析】由y=ax2,得y'=2ax,y'|x=1=2a,
∵曲线y=ax2在点(1,a)处的切线与直线x+2y-6=0垂直,
∴2a=2,a=1.
故答案为:1.
14.若z∈C,且|z+3+4i|≤2,则|z|的取值范围为____________.
【答案】[3,7]
【解析】设z=x+yi,(x,y∈R),
则|z+3+4i|=|(x+3)+(y+4)i|=≤2,
所以点z是复平面内以(-3,-4)为圆心,2为半径的圆上或圆内的点;
|z|=表示点z到原点的距离,|OC|==5,
OA=5-2=3为最小值,OB=5+2=7最大值,故取值范围为[3,7].
故答案为[3,7].
15.若对任意实数x,y都有(x-2y)5=a0(x+2y)5+a1(x+2y)4y+a2(x+2y)3y2+
a3(x+2y)2y3+a4(x+2y)y4+a5y5,则a0+a1+a2+a3+a4+a5的值为______.
【答案】-243
【解析】根据系数之间的关系,令x+2y=1,y=1,∴x=-1,y=1,∴a0+a1+a2+a3+a4+a5=(-3)5=-243,故答案为-243.
16.已知函数f(x)=(x+1)sinx+cosx,若对于任意的x1,x2∈[0,](x1≠x2),均有
|f(x1)-f(x2)|<a|e-e|成立,则实数a的取值范围为________.
【答案】[1,+∞)
【解析】由题意,函数f(x)=xsinx+sinx+cosx,
求导得f'(x)=xcosx+cosx=(x+1)cosx,
则由x∈[0,]可知f'(x)≥0恒成立,故f(x)在x∈[0,]单调递增,
不妨设x1<x2,则|f(x1)-f(x2)|=f(x2)-f(x1),|e-e|=e-e,
从而有f(x2)-f(x1)<a(e-e)恒成立,
即f(x2)-ae<f(x1)-ae恒成立,
设g(x)=f(x)-aex,则g(x)在x∈[0,]单调递减,
所以g'(x)=(x+1)cosx-aex≤0恒成立,
整理得a≥恒成立,设h(x)=,求导得,h'(x)=≤0,,所以h(x)=单调递减,则要a≥()max恒成立,
只要a≥h(0)=1,故答案为[1,+∞).
四、解答题:本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出必要的文字说明,证明过程或演算步骤.
17.(本小题共10分)
为了普及安全教育,某市组织了一次学生安全知识竞赛,规定每队3人,每人回答一个问题,答对得1分,答错得0分.在竞赛中,甲?乙两个中学代表队狭路相逢,假设甲队每人回答问题正确的概率均为,乙队每人回答问题正确的概率分别为,,,且两队各人回答问题正确与否相互之间没有影响.
(1)分别求甲队总得分为3分与1分的概率;
(2)求乙队总得分为1分的概率.
【答案】(1)记“甲队总得分为3分”为事件A,记“甲队总得分为1分”为事件B.
甲队得3分,即三人都回答正确,其概率P(A)=××=. 3分
甲队得1分,即三人中只有1人答对,其余两人都答错,
其概率P(B)=×(1-)×(1-)+(1-)××(1-)+(1-)×(1-)×
=C××()2=. 6分
答:甲队总得分为3分的概率为,甲队总得分为1分的概率为.
(2)记“乙队总得分为1分”为事件C.
事件C即乙队3人中只有1人答对,其余2人答错,
则P(C)=×(1-)×(1-)+(1-)××(1-)+(1-)×(1-)×=. 10分
答:乙队总得分为1分的概率为.
18.(本小题共12分)
若(+)n的二项式展开式中前三项的系数和为163,求:
(1)该二项式展开式中所有的有理项;
(2)该二项式展开式中系数最大的项.
【答案】展开式前三项的系数为1,2C,4C.
由题意得1+2C+4C=163,整理得n2=81,所以n=9. 2分
(1)设展开式中的有理项为Tk+1,
由Tk+1=C()9-k()k=2kCx,
又∵0≤k≤9,∴k=2或6.
故有理项为T3=22C·x=144x3,T7=26·C·x=5376. 6分
(2)设展开式中Tk+1项的系数最大,
则
∴≤k≤,又∵k∈N,∴k=6,
故展开式中系数最大的项为T7=5376. 12分
19.(本小题共12分)
403415518415如图,在正四棱柱ABCD-A1 B1 C1 D1中,AA1=2,AB=1,点N是BC的中点,点M在线段CC1上(不含端点).设二面角A1-DN-M的大小为θ.
(1)当θ=90°时,求AM的长;
(2)当cos θ=时,求CM的长.
解:建立如图所示的空间直角坐标系D-xyz.设CM=t(0
所以=(,1,0),=(0,1,t),=(1,0,2).
设平面DMN的法向量为n1=(x1,y1,z1),则n1·=0,n1·=0.
即x1+2 y1=0,y1+ tz1=0,令z1=1,则y1=- t,x1=2 t.
所以n1=(2t,-t,1)是平面DMN的一个法向量. 3分
设平面A1 DN的法向量为n2=(x2,y2,z2),则
n2·=0,n2·=0.即x2+2 z2=0,x2+2 y2=0.
令z2=1,则x2=-2,y2=1.
所以n2=(-2,1,1)是平面A1 DN的一个法向量. 6分
从而n1·n2=-5 t+1.
(1)因为θ=90°,所以n1·n2=-5 t+1=0,解得t=.从而M(0,1,).
所以AM==. 8分
(2)因为|n1|=,|n2|=,
所以cos<n1,n2>==.
因为<n1,n2>=θ或π-θ,所以||=,解得t=0或t=.
所以t=,从而CM的长为. 12分
20.(本小题共12分)
241490573025高三年级某班50名学生期中考试数学成绩的频率分布直方图如图所示,成绩分组区间为:[80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150].其中a,b,c成等差数列且c=2a.
物理成绩统计如表.(说明:数学满分150分,物理满分100分)
分组
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
频数
6
9
20
10
5
(1)根据频率分布直方图,求出实数a,b,c的值以及数学成绩为“优”的人数;
(2)若数学成绩不低于140分等第为“优”,物理成绩不低于90分等第为“优”,已知本班中至少有一个“优”同学总数为6人,从该6人中随机抽取3人,记X为抽到两个“优”的学生人数,求X的分布列和数学期望.
【答案】解:(1)由于a+b+2c=0.052,a+c=2b,c=2a,
解得a=0.008,b=0.012,c=0.016,
数学成绩为“优”的人数:50×a×10=4(人) 4分
(2)数学成绩为“优”的同学有4人,物理成绩为“优”有5人,
因为至少有一个“优”的同学总数为6名同学,
故两科均为“优”的人数为3人, 6分
故X的取值为0?1?2?3.
P(X=0)==,P(x=1)==,
P(X=2)==,P(X=3)==.
X
0
1
2
3
P
?
?
?
E(X)=0×+1×+2×+3×=. 12分
21.(本小题共12分)
已知函数f(x)=2x3-ax2+1(a∈R).
(1)若a=3,求函数f(x)的单调区间;
(2)当a>0时,若函数f(x)在[-1,1]上的最大值和最小值的和为1,求实数a的值.
【答案】解:(1) f(x)=2x3-ax2+1,令f'(x)=6x2-2ax=2x(3x-a)=0,得x1=0,x2=1,
当a=3时,由f'(x)>0得x<0或x>1,即函数f(x)在(-∞,0)和(1,+∞)上单调递增,
由f'(x)<0得0<x<1,即函数f(x)在(0,1)上单调递减,
所以函数f(x)的单调递增区间为(-∞,0),(1,+∞),单调递减区间为(0,1). 4分
(2)当a>0时,函数f(x)在(-∞,0),(,+∞)上单调递增,在(0,)上单调递减,
此时函数f(x)有两个极值点,极大值为f(0)=1,极小值为f()=1-,
且f(-1)=-a-1,f(1)=3-a.
1若≥1,即a≥3时,f(x)max=f(0)=1,此时f(-1)<f(1),所以f(x)min=f(-1)=-a-1,
由f(x)max+f(x)min=1可得1+(-a-1)=1,即a=-1,不符合题意,舍去. 6分
2若0<<1,即0<a<3时,比较f(1)与f(0)的大小.
①若f(1)≥f(0),即3-a≥1,也即0<a≤2时,此时f(x)max=f(1)=3-a,
又因为f()=1->0,f(-1)=-a-1<0,所以f(x)min=f(-1)=-1-a,
由f(x)max+f(x)min=1可得(3-a)+(-1-a)=1,即a=,符合题意. 9分
②若f(1)<f(0),即3-a<1,即2<a<3时,此时f(x)max=f(0)=1.
又因为f()=1->0,f(-1)=-a-1<0,所以f(x)min=f(-1)=-1-a,
由f(x)max+f(x)min=1可得1+(-1-a)=1,即a=-1,不符合题意.
综上所述,所求实数a的值为. 12分
22.(本小题共12分)
已知函数f(x)=ax--lnx(a∈R).
(1)若f(x)是定义域上的增函数,求a的取值范围;
(2)当a>时,若函数f(x)有两个极值点x1,x2(x1<x2),求f(x1)-f(x2)的取值范围.
【答案】解:(1)f(x)的定义域为(0,+∞),f'(x)=a+-=,
∵f(x)在定义域内单调递增,
∴f'(x)≥0,即ax2-x+a≥0对x>0恒成立,
则a≥恒成立,∴a≥()max,
∵=≤=,
当且仅当x=1时上式取等,∴a≥,
所以,a的取值范围是[,+∞). 3分
(2)设方程f'(x)=0,即ax2-x+a=0的两根为x1,x2,且0<x1<x2,
由Δ=1-4a2>0且a>,得<a<,
∵x1x2=1,x1+x2=, 5分
∴2<x1+=<,∴<x1<1,
f(x1)-f(x2)=ax1--lnx1-(ax2--lnx2)
=ax1--lnx1-(-ax1+lnx1)=2(ax1--lnx1),
∵ax12-x1+a=0,
∴a=代入得f(x1)-f(x2)=2(-lnx1)=2(-lnx12), 8分
令x12=t,则<t<1,
令g(t)=-lnt,<t<1,g'(t)=<0,
∴g(t)在(,1)上递减,从而g(1)<g(t)<g(),
即0<g(t)<-+ln2,所以f(x1)-f(x2)的取值范围为(0,-+2ln2). 12分
同课章节目录
