辽宁省葫芦岛市普通高中2020-2021学年高一下学期期末学业质量监测数学试题 Word版含答案
文档属性
| 名称 | 辽宁省葫芦岛市普通高中2020-2021学年高一下学期期末学业质量监测数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 934.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 11:21:13 | ||
图片预览




文档简介
2021年葫芦岛市普通高中期末学业质量监测考试
高一数学
注意事项:
1.答题前,考生务必将自己的姓名、考号、考场号、座位号用2B铅笔涂在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题纸上.写在本试卷上无效.
3.考试结束,将本试卷和答题卡一并交回.
第Ⅰ卷(选择题,共60分)
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.角false的终边相同角是( )
A.false B.false C.false D.false
2.已知复数false,则false( )
A.false B.false C.false D.false
3.已知向量false,则false与false的夹角为( )
A.false B.false C.false D.false
4.已知角false的终边经过点false且false,则m等于( )
A.false B.3 C.false D.false
5.公元5世纪,古希腊哲学家特奥多鲁斯给出了奇妙的特奥多鲁斯螺旋如左图,螺旋的结构是由一系列直角三角形组成.右图称为特奥多鲁斯螺旋的加强图,第一个三角形是边长为1的等腰直角三角形,以后每个直角三角形都以上一个三角形的斜边为直角边,另一个直角边为1.将这些直角边在公共顶点处的角依次记为false,则与false最接近的角是( )
参考值:false
A.false B.false C.false D.false
6.已知false,则false( )
A.false B.false C.false D.false
7.鹳雀楼是我国著名古迹,位于今山西省永济市,传说常有鹳雀在此停留,故有此名.更有唐朝诗人王之涣在作品《登鹳雀楼》中写下千古名句“欲穷千里目,更上一层楼”.如图是复建的鹳雀楼的示意图,某位游客(身高忽略不计)从地面D点看楼的项点C的仰角为false,沿直线前进51.9米到达E点,此时看点A的仰角为false,若点B,E,D在一条直线上,false,则楼高false约为(false)( )
A.30米 B.60米 C.90米 D.103米
8.已知false的三边垂直平分线交于点O,且false,false,则false的值为( )
A.6 B.false C.8 D.10
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)
9.已知false为实数,则实数a的值可以是( )
A.1 B.false C.2 D.false
10.以下四个命题为真命题的是( )
A.两两相交且不过同一点的三条直线必在同一平面内
B.过空间中任意三点有且仅有一个平面
C.若空间两条直线不相交,则这两条直线平行
D.若直线false平面false,直线false平面false,则false
11.在false中,D在线段false上,且false,若false,则( )
A.false B.false的面积为false
C.false的周长为26 D.false为钝角三角形
12.已知函数false,则下列叙述正确的是( )
A.false的图像关于y轴对称 B.false的图像关于原点对称
C.false的图像关于直线false对称 D.false的最小值为2
第Ⅱ卷(非选择题,共90分)
三、填空题(本大题共4小题,每小题5分,共20分.)
13.已知false,则false________.
14.函数false的单调递增区间为________.
15.阿基米德和高斯、牛顿井列为世界三大数学家.阿基米德曾说过:“拾我一个支点,我就能撬起整个地球.”史料表明阿基米德在研究半正多面体方面做出过突出贡献,因此半正多面体也称“阿基米德多面体”.阿基米德多面体是由边数不全相同的正多边形围成的多面体,它体现了数学的对称美.将正方体沿交于一个顶点的三条棱的中点截去一个三棱锥,如此截去八个三棱锥,得到一个半多面体.该多面体有_______个面;若正方体的棱长为2,则该半正多面体的体积为________.(本小题第一空2分,第二空3分)
16.已知函数false的图像与函数false的图像交于A,B两点,则false(O为坐标原点)的面积为_______.
四、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步)
17.(本小题满分10分)
已知false为锐角,false.
(1)求false的值;
(2)求false的值.
18.(本小题满分12分)
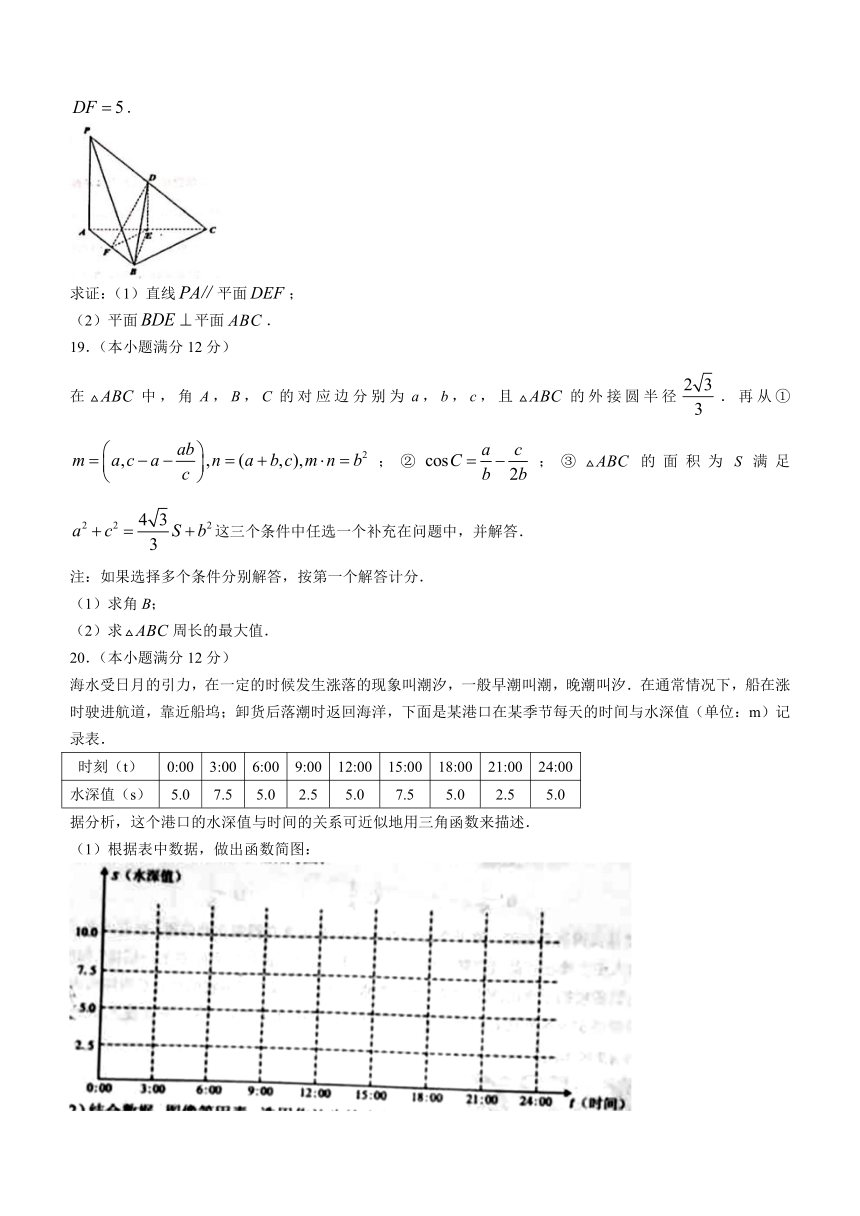
如图,在三棱锥false中,D,E,F分别为棱false的中点,已知false,false,false,false.
求证:(1)直线false平面false;
(2)平面false平面false.
19.(本小题满分12分)
在false中,角A,B,C的对应边分别为a,b,c,且false的外接圆半径false.再从①false;②false;③false的面积为S满足false这三个条件中任选一个补充在问题中,并解答.
注:如果选择多个条件分别解答,按第一个解答计分.
(1)求角B;
(2)求false周长的最大值.
20.(本小题满分12分)
海水受日月的引力,在一定的时候发生涨落的现象叫潮汐,一般早潮叫潮,晚潮叫汐.在通常情况下,船在涨时驶进航道,靠近船坞;卸货后落潮时返回海洋,下面是某港口在某季节每天的时间与水深值(单位:m)记录表.
时刻(t)
0:00
3:00
6:00
9:00
12:00
15:00
18:00
21:00
24:00
水深值(s)
5.0
7.5
5.0
2.5
5.0
7.5
5.0
2.5
5.0
据分析,这个港口的水深值与时间的关系可近似地用三角函数来描述.
(1)根据表中数据,做出函数简图:
(2)结合数据、图像等因素,选用你认为恰当的三角函数,求出解析式;并估计11:00时的水深值;
(3)一条货船的吃水深度(船底与水面的距离)为false,安全条例规定至少要有false的安全间隙(船底与海底的距离),该船何时能进入港口?在港口能停多久?
21.(本小题满分12分)
如图,直四棱柱false的底面是菱形,false.
(1)求二面角false的大小;
(2)求直线false与平面false所成角的大小.
22.(本小题满分12分)
已知函数false.
(1)若关于x的方程false在false上有解,求实数m的取值范围;
(2)记false的内角B满足false边上的高false为2,求false的最大值;
(3)函数false的图象纵坐标不变,横坐标伸长为原来的4倍,再把整个图象向左平移false个单位长度,再将函数图像向下平移1个单位得到false的图象.若false,false,问在false的图象上是否存在一点P,使得false.若存在,求出P点坐标;若不存在,说明理由.
2021年葫芦岛市普通高中期末学业质量监测考试
高一数学
参考答案及评分标准
一、单项选择题
AACB CDCC
二、多项选择题
9.AB 10.AD 11.BCD 12.AC
三、填空题
13.false 14.false 15.14;false 16.false
四、解答题
17.(本小题满分10分)
(1)由false,得false; 4
(2)由false为锐角,得false, 6
又false,∴false,
由false且false为锐角,得false. 8
则false
false. 10
18.(本小题满分12分)
(1)证明:因为D,E分别为棱false的中点,
所以false. 2
又因为false平面false,false平面false,
以直线false平面false. 4
(2)因为D,E,F分别为棱false的中点,false,
所以false. 6
又因为false,故false,
所以false,即false. 8
又false,所以false. 10
因为false,所以false平面false平面false,
所以false平面false.
又false平面false,所以平面false平面false. 12
19.(本小题满分12分)
(1)选①:由false得false 2
整理:false,false∴false
false 6
选②:由false得false 2
整理得:false,即false,∴false 4
false 6
选③:false,false 2
false 4
false 6
(2)由false,得false, 8
由余弦定理得:false,即false 10
∴false,当且仅当false时取等号,
从而周长false,
∴false周长的最大值为6. 12
20.(本小题满分12分)
(1)
(2)根据图象可考虑用函数false
刻画水深与时间的关系,从数据和图象可得:
false∴false 5
易知false,所以false,∴false. 6
∴false
当false时,false(米) 8
(3)货船的安全水深为false(米)
当false时可以进港,于是有false,整理得false
解得:false 10
又∵false
∴当false时,false;当false时,false
所以,货船可以在1时进港,5时出港或中午13时进港,17时出港,每次可以在港口停留4小时 12
21.(本小题满分12分)
(1)连false交false于M,连false.
∵四边形false为菱形,false分别为对角线,
∴false——① 1
由直四棱柱可知,false平面false,且false平面false
∴false——② 2
又∵false
∴false平面false
又∵false平面false 3
∴false,于是false是二面角false的平面角,而false是二面角false的补角. 4
∵false,false,∴false,false
在false中,false,∴false. 5
所以,二面角false的大小为false 6
(2)过C作false交false于N.
∵false
∴false与平面false所成角等于false与平面false所成的角 8
由(1)知,false平面false
又∵false平面false
∴平面false平面false
又∵面false面false,∴false面false
∴false面false
∴false就是所求的线面角 10
在false中,false
∴false与平面false所成角为false 12
22.(本小题满分12分)
(1)由false在false上有解可得;
false在false上有解. 2
设false
false
因为false,所以false,从而∴false
即false,所以false
(2)由false得false
∵false,∴false,∴false
在false中,false;在false中false 6
false
false
当false时,即false时,false有最大值false 8
另解:设false
在false中false
在false中false 6
∴false
其中false
所以,当false
即false时
false取大值false 8
(3)存在,理由如下:
由(1)知false,将false的图象(纵坐标不变)横坐标伸长为原来的4倍可得函数false再把整个图象向左平移false个单位长度得到false化简得:false,再将图像向下平移1个单位得false. 10
假设存在一点P,使得false,设点false,
false,false.
又false,所以false,false.
整理得:false.
易知,false
又因为false,
所以当且仅当false时,false和false同时等于false,
即false时,符合题意,故false上存在一点P,此时P点坐标为false 12
高一数学
注意事项:
1.答题前,考生务必将自己的姓名、考号、考场号、座位号用2B铅笔涂在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题纸上.写在本试卷上无效.
3.考试结束,将本试卷和答题卡一并交回.
第Ⅰ卷(选择题,共60分)
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.角false的终边相同角是( )
A.false B.false C.false D.false
2.已知复数false,则false( )
A.false B.false C.false D.false
3.已知向量false,则false与false的夹角为( )
A.false B.false C.false D.false
4.已知角false的终边经过点false且false,则m等于( )
A.false B.3 C.false D.false
5.公元5世纪,古希腊哲学家特奥多鲁斯给出了奇妙的特奥多鲁斯螺旋如左图,螺旋的结构是由一系列直角三角形组成.右图称为特奥多鲁斯螺旋的加强图,第一个三角形是边长为1的等腰直角三角形,以后每个直角三角形都以上一个三角形的斜边为直角边,另一个直角边为1.将这些直角边在公共顶点处的角依次记为false,则与false最接近的角是( )
参考值:false
A.false B.false C.false D.false
6.已知false,则false( )
A.false B.false C.false D.false
7.鹳雀楼是我国著名古迹,位于今山西省永济市,传说常有鹳雀在此停留,故有此名.更有唐朝诗人王之涣在作品《登鹳雀楼》中写下千古名句“欲穷千里目,更上一层楼”.如图是复建的鹳雀楼的示意图,某位游客(身高忽略不计)从地面D点看楼的项点C的仰角为false,沿直线前进51.9米到达E点,此时看点A的仰角为false,若点B,E,D在一条直线上,false,则楼高false约为(false)( )
A.30米 B.60米 C.90米 D.103米
8.已知false的三边垂直平分线交于点O,且false,false,则false的值为( )
A.6 B.false C.8 D.10
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)
9.已知false为实数,则实数a的值可以是( )
A.1 B.false C.2 D.false
10.以下四个命题为真命题的是( )
A.两两相交且不过同一点的三条直线必在同一平面内
B.过空间中任意三点有且仅有一个平面
C.若空间两条直线不相交,则这两条直线平行
D.若直线false平面false,直线false平面false,则false
11.在false中,D在线段false上,且false,若false,则( )
A.false B.false的面积为false
C.false的周长为26 D.false为钝角三角形
12.已知函数false,则下列叙述正确的是( )
A.false的图像关于y轴对称 B.false的图像关于原点对称
C.false的图像关于直线false对称 D.false的最小值为2
第Ⅱ卷(非选择题,共90分)
三、填空题(本大题共4小题,每小题5分,共20分.)
13.已知false,则false________.
14.函数false的单调递增区间为________.
15.阿基米德和高斯、牛顿井列为世界三大数学家.阿基米德曾说过:“拾我一个支点,我就能撬起整个地球.”史料表明阿基米德在研究半正多面体方面做出过突出贡献,因此半正多面体也称“阿基米德多面体”.阿基米德多面体是由边数不全相同的正多边形围成的多面体,它体现了数学的对称美.将正方体沿交于一个顶点的三条棱的中点截去一个三棱锥,如此截去八个三棱锥,得到一个半多面体.该多面体有_______个面;若正方体的棱长为2,则该半正多面体的体积为________.(本小题第一空2分,第二空3分)
16.已知函数false的图像与函数false的图像交于A,B两点,则false(O为坐标原点)的面积为_______.
四、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步)
17.(本小题满分10分)
已知false为锐角,false.
(1)求false的值;
(2)求false的值.
18.(本小题满分12分)
如图,在三棱锥false中,D,E,F分别为棱false的中点,已知false,false,false,false.
求证:(1)直线false平面false;
(2)平面false平面false.
19.(本小题满分12分)
在false中,角A,B,C的对应边分别为a,b,c,且false的外接圆半径false.再从①false;②false;③false的面积为S满足false这三个条件中任选一个补充在问题中,并解答.
注:如果选择多个条件分别解答,按第一个解答计分.
(1)求角B;
(2)求false周长的最大值.
20.(本小题满分12分)
海水受日月的引力,在一定的时候发生涨落的现象叫潮汐,一般早潮叫潮,晚潮叫汐.在通常情况下,船在涨时驶进航道,靠近船坞;卸货后落潮时返回海洋,下面是某港口在某季节每天的时间与水深值(单位:m)记录表.
时刻(t)
0:00
3:00
6:00
9:00
12:00
15:00
18:00
21:00
24:00
水深值(s)
5.0
7.5
5.0
2.5
5.0
7.5
5.0
2.5
5.0
据分析,这个港口的水深值与时间的关系可近似地用三角函数来描述.
(1)根据表中数据,做出函数简图:
(2)结合数据、图像等因素,选用你认为恰当的三角函数,求出解析式;并估计11:00时的水深值;
(3)一条货船的吃水深度(船底与水面的距离)为false,安全条例规定至少要有false的安全间隙(船底与海底的距离),该船何时能进入港口?在港口能停多久?
21.(本小题满分12分)
如图,直四棱柱false的底面是菱形,false.
(1)求二面角false的大小;
(2)求直线false与平面false所成角的大小.
22.(本小题满分12分)
已知函数false.
(1)若关于x的方程false在false上有解,求实数m的取值范围;
(2)记false的内角B满足false边上的高false为2,求false的最大值;
(3)函数false的图象纵坐标不变,横坐标伸长为原来的4倍,再把整个图象向左平移false个单位长度,再将函数图像向下平移1个单位得到false的图象.若false,false,问在false的图象上是否存在一点P,使得false.若存在,求出P点坐标;若不存在,说明理由.
2021年葫芦岛市普通高中期末学业质量监测考试
高一数学
参考答案及评分标准
一、单项选择题
AACB CDCC
二、多项选择题
9.AB 10.AD 11.BCD 12.AC
三、填空题
13.false 14.false 15.14;false 16.false
四、解答题
17.(本小题满分10分)
(1)由false,得false; 4
(2)由false为锐角,得false, 6
又false,∴false,
由false且false为锐角,得false. 8
则false
false. 10
18.(本小题满分12分)
(1)证明:因为D,E分别为棱false的中点,
所以false. 2
又因为false平面false,false平面false,
以直线false平面false. 4
(2)因为D,E,F分别为棱false的中点,false,
所以false. 6
又因为false,故false,
所以false,即false. 8
又false,所以false. 10
因为false,所以false平面false平面false,
所以false平面false.
又false平面false,所以平面false平面false. 12
19.(本小题满分12分)
(1)选①:由false得false 2
整理:false,false∴false
false 6
选②:由false得false 2
整理得:false,即false,∴false 4
false 6
选③:false,false 2
false 4
false 6
(2)由false,得false, 8
由余弦定理得:false,即false 10
∴false,当且仅当false时取等号,
从而周长false,
∴false周长的最大值为6. 12
20.(本小题满分12分)
(1)
(2)根据图象可考虑用函数false
刻画水深与时间的关系,从数据和图象可得:
false∴false 5
易知false,所以false,∴false. 6
∴false
当false时,false(米) 8
(3)货船的安全水深为false(米)
当false时可以进港,于是有false,整理得false
解得:false 10
又∵false
∴当false时,false;当false时,false
所以,货船可以在1时进港,5时出港或中午13时进港,17时出港,每次可以在港口停留4小时 12
21.(本小题满分12分)
(1)连false交false于M,连false.
∵四边形false为菱形,false分别为对角线,
∴false——① 1
由直四棱柱可知,false平面false,且false平面false
∴false——② 2
又∵false
∴false平面false
又∵false平面false 3
∴false,于是false是二面角false的平面角,而false是二面角false的补角. 4
∵false,false,∴false,false
在false中,false,∴false. 5
所以,二面角false的大小为false 6
(2)过C作false交false于N.
∵false
∴false与平面false所成角等于false与平面false所成的角 8
由(1)知,false平面false
又∵false平面false
∴平面false平面false
又∵面false面false,∴false面false
∴false面false
∴false就是所求的线面角 10
在false中,false
∴false与平面false所成角为false 12
22.(本小题满分12分)
(1)由false在false上有解可得;
false在false上有解. 2
设false
false
因为false,所以false,从而∴false
即false,所以false
(2)由false得false
∵false,∴false,∴false
在false中,false;在false中false 6
false
false
当false时,即false时,false有最大值false 8
另解:设false
在false中false
在false中false 6
∴false
其中false
所以,当false
即false时
false取大值false 8
(3)存在,理由如下:
由(1)知false,将false的图象(纵坐标不变)横坐标伸长为原来的4倍可得函数false再把整个图象向左平移false个单位长度得到false化简得:false,再将图像向下平移1个单位得false. 10
假设存在一点P,使得false,设点false,
false,false.
又false,所以false,false.
整理得:false.
易知,false
又因为false,
所以当且仅当false时,false和false同时等于false,
即false时,符合题意,故false上存在一点P,此时P点坐标为false 12
同课章节目录
