15.2多边形

(共35张PPT)
从这些图形你能抽象出什么平面图形？
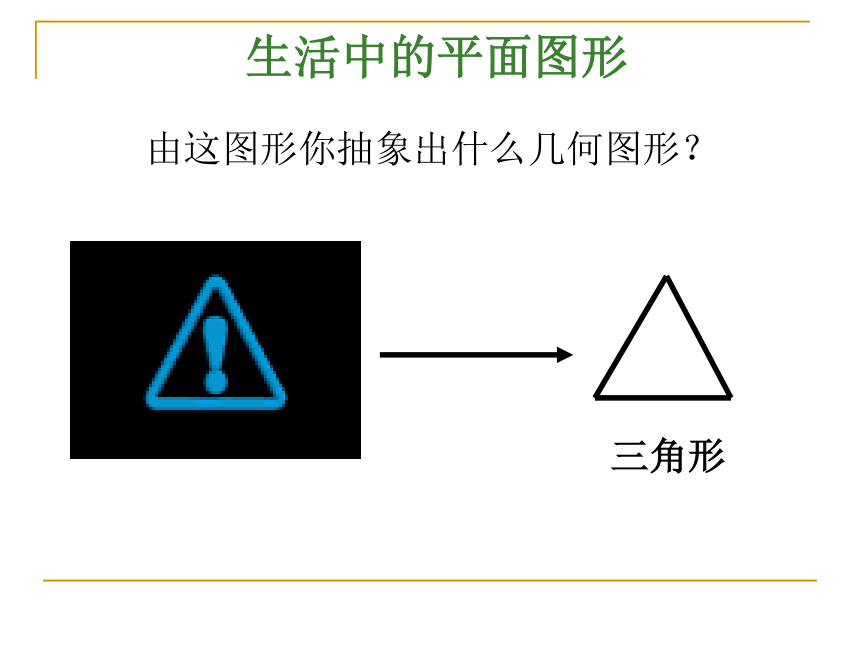
生活中的平面图形
由这图形你抽象出什么几何图形？
三角形
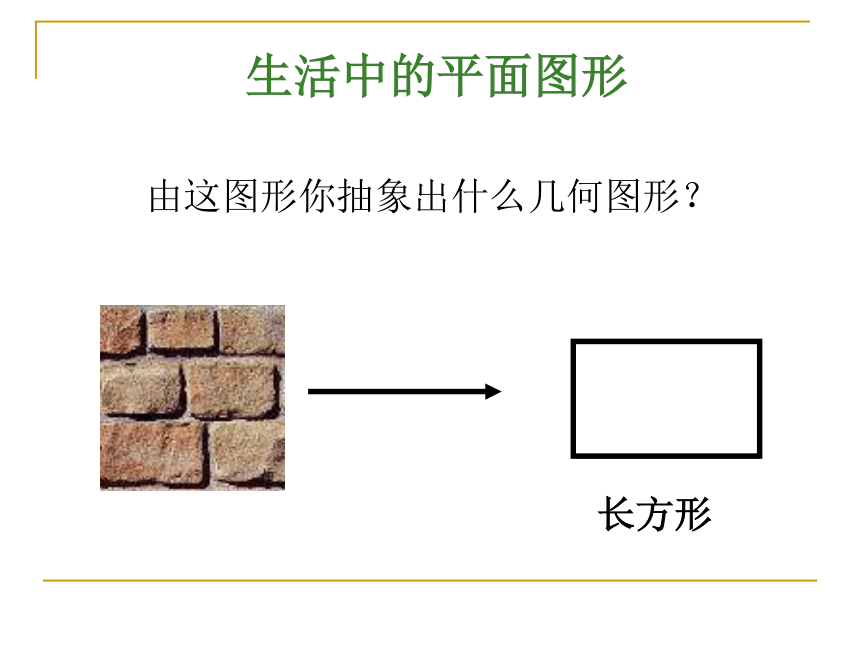
长方形
生活中的平面图形
由这图形你抽象出什么几何图形？
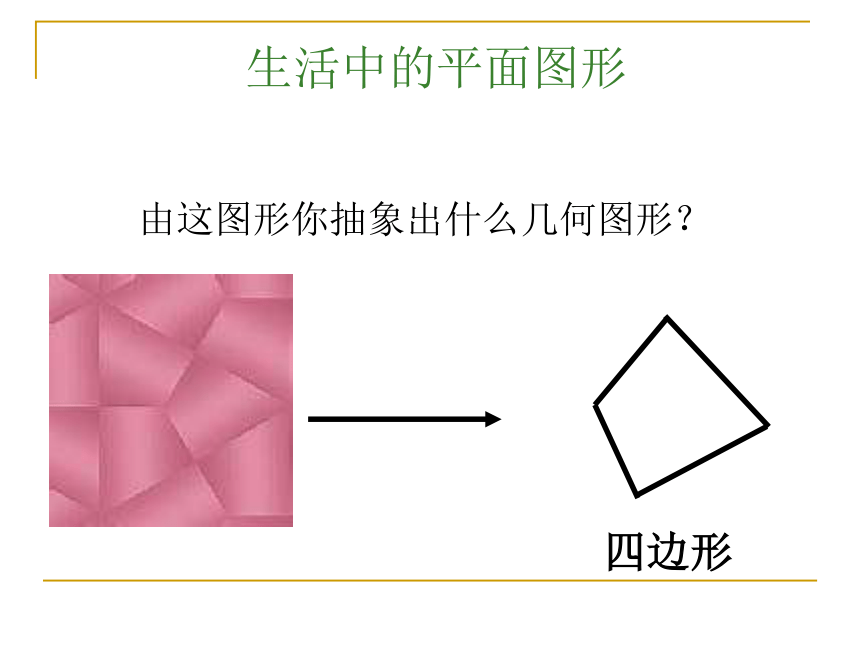
由这图形你抽象出什么几何图形？
四边形
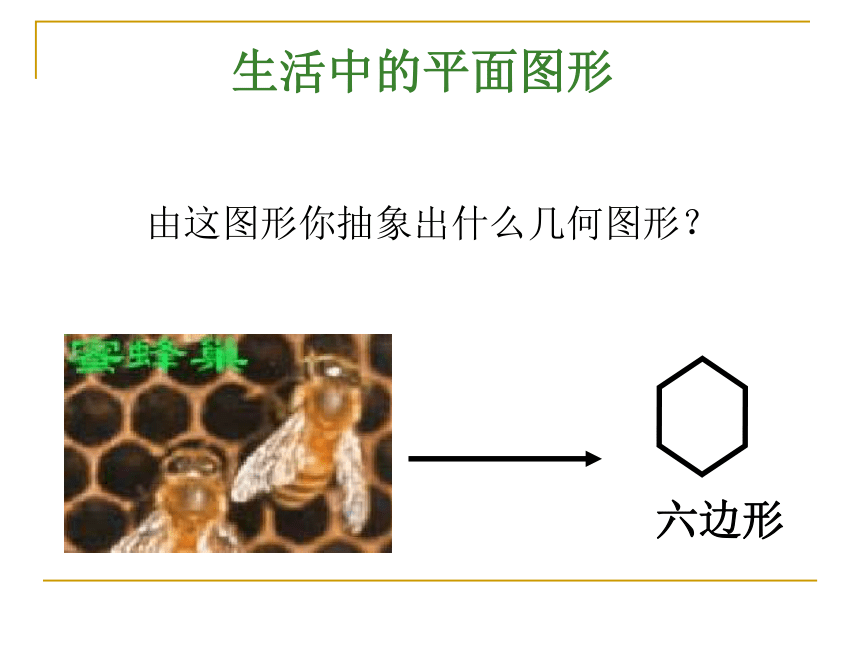
生活中的平面图形
六边形
生活中的平面图形
由这图形你抽象出什么几何图形？
三角形
长方形
六边形
四边形
八边形
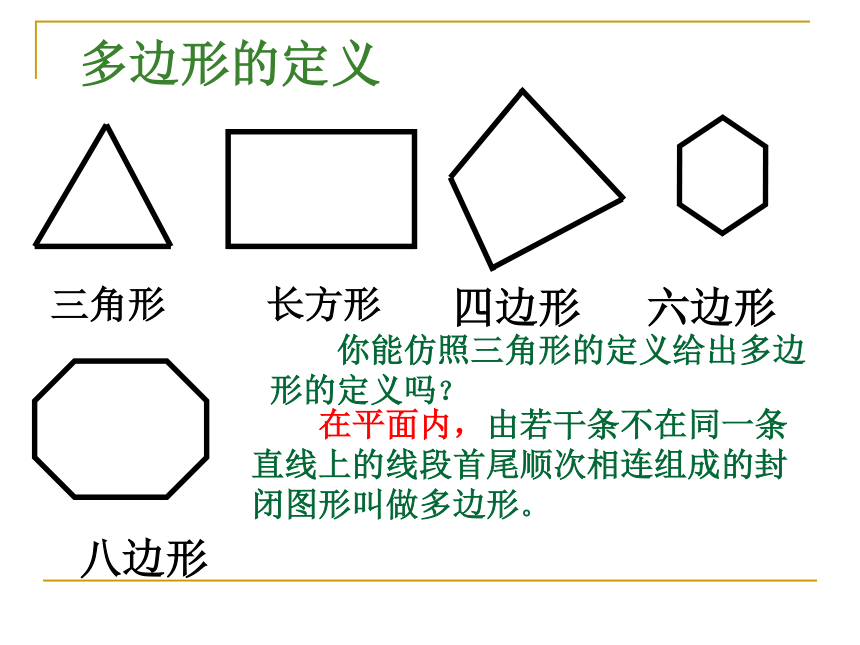
　　在平面内，由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
多边形的定义
　　你能仿照三角形的定义给出多边形的定义吗？
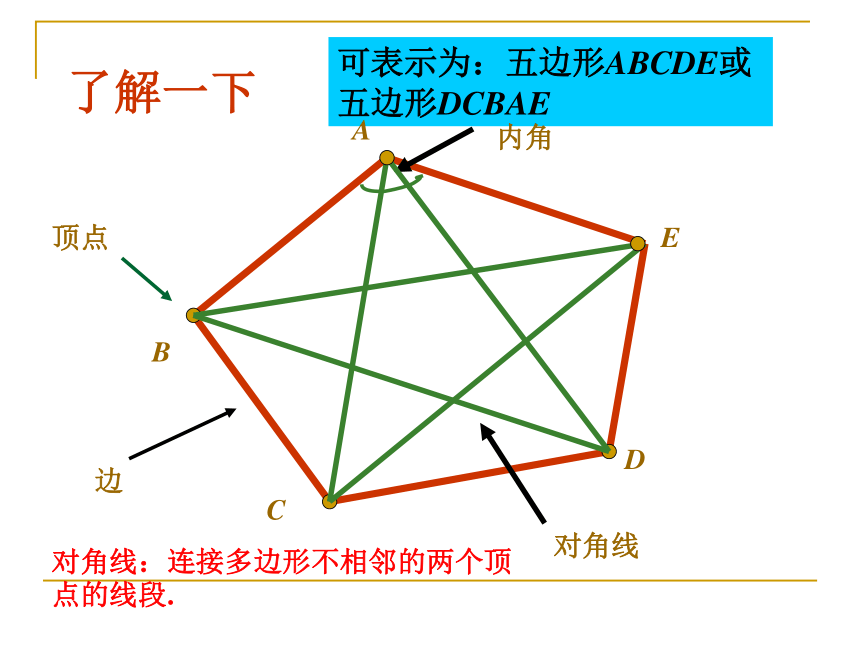
可表示为：五边形ABCDE或五边形DCBAE
了解一下
顶点
内角
边
对角线
对角线：连接多边形不相邻的两个顶点的线段.
A
B
C
D
E
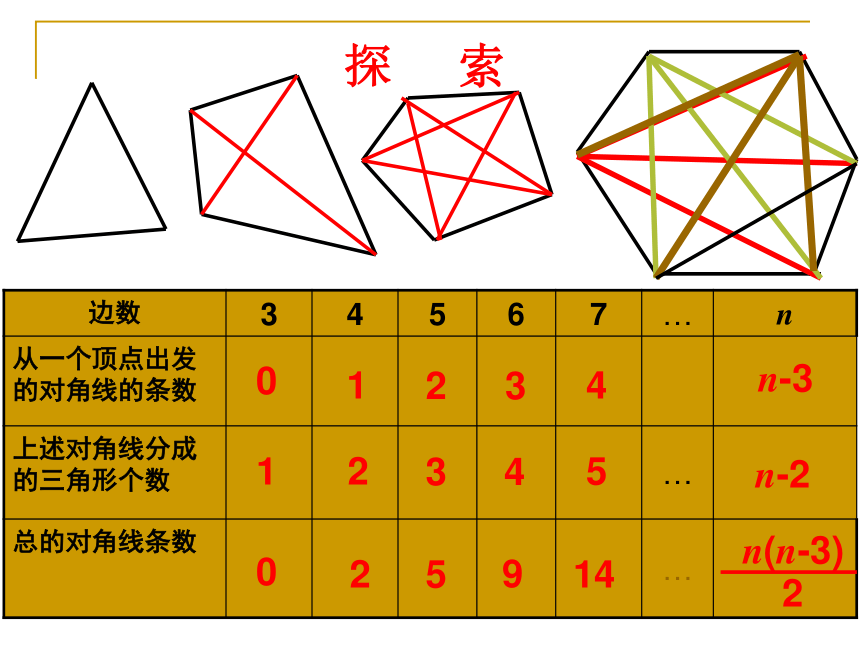
探 索
边数 3 4 5 6 7 … n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数 …
总的对角线条数 …
0
1
0
1
2
2
2
3
5
3
4
9
4
5
14
n-3
n-2
n(n-3)
2
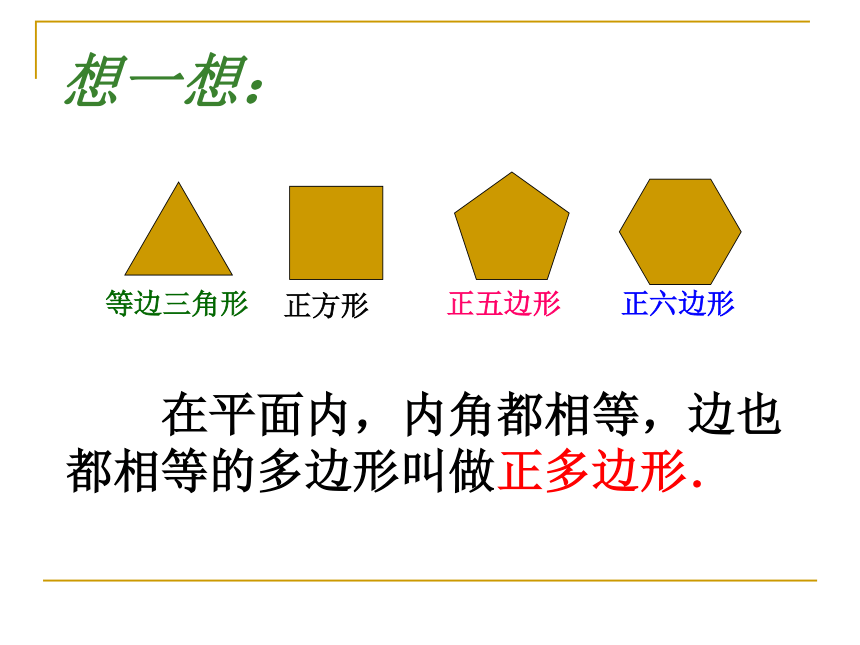
想一想：
　　在平面内，内角都相等，边也都相等的多边形叫做正多边形．
等边三角形
正方形
正五边形
正六边形
练一练：
1.小学学过的下列图形中不可能是正多边形的是( )
A.三角形 B.正方形 C.四边形 D.梯形
D
2.已知一个多边形有35条对角线，你能求出它的边数吗？
3.有一个家庭联谊会，参加的家庭全部是三口之家，在联谊会
期间，每个人都要和别的家庭的每个成员握一次手。
（1）若参加会议的人数为15，则一共要握手多少次？
（2）若一共握手170次，则参加会议的人数是多少？
B
A
C
D
E
探究1
5边形内角和=3×180°=540°
多边形 边数 分成三角形的个数 图形
内角和
计算规律
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
1
n-2
2
3
4
5
180°
360°
540°
720°
900°
(n－2) ·180°
(n－2) ·180°
5 ×180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
总结：n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n－2) ·180°
反思：我们是怎样求多边形内
角和的？
B
A
C
D
G
F
E
　　就是从多边形的一个顶点出发，把一个多边形分成几个三角形.
E
A
B
C
D
O
探究2
180°× 5 – 360°= 540°
180°× 5=900°？
五边形内角和540°？？
把一个五边形分成几个三角形，还有其他的分法吗？
A
B
C
D
E
F
180° × 4 – 180° = 540°
探究3
探究4
A
B
C
D
E
4 × 180°-180 °
O
=540°
十二边形的内角和是（ ）。
一个多边形当边数增加1时，它的内角和增加（ ）。
一个多边形的内角和是720 ，则此多边形共有（ ）个内角。
如果一个多边形的内角和是1440度，那么这是（ ）边形。
1800
180
六
十
例1 如图，在五边形的每个顶点处各取一个外角，这些外角的和叫做五边形的外角和．五边形的外角和等于多少？
6
E
B
C
D
1
2
3
4
5
A
1.任意一个外角和他相邻的内角有什么关系？
2.五个外角加上他们分别相邻的五个内角和是多少？
3.这五个平角和与五边形的内角和、外角和有什么关系？
例1 如图，在五边形的每个顶点处各取一个外角，这些外角的和叫做五边形的外角和．五边形的外角和等于多少？
5边形外角和
结论：五边形的外角和等于360°
-(5-2) × 180°
=360 °
6
E
B
C
D
1
2
3
4
5
A
=5个平角
-5边形内角和
=5×180°
探究在n边形的每个顶点处各取一个外角，这些外角的和叫做n边形的外角和．
n边形外角和=
结论：
n边形的外角和等于360°
-(n-2) × 180°
=360 °
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180 °
　　从多边形的一个顶点A点出发，沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向.在行程中所转的各个角的和，就是多边形的外角和.
　　由于在这个运动过程中走了一周，也就是说所转的各个角的和等于一个周角.
即：多边形的外角和等于360
练一练
练习1： 　　如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____.
12
n×30°=360°
n=12
n边形外角和=360 °
练习2：正五边形的每一个外角等于____， 每一个内角等于_____。
5x=360°
x=72°
72°
144°
解：设正五边形的每一个外角度数为x，由
多边形的外角和等于360度可得：
所以每一个内角度数为108 °
练习3. 已知一个多边形，它的内角和等 于外角和的2倍，求这个多边形的边数.
解： 设多边形的边数为n
∵它的内角和等于 (n-2) 180°，
多边形外角和等于360 ，
∴ (n-2) 180°=2× 360 。
解得: n=6
∴这个多边形的边数为6.
通过这节课的学习你有哪些收获？
1.n边形的内角和等于__________，九 边形的内角和等于___________.
2.如果一个多边形的内角和是1440度，那么这是____边形。
3.已知多边形的每个内角都等于150°，求这个多边形的边数？
4.一个多边形从一个顶点可引对角线3条，这个多边形内角和等于（ ）
A.360° B.540° C.720° D.900°
5.已知一个多边形，它的内角和等于外角和的2倍，求这个多边形的边数？
随堂练习
作　业
P１５６：习题15.2 A组的３、４、５题
这节课你学到了什么？