帮你归纳总结(三十四):立体几何中的折叠问题
文档属性
| 名称 | 帮你归纳总结(三十四):立体几何中的折叠问题 |  | |
| 格式 | zip | ||
| 文件大小 | 147.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-19 07:20:58 | ||
图片预览

文档简介
帮你归纳总结(三十四):立体几何中的折叠问题
对于折叠性问题,应确定图形在折叠前后的不变性质,如角的大小不变,线段长度不变,线线关系不变,再由面面垂直的判定定理进行推理证明;然后建立空间直角坐标系,利用向量的坐标和向量的数量积运算求解.
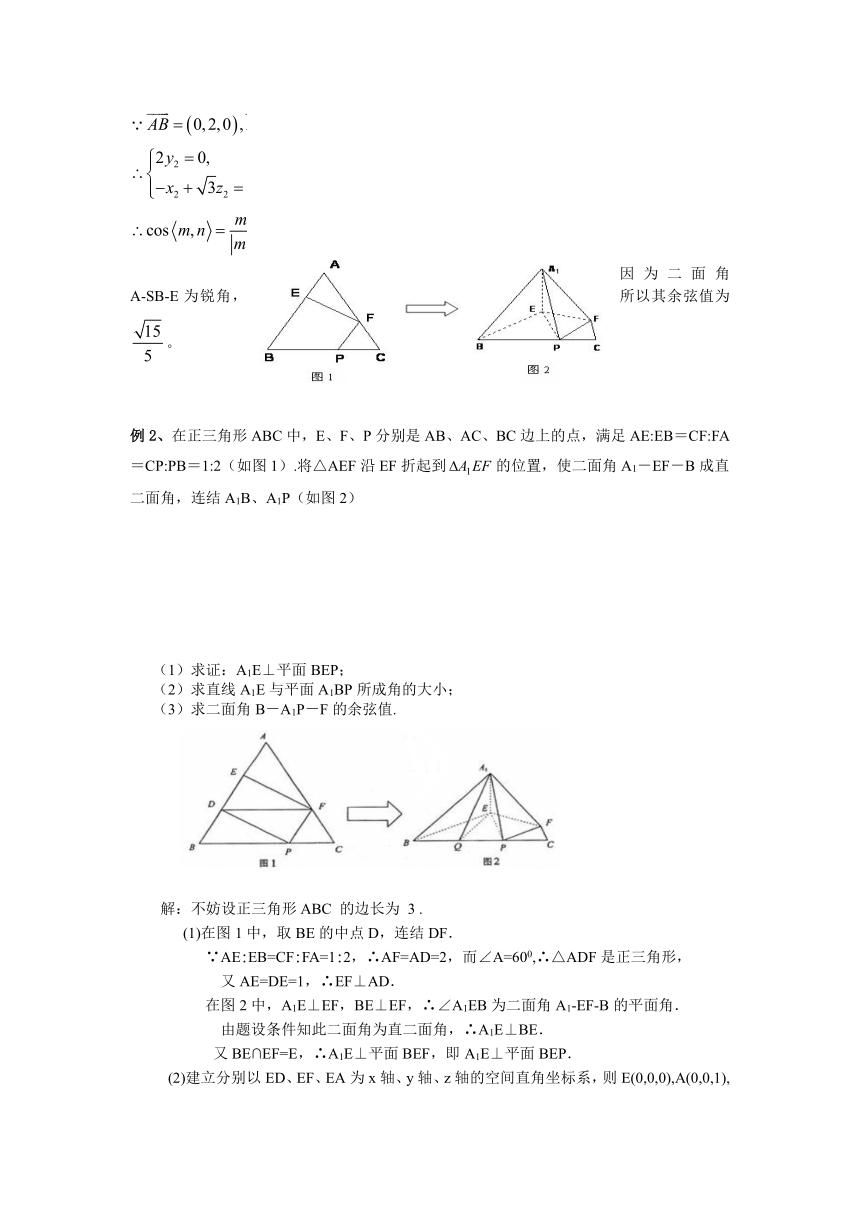
例1、如图1,在直角梯形ABCD中,AB//CD,AB=2, BC=1. 。如2,沿梯形的高 AE将其折成直二面角,使点D至点S的位置。
(1)求AE与SB所成角的余弦值;(2)求二面角A-SB-E的余弦值。
解:(1)有题设,为直二面角S-AE-C的平面角,于是EA、EC、ES两两互相垂直,
建立如图所示的空间直角坐标系,其中,
所以,AE与SB所成角的余弦值为。
(2)设为,面SBE的法向量,则,且
设为面SAB的法向量,则,且
因为二面角A-SB-E为锐角,所以其余弦值为。
例2、在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1).将△AEF沿EF折起到的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(1)求证:A1E⊥平面BEP;
(2)求直线A1E与平面A1BP所成角的大小;
(3)求二面角B-A1P-F的余弦值.
解:不妨设正三角形ABC 的边长为 3 .
(1)在图1中,取BE的中点D,连结DF.
∵AEEB=CFFA=12,∴AF=AD=2,而∠A=600,∴△ADF是正三角形,
又AE=DE=1,∴EF⊥AD.
在图2中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的平面角.
由题设条件知此二面角为直二面角,∴A1E⊥BE.
又BE∩EF=E,∴A1E⊥平面BEF,即A1E⊥平面BEP.
(2)建立分别以ED、EF、EA为x轴、y轴、z轴的空间直角坐标系,则E(0,0,0),A(0,0,1),
B(2,0,0),F(0, ,0), P (1, ,0),
则,.
设平面ABP的法向量为,
由平面ABP知,,即
令,得,.
,
, 所以直线A1E与平面A1BP所成的角为600.
(2) ,设平面AFP的法向量为.
由平面AFP知,,即
令,得,.
,
所以二面角B-A1P-F的余弦值是.
针对性练习:
如图,在△ABC中,∠ABC=,∠BAC,AD是BC上的高,沿AD把△ABD折起,
使∠BDC.(Ⅰ)证明:平面ADB⊥平面BDC;
(Ⅱ)设E为BC的中点,求与夹角的余弦值.
解:(Ⅰ)∵折起前AD是BC边上的高,
∴当△ABD折起后, AD⊥DC,AD⊥DB,
又DB∩DC=D,∴AD⊥平面BDC,
∵AD平面ABD,∴平面ABD⊥平面BDC.
(Ⅱ)由∠BDC及(1)知DA,DB,DC两两垂直,不妨设|DB|=1,以D为坐标原点, 以,,所在直线为轴建立如图
所示的空间直角坐标系,易得:
D(0,0,0),B(1,0,0),C(0,3,0),A(0,0,),E(,,0),
所以,,
∴
所以与夹角的余弦值是.
对于折叠性问题,应确定图形在折叠前后的不变性质,如角的大小不变,线段长度不变,线线关系不变,再由面面垂直的判定定理进行推理证明;然后建立空间直角坐标系,利用向量的坐标和向量的数量积运算求解.
例1、如图1,在直角梯形ABCD中,AB//CD,AB=2, BC=1. 。如2,沿梯形的高 AE将其折成直二面角,使点D至点S的位置。
(1)求AE与SB所成角的余弦值;(2)求二面角A-SB-E的余弦值。
解:(1)有题设,为直二面角S-AE-C的平面角,于是EA、EC、ES两两互相垂直,
建立如图所示的空间直角坐标系,其中,
所以,AE与SB所成角的余弦值为。
(2)设为,面SBE的法向量,则,且
设为面SAB的法向量,则,且
因为二面角A-SB-E为锐角,所以其余弦值为。
例2、在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1).将△AEF沿EF折起到的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(1)求证:A1E⊥平面BEP;
(2)求直线A1E与平面A1BP所成角的大小;
(3)求二面角B-A1P-F的余弦值.
解:不妨设正三角形ABC 的边长为 3 .
(1)在图1中,取BE的中点D,连结DF.
∵AEEB=CFFA=12,∴AF=AD=2,而∠A=600,∴△ADF是正三角形,
又AE=DE=1,∴EF⊥AD.
在图2中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的平面角.
由题设条件知此二面角为直二面角,∴A1E⊥BE.
又BE∩EF=E,∴A1E⊥平面BEF,即A1E⊥平面BEP.
(2)建立分别以ED、EF、EA为x轴、y轴、z轴的空间直角坐标系,则E(0,0,0),A(0,0,1),
B(2,0,0),F(0, ,0), P (1, ,0),
则,.
设平面ABP的法向量为,
由平面ABP知,,即
令,得,.
,
, 所以直线A1E与平面A1BP所成的角为600.
(2) ,设平面AFP的法向量为.
由平面AFP知,,即
令,得,.
,
所以二面角B-A1P-F的余弦值是.
针对性练习:
如图,在△ABC中,∠ABC=,∠BAC,AD是BC上的高,沿AD把△ABD折起,
使∠BDC.(Ⅰ)证明:平面ADB⊥平面BDC;
(Ⅱ)设E为BC的中点,求与夹角的余弦值.
解:(Ⅰ)∵折起前AD是BC边上的高,
∴当△ABD折起后, AD⊥DC,AD⊥DB,
又DB∩DC=D,∴AD⊥平面BDC,
∵AD平面ABD,∴平面ABD⊥平面BDC.
(Ⅱ)由∠BDC及(1)知DA,DB,DC两两垂直,不妨设|DB|=1,以D为坐标原点, 以,,所在直线为轴建立如图
所示的空间直角坐标系,易得:
D(0,0,0),B(1,0,0),C(0,3,0),A(0,0,),E(,,0),
所以,,
∴
所以与夹角的余弦值是.
同课章节目录
