2.4 解直角三角形 课件(共19张PPT)
文档属性
| 名称 | 2.4 解直角三角形 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 13:25:05 | ||
图片预览





文档简介
第二章 三角形的边角关系
4 解直角三角形
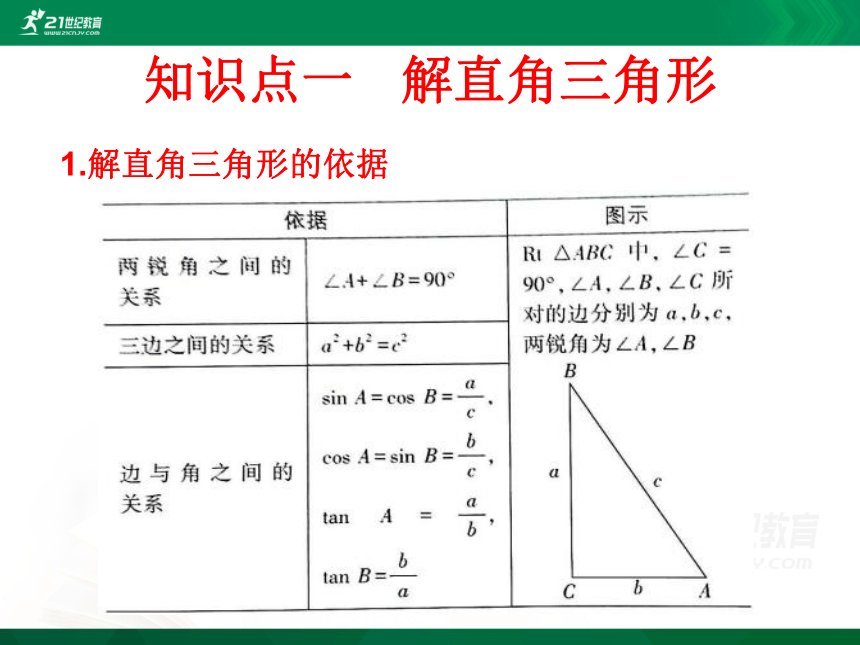
知识点一 解直角三角形
1.解直角三角形的依据
2. 解直角三角形的条件
在直角三角形的两锐角和三边这五个元素中,知道任意两个元素(其中至少一个是边),利用上面的三种关系,就可以求出其他元素.
3. 解直角三角形的定义
由直角三角形中已知的元素求出其他所有未知元素的过程,叫做解直角三角形.
2. 解直角三角形的条件
在直角三角形的两锐角和三边这五个元素中,知道任意两个元素(其中至少一个是边),利用上面的三种关系,就可以求出其他元素.
3. 解直角三角形的定义
由直角三角形中已知的元素求出其他所有未知元素的过程,叫做解直角三角形.
温馨提示 在直角三角形中,除直角外的五个元素,已知其中两个元素(至少有一条边),可求出其余的三个未知元素(知二求三).
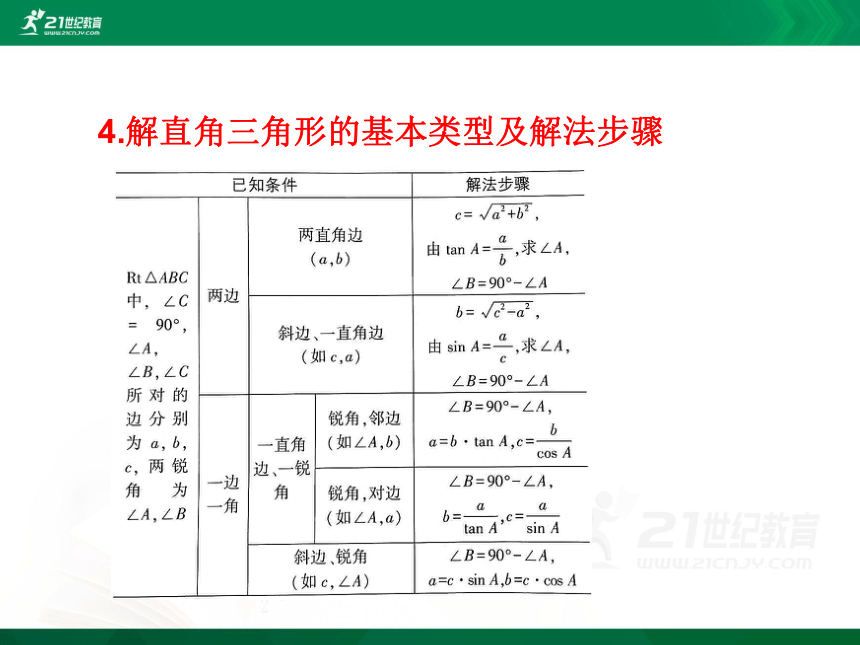
4.解直角三角形的基本类型及解法步骤
归纳总结
已知两边解直角三角形的步骤:
(1) 利用勾股定理求出第三边;
(2) 利用已知两边所对应的三角函数值求出一锐角;
(3) 利用两锐角互余求出另一角. 已知一边一角解直角三角形的步骤
(1) 利用两锐角互余求出另一角;
(2) 利用一边及一角所对应的三角函数值求出另两边.
归纳总结
已知两边解直角三角形的步骤:
(1) 利用勾股定理求出第三边;
(2) 利用已知两边所对应的三角函数值求出一锐角;
(3) 利用两锐角互余求出另一角. 已知一边一角解直角三角形的步骤
(1) 利用两锐角互余求出另一角;
(2) 利用一边及一角所对应的三角函数值求出另两边.
温馨提示 解直角三角形的思路可概括为“有斜(斜边)用弦(正弦、余弦),无斜用切(正切),宁乘勿除,取原避中”其含义是当已知中有斜边时,运用正弦或余弦,无斜边时,就用正切当所求元素可用乘法又可用除法时,通常用乘法, 不用除法;既可用原始数据又可用中间数据求解时,选用原始数据,忌用中间数据.
知识点二 解非直角三角形
若图形中没有直角三角形,往往需要添加辅助线构造直角三角形其一般思路:
(1)作垂线,构造直角三角形;
(2)构造含有特殊角的直角三角形;
(3)利用图形的性质构造,如等腰三角形顶角的平分线垂直于底边等.
方法归纳
添加辅助线构造直角三角形,特别是构造含有特殊角的直角三角形是解题的突破口.
经典例题
题型 解非直角三角形的有关计算
(2)如图所示,过点D作DE⊥AB于点E,过点B作BF⊥CD于点F,设DE=x(x>0).
由(1)知∠ABD=90°-∠EDB=90°-60°=30°.
∴∠DBC=∠ABC-∠ABD=105°-30°=75°.
则 , ,
.∴ .
方法归纳
在解题过程中,如果图中出现30°、45°、60°这些特殊的角,常考虑构造直角三角形,将这些特殊的角置于直角三角形中,以利用这些特殊角的三角函数值解决问题.
4 解直角三角形
知识点一 解直角三角形
1.解直角三角形的依据
2. 解直角三角形的条件
在直角三角形的两锐角和三边这五个元素中,知道任意两个元素(其中至少一个是边),利用上面的三种关系,就可以求出其他元素.
3. 解直角三角形的定义
由直角三角形中已知的元素求出其他所有未知元素的过程,叫做解直角三角形.
2. 解直角三角形的条件
在直角三角形的两锐角和三边这五个元素中,知道任意两个元素(其中至少一个是边),利用上面的三种关系,就可以求出其他元素.
3. 解直角三角形的定义
由直角三角形中已知的元素求出其他所有未知元素的过程,叫做解直角三角形.
温馨提示 在直角三角形中,除直角外的五个元素,已知其中两个元素(至少有一条边),可求出其余的三个未知元素(知二求三).
4.解直角三角形的基本类型及解法步骤
归纳总结
已知两边解直角三角形的步骤:
(1) 利用勾股定理求出第三边;
(2) 利用已知两边所对应的三角函数值求出一锐角;
(3) 利用两锐角互余求出另一角. 已知一边一角解直角三角形的步骤
(1) 利用两锐角互余求出另一角;
(2) 利用一边及一角所对应的三角函数值求出另两边.
归纳总结
已知两边解直角三角形的步骤:
(1) 利用勾股定理求出第三边;
(2) 利用已知两边所对应的三角函数值求出一锐角;
(3) 利用两锐角互余求出另一角. 已知一边一角解直角三角形的步骤
(1) 利用两锐角互余求出另一角;
(2) 利用一边及一角所对应的三角函数值求出另两边.
温馨提示 解直角三角形的思路可概括为“有斜(斜边)用弦(正弦、余弦),无斜用切(正切),宁乘勿除,取原避中”其含义是当已知中有斜边时,运用正弦或余弦,无斜边时,就用正切当所求元素可用乘法又可用除法时,通常用乘法, 不用除法;既可用原始数据又可用中间数据求解时,选用原始数据,忌用中间数据.
知识点二 解非直角三角形
若图形中没有直角三角形,往往需要添加辅助线构造直角三角形其一般思路:
(1)作垂线,构造直角三角形;
(2)构造含有特殊角的直角三角形;
(3)利用图形的性质构造,如等腰三角形顶角的平分线垂直于底边等.
方法归纳
添加辅助线构造直角三角形,特别是构造含有特殊角的直角三角形是解题的突破口.
经典例题
题型 解非直角三角形的有关计算
(2)如图所示,过点D作DE⊥AB于点E,过点B作BF⊥CD于点F,设DE=x(x>0).
由(1)知∠ABD=90°-∠EDB=90°-60°=30°.
∴∠DBC=∠ABC-∠ABD=105°-30°=75°.
则 , ,
.∴ .
方法归纳
在解题过程中,如果图中出现30°、45°、60°这些特殊的角,常考虑构造直角三角形,将这些特殊的角置于直角三角形中,以利用这些特殊角的三角函数值解决问题.
