2021-2022学年人教版数学八上同步检测附答案12.2 三角形全等的判定(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八上同步检测附答案12.2 三角形全等的判定(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 598.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 18:34:23 | ||
图片预览

文档简介
12.2
三角形全等的判定
一、选择题(共7小题;共35分)
1.
如图,,,要使
,则需增加的条件是
A.
B.
C.
D.
2.
在
的角平分线上有一点
,在
上有一点
,在
上有一点
,若
,则
与
A.
一定全等
B.
可能全等
C.
一定不全等
D.
无法确定
3.
如图,,
相交于点
,若
,,则图中的全等三角形有
A.
对
B.
对
C.
对
D.
对
4.
如图,
于点
,
于点
,且
,则
与
全等的理由是
A.
B.
C.
D.
5.
如果两个三角形全等,则不正确的是
A.
它们的最小角相等
B.
它们的对应外角相等
C.
它们是直角三角形
D.
它们的最长边相等
6.
如图,已知
,,,则判断
与
全等的依据是
A.
B.
C.
D.
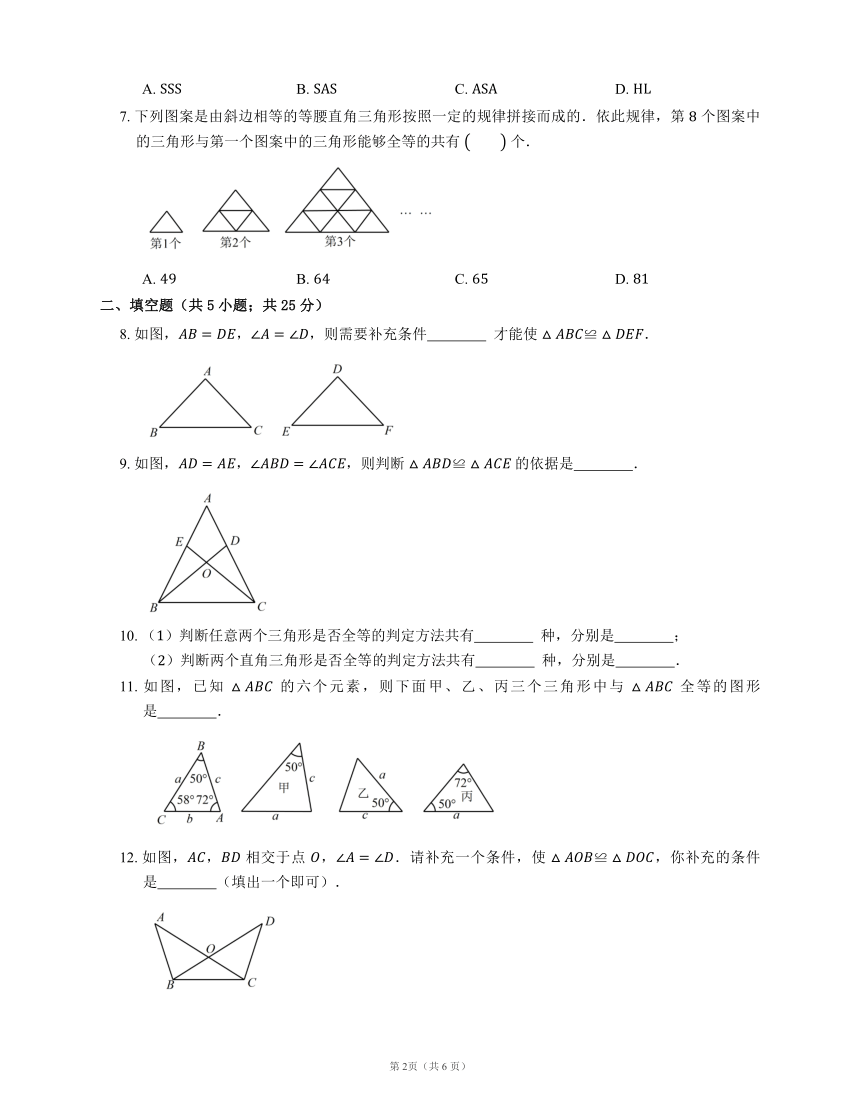
7.
下列图案是由斜边相等的等腰直角三角形按照一定的规律拼接而成的.依此规律,第
个图案中的三角形与第一个图案中的三角形能够全等的共有
个.
A.
B.
C.
D.
二、填空题(共5小题;共25分)
8.
如图,,,则需要补充条件
?
才能使
.
9.
如图,,,则判断
的依据是
?.
10.
()判断任意两个三角形是否全等的判定方法共有
?
种,分别是
?;
()判断两个直角三角形是否全等的判定方法共有
?
种,分别是
?.
11.
如图,已知
的六个元素,则下面甲、乙、丙三个三角形中与
全等的图形是
?.
12.
如图,,
相交于点
,.请补充一个条件,使
,你补充的条件是
?(填出一个即可).
三、解答题(共9小题;共90分)
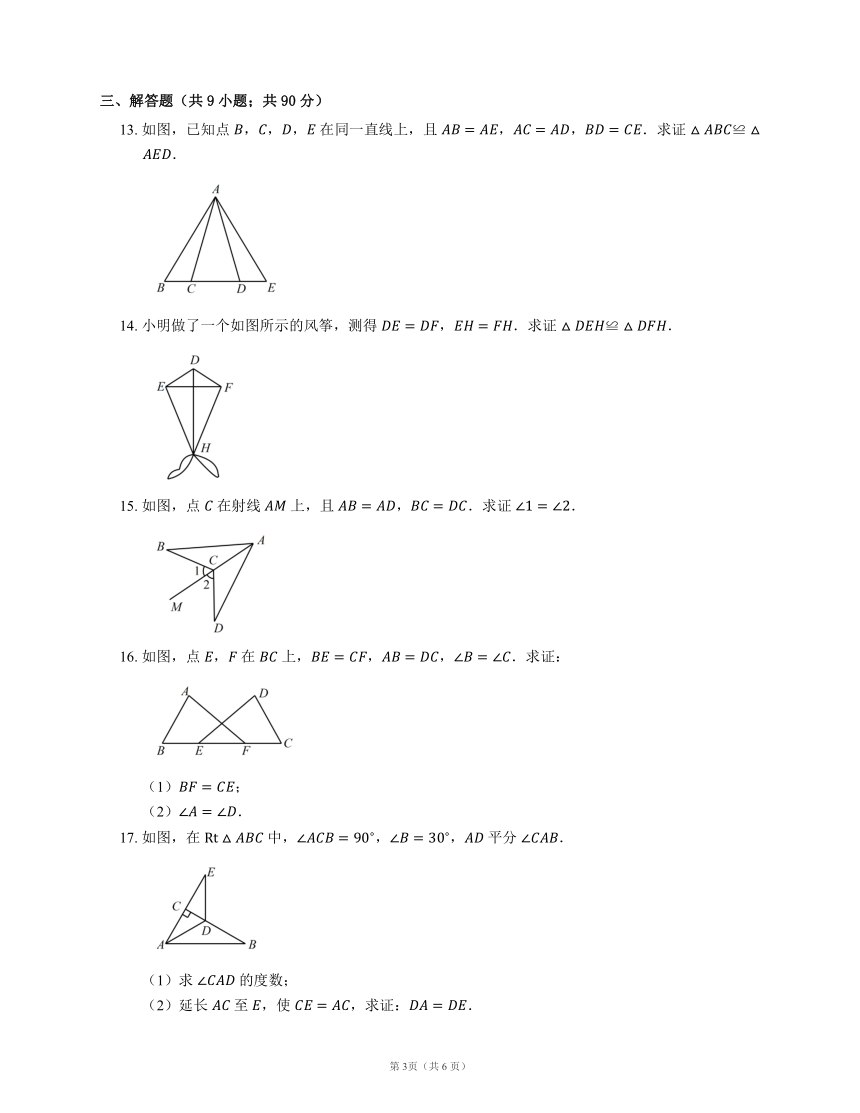
13.
如图,已知点
,,,
在同一直线上,且
,,.求证
.
14.
小明做了一个如图所示的风筝,测得
,.求证
.
15.
如图,点
在射线
上,且
,.求证
.
16.
如图,点
,
在
上,,,.求证:
(1);
(2).
17.
如图,在
中,,,
平分
.
(1)求
的度数;
(2)延长
至
,使
,求证:.
18.
如图,已知:在
和
中,点
,,,
在同一直线上,,,.求证:.
19.
如图,已知
,,.求证
.
20.
如图,
是
上一点,
交
于点
,,.求证
.
21.
如图,两根长度为
米的绳子,一端系在旗杆上,另一端分别固定在地面的两个木桩上,两个木桩离旗杆底部的距离相等吗?
请根据题目所给的信息填空,并完成证明过程.
已知:
?,
求证:
?.
证明:
答案
1.
B
2.
B
3.
C
4.
D
5.
C
6.
B
7.
B
【解析】第
个图案中,有
个三角形与第一个图案全等;
第
个图案中,有
个三角形与第一个图案中的三角形全等;根据上面的规律,可猜想第
个图案中有
个三角形与第一个图案中的三角形全等.
8.
(答案不唯一)
9.
10.
,,,,,,,,,,
11.
乙,丙
12.
或
或
13.
由
得
,
又因为
,,
所以
.
14.
因为
,,,
所以
.
15.
,,,
.
.
,
,
.
16.
(1)
,
.
.
??????(2)
,
.
在
和
中,
,,,
.
.
17.
(1)
在
中,,,
.
平分
,
,即
.
??????(2)
,且
,
,
.
在
与
中,
(),
.
18.
,
.
,
,即
.
在
和
中,
.
.
19.
,
,即
.
在
和
中,
.
20.
因为
,
所以
.
又因为
,,
所以
,
所以
.
21.
已知:
米,,垂足为
,
求证:.
,
又
在
和
中,,,
,
.
第6页(共6
页)
三角形全等的判定
一、选择题(共7小题;共35分)
1.
如图,,,要使
,则需增加的条件是
A.
B.
C.
D.
2.
在
的角平分线上有一点
,在
上有一点
,在
上有一点
,若
,则
与
A.
一定全等
B.
可能全等
C.
一定不全等
D.
无法确定
3.
如图,,
相交于点
,若
,,则图中的全等三角形有
A.
对
B.
对
C.
对
D.
对
4.
如图,
于点
,
于点
,且
,则
与
全等的理由是
A.
B.
C.
D.
5.
如果两个三角形全等,则不正确的是
A.
它们的最小角相等
B.
它们的对应外角相等
C.
它们是直角三角形
D.
它们的最长边相等
6.
如图,已知
,,,则判断
与
全等的依据是
A.
B.
C.
D.
7.
下列图案是由斜边相等的等腰直角三角形按照一定的规律拼接而成的.依此规律,第
个图案中的三角形与第一个图案中的三角形能够全等的共有
个.
A.
B.
C.
D.
二、填空题(共5小题;共25分)
8.
如图,,,则需要补充条件
?
才能使
.
9.
如图,,,则判断
的依据是
?.
10.
()判断任意两个三角形是否全等的判定方法共有
?
种,分别是
?;
()判断两个直角三角形是否全等的判定方法共有
?
种,分别是
?.
11.
如图,已知
的六个元素,则下面甲、乙、丙三个三角形中与
全等的图形是
?.
12.
如图,,
相交于点
,.请补充一个条件,使
,你补充的条件是
?(填出一个即可).
三、解答题(共9小题;共90分)
13.
如图,已知点
,,,
在同一直线上,且
,,.求证
.
14.
小明做了一个如图所示的风筝,测得
,.求证
.
15.
如图,点
在射线
上,且
,.求证
.
16.
如图,点
,
在
上,,,.求证:
(1);
(2).
17.
如图,在
中,,,
平分
.
(1)求
的度数;
(2)延长
至
,使
,求证:.
18.
如图,已知:在
和
中,点
,,,
在同一直线上,,,.求证:.
19.
如图,已知
,,.求证
.
20.
如图,
是
上一点,
交
于点
,,.求证
.
21.
如图,两根长度为
米的绳子,一端系在旗杆上,另一端分别固定在地面的两个木桩上,两个木桩离旗杆底部的距离相等吗?
请根据题目所给的信息填空,并完成证明过程.
已知:
?,
求证:
?.
证明:
答案
1.
B
2.
B
3.
C
4.
D
5.
C
6.
B
7.
B
【解析】第
个图案中,有
个三角形与第一个图案全等;
第
个图案中,有
个三角形与第一个图案中的三角形全等;根据上面的规律,可猜想第
个图案中有
个三角形与第一个图案中的三角形全等.
8.
(答案不唯一)
9.
10.
,,,,,,,,,,
11.
乙,丙
12.
或
或
13.
由
得
,
又因为
,,
所以
.
14.
因为
,,,
所以
.
15.
,,,
.
.
,
,
.
16.
(1)
,
.
.
??????(2)
,
.
在
和
中,
,,,
.
.
17.
(1)
在
中,,,
.
平分
,
,即
.
??????(2)
,且
,
,
.
在
与
中,
(),
.
18.
,
.
,
,即
.
在
和
中,
.
.
19.
,
,即
.
在
和
中,
.
20.
因为
,
所以
.
又因为
,,
所以
,
所以
.
21.
已知:
米,,垂足为
,
求证:.
,
又
在
和
中,,,
,
.
第6页(共6
页)
