课时2 命题及四种命题
图片预览





文档简介
(共16张PPT)
1.1命题及其关系(二)
1.1.3 四种命题的相互关系
回顾
交换原命题的条件和结论,所得的命题是________
同时否定原命题的条件和结论,所得的命题是________
交换原命题的条件和结论,并且同时否定,所得的命题是__________
逆命题。
否命题。
逆否命题。
三个概念
原命题,逆命题,否命题,逆否命题
四种命题形式:
原命题:
逆命题:
否命题:
逆否命题:
若 p, 则 q
若 q, 则 p
若┐p, 则┐q
若┐q, 则┐p
观察与思考
?
你能说出其中任意两个命题之间的关系吗
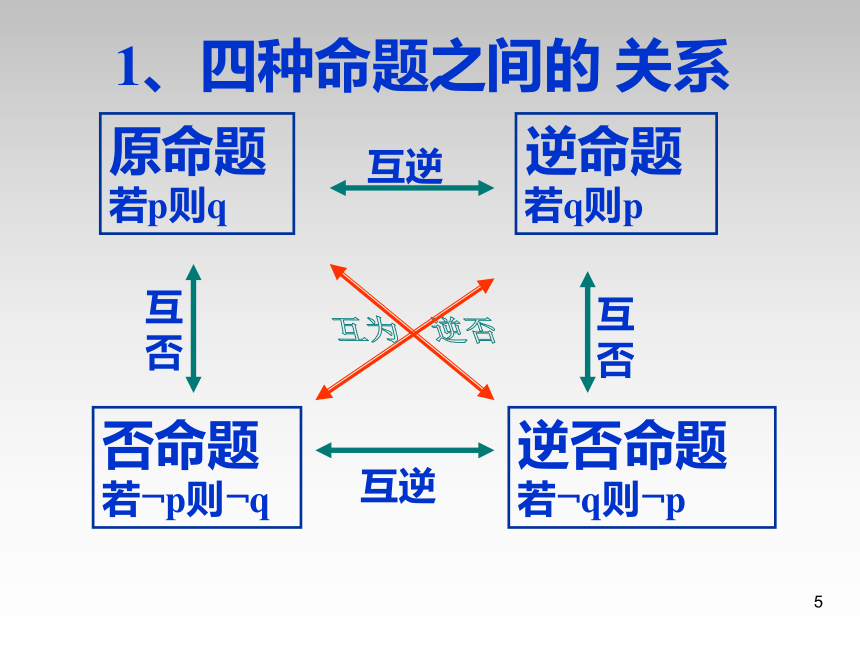
1、四种命题之间的 关系
原命题
若p则q
逆命题
若q则p
否命题
若﹁p则﹁q
逆否命题
若﹁q则﹁p
互逆
互否
互否
互逆
1)原命题:若a=0, 则ab=0。
逆命题:若ab=0, 则a=0。
否命题:若a≠ 0, 则ab≠0。
逆否命题:若ab≠0,则a≠0。
(真)
(假)
(假)
(真)
2.四种命题的真假
看下面的例子:
2) 原命题:若a > b, 则 ac2>bc2。
逆命题:若ac2>bc2,则a>b。
否命题:若a≤b,则ac2≤bc2。
逆否命题:若ac2≤bc2,则a≤b。
(假)
(真)
(真)
(假)
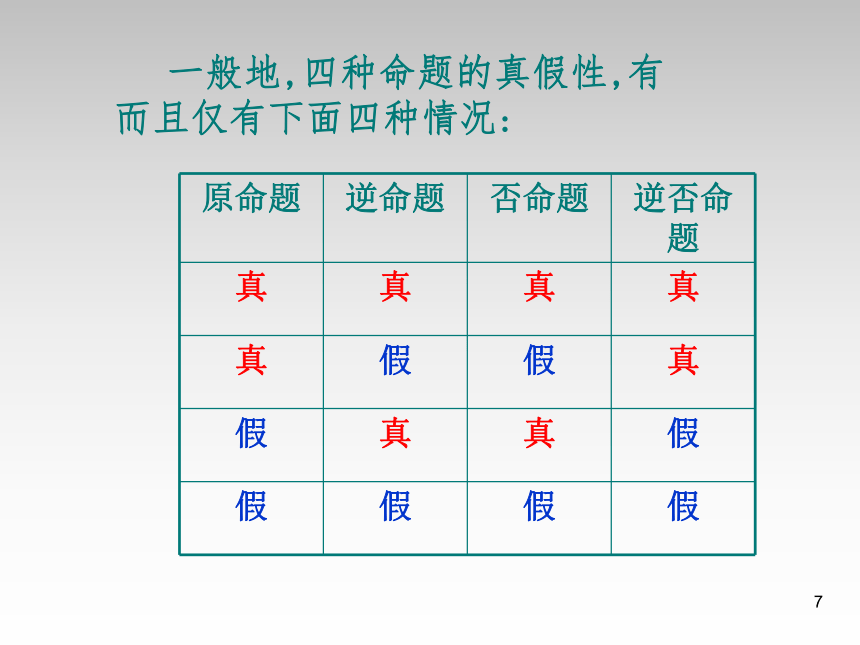
原命题 逆命题 否命题 逆否命题
真 真 真 真
真 假 假 真
假 真 真 假
假 假 假 假
一般地,四种命题的真假性,有而且仅有下面四种情况:
想一想?
(2) 若其逆命题为真,则其否命题一定为真。但其原命题、逆否命题不一定为真。
由以上三例及总结我们能发现什么?
即(1)原命题与逆否命题同真假。
逆命题与否命题同真假。
(1) 原命题为真,则其逆否命题一定为真。但其逆命题、否命题不一定为真。
总结:
即互为逆否的两个命题同真假!
练一练
1.判断下列说法是否正确。
1)一个命题的逆命题为真,它的逆否命题不一定为真;
(对)
2)一个命题的否命题为真,它的逆命题一定为真。
(对)
2.四种命题真假的个数可能为( )个。
答:0个、2个、4个。
例:原命题:若A∪B=A, 则A∩B=φ。
逆命题:若A∩B=φ,则A∪B=A。
否命题:若A∪B≠A,则A∩B≠φ。
逆否命题:若A∩B≠φ,则A∪B≠A。
(假)
(假)
(假)
(假)
3)一个命题的原命题为假,它的逆命题一定为假。
(错)
4)一个命题的逆否命题为假,它的否命题为假。
(错)
例题讲解
例题1:见P3之5题命题”若m>1/4,
则x2-x+1=0无实根”的否命题的等
价命题是
解:若mx2-x+1=0无实根,则m>1/4
见题6、判断二次函数y=ax2+bx+
c中,若b=a+c,则该二次函数不
存在有零点”,它的逆否命题是_,
并判断其真假.
小结:在判断四种命题的真假时,只需判断两种命题的
真假。因为逆命题与否命题真假等价,逆否命题与原命
题真假等价。
见P3:主人邀请张三、李四、王五三个人吃饭聊天,时间到了,只有张三和李四两人准时赶到,王五打来电话说:“临时有急事,不能来了。”主人听了随口说了句:“你看看,该来的没有来。”张三听了,脸色一沉,起来一声不吭地走了;主人愣了片刻,又道:“哎,不该走
的又走了。”李四听了大怒,拂袖而去。请你用逻辑学原理解释这两人离去的原因。
解:张三走的原因是:“该来的没有来”,逆否命题是--“来了的是不该来的!”从而导致张三认为自己是不该来的。
李四走的原因是“不该走的又走了”,其逆否命题是“没有走的是应该走的”,从而使李四觉得主人在赶自己走。
课堂小结
原命题
若p则q
逆命题
若q则p
否命题
若﹁ p则﹁ q
逆否命题
若﹁ q则﹁p
互为逆否 同真同假
互为逆否 同真同假
互逆命题 真假无关
互逆命题 真假无关
互否命题真假无关
互否命题真假无关
1.命题的四种形式之间的关系,提供了一个判断命题
真假的手段,由于互为逆否命题的两个命题是等价
命题,它们同真或同假,所以当一个命题不易判断
时,可以通过判断其逆否命题的真假来判断原命题
的真假
【★题1】写出下列命题的否定及否命题:
1、两组对边平行的四边形是平行四边形。
解:(否定形式:两组对边平行的四边形不是平行四边形;否命题:若一个四边形至少有一组对边不平行,则它不是平行四边形。
2、正整数1既不是质数也不是合数。
解:(否定形式:正整数1是质数或者是合数。否命题:若一个正整数不是1,则它是质数或者是合数。
3、命题“若a>b,则2a>2b-1”的否命题为_____(若a≤b, 则2a≤2b-1)
1.1命题及其关系(二)
1.1.3 四种命题的相互关系
回顾
交换原命题的条件和结论,所得的命题是________
同时否定原命题的条件和结论,所得的命题是________
交换原命题的条件和结论,并且同时否定,所得的命题是__________
逆命题。
否命题。
逆否命题。
三个概念
原命题,逆命题,否命题,逆否命题
四种命题形式:
原命题:
逆命题:
否命题:
逆否命题:
若 p, 则 q
若 q, 则 p
若┐p, 则┐q
若┐q, 则┐p
观察与思考
?
你能说出其中任意两个命题之间的关系吗
1、四种命题之间的 关系
原命题
若p则q
逆命题
若q则p
否命题
若﹁p则﹁q
逆否命题
若﹁q则﹁p
互逆
互否
互否
互逆
1)原命题:若a=0, 则ab=0。
逆命题:若ab=0, 则a=0。
否命题:若a≠ 0, 则ab≠0。
逆否命题:若ab≠0,则a≠0。
(真)
(假)
(假)
(真)
2.四种命题的真假
看下面的例子:
2) 原命题:若a > b, 则 ac2>bc2。
逆命题:若ac2>bc2,则a>b。
否命题:若a≤b,则ac2≤bc2。
逆否命题:若ac2≤bc2,则a≤b。
(假)
(真)
(真)
(假)
原命题 逆命题 否命题 逆否命题
真 真 真 真
真 假 假 真
假 真 真 假
假 假 假 假
一般地,四种命题的真假性,有而且仅有下面四种情况:
想一想?
(2) 若其逆命题为真,则其否命题一定为真。但其原命题、逆否命题不一定为真。
由以上三例及总结我们能发现什么?
即(1)原命题与逆否命题同真假。
逆命题与否命题同真假。
(1) 原命题为真,则其逆否命题一定为真。但其逆命题、否命题不一定为真。
总结:
即互为逆否的两个命题同真假!
练一练
1.判断下列说法是否正确。
1)一个命题的逆命题为真,它的逆否命题不一定为真;
(对)
2)一个命题的否命题为真,它的逆命题一定为真。
(对)
2.四种命题真假的个数可能为( )个。
答:0个、2个、4个。
例:原命题:若A∪B=A, 则A∩B=φ。
逆命题:若A∩B=φ,则A∪B=A。
否命题:若A∪B≠A,则A∩B≠φ。
逆否命题:若A∩B≠φ,则A∪B≠A。
(假)
(假)
(假)
(假)
3)一个命题的原命题为假,它的逆命题一定为假。
(错)
4)一个命题的逆否命题为假,它的否命题为假。
(错)
例题讲解
例题1:见P3之5题命题”若m>1/4,
则x2-x+1=0无实根”的否命题的等
价命题是
解:若mx2-x+1=0无实根,则m>1/4
见题6、判断二次函数y=ax2+bx+
c中,若b=a+c,则该二次函数不
存在有零点”,它的逆否命题是_,
并判断其真假.
小结:在判断四种命题的真假时,只需判断两种命题的
真假。因为逆命题与否命题真假等价,逆否命题与原命
题真假等价。
见P3:主人邀请张三、李四、王五三个人吃饭聊天,时间到了,只有张三和李四两人准时赶到,王五打来电话说:“临时有急事,不能来了。”主人听了随口说了句:“你看看,该来的没有来。”张三听了,脸色一沉,起来一声不吭地走了;主人愣了片刻,又道:“哎,不该走
的又走了。”李四听了大怒,拂袖而去。请你用逻辑学原理解释这两人离去的原因。
解:张三走的原因是:“该来的没有来”,逆否命题是--“来了的是不该来的!”从而导致张三认为自己是不该来的。
李四走的原因是“不该走的又走了”,其逆否命题是“没有走的是应该走的”,从而使李四觉得主人在赶自己走。
课堂小结
原命题
若p则q
逆命题
若q则p
否命题
若﹁ p则﹁ q
逆否命题
若﹁ q则﹁p
互为逆否 同真同假
互为逆否 同真同假
互逆命题 真假无关
互逆命题 真假无关
互否命题真假无关
互否命题真假无关
1.命题的四种形式之间的关系,提供了一个判断命题
真假的手段,由于互为逆否命题的两个命题是等价
命题,它们同真或同假,所以当一个命题不易判断
时,可以通过判断其逆否命题的真假来判断原命题
的真假
【★题1】写出下列命题的否定及否命题:
1、两组对边平行的四边形是平行四边形。
解:(否定形式:两组对边平行的四边形不是平行四边形;否命题:若一个四边形至少有一组对边不平行,则它不是平行四边形。
2、正整数1既不是质数也不是合数。
解:(否定形式:正整数1是质数或者是合数。否命题:若一个正整数不是1,则它是质数或者是合数。
3、命题“若a>b,则2a>2b-1”的否命题为_____(若a≤b, 则2a≤2b-1)
