课时3 充分，必要，充要条件

(共14张PPT)
1. 2.1—1.2.2
充分、必要、充要条件
知识点:
例:下列各题中, p是q的什么条件
p: b=0,
q: 函数f(x)=ax2+bx+c是偶函数;
2) p：整数a是６的倍数，
　q： 整数a是２和３的倍数.
充要条件
充要条件
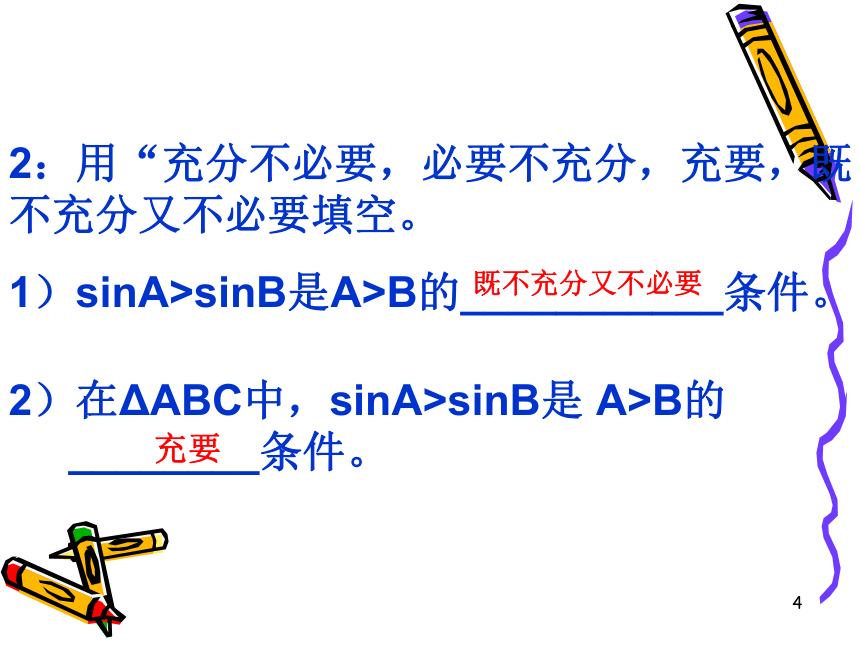
2：用“充分不必要，必要不充分，充要，既不充分又不必要填空。
1）sinA>sinB是A>B的___________条件。
既不充分又不必要
充要
2）在ΔABC中，sinA>sinB是 A>B的
________条件。
例: 判断下列问题中，p是q成立的什么条件？
（3） xy≠0 x≠0或y≠0
（2） |x-2|<4 -x2+4x+5>0
（1） x2>1 x<-1
p q
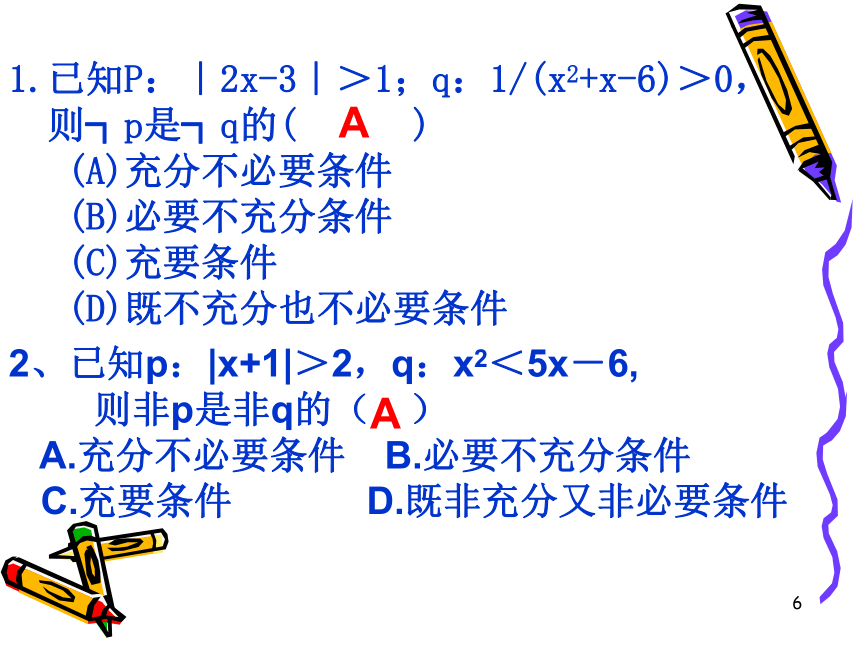
1.已知P：｜2x-3｜＞1；q：1/(x2+x-6)＞0，
则┐p是┐q的(　　　)
(A)充分不必要条件
(B)必要不充分条件
(C)充要条件
(D)既不充分也不必要条件
2、已知p：|x+1|＞2，q：x2＜5x－6,
则非p是非q的（　）
A.充分不必要条件　B.必要不充分条件　
C.充要条件　 D.既非充分又非必要条件
A
A
3、设集合M={x|x>2},N={x|x<3},
那么”x∈M或x∈N”是“x∈M∩N”的( )
A.充要条件 B必要不充分条件
C充分不必要 D不充分不必要
B
4、a∈R,|a|<3成立的一个必要不充分条件是( )
A.a<3 B.|a|<2 C.a2<9 D.0A
1.关于x的不等式：｜x｜+｜x-1｜＞m的
解集为R的充要条件是( )
(A)m＜0 (B)m≤0
(C)m＜1 (D)m≤1
C
1、已知p,q都是r的必要条件，
s是r的充分条件，q是s的充分条件，则
（1）s是q的什么条件？
（2）r是q的什么条件？
（3）P是q的什么条件？
充要条件
充要条件
必要条件
2.若A是B的必要而不充分条件，C是B的充要条件，D是C的充分而不必要条件，那么D是A的________
充分不必要条件
练习
3.已知p是q的必要而不充分条件，
那么┐p是┐q的_______________.
充分不必要条件
4：若┐A是┐B的充要条件,┐C是┐B的充　要条件,则A为C的（ ）条件
　　A.充要 B必要不充分
　　C充分不必要 D不充分不必要
Ａ
　1:求证：关于x的方程ax2+bx+c=0有一个
根为-1的充要条件是a-b+c=0.
【解题回顾】充要条件的证明一般分两步：
　　　　　证充分性即证A =>B，
　　　　　证必要性即证B=>A
三、小结
① 认清条件和结论。
② 考察p q和q p的真假。
① 可先简化命题。
③ 将命题转化为等价的逆否命题后再判断。
② 否定一个命题只要举出一个反例即可。
1、定义：
2、判别步骤：
3、判别技巧：
如果已知p q，则说p是q的充分条件， q是p的必要条件。