冀教版九年级数学上册《集训课堂 相似三角形的性质及应用》课件(共31张ppt)
文档属性
| 名称 | 冀教版九年级数学上册《集训课堂 相似三角形的性质及应用》课件(共31张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 00:00:00 | ||
图片预览




文档简介
集训课堂
相似三角形的性质及应用
JJ版九年级上
第二十五章 图形的相似
4
提示:点击 进入习题
答案显示
6
1
2
3
5
C
B
D
C
C
D
8
7
B
C
提示:点击 进入习题
答案显示
9
12
10
11
100厘米和40厘米
14
13
3
16
15
见习题
见习题
1:16
提示:点击 进入习题
答案显示
17
见习题
18
见习题
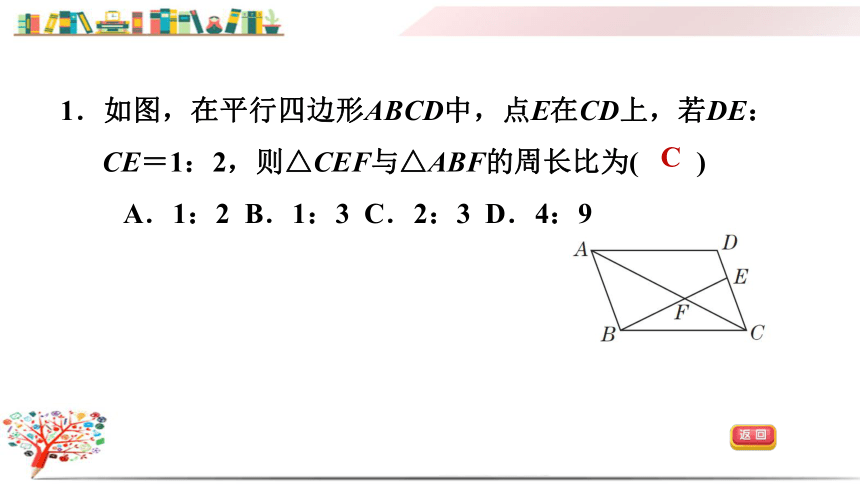
1.如图,在平行四边形ABCD中,点E在CD上,若DE:CE=1:2,则△CEF与△ABF的周长比为( )
A.1:2 B.1:3 C.2:3 D.4:9
C
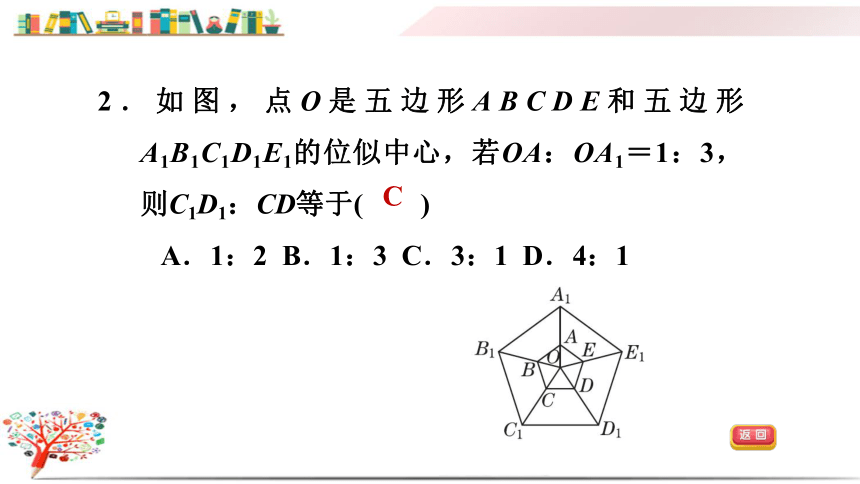
2.如图,点O是五边形ABCDE和五边形A1B1C1D1E1的位似中心,若OA:OA1=1:3,则C1D1:CD等于( )
A.1:2 B.1:3 C.3:1 D.4:1
C
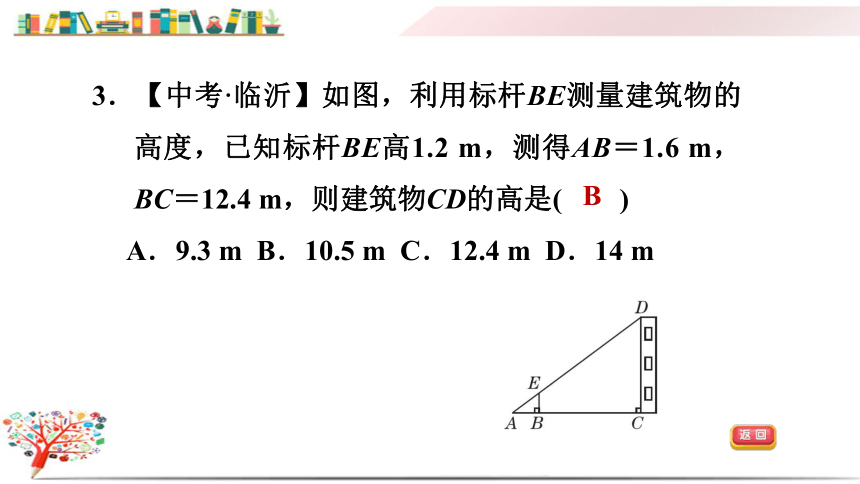
3.【中考·临沂】如图,利用标杆BE测量建筑物的高度,已知标杆BE高1.2 m,测得AB=1.6 m,BC=12.4 m,则建筑物CD的高是( )
A.9.3 m B.10.5 m C.12.4 m D.14 m
B
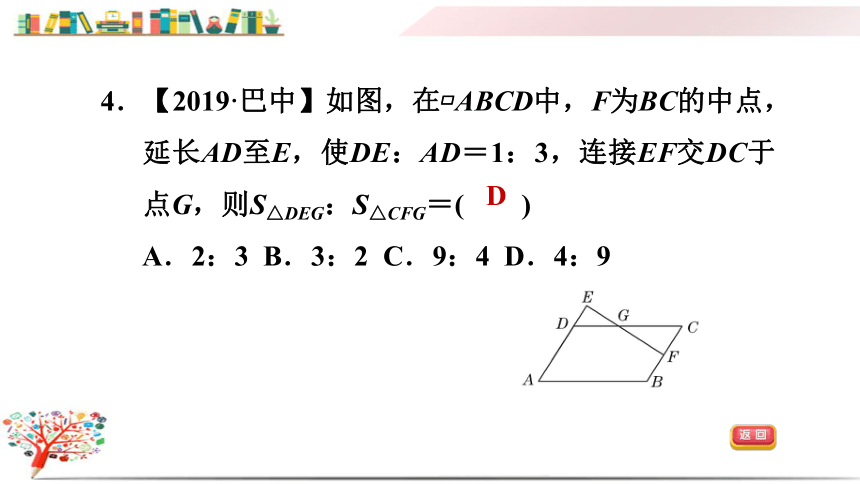
4.【2019·巴中】如图,在?ABCD中,F为BC的中点,延长AD至E,使DE:AD=1:3,连接EF交DC于点G,则S△DEG:S△CFG=( )
A.2:3 B.3:2 C.9:4 D.4:9
D
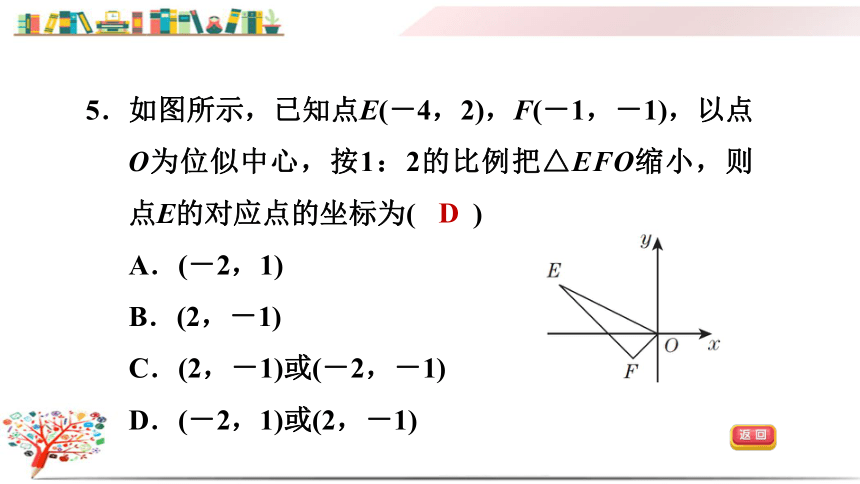
5.如图所示,已知点E(-4,2),F(-1,-1),以点O为位似中心,按1:2的比例把△EFO缩小,则点E的对应点的坐标为( )
A.(-2,1)
B.(2,-1)
C.(2,-1)或(-2,-1)
D.(-2,1)或(2,-1)
D
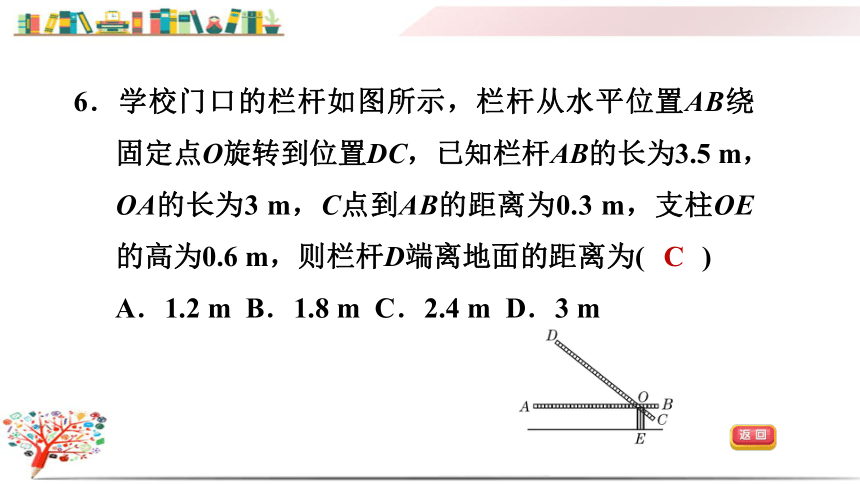
6.学校门口的栏杆如图所示,栏杆从水平位置AB绕固定点O旋转到位置DC,已知栏杆AB的长为3.5 m,OA的长为3 m,C点到AB的距离为0.3 m,支柱OE的高为0.6 m,则栏杆D端离地面的距离为( )
A.1.2 m B.1.8 m C.2.4 m D.3 m
C
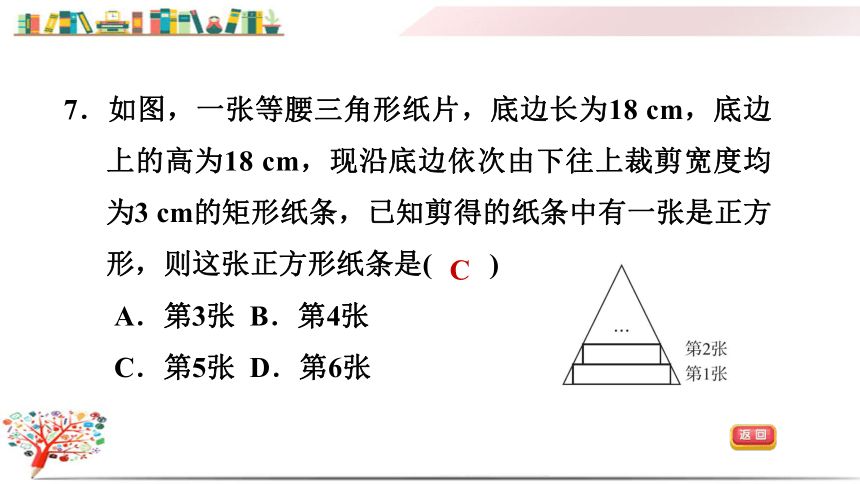
7.如图,一张等腰三角形纸片,底边长为18 cm,底边上的高为18 cm,现沿底边依次由下往上裁剪宽度均为3 cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第3张 B.第4张
C.第5张 D.第6张
C
【点拨】∵在?ABCD中,∠BCD=60°,∴∠BAD=60°,∠ADC=120°.∵DE平分∠ADC,
∴∠CDE=∠ADE=60°.∴∠DEA=60°.
【答案】B
10.如果两个相似三角形的最长边分别是35厘米和14厘米,它们的周长之差为60厘米,那么这两个三角形的周长分别是________________.
100厘米和40厘米
1:16
12.【中考·菏泽】如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,∠OCD=90°,∠AOB=60°,若点B的坐标是(6,0),则点C的坐标是________.
13.小华在学习了小孔成像的原理后,利用如图所示的装置来验证小孔成像的现象.已知一根点燃的蜡烛距小孔20 cm,光屏在距小孔30 cm处,小华测量了蜡烛的火焰高度为2 cm,则光屏上火焰所成像的高度为________cm.
3
14.如图,△ABC是一块正三角形余料,边长为120 mm,要把它加工成正方形零件,使正方形的一边QM在边BC上,其余两个顶点P、N分别在AB、AC上,则这个正方形零件的边长是________mm.
【点拨】如图,作△ABC的高AD,交PN于点E.
15.如图,用曲尺测量大坝的高度h,使OA,OB分别顶住地面和大坝的斜面CD,且OA与地面垂直,现量出OA=40 cm,OB=60 cm,AD=30 cm,CD=5 m,试求大坝的高度h.
解:如图,过点D作DE⊥OB于点E.
16.【2019·巴中】如图,△ABC在边长为1的正方形网格中.
(1)以点C为位似中心,作出△ABC的位似图形△A1B1C,使其相似比为1∶2,且△A1B1C位于点C的异侧,并表示出A1的坐标.
解:如图,△A1B1C就是所要画的三角形,点A1的坐标为(3,-3).
(2)作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.
解:如图,△A2B2C就是所要画的三角形.
(3)在(2)的条件下求出点B经过的路径长.
17.【2019·荆门】如图,为了测量一栋楼的高度OE,小明同学先在操场上A处放一面镜子,向后退到B处,恰好在镜子中看到楼的顶部E;再将镜子放到C处,然后后退到D处,恰好再次在镜子中看到楼的顶部E(点O,A,B,C,D在同一条直线上),测得AC=2 m,BD=2.1 m.如果小明眼睛距地面高度BF,
DG为1.6 m,试确定楼的高度OE.
证明:∵四边形ABCD为菱形,
∴BD平分∠ABC.∴∠ABC=2∠ABG.
又∵∠ABC=2∠BAM,
∴∠BAG=∠ABG.∴AG=BG.
18.【2021·合肥市48中月考】如图,四边形ABCD为菱形,M为BC上一点,连接AM交对角线BD于点G,并且∠ABC=2∠BAM.
(1)求证:AG=BG.
(2)若M为BC的中点,同时S△BGM=1,求△ADG的面积.
相似三角形的性质及应用
JJ版九年级上
第二十五章 图形的相似
4
提示:点击 进入习题
答案显示
6
1
2
3
5
C
B
D
C
C
D
8
7
B
C
提示:点击 进入习题
答案显示
9
12
10
11
100厘米和40厘米
14
13
3
16
15
见习题
见习题
1:16
提示:点击 进入习题
答案显示
17
见习题
18
见习题
1.如图,在平行四边形ABCD中,点E在CD上,若DE:CE=1:2,则△CEF与△ABF的周长比为( )
A.1:2 B.1:3 C.2:3 D.4:9
C
2.如图,点O是五边形ABCDE和五边形A1B1C1D1E1的位似中心,若OA:OA1=1:3,则C1D1:CD等于( )
A.1:2 B.1:3 C.3:1 D.4:1
C
3.【中考·临沂】如图,利用标杆BE测量建筑物的高度,已知标杆BE高1.2 m,测得AB=1.6 m,BC=12.4 m,则建筑物CD的高是( )
A.9.3 m B.10.5 m C.12.4 m D.14 m
B
4.【2019·巴中】如图,在?ABCD中,F为BC的中点,延长AD至E,使DE:AD=1:3,连接EF交DC于点G,则S△DEG:S△CFG=( )
A.2:3 B.3:2 C.9:4 D.4:9
D
5.如图所示,已知点E(-4,2),F(-1,-1),以点O为位似中心,按1:2的比例把△EFO缩小,则点E的对应点的坐标为( )
A.(-2,1)
B.(2,-1)
C.(2,-1)或(-2,-1)
D.(-2,1)或(2,-1)
D
6.学校门口的栏杆如图所示,栏杆从水平位置AB绕固定点O旋转到位置DC,已知栏杆AB的长为3.5 m,OA的长为3 m,C点到AB的距离为0.3 m,支柱OE的高为0.6 m,则栏杆D端离地面的距离为( )
A.1.2 m B.1.8 m C.2.4 m D.3 m
C
7.如图,一张等腰三角形纸片,底边长为18 cm,底边上的高为18 cm,现沿底边依次由下往上裁剪宽度均为3 cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第3张 B.第4张
C.第5张 D.第6张
C
【点拨】∵在?ABCD中,∠BCD=60°,∴∠BAD=60°,∠ADC=120°.∵DE平分∠ADC,
∴∠CDE=∠ADE=60°.∴∠DEA=60°.
【答案】B
10.如果两个相似三角形的最长边分别是35厘米和14厘米,它们的周长之差为60厘米,那么这两个三角形的周长分别是________________.
100厘米和40厘米
1:16
12.【中考·菏泽】如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,∠OCD=90°,∠AOB=60°,若点B的坐标是(6,0),则点C的坐标是________.
13.小华在学习了小孔成像的原理后,利用如图所示的装置来验证小孔成像的现象.已知一根点燃的蜡烛距小孔20 cm,光屏在距小孔30 cm处,小华测量了蜡烛的火焰高度为2 cm,则光屏上火焰所成像的高度为________cm.
3
14.如图,△ABC是一块正三角形余料,边长为120 mm,要把它加工成正方形零件,使正方形的一边QM在边BC上,其余两个顶点P、N分别在AB、AC上,则这个正方形零件的边长是________mm.
【点拨】如图,作△ABC的高AD,交PN于点E.
15.如图,用曲尺测量大坝的高度h,使OA,OB分别顶住地面和大坝的斜面CD,且OA与地面垂直,现量出OA=40 cm,OB=60 cm,AD=30 cm,CD=5 m,试求大坝的高度h.
解:如图,过点D作DE⊥OB于点E.
16.【2019·巴中】如图,△ABC在边长为1的正方形网格中.
(1)以点C为位似中心,作出△ABC的位似图形△A1B1C,使其相似比为1∶2,且△A1B1C位于点C的异侧,并表示出A1的坐标.
解:如图,△A1B1C就是所要画的三角形,点A1的坐标为(3,-3).
(2)作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.
解:如图,△A2B2C就是所要画的三角形.
(3)在(2)的条件下求出点B经过的路径长.
17.【2019·荆门】如图,为了测量一栋楼的高度OE,小明同学先在操场上A处放一面镜子,向后退到B处,恰好在镜子中看到楼的顶部E;再将镜子放到C处,然后后退到D处,恰好再次在镜子中看到楼的顶部E(点O,A,B,C,D在同一条直线上),测得AC=2 m,BD=2.1 m.如果小明眼睛距地面高度BF,
DG为1.6 m,试确定楼的高度OE.
证明:∵四边形ABCD为菱形,
∴BD平分∠ABC.∴∠ABC=2∠ABG.
又∵∠ABC=2∠BAM,
∴∠BAG=∠ABG.∴AG=BG.
18.【2021·合肥市48中月考】如图,四边形ABCD为菱形,M为BC上一点,连接AM交对角线BD于点G,并且∠ABC=2∠BAM.
(1)求证:AG=BG.
(2)若M为BC的中点,同时S△BGM=1,求△ADG的面积.
同课章节目录
