2021-2022学年苏科新版八年级上册数学《第2章 轴对称图形》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年苏科新版八年级上册数学《第2章 轴对称图形》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 305.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 11:22:38 | ||
图片预览

文档简介
2021-2022学年苏科新版八年级上册数学《第2章
轴对称图形》单元测试卷
一.选择题
1.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A.M点
B.N点
C.P点
D.Q点
2.如图,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为( )
A.30°
B.45°
C.60°
D.75°
3.“致中和,天地位焉,万物育焉.”对称美是我国古人和谐平衡思想的体现,常被运用于建筑、器物、绘画、标识等作品的设计上,使对称之美惊艳了千年的时光.在下列标识或简图中,是轴对称图形的是( )
A.
B.
C.
D.
4.小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,则电子表的实际时刻是( )
A.15:01
B.10:51
C.10:21
D.12:01
5.下列说法正确的是( )
A.轴对称图形是两个图形组成的
B.等边三角形有三条对称轴
C.两个全等的三角形组成一个轴对称图形
D.直角三角形一定是轴对称图形
6.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有( )
A.3个
B.4个
C.5个
D.6个
7.下列剪纸作品中,是轴对称图形的为( )
A.
B.
C.
D.
8.一张正方形的纸片,如图1进行两次对折,折成一个正方形,从右下角的顶点,沿斜虚线剪去一个角剪下的实际是四个小三角形,再把余下的部分展开,展开后的这个图形的内角和是多少度?( )
A.1080°
B.360°
C.180°
D.900°
9.如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )
A.9cm
B.13cm
C.16cm
D.10cm
10.桌面上有A,B两球,若要将B球射向桌面任意一边,使一次反弹后击中A球,则如图所示8个点中,可以瞄准的点有( )个.
A.1
B.2
C.4
D.6
二.填空题
11.如图,∠AOB=60°,CD⊥OA于D,CE⊥OB于E,且CD=CE,则∠DOC=
.
12.小华从镜子中看到身后电子钟的示数如图所示,则此时的时间应是
.
13.将一张正方形纸片按如图步骤,通过折叠得到图④,再沿虚线剪去一个角,展开铺平后得到图⑤,其中FM、GN是折痕,若正方形EFGH与五边形MCNGF面积相等,则的值是
.
14.如图,在一个规格为6×12(即6×12个小正方形)的球台上,有两个小球A,B.若击打小球A,经过球台边的反弹后,恰好击中小球B,那么小球A击出时,应瞄准球台边上的点
.(P1至P4点)
15.如图是跳棋盘,其中格点上的黑色点为棋子,剩余的格点上没有棋子.我们约定跳棋游戏的规则是:把跳棋棋子在棋盘内,沿着棋子对称跳行,跳行一次称为一步.已知点A为己方一枚棋子,欲将棋子A跳进对方区域(阴影部分的格点),则跳行的最少步数为
步.
16.等边三角形是一个轴对称图形,它有
条对称轴.
17.如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为
.
18.如图,直线m是多边形ABCDE的对称轴,其中∠A=120°,∠B=110°,那么∠BCD的度数为
.
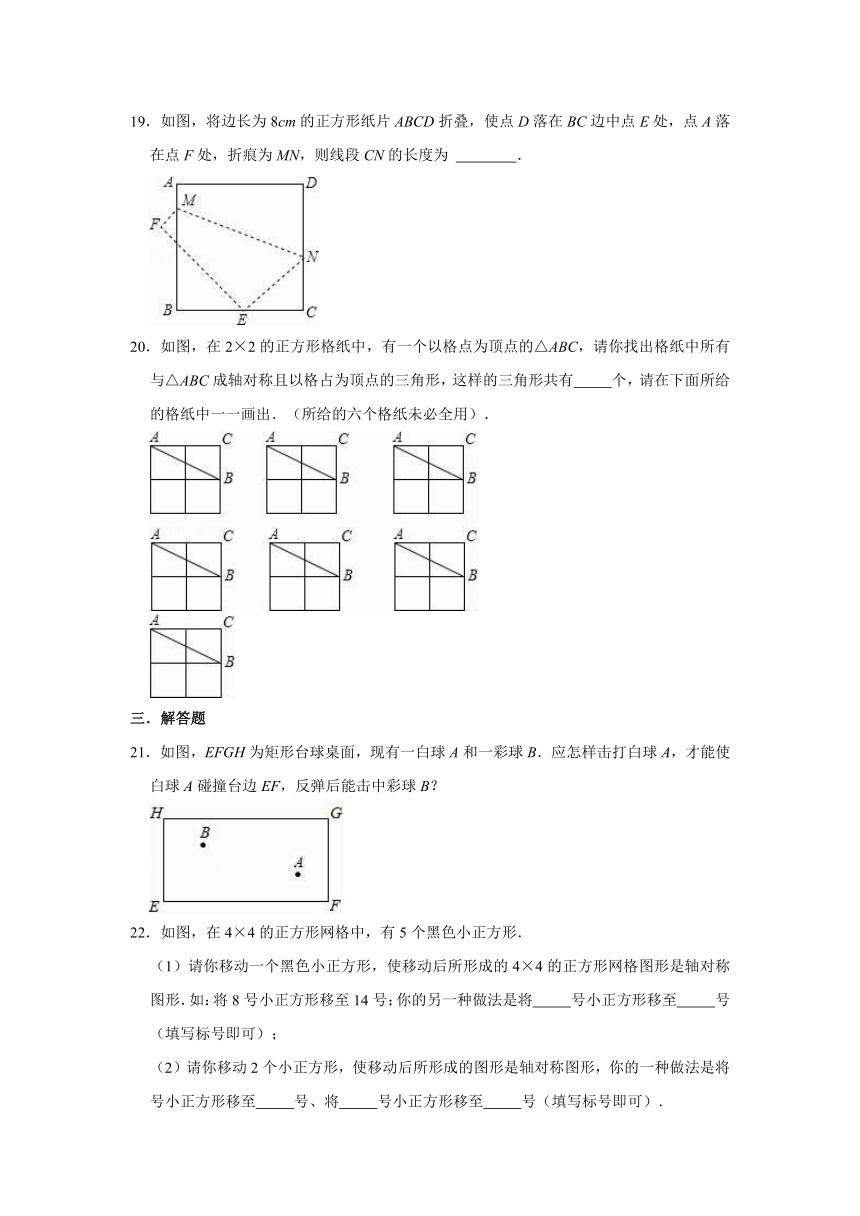
19.如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A落在点F处,折痕为MN,则线段CN的长度为
.
20.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且以格占为顶点的三角形,这样的三角形共有
个,请在下面所给的格纸中一一画出.(所给的六个格纸未必全用).
三.解答题
21.如图,EFGH为矩形台球桌面,现有一白球A和一彩球B.应怎样击打白球A,才能使白球A碰撞台边EF,反弹后能击中彩球B?
22.如图,在4×4的正方形网格中,有5个黑色小正方形.
(1)请你移动一个黑色小正方形,使移动后所形成的4×4的正方形网格图形是轴对称图形.如:将8号小正方形移至14号;你的另一种做法是将
号小正方形移至
号(填写标号即可);
(2)请你移动2个小正方形,使移动后所形成的图形是轴对称图形,你的一种做法是将
号小正方形移至
号、将
号小正方形移至
号(填写标号即可).
23.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.
24.如图,长方形台球桌ABCD上有两个球P,Q.
(1)请画出一条路径,使得球P撞击台球桌边AB反弹后,正好撞到球Q;
(2)请画出一条路径,使得球P撞击台球桌边,经过两次反弹后,正好撞到球Q;
25.今天是2003年9月1日,小明拿起一盒牛奶刚要喝,妈妈说:“儿子,牛奶保质期过了,别喝了”,小明从镜子里看到保质期的数字是,牛奶真的过期了吗?为什么?
26.如图,D、E分别是AB、AC的中点,CD⊥AB于D,BE⊥AC于E,求证:AC=AB.
27.如图,∠A=90°,E为BC上一点,A点和E点关于BD对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
参考答案与试题解析
一.选择题
1.解:从图上可以看出点M在∠AOB的平分线上,其它三点不在∠AOB的平分线上.
所以点M到∠AOB两边的距离相等.故选A.
2.解:要使白球反弹后能将黑球直接撞入袋中,
∠2+∠3=90°,
∵∠3=30°,
∴∠2=60°,
∴∠1=60°.
故选:C.
3.解:A、是轴对称图形,故此选项符合题意;
B、不是轴对称图形,故此选项不合题意;
C、不是轴对称图形,故此选项不合题意;
D、不是轴对称图形,故此选项不合题意;
故选:A.
4.解:电子表的实际时刻是10:21.
故选:C.
5.解:A、轴对称图形可以是1个图形,故错误;
B、等边三角形有三条对称轴,即三条中线,故正确;
C、两个全等的三角形不一定组成一个轴对称图形,故错误;
D、直角三角形不一定是轴对称图形,故错误.
故选:B.
6.解:与△ABC成轴对称且也以格点为顶点的三角形有5个,
分别为△BCD,△BFH,△ADC,△AEF,△CGH,
故选:C.
7.解:A、不是轴对称图形,故选项错误;
B、不是轴对称图形,故选项错误;
C、是轴对称图形,故选项正确;
D、不是轴对称图形,故选项错误.
故选:C.
8.解:展开图的这个图形是八边形,故内角和为:(8﹣2)×180°=1080°.
故选:A.
9.解:∵△BDE由△BDC翻折而成,
∴BE=BC=7cm,DE=CD,
∴AE=AB﹣BE=10﹣7=3cm,
∴△AED的周长=AE+(AD+DE)=AE+AC=3+6=9cm.
故选:A.
10.解:
由图可知可以瞄准的点有2个..
故选:B.
二.填空题
11.解:∵CD⊥OA于D,CE⊥OB于E,且CD=CE,
∴OC平分∠AOB,
即∠DOC=∠AOB=×60°=30°.
故本题答案为:30°.
12.解:方法一:将显示的像数字依次左右互换并将每一个数字左右反转,得到时间为21:05;
方法二:将显示的像后面正常读数为21:05就是此时的时间.
故答案为:21:05.
13.解:连接HF,设直线MH与AD边的交点为P,如图:
由折叠可知点P、H、F、M四点共线,且PH=MF,
设正方形ABCD的边长为2a,
则正方形ABCD的面积为4a2,
∵若正方形EFGH与五边形MCNGF的面积相等
∴由折叠可知正方形EFGH的面积=×正方形ABCD的面积=a2,
∴正方形EFGH的边长GF==a,
∴HF=GF=a,
∴MF=PH==a
∴==,
故答案为:.
14.解:
如图,应瞄准球台边上的点P2.
15.解:如图中红棋子所示,根据规则:
①点A从右边通过3次轴对称后,位于阴影部分内;
②点A从左边通过4次轴对称后,位于阴影部分内.
所以跳行的最少步数为3步.
16.解:等边三角形是一个轴对称图形,它有3条对称轴.
故答案为:3.
17.解:∵∠1:∠2:∠3=7:2:1,
∴设∠1=7x,∠2=2x,∠3=x,
由∠1+∠2+∠3=180°得:
7x+2x+x=180°,
解得x=18,
故∠1=7×18=126°,∠2=2×18=36°,∠3=1×18=18°,
∵△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的,
∴∠DCA=∠E=∠3=18°,∠2=∠EBA=∠D=36°,∠4=∠EBA+∠E=36°+18°=54°,
∠5=∠2+∠3=18°+36°=54°,
故∠EAC=∠4+∠5=54°+54°=108°,
在△EGF与△CAF中,∠E=∠DCA,∠DFE=∠CFA,
∴△EGF∽△CAF,
∴α=∠EAC=108°.
故答案为:108°.
18.解:∵直线m是多边形ABCDE的对称轴,
∴∠E=∠A=120°,∠D=∠B=110°,
∴∠BCD=540°﹣120°×2﹣110°×2=80°.
故答案为:80°
19.解:由题意设CN=x
cm,则EN=(8﹣x)cm,
又∵CE=DC=4cm,
∴在Rt△ECN中,EN2=EC2+CN2,即(8﹣x)2=42+x2,
解得:x=3,即CN=3cm.
故答案为:3cm.
20.解:与△ABC成轴对称且以格点为顶点的三角形如图:
共5个.
三.解答题
21.解:如图,作点A关于EF的对称点A′,连接A′B,交EF于点C,将白球A打到台边EF的点C处,反弹后能击中彩球B.
22.解:(1)移动一个黑色小正方形,使移动后所形成的4×4的正方形网格图形是轴对称图形,另一种做法是将9号小正方形移至3号;
(2)移动2个小正方形,使移动后所形成的图形是轴对称图形,做法是将9号小正方形移至3号、将13号小正方形移至4号(答案不唯一).
故答案为:9,3;9,3,13,4.
23.(1)证明:∵DE⊥AB于E,DF⊥AC于F,
∴∠E=∠DFC=90°,
∴△BDE与△CDF均为直角三角形,
∵
∴△BDE≌△CDF(HL).
∴DE=DF,即AD平分∠BAC;
(2)AB+AC=2AE.
证明:∵BE=CF,AD平分∠BAC,
∴∠EAD=∠CAD,
∵∠E=∠AFD=90°,
∴∠ADE=∠ADF.
在△AED与△AFD中,
∵,
∴△AED≌△AFD(ASA).
∴AE=AF.
∴AB+AC=AE﹣BE+AF+CF=AE+AE=2AE.
24.解:(1)如图,运动路径:P→M→Q,点M即为所求.
(2)如图,运动路径:P→E→F→Q,点E,点F即为所求.
25.解:
|20030824,
∴实际的保质期应是20030824,故牛奶已经过期.
26.证明:如图,连接BC
∵CD⊥AB于D,D是AB的中点,即CD垂直平分AB,
∴AC=BC(中垂线的性质),
∵E为AC中点,BE⊥AC,
∴BC=AB(中垂线的性质),
∴AC=AB.
27.解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD.
又B点、C点关于DE对称,
∴∠DBE=∠C,∠ABC=2∠C.
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°.
∴∠C=30°
∴∠ABC=2∠C=60°.
轴对称图形》单元测试卷
一.选择题
1.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A.M点
B.N点
C.P点
D.Q点
2.如图,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为( )
A.30°
B.45°
C.60°
D.75°
3.“致中和,天地位焉,万物育焉.”对称美是我国古人和谐平衡思想的体现,常被运用于建筑、器物、绘画、标识等作品的设计上,使对称之美惊艳了千年的时光.在下列标识或简图中,是轴对称图形的是( )
A.
B.
C.
D.
4.小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,则电子表的实际时刻是( )
A.15:01
B.10:51
C.10:21
D.12:01
5.下列说法正确的是( )
A.轴对称图形是两个图形组成的
B.等边三角形有三条对称轴
C.两个全等的三角形组成一个轴对称图形
D.直角三角形一定是轴对称图形
6.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有( )
A.3个
B.4个
C.5个
D.6个
7.下列剪纸作品中,是轴对称图形的为( )
A.
B.
C.
D.
8.一张正方形的纸片,如图1进行两次对折,折成一个正方形,从右下角的顶点,沿斜虚线剪去一个角剪下的实际是四个小三角形,再把余下的部分展开,展开后的这个图形的内角和是多少度?( )
A.1080°
B.360°
C.180°
D.900°
9.如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )
A.9cm
B.13cm
C.16cm
D.10cm
10.桌面上有A,B两球,若要将B球射向桌面任意一边,使一次反弹后击中A球,则如图所示8个点中,可以瞄准的点有( )个.
A.1
B.2
C.4
D.6
二.填空题
11.如图,∠AOB=60°,CD⊥OA于D,CE⊥OB于E,且CD=CE,则∠DOC=
.
12.小华从镜子中看到身后电子钟的示数如图所示,则此时的时间应是
.
13.将一张正方形纸片按如图步骤,通过折叠得到图④,再沿虚线剪去一个角,展开铺平后得到图⑤,其中FM、GN是折痕,若正方形EFGH与五边形MCNGF面积相等,则的值是
.
14.如图,在一个规格为6×12(即6×12个小正方形)的球台上,有两个小球A,B.若击打小球A,经过球台边的反弹后,恰好击中小球B,那么小球A击出时,应瞄准球台边上的点
.(P1至P4点)
15.如图是跳棋盘,其中格点上的黑色点为棋子,剩余的格点上没有棋子.我们约定跳棋游戏的规则是:把跳棋棋子在棋盘内,沿着棋子对称跳行,跳行一次称为一步.已知点A为己方一枚棋子,欲将棋子A跳进对方区域(阴影部分的格点),则跳行的最少步数为
步.
16.等边三角形是一个轴对称图形,它有
条对称轴.
17.如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为
.
18.如图,直线m是多边形ABCDE的对称轴,其中∠A=120°,∠B=110°,那么∠BCD的度数为
.
19.如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A落在点F处,折痕为MN,则线段CN的长度为
.
20.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且以格占为顶点的三角形,这样的三角形共有
个,请在下面所给的格纸中一一画出.(所给的六个格纸未必全用).
三.解答题
21.如图,EFGH为矩形台球桌面,现有一白球A和一彩球B.应怎样击打白球A,才能使白球A碰撞台边EF,反弹后能击中彩球B?
22.如图,在4×4的正方形网格中,有5个黑色小正方形.
(1)请你移动一个黑色小正方形,使移动后所形成的4×4的正方形网格图形是轴对称图形.如:将8号小正方形移至14号;你的另一种做法是将
号小正方形移至
号(填写标号即可);
(2)请你移动2个小正方形,使移动后所形成的图形是轴对称图形,你的一种做法是将
号小正方形移至
号、将
号小正方形移至
号(填写标号即可).
23.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.
24.如图,长方形台球桌ABCD上有两个球P,Q.
(1)请画出一条路径,使得球P撞击台球桌边AB反弹后,正好撞到球Q;
(2)请画出一条路径,使得球P撞击台球桌边,经过两次反弹后,正好撞到球Q;
25.今天是2003年9月1日,小明拿起一盒牛奶刚要喝,妈妈说:“儿子,牛奶保质期过了,别喝了”,小明从镜子里看到保质期的数字是,牛奶真的过期了吗?为什么?
26.如图,D、E分别是AB、AC的中点,CD⊥AB于D,BE⊥AC于E,求证:AC=AB.
27.如图,∠A=90°,E为BC上一点,A点和E点关于BD对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
参考答案与试题解析
一.选择题
1.解:从图上可以看出点M在∠AOB的平分线上,其它三点不在∠AOB的平分线上.
所以点M到∠AOB两边的距离相等.故选A.
2.解:要使白球反弹后能将黑球直接撞入袋中,
∠2+∠3=90°,
∵∠3=30°,
∴∠2=60°,
∴∠1=60°.
故选:C.
3.解:A、是轴对称图形,故此选项符合题意;
B、不是轴对称图形,故此选项不合题意;
C、不是轴对称图形,故此选项不合题意;
D、不是轴对称图形,故此选项不合题意;
故选:A.
4.解:电子表的实际时刻是10:21.
故选:C.
5.解:A、轴对称图形可以是1个图形,故错误;
B、等边三角形有三条对称轴,即三条中线,故正确;
C、两个全等的三角形不一定组成一个轴对称图形,故错误;
D、直角三角形不一定是轴对称图形,故错误.
故选:B.
6.解:与△ABC成轴对称且也以格点为顶点的三角形有5个,
分别为△BCD,△BFH,△ADC,△AEF,△CGH,
故选:C.
7.解:A、不是轴对称图形,故选项错误;
B、不是轴对称图形,故选项错误;
C、是轴对称图形,故选项正确;
D、不是轴对称图形,故选项错误.
故选:C.
8.解:展开图的这个图形是八边形,故内角和为:(8﹣2)×180°=1080°.
故选:A.
9.解:∵△BDE由△BDC翻折而成,
∴BE=BC=7cm,DE=CD,
∴AE=AB﹣BE=10﹣7=3cm,
∴△AED的周长=AE+(AD+DE)=AE+AC=3+6=9cm.
故选:A.
10.解:
由图可知可以瞄准的点有2个..
故选:B.
二.填空题
11.解:∵CD⊥OA于D,CE⊥OB于E,且CD=CE,
∴OC平分∠AOB,
即∠DOC=∠AOB=×60°=30°.
故本题答案为:30°.
12.解:方法一:将显示的像数字依次左右互换并将每一个数字左右反转,得到时间为21:05;
方法二:将显示的像后面正常读数为21:05就是此时的时间.
故答案为:21:05.
13.解:连接HF,设直线MH与AD边的交点为P,如图:
由折叠可知点P、H、F、M四点共线,且PH=MF,
设正方形ABCD的边长为2a,
则正方形ABCD的面积为4a2,
∵若正方形EFGH与五边形MCNGF的面积相等
∴由折叠可知正方形EFGH的面积=×正方形ABCD的面积=a2,
∴正方形EFGH的边长GF==a,
∴HF=GF=a,
∴MF=PH==a
∴==,
故答案为:.
14.解:
如图,应瞄准球台边上的点P2.
15.解:如图中红棋子所示,根据规则:
①点A从右边通过3次轴对称后,位于阴影部分内;
②点A从左边通过4次轴对称后,位于阴影部分内.
所以跳行的最少步数为3步.
16.解:等边三角形是一个轴对称图形,它有3条对称轴.
故答案为:3.
17.解:∵∠1:∠2:∠3=7:2:1,
∴设∠1=7x,∠2=2x,∠3=x,
由∠1+∠2+∠3=180°得:
7x+2x+x=180°,
解得x=18,
故∠1=7×18=126°,∠2=2×18=36°,∠3=1×18=18°,
∵△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的,
∴∠DCA=∠E=∠3=18°,∠2=∠EBA=∠D=36°,∠4=∠EBA+∠E=36°+18°=54°,
∠5=∠2+∠3=18°+36°=54°,
故∠EAC=∠4+∠5=54°+54°=108°,
在△EGF与△CAF中,∠E=∠DCA,∠DFE=∠CFA,
∴△EGF∽△CAF,
∴α=∠EAC=108°.
故答案为:108°.
18.解:∵直线m是多边形ABCDE的对称轴,
∴∠E=∠A=120°,∠D=∠B=110°,
∴∠BCD=540°﹣120°×2﹣110°×2=80°.
故答案为:80°
19.解:由题意设CN=x
cm,则EN=(8﹣x)cm,
又∵CE=DC=4cm,
∴在Rt△ECN中,EN2=EC2+CN2,即(8﹣x)2=42+x2,
解得:x=3,即CN=3cm.
故答案为:3cm.
20.解:与△ABC成轴对称且以格点为顶点的三角形如图:
共5个.
三.解答题
21.解:如图,作点A关于EF的对称点A′,连接A′B,交EF于点C,将白球A打到台边EF的点C处,反弹后能击中彩球B.
22.解:(1)移动一个黑色小正方形,使移动后所形成的4×4的正方形网格图形是轴对称图形,另一种做法是将9号小正方形移至3号;
(2)移动2个小正方形,使移动后所形成的图形是轴对称图形,做法是将9号小正方形移至3号、将13号小正方形移至4号(答案不唯一).
故答案为:9,3;9,3,13,4.
23.(1)证明:∵DE⊥AB于E,DF⊥AC于F,
∴∠E=∠DFC=90°,
∴△BDE与△CDF均为直角三角形,
∵
∴△BDE≌△CDF(HL).
∴DE=DF,即AD平分∠BAC;
(2)AB+AC=2AE.
证明:∵BE=CF,AD平分∠BAC,
∴∠EAD=∠CAD,
∵∠E=∠AFD=90°,
∴∠ADE=∠ADF.
在△AED与△AFD中,
∵,
∴△AED≌△AFD(ASA).
∴AE=AF.
∴AB+AC=AE﹣BE+AF+CF=AE+AE=2AE.
24.解:(1)如图,运动路径:P→M→Q,点M即为所求.
(2)如图,运动路径:P→E→F→Q,点E,点F即为所求.
25.解:
|20030824,
∴实际的保质期应是20030824,故牛奶已经过期.
26.证明:如图,连接BC
∵CD⊥AB于D,D是AB的中点,即CD垂直平分AB,
∴AC=BC(中垂线的性质),
∵E为AC中点,BE⊥AC,
∴BC=AB(中垂线的性质),
∴AC=AB.
27.解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD.
又B点、C点关于DE对称,
∴∠DBE=∠C,∠ABC=2∠C.
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°.
∴∠C=30°
∴∠ABC=2∠C=60°.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
