2021-2022学年人教版数学八年级上册 12.3 角的平分线的性质 同步检测 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册 12.3 角的平分线的性质 同步检测 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 515.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 00:00:00 | ||
图片预览


文档简介
12.3 角的平分线的性质
一、选择题(共7小题;共35分)
1. 如图,OP 平分 ∠MON,PA⊥ON 于点 A,点 Q 是射线 OM 上的一个动点,若 PA=2,则 PQ 的最小值为 ??
A. 1 B. 2 C. 3 D. 4
2. 如图,△ABC 中,∠ACB=90?,BE 平分 ∠ABC,DE⊥AB,垂足为 D,如果 AC=12?cm,AD=8?cm,那么 △ADE 的周长为 ??
A. 22?cm B. 17?cm C. 20?cm D. 18?cm
3. 到三角形三边距离相等的点是 ??
A. 三角形三条高线的交点 B. 三角形三条中线的交点
C. 三角形三条角平分线的交点 D. 不存在这个点
4. 如图,在直角坐标系中,AD 是 Rt△OAB 的角平分线,点 D 的坐标是 0,?3,那么点 D 到 AB 的距离是 ??
A. 3 B. ?3 C. 2 D. ?2
5. 如图所示,下列推理中正确的个数是 ??
①因为 OC 平分 ∠AOB,点 P,D,E 分别在 OC,OA,OB 上,
所以 PD=PE;
②因为点 P 在 OC 上,PD⊥OA,PE⊥OB,
所以 PD=PE;
③因为点 P 在 OC 上,PD⊥OA,PE⊥OB,且 OC 平分 ∠AOB,
所以 PD=PE.
A. 0 个 B. 1 个 C. 2 个 D. 3 个
6. 如图,Rt△ABC 中,∠C=90?,AD 平分 ∠BAC,交 BC 于点 D,AB=10,S△ABD=15,则 CD 的长为 ??
A. 3 B. 4 C. 5 D. 6
7. 如图,在 △ABC 中,∠BAC,∠ABC 的平分线 AF,BE 交于点 O,连接 CO 并延长交 AB 边于点 D,则 CD 是 △ABC 的 ??
A. 角平分线 B. 中线 C. 高 D. 以上都不对
二、填空题(共8小题;共40分)
8. 已知点 P 在 ∠AOB 的平分线上,且点 P 到 OA 的距离为 3?cm,则点 P 到 OB 的距离为 ? cm.
9. 如图,∠AOB 的平分线上一点 P 到 OA 的距离为 5,Q 是 OB 上任意一点,则 PQ 的范围是 ?.
10. 如图,点 P 到 ∠AOB 两边的距离相等,若 ∠AOB=50?,则 ∠AOP= ?.
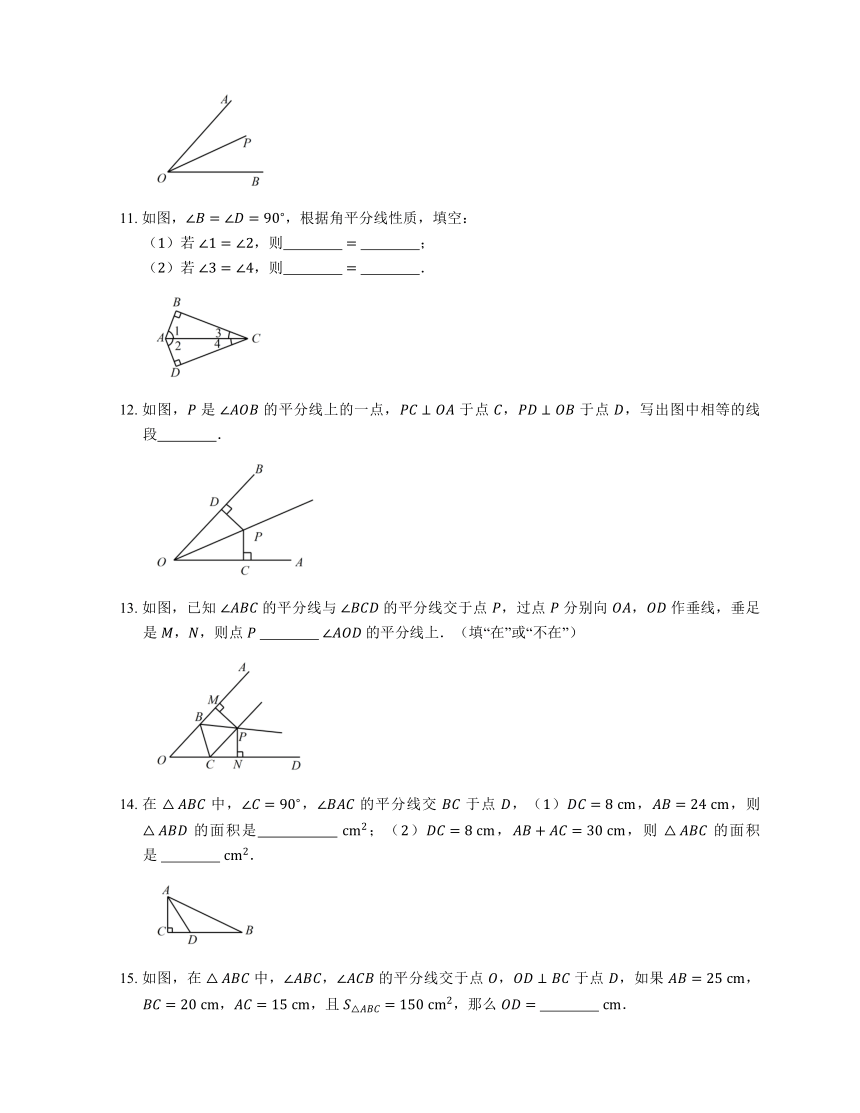
11. 如图,∠B=∠D=90?,根据角平分线性质,填空:
(1)若 ∠1=∠2,则 ? = ?;
(2)若 ∠3=∠4,则 ? = ?.
12. 如图,P 是 ∠AOB 的平分线上的一点,PC⊥OA 于点 C,PD⊥OB 于点 D,写出图中相等的线段 ?.
13. 如图,已知 ∠ABC 的平分线与 ∠BCD 的平分线交于点 P,过点 P 分别向 OA,OD 作垂线,垂足是 M,N,则点 P ? ∠AOD 的平分线上.(填“在”或“不在”)
14. 在 △ABC 中,∠C=90?,∠BAC 的平分线交 BC 于点 D,(1)DC=8?cm,AB=24?cm,则 △ABD 的面积是 ? cm2;(2)DC=8?cm,AB+AC=30?cm,则 △ABC 的面积是 ? cm2.
15. 如图,在 △ABC 中,∠ABC,∠ACB 的平分线交于点 O,OD⊥BC 于点 D,如果 AB=25?cm,BC=20?cm,AC=15?cm,且 S△ABC=150?cm2,那么 OD= ? cm.
三、解答题(共6小题;16题10分,17-21题各13分,共75分)
16. 如图,已知 ∠AOB,求作:∠AOB 的平分线 OC.
17. 如图,已知 △ABC 中,∠B=∠C,D 是 BC 中点,DE⊥AB 于点 E,DF⊥AC 于点 F.求证:AD 平分 ∠BAC.
18. 如图,已知 CD⊥AB 于点 D,BE⊥AC 于点 E,CD,BE 交于 O,∠1=∠2.求证 OB=OC.
19. 已知,如图,AB=AC,BD=CD,DE⊥AB 于点 E,DF⊥AC 于点 F.求证 DE=DF.
20. 如图,CD⊥AD,BA⊥AD,∠BCA=∠BAC.又 AE⊥BC,垂足为 E.求证 CD=CE.
21. 如图,已知 ∠B=∠C=90?,M 是 BC 中点,AM 平分 ∠DAB.求证:DM 平分 ∠ADC.
答案
1. B 【解析】当 PQ⊥OM 时,PQ 有最小值,
∵OP 平分 ∠MON,PA⊥ON,
∴PQ=PA=2.
2. C
3. C
4. A
5. B
6. A
7. A
8. 3
9. PQ≥5
10. 25?
11. BC,DC,AB,AD
12. PC=PD,OC=OD
13. 在
14. 96,120
15. 5
16.
作法:
①以O为圆心,任意长为半径,画弧交AO,BO于点M,N;
②再分别以M、N为圆心,适当长为半径画弧,交于点P;
③连接OP,射线OP即为所求.
17. 易证 △BDE≌△CDFAAS,得到 DE=DF,
根据角平分线的判定得到点 D 在 ∠BAC 的平分线上,即 AD 平分 ∠BAC.
18. ∵ CD⊥AB,BE⊥AC,∠1=∠2,OA=OA,
∴ △DOA≌△EOA .
∴ OD=OE .
∵ ∠DOB=∠EOC,
∵ △DOB≌△EOCASA,
∴ OB=OC.
19. 连接 AD,在 △ACD 和 △ABD 中,
AC=AB,CD=BD,AD=AD,
∴ △ACD≌△ABDSSS.
∴ ∠EAD=∠FAD,即 AD 平分 ∠EAF.
∵ DE⊥AE,DF⊥AF,
∴ DE=DF.
20. 因为 BA⊥AD,
所以 ∠DAB=90?,则 ∠BAC+∠DAC=∠DAB=90?.
因为 AE⊥BC,
所以 ∠BCA+∠CAE=90?.
因为 ∠BCA=∠BAC,
所以 ∠BAC+∠CAE=90?.
又因为 ∠CAE+∠DAC+∠EAB=90?,
所以 ∠DAC=∠CAE.
所以 AC 是 ∠EAD 的平分线.
又因为 CD⊥AD,AE⊥BC,
所以 CD=CE.
21.
如图,过点 M 作 ME⊥AD 于点 E,根据角平分线定理有 MB=ME,
根据已知条件有 ME=MC,则点 M 在 ∠ADC 的平分线上,即 DM 平分 ∠ADC.
一、选择题(共7小题;共35分)
1. 如图,OP 平分 ∠MON,PA⊥ON 于点 A,点 Q 是射线 OM 上的一个动点,若 PA=2,则 PQ 的最小值为 ??
A. 1 B. 2 C. 3 D. 4
2. 如图,△ABC 中,∠ACB=90?,BE 平分 ∠ABC,DE⊥AB,垂足为 D,如果 AC=12?cm,AD=8?cm,那么 △ADE 的周长为 ??
A. 22?cm B. 17?cm C. 20?cm D. 18?cm
3. 到三角形三边距离相等的点是 ??
A. 三角形三条高线的交点 B. 三角形三条中线的交点
C. 三角形三条角平分线的交点 D. 不存在这个点
4. 如图,在直角坐标系中,AD 是 Rt△OAB 的角平分线,点 D 的坐标是 0,?3,那么点 D 到 AB 的距离是 ??
A. 3 B. ?3 C. 2 D. ?2
5. 如图所示,下列推理中正确的个数是 ??
①因为 OC 平分 ∠AOB,点 P,D,E 分别在 OC,OA,OB 上,
所以 PD=PE;
②因为点 P 在 OC 上,PD⊥OA,PE⊥OB,
所以 PD=PE;
③因为点 P 在 OC 上,PD⊥OA,PE⊥OB,且 OC 平分 ∠AOB,
所以 PD=PE.
A. 0 个 B. 1 个 C. 2 个 D. 3 个
6. 如图,Rt△ABC 中,∠C=90?,AD 平分 ∠BAC,交 BC 于点 D,AB=10,S△ABD=15,则 CD 的长为 ??
A. 3 B. 4 C. 5 D. 6
7. 如图,在 △ABC 中,∠BAC,∠ABC 的平分线 AF,BE 交于点 O,连接 CO 并延长交 AB 边于点 D,则 CD 是 △ABC 的 ??
A. 角平分线 B. 中线 C. 高 D. 以上都不对
二、填空题(共8小题;共40分)
8. 已知点 P 在 ∠AOB 的平分线上,且点 P 到 OA 的距离为 3?cm,则点 P 到 OB 的距离为 ? cm.
9. 如图,∠AOB 的平分线上一点 P 到 OA 的距离为 5,Q 是 OB 上任意一点,则 PQ 的范围是 ?.
10. 如图,点 P 到 ∠AOB 两边的距离相等,若 ∠AOB=50?,则 ∠AOP= ?.
11. 如图,∠B=∠D=90?,根据角平分线性质,填空:
(1)若 ∠1=∠2,则 ? = ?;
(2)若 ∠3=∠4,则 ? = ?.
12. 如图,P 是 ∠AOB 的平分线上的一点,PC⊥OA 于点 C,PD⊥OB 于点 D,写出图中相等的线段 ?.
13. 如图,已知 ∠ABC 的平分线与 ∠BCD 的平分线交于点 P,过点 P 分别向 OA,OD 作垂线,垂足是 M,N,则点 P ? ∠AOD 的平分线上.(填“在”或“不在”)
14. 在 △ABC 中,∠C=90?,∠BAC 的平分线交 BC 于点 D,(1)DC=8?cm,AB=24?cm,则 △ABD 的面积是 ? cm2;(2)DC=8?cm,AB+AC=30?cm,则 △ABC 的面积是 ? cm2.
15. 如图,在 △ABC 中,∠ABC,∠ACB 的平分线交于点 O,OD⊥BC 于点 D,如果 AB=25?cm,BC=20?cm,AC=15?cm,且 S△ABC=150?cm2,那么 OD= ? cm.
三、解答题(共6小题;16题10分,17-21题各13分,共75分)
16. 如图,已知 ∠AOB,求作:∠AOB 的平分线 OC.
17. 如图,已知 △ABC 中,∠B=∠C,D 是 BC 中点,DE⊥AB 于点 E,DF⊥AC 于点 F.求证:AD 平分 ∠BAC.
18. 如图,已知 CD⊥AB 于点 D,BE⊥AC 于点 E,CD,BE 交于 O,∠1=∠2.求证 OB=OC.
19. 已知,如图,AB=AC,BD=CD,DE⊥AB 于点 E,DF⊥AC 于点 F.求证 DE=DF.
20. 如图,CD⊥AD,BA⊥AD,∠BCA=∠BAC.又 AE⊥BC,垂足为 E.求证 CD=CE.
21. 如图,已知 ∠B=∠C=90?,M 是 BC 中点,AM 平分 ∠DAB.求证:DM 平分 ∠ADC.
答案
1. B 【解析】当 PQ⊥OM 时,PQ 有最小值,
∵OP 平分 ∠MON,PA⊥ON,
∴PQ=PA=2.
2. C
3. C
4. A
5. B
6. A
7. A
8. 3
9. PQ≥5
10. 25?
11. BC,DC,AB,AD
12. PC=PD,OC=OD
13. 在
14. 96,120
15. 5
16.
作法:
①以O为圆心,任意长为半径,画弧交AO,BO于点M,N;
②再分别以M、N为圆心,适当长为半径画弧,交于点P;
③连接OP,射线OP即为所求.
17. 易证 △BDE≌△CDFAAS,得到 DE=DF,
根据角平分线的判定得到点 D 在 ∠BAC 的平分线上,即 AD 平分 ∠BAC.
18. ∵ CD⊥AB,BE⊥AC,∠1=∠2,OA=OA,
∴ △DOA≌△EOA .
∴ OD=OE .
∵ ∠DOB=∠EOC,
∵ △DOB≌△EOCASA,
∴ OB=OC.
19. 连接 AD,在 △ACD 和 △ABD 中,
AC=AB,CD=BD,AD=AD,
∴ △ACD≌△ABDSSS.
∴ ∠EAD=∠FAD,即 AD 平分 ∠EAF.
∵ DE⊥AE,DF⊥AF,
∴ DE=DF.
20. 因为 BA⊥AD,
所以 ∠DAB=90?,则 ∠BAC+∠DAC=∠DAB=90?.
因为 AE⊥BC,
所以 ∠BCA+∠CAE=90?.
因为 ∠BCA=∠BAC,
所以 ∠BAC+∠CAE=90?.
又因为 ∠CAE+∠DAC+∠EAB=90?,
所以 ∠DAC=∠CAE.
所以 AC 是 ∠EAD 的平分线.
又因为 CD⊥AD,AE⊥BC,
所以 CD=CE.
21.
如图,过点 M 作 ME⊥AD 于点 E,根据角平分线定理有 MB=ME,
根据已知条件有 ME=MC,则点 M 在 ∠ADC 的平分线上,即 DM 平分 ∠ADC.
