2021-2022学年湘教新版八年级上册数学《第2章 三角形》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年湘教新版八年级上册数学《第2章 三角形》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 217.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 00:00:00 | ||
图片预览



文档简介
2021-2022学年湘教新版八年级上册数学《第2章
三角形》单元测试卷
一.选择题
1.如图,共有三角形的个数是( )
A.3
B.4
C.5
D.6
2.三角形按角分类可以分为( )
A.锐角三角形、直角三角形、钝角三角形
B.等腰三角形、等边三角形、不等边三角形
C.直角三角形、等边直角三角形
D.以上答案都不正确
3.下列叙述中错误的一项是( )
A.三角形的中线、角平分线、高都是线段
B.三角形的三条高线中至少存在一条在三角形内部
C.只有一条高在三角形内部的三角形一定是钝角三角形
D.三角形的三条角平分线都在三角形内部
4.三角形的重心是( )
A.三角形三条角平分线的交点
B.三角形三条中线的交点
C.三角形三条边的垂直平分线的交点
D.三角形三条高的交点
5.下列长度的三条线段能组成三角形的是( )
A.3,4,8
B.5,6,11
C.5,6,10
D.1,2,3
6.等边三角形是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等腰直角三角形
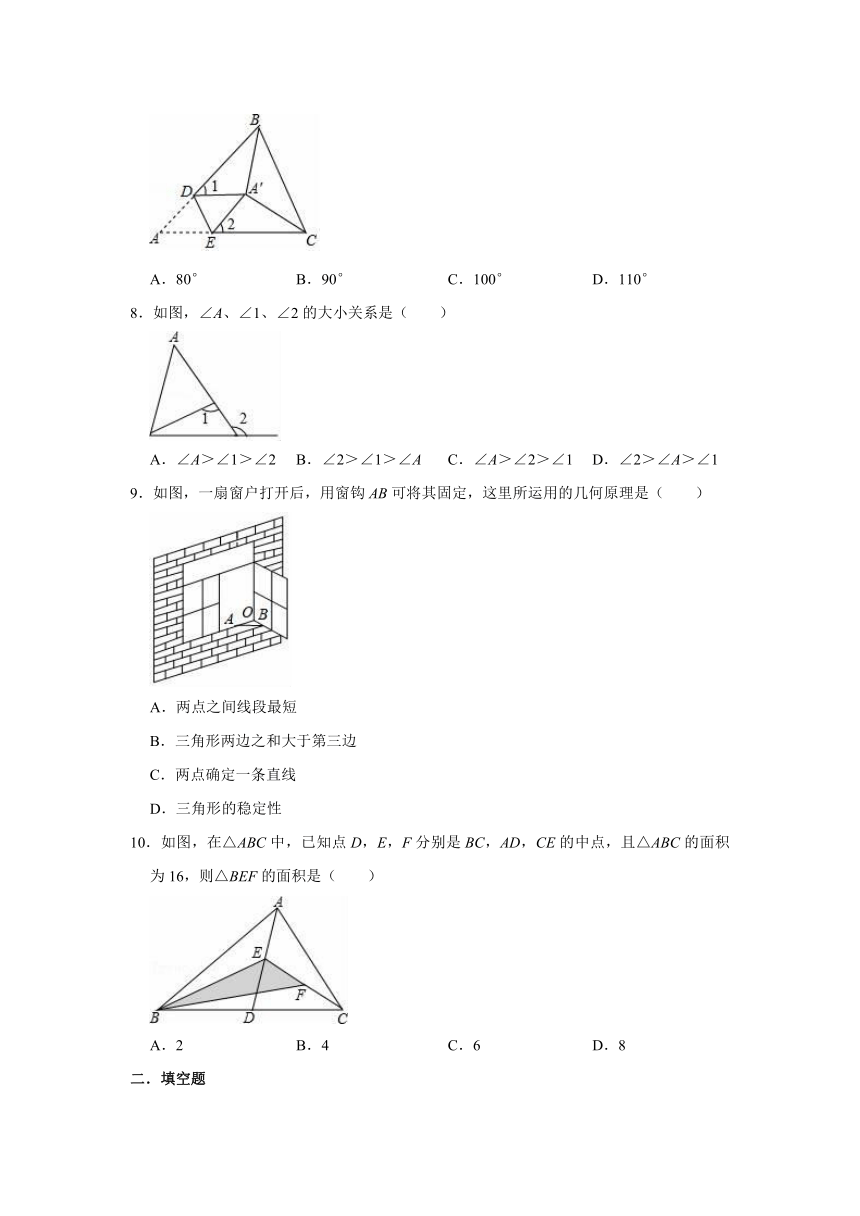
7.如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=110°,则∠1+∠2的度数为( )
A.80°
B.90°
C.100°
D.110°
8.如图,∠A、∠1、∠2的大小关系是( )
A.∠A>∠1>∠2
B.∠2>∠1>∠A
C.∠A>∠2>∠1
D.∠2>∠A>∠1
9.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
A.两点之间线段最短
B.三角形两边之和大于第三边
C.两点确定一条直线
D.三角形的稳定性
10.如图,在△ABC中,已知点D,E,F分别是BC,AD,CE的中点,且△ABC的面积为16,则△BEF的面积是( )
A.2
B.4
C.6
D.8
二.填空题
11.BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是
.
12.如图,木工师傅做好一门框后钉上木条AB,CD,使门框不变形,这种做法依据的数学原理是
.
13.一个三角形有两边分别为4cm和8cm,则第三边长x的取值范围
.
14.如图,∠1=115°,∠2=50°,那么∠3=
.
15.如图,直角ABC的周长为2008,在其内部有五个小直角三角形,则这五个小直角三角形的周长为
.
16.三角形的三条
交于一点,这点叫做三角形的重心.
17.将一副三角板如图所示摆放(其中一块三角板的一条直角边与另一块三角板的斜边摆放在一直线上),那么图中∠α=
度.
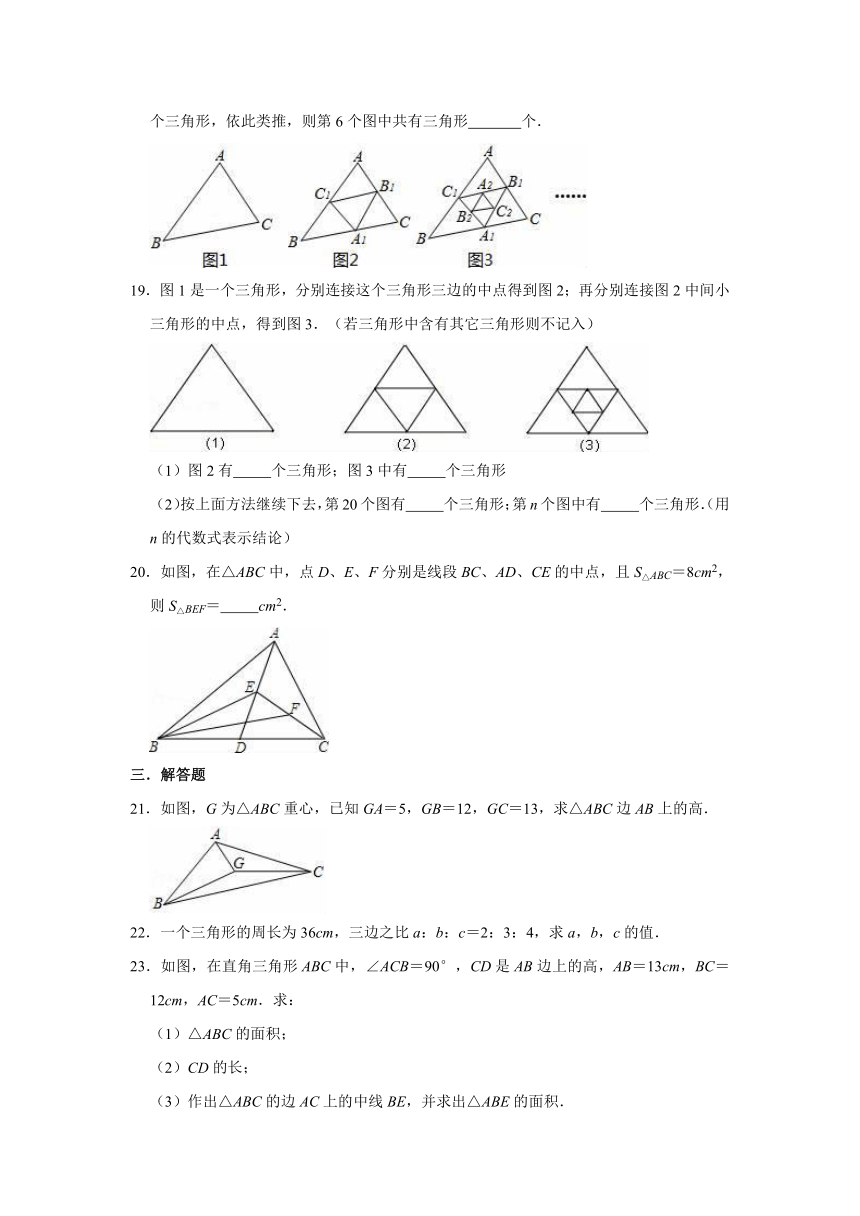
18.如图所示,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依此类推,则第6个图中共有三角形
个.
19.图1是一个三角形,分别连接这个三角形三边的中点得到图2;再分别连接图2中间小三角形的中点,得到图3.(若三角形中含有其它三角形则不记入)
(1)图2有
个三角形;图3中有
个三角形
(2)按上面方法继续下去,第20个图有
个三角形;第n个图中有
个三角形.(用n的代数式表示结论)
20.如图,在△ABC中,点D、E、F分别是线段BC、AD、CE的中点,且S△ABC=8cm2,则S△BEF=
cm2.
三.解答题
21.如图,G为△ABC重心,已知GA=5,GB=12,GC=13,求△ABC边AB上的高.
22.一个三角形的周长为36cm,三边之比a:b:c=2:3:4,求a,b,c的值.
23.如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm.求:
(1)△ABC的面积;
(2)CD的长;
(3)作出△ABC的边AC上的中线BE,并求出△ABE的面积.
24.(1)下列图形中具有稳定性是
;(只填图形序号)
(2)对不具有稳定性的图形,请适当地添加线段,使之具有稳定性.
25.一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
26.两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为
个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2006时,按上述规则画出的图形中,最少有多少个三角形?
27.在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.
参考答案与试题解析
一.选择题
1.解:图中有:△ABC,△ABD,△ABE,△ACD,△ACE,△ADE,共6个.
故选:D.
2.解:三角形按角分类可以分为锐角三角形、直角三角形、钝角三角形,
故选:A.
3.解:A、三角形的角平分线、中线、高都是线段,故此选项正确;
B、锐角三角形的三条高都在三角形的内部;直角三角形的一条高在三角形的内部,两条就是直角边;钝角三角形的一条高在三角形的内部,两条高在三角形的外部.故此选项正确;
C、根据B中的分析,知只有一条高在三角形内部的三角形可能是直角三角形,也可能是钝角三角形.故此选项错误;
D、根据角平分线的定义,知三角形的三条角平分线都在三角形的内部.故此选项正确.
故选:C.
4.解:三角形的重心是三角形三条中线的交点.
故选:B.
5.解:3+4<8,则3,4,8不能组成三角形,A不符合题意;
5+6=11,则5,6,11不能组成三角形,B不合题意;
5+6>10,则5,6,10能组成三角形,C符合题意;
1+2=3,则1,2,3不能组成三角形,D不合题意,
故选:C.
6.解:等边三角形的三个内角都是60度,属于锐角三角形;等边三角形的三条边都相等,属于等腰三角形.观察选项,选项B符合题意.
故选:B.
7.解:连接AA′.
∵A'B平分∠ABC,A'C平分∠ACB,∠BA'C=110°,
∴∠A′BC+∠A′CB=70°,
∴∠ABC+∠ACB=140°,
∴∠BAC=180°﹣140°=40°,
∵∠1=∠DAA′+∠DA′A,∠2=∠EAA′+∠EA′A,
∵∠DAA′=∠DA′A,∠EAA′=∠EA′A,
∴∠1+∠2=2(∠DAA′+∠EAA′)=2∠BAC=80°,
故选:A.
8.解:∵∠1是三角形的一个外角,∴∠1>∠A,
又∵∠2是三角形的一个外角,∴∠2>∠1,
∴∠2>∠1>∠A.
故选:B.
9.解:根据三角形的稳定性可固定窗户.
故选:D.
10.解:如图,点F是CE的中点,
∴△BEF的底是EF,△BEC的底是EC,即EF=EC,高相等;
∴S△BEF=S△BEC,
同理得,S△DEC=S△ADC,S△DEB=S△ADB,
∴S△EBC=S△ABC,
∴S△BEF=S△ABC,且S△ABC=16,
∴S△BEF=4,
即阴影部分的面积为4.
故选:B.
二.填空题
11.解:∵BD是△ABC的中线,
∴AD=CD,
∴△ABD和△BCD的周长的差=(AB+BD+AD)﹣(BC+BD+CD)=AB﹣BC,
∵AB=5,BC=3,
∴△ABD和△BCD的周长的差=5﹣3=2.
故答案为:2.
12.解:木工师傅做好一门框后钉上木条AB,CD,使门框不变形,这种做法依据的数学原理是三角形的稳定性.
故答案为:三角形的稳定性.
13.解:∵三角形的两边的长分别为4cm和8cm,第三边的长为x,
∴根据三角形的三边关系,得:8﹣4<x<4+8,即:4cm<x<12cm.
故答案为:4cm<x<12cm.
14.解:∵∠1=115°,∠2=50°,
∴∠3=∠1﹣∠2=65°,
故答案为:65°.
15.解:∵五个小直角三角形与大三角形相似,
∴对应边的比相等,
∵五个小三角形的斜边长的和等于大三角形的斜边长,
∴五个小三角形的周长的和等于大三角形的周长为2008.
16.解:三角形的三条中线交于一点,这点叫做三角形的重心.
故答案为:中线.
17.解:∵∠1=45°,∠2=60°,
∴∠α=180°﹣45°﹣60°=75°,
故答案为75.
18.解:第n个图形中,三角形的个数是1+4(n﹣1)=4n﹣3.所以当n=6时,原式=21,
故答案为:21.
19.解:(1)图2有4个三角形;图3中有7个三角形;
(2)按上面方法继续下去,可以得到(4)比(3)增加了4个三角形,
依此类推,第20个图有3×20﹣2=58个三角形;第n个图中有(3n﹣2)个三角形.
故答案为:(1)4;7;(2)58;(3n﹣2)
20.解:∵点E是AD的中点,
∴S△ABE=S△ABD,S△ACE=S△ADC,
∴S△ABE+S△ACE=S△ABC=×8=4,
∴S△BCE=S△ABC=×8=4,
∵点F是CE的中点,
∴S△BEF=S△BCE=×4=2.
故答案为:2.
三.解答题
21.解:延长AG至E,使GD=DE,作CH⊥AB于点G.
∵G为△ABC重心,
∴AG=2GD=GE,BD=DC.
∴△BGD≌△CED(SAS).
∴∠BGE=∠GEC,EC=BG=12.
∵GC2=EG2+EC2,
∴∠BGE=∠GEC=90°.
∴S△ABD===45,
由勾股定理得
AB===13,
∴S△ABC=2S△ABD=90.
∴CH==.
22.解:设三边长分别为2x,3x,4x,
由题意得,2x+3x+4x=36,
解得:x=4.
则a=2×4=8(cm),
b=3×4=12(cm),
c=4×4=16(cm).
23.解:(1)∵∠ACB=90°,BC=12cm,AC=5cm,
∴S△ABC=BC×AC=30cm2,
(2)∵S△ABC=AB×CD=30cm2,
∴CD=30÷AB=cm,
(3)S△ABE=S△ABC=×30=15cm2
24.解:(1)具有稳定性的是①④⑥三个.
(2)如图所示:
25.解:(1)当6是腰时,底边=20﹣6×2=8cm,即其它两边是6cm,8cm,此时6+6=12,能构成三角形;
(2)当6是底边时,腰=(20﹣6)÷2=7cm,此时能构成三角形,所以其它两边是7cm、7cm.
因此其它两边长分别为7cm,7cm,
综上所述两边长分别为6cm,8cm或7cm,7cm.
26.解:(1)
4个;
(2)当有n对点时,最少可以画2(n﹣1)个三角形;
(3)2×(2006﹣1)=4010个.
答:当n=2006时,最少可以画4010个三角形.
27.解:∵CD⊥AB,
∴∠CDB=90°,
∵∠B=60°,
∴∠BCD=90°﹣∠B=90°﹣60°=30°;
∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,
∴∠ACB=100°,
∵CE是∠ACB的平分线,
∴∠ACE=∠ACB=50°,
∴∠CEB=∠A+∠ACE=20°+50°=70°,
∠ECD=90°﹣70°=20°
三角形》单元测试卷
一.选择题
1.如图,共有三角形的个数是( )
A.3
B.4
C.5
D.6
2.三角形按角分类可以分为( )
A.锐角三角形、直角三角形、钝角三角形
B.等腰三角形、等边三角形、不等边三角形
C.直角三角形、等边直角三角形
D.以上答案都不正确
3.下列叙述中错误的一项是( )
A.三角形的中线、角平分线、高都是线段
B.三角形的三条高线中至少存在一条在三角形内部
C.只有一条高在三角形内部的三角形一定是钝角三角形
D.三角形的三条角平分线都在三角形内部
4.三角形的重心是( )
A.三角形三条角平分线的交点
B.三角形三条中线的交点
C.三角形三条边的垂直平分线的交点
D.三角形三条高的交点
5.下列长度的三条线段能组成三角形的是( )
A.3,4,8
B.5,6,11
C.5,6,10
D.1,2,3
6.等边三角形是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等腰直角三角形
7.如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=110°,则∠1+∠2的度数为( )
A.80°
B.90°
C.100°
D.110°
8.如图,∠A、∠1、∠2的大小关系是( )
A.∠A>∠1>∠2
B.∠2>∠1>∠A
C.∠A>∠2>∠1
D.∠2>∠A>∠1
9.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
A.两点之间线段最短
B.三角形两边之和大于第三边
C.两点确定一条直线
D.三角形的稳定性
10.如图,在△ABC中,已知点D,E,F分别是BC,AD,CE的中点,且△ABC的面积为16,则△BEF的面积是( )
A.2
B.4
C.6
D.8
二.填空题
11.BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是
.
12.如图,木工师傅做好一门框后钉上木条AB,CD,使门框不变形,这种做法依据的数学原理是
.
13.一个三角形有两边分别为4cm和8cm,则第三边长x的取值范围
.
14.如图,∠1=115°,∠2=50°,那么∠3=
.
15.如图,直角ABC的周长为2008,在其内部有五个小直角三角形,则这五个小直角三角形的周长为
.
16.三角形的三条
交于一点,这点叫做三角形的重心.
17.将一副三角板如图所示摆放(其中一块三角板的一条直角边与另一块三角板的斜边摆放在一直线上),那么图中∠α=
度.
18.如图所示,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依此类推,则第6个图中共有三角形
个.
19.图1是一个三角形,分别连接这个三角形三边的中点得到图2;再分别连接图2中间小三角形的中点,得到图3.(若三角形中含有其它三角形则不记入)
(1)图2有
个三角形;图3中有
个三角形
(2)按上面方法继续下去,第20个图有
个三角形;第n个图中有
个三角形.(用n的代数式表示结论)
20.如图,在△ABC中,点D、E、F分别是线段BC、AD、CE的中点,且S△ABC=8cm2,则S△BEF=
cm2.
三.解答题
21.如图,G为△ABC重心,已知GA=5,GB=12,GC=13,求△ABC边AB上的高.
22.一个三角形的周长为36cm,三边之比a:b:c=2:3:4,求a,b,c的值.
23.如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm.求:
(1)△ABC的面积;
(2)CD的长;
(3)作出△ABC的边AC上的中线BE,并求出△ABE的面积.
24.(1)下列图形中具有稳定性是
;(只填图形序号)
(2)对不具有稳定性的图形,请适当地添加线段,使之具有稳定性.
25.一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
26.两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为
个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2006时,按上述规则画出的图形中,最少有多少个三角形?
27.在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.
参考答案与试题解析
一.选择题
1.解:图中有:△ABC,△ABD,△ABE,△ACD,△ACE,△ADE,共6个.
故选:D.
2.解:三角形按角分类可以分为锐角三角形、直角三角形、钝角三角形,
故选:A.
3.解:A、三角形的角平分线、中线、高都是线段,故此选项正确;
B、锐角三角形的三条高都在三角形的内部;直角三角形的一条高在三角形的内部,两条就是直角边;钝角三角形的一条高在三角形的内部,两条高在三角形的外部.故此选项正确;
C、根据B中的分析,知只有一条高在三角形内部的三角形可能是直角三角形,也可能是钝角三角形.故此选项错误;
D、根据角平分线的定义,知三角形的三条角平分线都在三角形的内部.故此选项正确.
故选:C.
4.解:三角形的重心是三角形三条中线的交点.
故选:B.
5.解:3+4<8,则3,4,8不能组成三角形,A不符合题意;
5+6=11,则5,6,11不能组成三角形,B不合题意;
5+6>10,则5,6,10能组成三角形,C符合题意;
1+2=3,则1,2,3不能组成三角形,D不合题意,
故选:C.
6.解:等边三角形的三个内角都是60度,属于锐角三角形;等边三角形的三条边都相等,属于等腰三角形.观察选项,选项B符合题意.
故选:B.
7.解:连接AA′.
∵A'B平分∠ABC,A'C平分∠ACB,∠BA'C=110°,
∴∠A′BC+∠A′CB=70°,
∴∠ABC+∠ACB=140°,
∴∠BAC=180°﹣140°=40°,
∵∠1=∠DAA′+∠DA′A,∠2=∠EAA′+∠EA′A,
∵∠DAA′=∠DA′A,∠EAA′=∠EA′A,
∴∠1+∠2=2(∠DAA′+∠EAA′)=2∠BAC=80°,
故选:A.
8.解:∵∠1是三角形的一个外角,∴∠1>∠A,
又∵∠2是三角形的一个外角,∴∠2>∠1,
∴∠2>∠1>∠A.
故选:B.
9.解:根据三角形的稳定性可固定窗户.
故选:D.
10.解:如图,点F是CE的中点,
∴△BEF的底是EF,△BEC的底是EC,即EF=EC,高相等;
∴S△BEF=S△BEC,
同理得,S△DEC=S△ADC,S△DEB=S△ADB,
∴S△EBC=S△ABC,
∴S△BEF=S△ABC,且S△ABC=16,
∴S△BEF=4,
即阴影部分的面积为4.
故选:B.
二.填空题
11.解:∵BD是△ABC的中线,
∴AD=CD,
∴△ABD和△BCD的周长的差=(AB+BD+AD)﹣(BC+BD+CD)=AB﹣BC,
∵AB=5,BC=3,
∴△ABD和△BCD的周长的差=5﹣3=2.
故答案为:2.
12.解:木工师傅做好一门框后钉上木条AB,CD,使门框不变形,这种做法依据的数学原理是三角形的稳定性.
故答案为:三角形的稳定性.
13.解:∵三角形的两边的长分别为4cm和8cm,第三边的长为x,
∴根据三角形的三边关系,得:8﹣4<x<4+8,即:4cm<x<12cm.
故答案为:4cm<x<12cm.
14.解:∵∠1=115°,∠2=50°,
∴∠3=∠1﹣∠2=65°,
故答案为:65°.
15.解:∵五个小直角三角形与大三角形相似,
∴对应边的比相等,
∵五个小三角形的斜边长的和等于大三角形的斜边长,
∴五个小三角形的周长的和等于大三角形的周长为2008.
16.解:三角形的三条中线交于一点,这点叫做三角形的重心.
故答案为:中线.
17.解:∵∠1=45°,∠2=60°,
∴∠α=180°﹣45°﹣60°=75°,
故答案为75.
18.解:第n个图形中,三角形的个数是1+4(n﹣1)=4n﹣3.所以当n=6时,原式=21,
故答案为:21.
19.解:(1)图2有4个三角形;图3中有7个三角形;
(2)按上面方法继续下去,可以得到(4)比(3)增加了4个三角形,
依此类推,第20个图有3×20﹣2=58个三角形;第n个图中有(3n﹣2)个三角形.
故答案为:(1)4;7;(2)58;(3n﹣2)
20.解:∵点E是AD的中点,
∴S△ABE=S△ABD,S△ACE=S△ADC,
∴S△ABE+S△ACE=S△ABC=×8=4,
∴S△BCE=S△ABC=×8=4,
∵点F是CE的中点,
∴S△BEF=S△BCE=×4=2.
故答案为:2.
三.解答题
21.解:延长AG至E,使GD=DE,作CH⊥AB于点G.
∵G为△ABC重心,
∴AG=2GD=GE,BD=DC.
∴△BGD≌△CED(SAS).
∴∠BGE=∠GEC,EC=BG=12.
∵GC2=EG2+EC2,
∴∠BGE=∠GEC=90°.
∴S△ABD===45,
由勾股定理得
AB===13,
∴S△ABC=2S△ABD=90.
∴CH==.
22.解:设三边长分别为2x,3x,4x,
由题意得,2x+3x+4x=36,
解得:x=4.
则a=2×4=8(cm),
b=3×4=12(cm),
c=4×4=16(cm).
23.解:(1)∵∠ACB=90°,BC=12cm,AC=5cm,
∴S△ABC=BC×AC=30cm2,
(2)∵S△ABC=AB×CD=30cm2,
∴CD=30÷AB=cm,
(3)S△ABE=S△ABC=×30=15cm2
24.解:(1)具有稳定性的是①④⑥三个.
(2)如图所示:
25.解:(1)当6是腰时,底边=20﹣6×2=8cm,即其它两边是6cm,8cm,此时6+6=12,能构成三角形;
(2)当6是底边时,腰=(20﹣6)÷2=7cm,此时能构成三角形,所以其它两边是7cm、7cm.
因此其它两边长分别为7cm,7cm,
综上所述两边长分别为6cm,8cm或7cm,7cm.
26.解:(1)
4个;
(2)当有n对点时,最少可以画2(n﹣1)个三角形;
(3)2×(2006﹣1)=4010个.
答:当n=2006时,最少可以画4010个三角形.
27.解:∵CD⊥AB,
∴∠CDB=90°,
∵∠B=60°,
∴∠BCD=90°﹣∠B=90°﹣60°=30°;
∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,
∴∠ACB=100°,
∵CE是∠ACB的平分线,
∴∠ACE=∠ACB=50°,
∴∠CEB=∠A+∠ACE=20°+50°=70°,
∠ECD=90°﹣70°=20°
同课章节目录
