人教版八年级上册11.2与三角形有关的角 课时训练卷 (Word版含解析)
文档属性
| 名称 | 人教版八年级上册11.2与三角形有关的角 课时训练卷 (Word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 199.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 00:00:00 | ||
图片预览



文档简介
人教版八年级上册11.2与三角形有关的角 课时训练卷
一.选择题
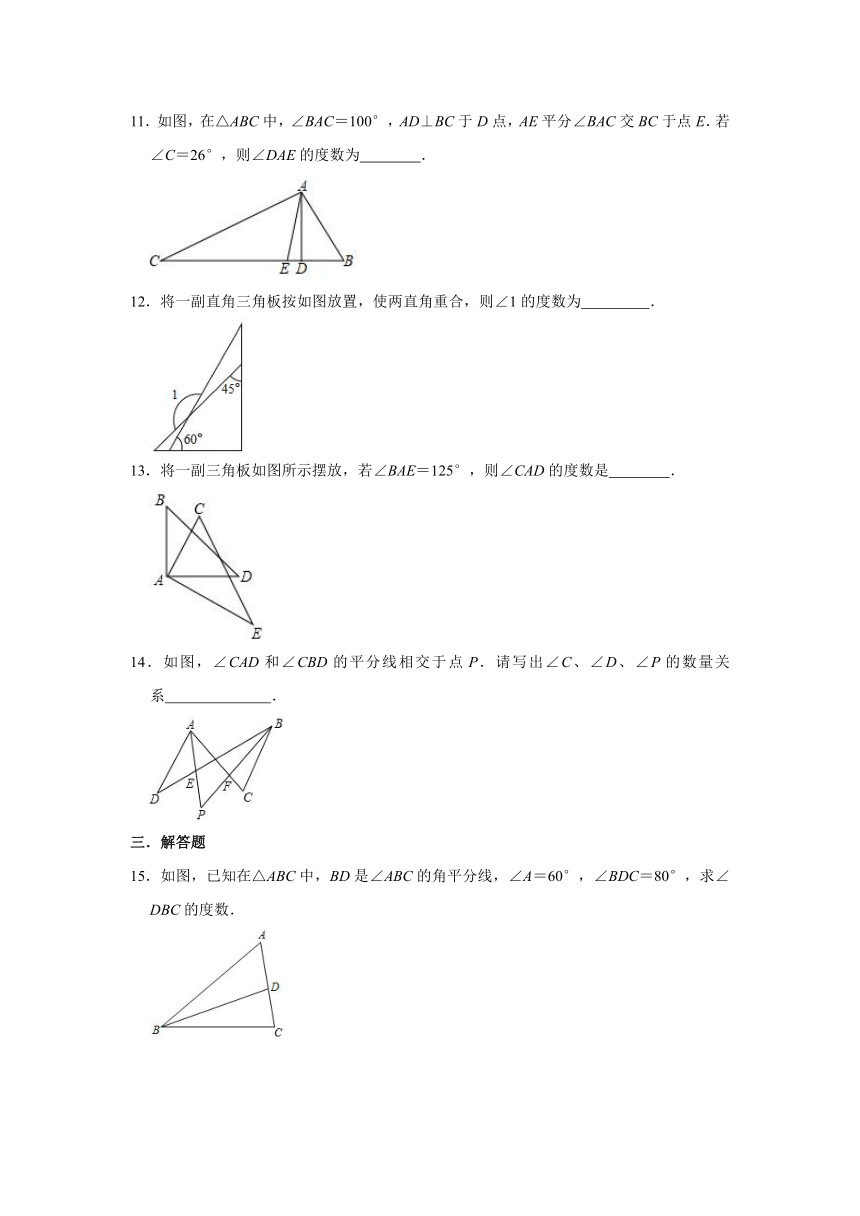
1.给定下列条件,不能判定三角形是直角三角形的是( )
A.∠A:∠B:∠C=1:2:3 B.∠A﹣∠C=∠B
C.∠A=∠B=2∠C D.∠A=∠B=∠C
2.一天,爸爸带小明到建筑工地玩,看见一个如图所示的人字架,爸爸说:“小明,我考考你,这个人字架的夹角∠1等于130°,你知道∠3比∠2大多少吗?”小明马上得到了正确的答案,他的答案是( )
A.50° B.65° C.90° D.130°
3.如果将一副三角板按如图方式叠放,那么∠1等于( )
A.120° B.105° C.60° D.45°
4.如图,在△ABC中,∠A=45°,△ABC的外角∠CBD=75°,则∠C的度数是( )
A.30° B.45° C.60° D.75°
5.如图,在△ABC中,AB=AC,∠A=40°,CD⊥AB于D,则∠DCB等于( )
A.70° B.50° C.40° D.20°
6.如图,△ABC中∠ACB=90°,且CD∥AB.∠B=60°,则∠1等于( )
A.30° B.40° C.50° D.60°
7.如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是( )
A.32° B.45° C.60° D.64°
8.如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=76°,∠C=64°,则∠DAE的度数是( )
A.10° B.12° C.15° D.18°
二.填空题
9.在直角三角形中,一个锐角为40°,那么另一个锐角为 度.
10.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,∠B=52°,那么∠ACD= .
11.如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为 .
12.将一副直角三角板按如图放置,使两直角重合,则∠1的度数为 .
13.将一副三角板如图所示摆放,若∠BAE=125°,则∠CAD的度数是 .
14.如图,∠CAD和∠CBD的平分线相交于点P.请写出∠C、∠D、∠P的数量关系 .
三.解答题
15.如图,已知在△ABC中,BD是∠ABC的角平分线,∠A=60°,∠BDC=80°,求∠DBC的度数.
16.如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,求∠CHD的度数.
17.如图,在△ABC中,BE是△ABC角平分线,点D是AB上的一点,且满足∠DEB=∠DBE.
(1)DE与BC平行吗?请说明理由;
(2)若∠C=50°,∠A=45°,求∠DEB的度数.
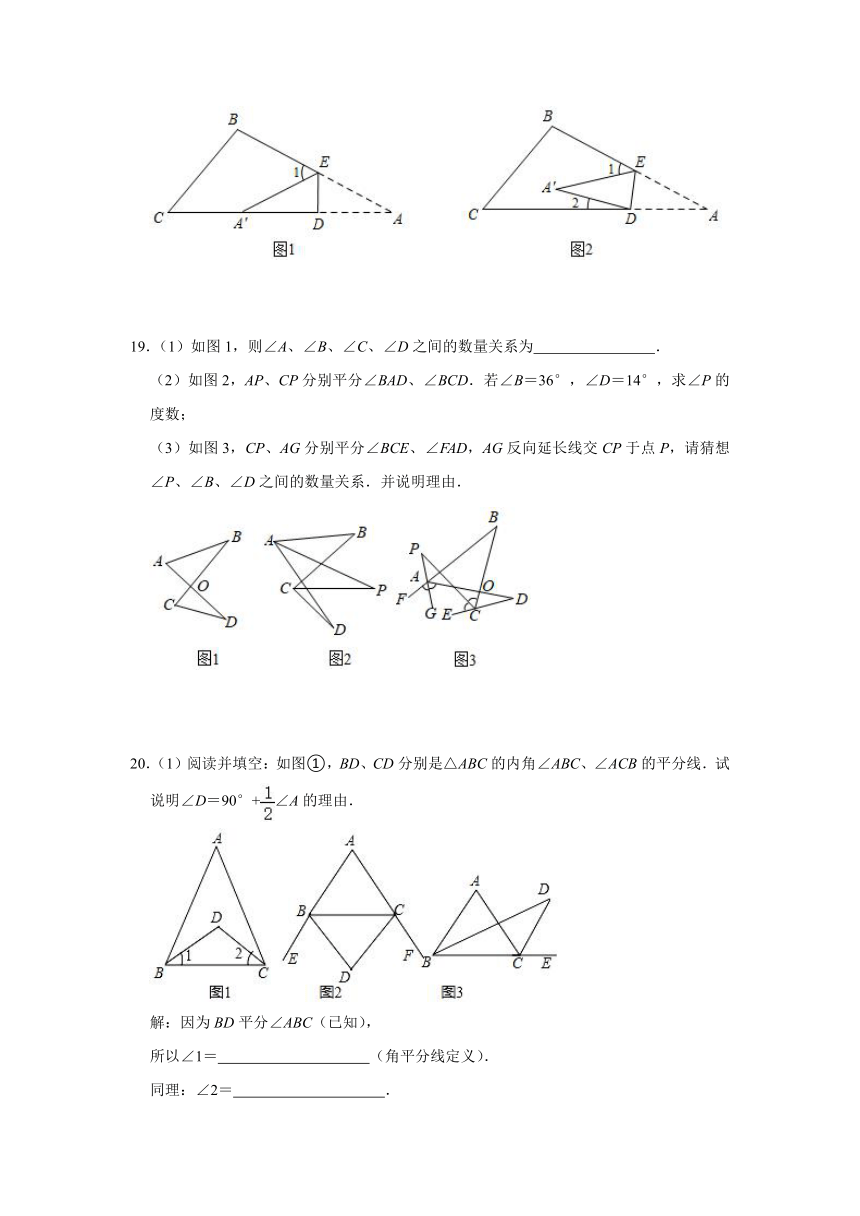
18.如图1和图2,在三角形纸片ABC中,点D,E分别在边AC,AB上,沿DE折叠,点A落在点A'的位置.
(1)如图1,当点A′落在CD边上时,∠DAE与∠1之间的数量关系为 (只填序号),并说明理由;
①∠DAE=∠1
②∠DAE=2∠1
③∠1=2∠DAE
(2)如图2,当点A落在△ABC内部时,直接写出∠DAE与∠1,∠2之间的数量关系.
19.(1)如图1,则∠A、∠B、∠C、∠D之间的数量关系为 .
(2)如图2,AP、CP分别平分∠BAD、∠BCD.若∠B=36°,∠D=14°,求∠P的度数;
(3)如图3,CP、AG分别平分∠BCE、∠FAD,AG反向延长线交CP于点P,请猜想∠P、∠B、∠D之间的数量关系.并说明理由.
20.(1)阅读并填空:如图①,BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线.试说明∠D=90°+∠A的理由.
解:因为BD平分∠ABC(已知),
所以∠1= (角平分线定义).
同理:∠2= .
因为∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°,( ),
所以∠D= (等式性质).
即:∠D=90°+∠A.
(2)探究,请直接写出结果,并任选一种情况说明理由:
(i)如图②,BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线.试探究∠D与∠A之间的等量关系.
答:∠D与∠A之间的等量关系是 .
(ii)如图③,BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线.试探究∠D与∠A之间的等量关系.
答:∠D与∠A之间的等量关系是 .
参考答案
一.选择题
1.解:A、设∠A=x,则∠B=2x,∠C=3x,
∴x+2x+3x=180°,
解得:x=30°,
∴最大角∠C=3×30°=90°,
∴三角形是直角三角形,选项A不符合题意;
B、∵∠A﹣∠C=∠B,
∴∠A=∠B+∠C,
又∵∠A+∠B+∠C=180°,
∴∠A=180°÷2=90°,
∴三角形是直角三角形,选项B不符合题意;
C、设∠C=y,则∠A=2y,∠B=2y,
∴y+2y+2y=180°,
解得:y=36°,
∴最大角∠B=2×36°=72°,
∴三角形不是直角三角形,选项C符合题意;
D、设∠A=z,则∠B=z,∠C=2z,
∴z+z+2z=180°,
解得:z=45°,
∴最大角∠C=2×45°=90°,
∴三角形是直角三角形,选项D不符合题意.
故选:C.
2.解:根据题意,∠3﹣∠2=180°﹣∠1,
且∠1=130°,
即得∠3﹣∠2=50°.
故选:A.
3.解:如图,∠2=90°﹣45°=45°,
由三角形的外角性质得,∠1=∠2+60°,
=45°+60°,
=105°.
故选:B.
4.解:∵∠A=45°,△ABC的外角∠CBD=75°,
∴∠C=∠CBD﹣∠A=75°﹣45°=30°,
故选:A.
5.解:∵AB=AC,∠A=40°,∴∠B=∠C=(180°﹣40°)÷2=70°,
又∵CD⊥AB,∴∠BDC=90°,∴∠DCB=90°﹣70°=20°.
故选:D.
6.解:∵△ABC中,∠ACB=90°,∠B=60°,
∴∠A=30°,
∵CD∥AB,
∴∠1=∠A,
∴∠1=30°,
故选:A.
7.解:如图所示:
由折叠的性质得:∠D=∠B=32°,
根据外角性质得:∠1=∠3+∠B,∠3=∠2+∠D,
∴∠1=∠2+∠D+∠B=∠2+2∠B=∠2+64°,
∴∠1﹣∠2=64°.
故选:D.
8.解:∵AE平分∠BAC,
∴∠CAE=∠CAB=×76°=38°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=90°﹣∠C=90°﹣64°=26°,
∴∠DAE=∠EAC﹣∠CAD=38°﹣26°=12°,
故选:B.
二.填空题
9.解:∵直角三角形的一个锐角为40°,
∴另一个锐角为90°﹣40°=50°,
故答案为:50.
10.解:∵∠ACB=90°,
∴∠B+∠A=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠ACD=∠B,
∵∠B=52°,
∴∠ACD=52°,
故答案为:52°.
11.解:∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=180°﹣∠ADC﹣∠C=180°﹣90°﹣26°=64°,
∵AE平分∠BAC,
∴∠CAE=∠BAC=×100°=50°,
∴∠DAE=∠CAD﹣∠CAE=64°﹣50°=14°.
故答案为14°.
12.解:如图,由题意知,∠CAD=60°,∠B=90°﹣45°=45°,
∴∠CAB=120°,
∴∠1=∠B+∠CAB=45°+120°=165°.
故答案为:165°.
13.解:∵∠BAE=125°,
∴∠DAE=∠BAE﹣∠BAD=125°﹣90°=35°,
∴∠CAD=∠CAE﹣∠DAE=90°﹣35°=55°,
故答案为:55°.
14.解:∵∠BFA=∠PAC+∠P,∠BFA=∠PBC+∠C,
∴∠PAC+∠P=∠PBC+∠C,
∵∠CAD和∠CBD的平分线相交于点P,
∴∠PAC=∠CAD,∠PBC=∠CBD,
∴∠CAD+∠P=∠CBD+∠C①,
同理:∠CAD+∠D=∠CBD+∠P②,
①﹣②,得∠P﹣∠D=∠C﹣∠P,
整理得,2∠P=∠D+∠C,
故答案为:2∠P=∠D+∠C.
三.解答题
15.解:∵∠A=60°,∠BDC=80°,
∴∠ABD=∠BDC﹣∠A=80°﹣60°=20°.
又∵BD是∠ABC的角平分线,
∴∠DBC=∠ABD=20°.
16.解:延长CH交AB于F,
在△ABC中,三边的高交于一点,所以CF⊥AB,
∵∠BAC=75°,且CF⊥AB,∴∠ACF=15°,
∵∠ACB=60°,∴∠BCF=45°
在△CDH中,三内角之和为180°,
∴∠CHD=45°,
17.解:(1)DE∥BC.
理由如下:∵BE是△ABC的角平分线,
∴∠DBE=∠EBC,
∵∠DEB=∠DBE,
∴∠DEB=∠EBC,
∴DE∥BC;
(2)在△ABC中,∠A+∠ABC+∠C=180°,
∴∠ABC=180°﹣∠A﹣∠C=180°﹣45°﹣50°=85°.
∵BE是△ABC的角平分线,
∴∠DBE=∠EBC=42.5°,
∴∠DEB=∠EBC=42.5°.
18.解:(1)由题意得:∠DAE=∠DA′E.
∵∠1=∠EAD+∠EA′D=2∠DAE.
故答案为:③.
(2)∠1+∠2=2∠DAE,理由如下:
如图2,连接AA′.
由题意知:∠EAD=∠EA′D.
∵∠1=∠A′AE+∠AA′E,∠2=∠A′AD+∠AA′D,
∴∠1+∠2=∠EAA′+∠A′AD+∠EA′A+∠AA′D=∠EAD+∠EA′D=2∠EAD.
19.解:(1)∵∠AOB+∠A+∠B=∠COD+∠C+∠D=180°,∠AOB=∠COD,
∴∠A+∠B=∠C+∠D,
故答案为∠A+∠B=∠C+∠D;
(2)∵AP、CP分别平分∠BAD、∠BCD,
∴∠BAP=∠DAP,∠BCP=∠DCP,
由(1)可得:∠BAP+∠B=∠BCP+∠P,∠DAP+∠P=∠DCP+∠D,
∴∠B﹣∠P=∠P﹣∠D,
即2∠P=∠B+∠D,
∵∠B=36°,∠D=14°,
∴∠P=25°;
(3)2∠P=∠B+∠D.
理由:∵CP、AG分别平分∠BCE、∠FAD,
∴∠ECP=∠PCB,∠FAG=∠GAD,
∵∠PAB=∠FAG,
∴∠GAD=∠PAB,
∵∠P+∠PAB=∠B+∠PCB,
∴∠P+∠GAD=∠B+∠PCB,
∵∠P+∠PAD=∠D+∠PCD,
∴∠P+(180°﹣∠GAD)=∠D+(180°﹣∠ECP),
∴2∠P=∠B+∠D.
20.解:(1)解:因为BD平分∠ABC(已知),
所以∠1=∠ABC (角平分线定义).
同理:∠2=∠ACB.
因为∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°,( 三角形的内角和等于180° ),
所以∠D=180°﹣(∠ABC+∠ACB) (等式性质).
即:∠D=90°+∠A.
故答案为:ABC,ACB,三角形的内角和等于180°,180°﹣(∠ABC+∠ACB).
(2)解:(i)∠D与∠A之间的等量关系是:∠D=90°﹣∠A.
理由:∵BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,
∴∠EBD=∠DBC,∠BCD=∠DCF,
∴∠DBC+∠DCB+∠D=180°,
∴∠A+∠ABC+∠ACB=180°,
而∠ABC=180°﹣2∠DBC,
∠ACB=180°﹣2∠DCB,
∴∠A+180°﹣2∠DBC+180°﹣2∠DCB=180°,
∴∠A﹣2(∠DBC+∠DCB)=﹣180°,
∴∠A﹣2(180°﹣∠D)=﹣180°,
∴∠A+2∠D=180°,
∴∠D=90°﹣∠A,
故答案为:∠D=90°﹣∠A;
(ii)∠D与∠A之间的等量关系是:∠D=∠A.
理由:∵BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,
∴∠DCE=∠DBC+∠D,
∵∠A+2∠DBC=2∠DCE
∴∠A+2∠DBC=2∠DBC+2∠D
∴∠A=2∠D
即:∠D=∠A.
故答案为:∠D=∠A.
一.选择题
1.给定下列条件,不能判定三角形是直角三角形的是( )
A.∠A:∠B:∠C=1:2:3 B.∠A﹣∠C=∠B
C.∠A=∠B=2∠C D.∠A=∠B=∠C
2.一天,爸爸带小明到建筑工地玩,看见一个如图所示的人字架,爸爸说:“小明,我考考你,这个人字架的夹角∠1等于130°,你知道∠3比∠2大多少吗?”小明马上得到了正确的答案,他的答案是( )
A.50° B.65° C.90° D.130°
3.如果将一副三角板按如图方式叠放,那么∠1等于( )
A.120° B.105° C.60° D.45°
4.如图,在△ABC中,∠A=45°,△ABC的外角∠CBD=75°,则∠C的度数是( )
A.30° B.45° C.60° D.75°
5.如图,在△ABC中,AB=AC,∠A=40°,CD⊥AB于D,则∠DCB等于( )
A.70° B.50° C.40° D.20°
6.如图,△ABC中∠ACB=90°,且CD∥AB.∠B=60°,则∠1等于( )
A.30° B.40° C.50° D.60°
7.如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是( )
A.32° B.45° C.60° D.64°
8.如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=76°,∠C=64°,则∠DAE的度数是( )
A.10° B.12° C.15° D.18°
二.填空题
9.在直角三角形中,一个锐角为40°,那么另一个锐角为 度.
10.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,∠B=52°,那么∠ACD= .
11.如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为 .
12.将一副直角三角板按如图放置,使两直角重合,则∠1的度数为 .
13.将一副三角板如图所示摆放,若∠BAE=125°,则∠CAD的度数是 .
14.如图,∠CAD和∠CBD的平分线相交于点P.请写出∠C、∠D、∠P的数量关系 .
三.解答题
15.如图,已知在△ABC中,BD是∠ABC的角平分线,∠A=60°,∠BDC=80°,求∠DBC的度数.
16.如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,求∠CHD的度数.
17.如图,在△ABC中,BE是△ABC角平分线,点D是AB上的一点,且满足∠DEB=∠DBE.
(1)DE与BC平行吗?请说明理由;
(2)若∠C=50°,∠A=45°,求∠DEB的度数.
18.如图1和图2,在三角形纸片ABC中,点D,E分别在边AC,AB上,沿DE折叠,点A落在点A'的位置.
(1)如图1,当点A′落在CD边上时,∠DAE与∠1之间的数量关系为 (只填序号),并说明理由;
①∠DAE=∠1
②∠DAE=2∠1
③∠1=2∠DAE
(2)如图2,当点A落在△ABC内部时,直接写出∠DAE与∠1,∠2之间的数量关系.
19.(1)如图1,则∠A、∠B、∠C、∠D之间的数量关系为 .
(2)如图2,AP、CP分别平分∠BAD、∠BCD.若∠B=36°,∠D=14°,求∠P的度数;
(3)如图3,CP、AG分别平分∠BCE、∠FAD,AG反向延长线交CP于点P,请猜想∠P、∠B、∠D之间的数量关系.并说明理由.
20.(1)阅读并填空:如图①,BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线.试说明∠D=90°+∠A的理由.
解:因为BD平分∠ABC(已知),
所以∠1= (角平分线定义).
同理:∠2= .
因为∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°,( ),
所以∠D= (等式性质).
即:∠D=90°+∠A.
(2)探究,请直接写出结果,并任选一种情况说明理由:
(i)如图②,BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线.试探究∠D与∠A之间的等量关系.
答:∠D与∠A之间的等量关系是 .
(ii)如图③,BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线.试探究∠D与∠A之间的等量关系.
答:∠D与∠A之间的等量关系是 .
参考答案
一.选择题
1.解:A、设∠A=x,则∠B=2x,∠C=3x,
∴x+2x+3x=180°,
解得:x=30°,
∴最大角∠C=3×30°=90°,
∴三角形是直角三角形,选项A不符合题意;
B、∵∠A﹣∠C=∠B,
∴∠A=∠B+∠C,
又∵∠A+∠B+∠C=180°,
∴∠A=180°÷2=90°,
∴三角形是直角三角形,选项B不符合题意;
C、设∠C=y,则∠A=2y,∠B=2y,
∴y+2y+2y=180°,
解得:y=36°,
∴最大角∠B=2×36°=72°,
∴三角形不是直角三角形,选项C符合题意;
D、设∠A=z,则∠B=z,∠C=2z,
∴z+z+2z=180°,
解得:z=45°,
∴最大角∠C=2×45°=90°,
∴三角形是直角三角形,选项D不符合题意.
故选:C.
2.解:根据题意,∠3﹣∠2=180°﹣∠1,
且∠1=130°,
即得∠3﹣∠2=50°.
故选:A.
3.解:如图,∠2=90°﹣45°=45°,
由三角形的外角性质得,∠1=∠2+60°,
=45°+60°,
=105°.
故选:B.
4.解:∵∠A=45°,△ABC的外角∠CBD=75°,
∴∠C=∠CBD﹣∠A=75°﹣45°=30°,
故选:A.
5.解:∵AB=AC,∠A=40°,∴∠B=∠C=(180°﹣40°)÷2=70°,
又∵CD⊥AB,∴∠BDC=90°,∴∠DCB=90°﹣70°=20°.
故选:D.
6.解:∵△ABC中,∠ACB=90°,∠B=60°,
∴∠A=30°,
∵CD∥AB,
∴∠1=∠A,
∴∠1=30°,
故选:A.
7.解:如图所示:
由折叠的性质得:∠D=∠B=32°,
根据外角性质得:∠1=∠3+∠B,∠3=∠2+∠D,
∴∠1=∠2+∠D+∠B=∠2+2∠B=∠2+64°,
∴∠1﹣∠2=64°.
故选:D.
8.解:∵AE平分∠BAC,
∴∠CAE=∠CAB=×76°=38°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=90°﹣∠C=90°﹣64°=26°,
∴∠DAE=∠EAC﹣∠CAD=38°﹣26°=12°,
故选:B.
二.填空题
9.解:∵直角三角形的一个锐角为40°,
∴另一个锐角为90°﹣40°=50°,
故答案为:50.
10.解:∵∠ACB=90°,
∴∠B+∠A=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠ACD=∠B,
∵∠B=52°,
∴∠ACD=52°,
故答案为:52°.
11.解:∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=180°﹣∠ADC﹣∠C=180°﹣90°﹣26°=64°,
∵AE平分∠BAC,
∴∠CAE=∠BAC=×100°=50°,
∴∠DAE=∠CAD﹣∠CAE=64°﹣50°=14°.
故答案为14°.
12.解:如图,由题意知,∠CAD=60°,∠B=90°﹣45°=45°,
∴∠CAB=120°,
∴∠1=∠B+∠CAB=45°+120°=165°.
故答案为:165°.
13.解:∵∠BAE=125°,
∴∠DAE=∠BAE﹣∠BAD=125°﹣90°=35°,
∴∠CAD=∠CAE﹣∠DAE=90°﹣35°=55°,
故答案为:55°.
14.解:∵∠BFA=∠PAC+∠P,∠BFA=∠PBC+∠C,
∴∠PAC+∠P=∠PBC+∠C,
∵∠CAD和∠CBD的平分线相交于点P,
∴∠PAC=∠CAD,∠PBC=∠CBD,
∴∠CAD+∠P=∠CBD+∠C①,
同理:∠CAD+∠D=∠CBD+∠P②,
①﹣②,得∠P﹣∠D=∠C﹣∠P,
整理得,2∠P=∠D+∠C,
故答案为:2∠P=∠D+∠C.
三.解答题
15.解:∵∠A=60°,∠BDC=80°,
∴∠ABD=∠BDC﹣∠A=80°﹣60°=20°.
又∵BD是∠ABC的角平分线,
∴∠DBC=∠ABD=20°.
16.解:延长CH交AB于F,
在△ABC中,三边的高交于一点,所以CF⊥AB,
∵∠BAC=75°,且CF⊥AB,∴∠ACF=15°,
∵∠ACB=60°,∴∠BCF=45°
在△CDH中,三内角之和为180°,
∴∠CHD=45°,
17.解:(1)DE∥BC.
理由如下:∵BE是△ABC的角平分线,
∴∠DBE=∠EBC,
∵∠DEB=∠DBE,
∴∠DEB=∠EBC,
∴DE∥BC;
(2)在△ABC中,∠A+∠ABC+∠C=180°,
∴∠ABC=180°﹣∠A﹣∠C=180°﹣45°﹣50°=85°.
∵BE是△ABC的角平分线,
∴∠DBE=∠EBC=42.5°,
∴∠DEB=∠EBC=42.5°.
18.解:(1)由题意得:∠DAE=∠DA′E.
∵∠1=∠EAD+∠EA′D=2∠DAE.
故答案为:③.
(2)∠1+∠2=2∠DAE,理由如下:
如图2,连接AA′.
由题意知:∠EAD=∠EA′D.
∵∠1=∠A′AE+∠AA′E,∠2=∠A′AD+∠AA′D,
∴∠1+∠2=∠EAA′+∠A′AD+∠EA′A+∠AA′D=∠EAD+∠EA′D=2∠EAD.
19.解:(1)∵∠AOB+∠A+∠B=∠COD+∠C+∠D=180°,∠AOB=∠COD,
∴∠A+∠B=∠C+∠D,
故答案为∠A+∠B=∠C+∠D;
(2)∵AP、CP分别平分∠BAD、∠BCD,
∴∠BAP=∠DAP,∠BCP=∠DCP,
由(1)可得:∠BAP+∠B=∠BCP+∠P,∠DAP+∠P=∠DCP+∠D,
∴∠B﹣∠P=∠P﹣∠D,
即2∠P=∠B+∠D,
∵∠B=36°,∠D=14°,
∴∠P=25°;
(3)2∠P=∠B+∠D.
理由:∵CP、AG分别平分∠BCE、∠FAD,
∴∠ECP=∠PCB,∠FAG=∠GAD,
∵∠PAB=∠FAG,
∴∠GAD=∠PAB,
∵∠P+∠PAB=∠B+∠PCB,
∴∠P+∠GAD=∠B+∠PCB,
∵∠P+∠PAD=∠D+∠PCD,
∴∠P+(180°﹣∠GAD)=∠D+(180°﹣∠ECP),
∴2∠P=∠B+∠D.
20.解:(1)解:因为BD平分∠ABC(已知),
所以∠1=∠ABC (角平分线定义).
同理:∠2=∠ACB.
因为∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°,( 三角形的内角和等于180° ),
所以∠D=180°﹣(∠ABC+∠ACB) (等式性质).
即:∠D=90°+∠A.
故答案为:ABC,ACB,三角形的内角和等于180°,180°﹣(∠ABC+∠ACB).
(2)解:(i)∠D与∠A之间的等量关系是:∠D=90°﹣∠A.
理由:∵BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,
∴∠EBD=∠DBC,∠BCD=∠DCF,
∴∠DBC+∠DCB+∠D=180°,
∴∠A+∠ABC+∠ACB=180°,
而∠ABC=180°﹣2∠DBC,
∠ACB=180°﹣2∠DCB,
∴∠A+180°﹣2∠DBC+180°﹣2∠DCB=180°,
∴∠A﹣2(∠DBC+∠DCB)=﹣180°,
∴∠A﹣2(180°﹣∠D)=﹣180°,
∴∠A+2∠D=180°,
∴∠D=90°﹣∠A,
故答案为:∠D=90°﹣∠A;
(ii)∠D与∠A之间的等量关系是:∠D=∠A.
理由:∵BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,
∴∠DCE=∠DBC+∠D,
∵∠A+2∠DBC=2∠DCE
∴∠A+2∠DBC=2∠DBC+2∠D
∴∠A=2∠D
即:∠D=∠A.
故答案为:∠D=∠A.
